-
Esta questão é simples!
Já que no enunciado diz que todas as mulheres devem ficar sentadas, então calcularemos apenas o que restão para os homens.
8!/5! 3!=
336/6=56 são as maneiras distintas que podem ocupar as 13 cadeiras!
-
São 16 pessoas. 8 homens e 8 mulheres.
Para às 16 pessoas existem apenas 13 cadeiras.
Todas as mulheres devem ficar sentadas.
M.M.M.M.M.M.M.M.H.H.H.H.H.
Portanto das 8 mulheres 8 sentarão, não importando a ordem pois todas sentaram.
então Combinação C 8/8= 1
Dos 8 homens apenas 5 sentaram. Mais quais dos 5? Tanto faz. Apenas queremos 5 homens sentados.
então combinação C 8/5= 8x7x6x5x4 / 5x4x3x2x1 = 6 720 / 120 = 56.
-
O meu também.
-
Como todas as mulheres sempre deverão ficar sentadas, de um total de
13 cadeiras, restarão para os homens sentarem apenas 5 cadeiras. Como
temos 8 homens, vamos fazer uma combinação tomando de 8 a 13.
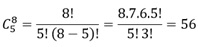
Letra A.
-
Se todas as mulheres expressamente têm de ficarem sentadas, então precisamos apenas contar as possiblidades dos homens que serão 5 dentre os 8.
Portanto, 8.7.6.5.4/5!
56 maneiras.
-
que questão fácil , fiz o pior caminho pra nada
-
Essa banca adora confundir, por exemplo:
"sendo que em nenhuma vez fique uma mulher em pé?"
Com isso induz o candidato a pensar que apenas 1 mulher não pode ficar de pé, más que 2 ou 3 podem.
Deveriam escrever assim:
"sendo que em nenhuma vez fique QUALQUER mulher em pé?"
-
Alana, não pode ser por permutação, pois permutação é um tipo de arranjo, e a questão é de combinação!
entendeu?
Bons estudos!!
-
Eu faria por permutação.. daria um número gigante! Não entendi ainda como a ordem não importa!
-
O exercicio não diz que existe diferença na ordem das pessoas sentadas, portanto Fulano sentado = Sicrano sentado, ou seja ,apenas precisamos diferenciar se a pessoa está sentada ou não.
Foi dito que sempre as mulheres estarão sentadas, sendo portando apenas 1 possibilidade. Entre os 8 homens restaram as 5 cadeiras, logo um combinação: C (8,5) = C (8,3) = 8*7*6 / 3*2*1 = 56
Possibilidades das mulheres = 1
Possibilidades dos homens = 56
Possibilidade da combinação: 1 * 56 = 56
-
A pergunta quer saber quem vai ficar em pé, lembrando que todas as mulheres vão ficar sentadas. Logo você vai tirar 5 lugares de 8 homens.
Pra saber quem vai ficar em pé e contagem...
C8/3...Porque os números são de homens e de quantos vão ficar em pé.
C= 8.7.6/3.2.1->simplifica 6 pelo 3 e 2 de baixo, sobrando 8 e 7 que se multiplicam dando 56.
Espero ter explicado para todos entenderem.
-
Alternativa A.
Das 13 cadeiras, 8 estarão ocupadas pelas mulheres. Então resta fazer a Combinação (sem ordem) dos 8 homens pelas 5 cadeiras restantes.
Para diminuir o cálculo, uso a combinação complementar --> 8-5 = 3
C(8,5) = C(8,3) = 8.7.6 / 3.2.1 = 56
-
Enunciado dá a entender que a ordem importa.
-
A ordem não importa...
-
Tenho 8 HOMENS e 8 MULHERES PARA 13 CADEIRAS.
Bizu: As mulheres não podem ficar em pé! Logo.... só restam 5 cadeiras para os homens!
Então fica assim: Não interessa a ordem! Independente de onde as mulheres vão sentar, só restará 5 cadeiras para os homens!!
8 x 7 x 6 x 5 x 4
_______________________________________________________= 56
5x4x3x2
-
Na minha opinião, para que se configure formas distintas, as mulheres ,nas 8 cadeiras, deveriam mudar de lugar.
Se a ordem não importasse elas poderiam se sentar nas mesmas cadeiras alterando apenas os homens que se sentariam.
Acho que ficou faltando esse detalhe.
-
Lendo o enunciado,parece que a ordem importa. Mal feita .
-
TÃO DIFÍCIL PRA MIM, JESUS!!!!!!
SOU UMA ANTA
-
Sempre que for fazer esse tipo de questão desenhe primeiro, para ter uma visão melhor do problema.
os oitos lugares das mulheres já estão garantidos, sobrando assim somente 5 lugares para os homens se sentarem.
|H|H|H|H|H|M|M|M|M|M|M|M|M|
sendo assim, como a ordem da posição dos homens não importa, faz-se por combinação:
C 8,5 = 56
gab. A
-
Alguém poderia me enviar o por quê de não ser necessário fazer uma permutação entre as mulheres? Pois se todas vão sentar, também há a possibilidade delas trocarem de lugar entre elas, não?!
Obrigada!
-
8/1*7/2*6/3*5/4*4/5*3/6*2/7*1/8*8/1*7/2*6/3*5/4*4/5 - Ai vc corta os números q são iguais, os que estão em negrito respectivamente. Dessa forma, sobrando:8/1*7/2*6/3=56 e gerando o resultado correto.
@André Ricardo, no anunciado da questão deixa claro a pergunta de quantas maneiras DISTINTAS as 16 pessoas podem ocupar a cadeira SENDO TODAS AS MULHERES SENTADAS, ou seja não importa se a mulher está sentada na primeira, segunda ou as seguintes contanto que nenhumas esteja em pé.
Espero ter ajudado, att(...)
-
PM/PA
Mal elaborada, se for de maneiras distintas, entende-se que as mulheres podem também mudar de lugar, pois o único requisito é elas estarem sentadas.
Mas não devemos brigar com a banca durante a prova, queremos é a vaga. Depois brigamos kkk
Combinação se oito vagas já estão ocupadas pelas mulheres, sobram 5 lugares para escolher entre os oito homens.
escolher sem restrições passa ideia de combinação
C8,5 = 56
#FÉ NO PAI