-
C*( 1 + 0,05 )^2 = 10500*( 1 + 0,05 ) + 11025 C*( 1,05 )^2 = 22050 1,1025C =22050C=22.050/1,1025C C=20000 Alternativa E
-
A lógica abaixo é a mais simples possível:1) aplico o capital inicial a 5%am2) após um mês retiro 10.500 do saldo devedor do referido mês3) o saldo remanescente é aplicado novamente a 5% am4) no próximo mês teremos 11.025(C x 1,05 - 10.500) x 1,05 = 11.025C = 20.000Bons estudos.
-
Vamos lá..
10.500 / 1,05 = 10.000
11025 / (1,05)² = 11.025 / 1,1025 = 10.000
VI = 10.000 + 10.000 = 20.000
-
ex: depósito 01/03
01/03 C
01/04 1,05C - 10500
01/05 1,1025C - 11025
Então faz
1,1025C - 11025 = 11025 ( valor que tinha na conta nessa data e foi todo retirado)
1,1025C = 22050
C = 20000
Para isso fiz os seguintes cálculos de juros compostos:
M = C(1+I)^t
M = C(1+0,05) = 1,05C
e...
M= (1,05C - 10500) (1.05) = 1,1025C-11025
-
Aplicando
a fórmula de juros compostos:
M = P . (1 + i)n
1°
retirada:
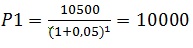
2°
retirada:
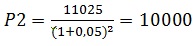
Logo, o
Valor investido será: Vinv = P1 + P2 = 20.000,00
Letra E.
-
Vou ser rapido e claro. nao eh necessario fazer nenhum calculo extenso. voce soh terah que descapitalizar pelo periodo. temos que a taxa eh 5%. Entao o montante eh = 100%+5%? correto? que eh igual 1,05. se no primeiro periodo ele tirou 10500, descapitalizando temos 10000. (o que nem precisa de calculo) e o valor de r$ 11025 que eh refente ao segundo periodo eh soh descapitalizar por 1,05*1,05= 1,1025, ficando mais que obvio que o valor presente eh tb r$ 10.000. Entao 10.000 +10.000= 20.000 resposta eh a letra e. dfesculpem a grafia estou escrevendo do celular.
-
Valor do depósito = x
1 mês depois = x + 0,05 x -10500, supondo y = x + 0,05 x -10500
2 meses depois = y + 0,05 y - 11025 = 0
y + 0,05 y - 11025 = 0
1,05 y = 11025
y = 10500
Substituindo:
y = x + 0,05 x -10500
10500 = x + 0,05 x -10500
21000 = 1,05 x
x = 20000
Resposta = E.
-
resolvi igual ao último
-
Basta descapitalizar.
1º depósito: 10.500 / 1,05 = 10.000
2º depósito: 11.025 / 1,1025 = 10.000
VPL = 10.000 + 10.000 = 20.000 ( alternativa E)
-
Observe que o investidor efetua um desembolso (investimento), na data inicial t = 0, de valor desconhecido, e depois tem dois recebimentos nas datas t = 1 mês e t = 2 meses. A taxa interna de retorno é j = 5%. Chamando de X o valor do Investimento inicial, o VPL deste fluxo de caixa é:

Como estamos usando a taxa interna de retorno, já sabemos quanto deve dar o VPL: ZERO! Assim,

Resposta: E