-
O volume é diretamente proporcional à
altura e também diretamente proporcional ao quadrado do diâmetro da lata ;Logo V = h * d²
A quantidade de material gasta para fabricar a superfície
lateral é diretamente proporcional à altura e também diretamente proporcional
ao diâmetro da lata; Logo, m = h * d
O volume da lata tipo I é o dobro do volume da lata tipo II,
logo V1 = 2 V2
V1 = 2 V2
h1 * d1²= 2 h2 * d2²
(A)
A quantidade de material gasta para
fabricar a superfície lateral dos dois tipos de latas é igual
m1 = m2
h1 * d1 = h2 * d2 (B)
Substituindo (B) em (A), temos
h1 * d1² = 2 h2 * d2²
h2 * d2 * d1 = 2 h2 * d2²
(simplificando)
d1 = 2 * d2 (o diâmetro da lata tipo I é o dobro do diâmetro da lata tipo
II)
Substituindo em (B)
h1 * d1 = h2 * d2
h1 * 2 * d2 = h2 * d2
(simplificando)
h1 * 2= h2
h1 = h2
/2 A altura da lata tipo I é igual à metade da altura da
lata tipo II
Gabarito: D
-
Resolvi mais rápido chutando valores para as duas equações seguintes. Sendo a área lateral igual, temos que 2 pi r . h = 2 pi R . H e sendo que o volume de I é o dobro do volume de II, então: pi. R² . H = 2 pi. r² . h Usando R = 10, H = 1 e r =5, h =2 temos a solução.
-
Alguém pode dar uma explicação mais didática por favor? Que simplificação foi essa de B em A?
-
Tiago, a Érica já adiantou a divisão que vinha em seguida, vou fazer passo a passo, bem explicadinho:
(h= altura, v= volume, d= diâmetro)
A gente parte dos conceitos dados, que em expressões numéricas seriam isso: V = h * d² M = h * d
Aplicando à questão temos:V1 = 2V2 M1 = M2
h1 * d1² = 2 * h2 * d2² (A) h1 * d1 = h2 * d2 (B)
São expressões com duas incógnitas (h e d), pra saber a relação entre h1 e h2 temos que isolá-los em uma expressão. Para isso, primeiros vamos isolar o "d". h1 = (h2 * d2 / d1)
(B)(h2 * d2 / d1) * d1² = 2 * h2 * d2² (A)
h2 * d2 * d1² / d1 = 2 * h2 * d2² ----------> dividimos d1² por d1
h2 * d2 * d1 = 2 * h2 * d2² -------------------> cortamos os valores equivalentes (como só tem multiplicações, podemos fazer isso)
d1 = 2 * d2
h1 * d1 = h2 * d2
(B)h1 * 2 * d2 = h2 * d2 -------------------> cortamos os valores equivalentes (como só tem multiplicações, podemos fazer isso)
h1 * 2 = h2
h1 = h2/2
-
Como a lata I pode ter duas vezes o volume da lata II e ao mesmo tempo ser menor (altura) e gastar a mesmo material superficial?!
-
Chamando de V1, A1, D1 e Q1 o volume, altura, diâmetro e quantidade de material da primeira lata, respectivamente, e de V2, A2, D2 e Q2 o volume, altura, diâmetro e quantidade de material da segunda lata, temos o seguinte:
V1 = 2V2, uma vez que o volume da primeira lata é o dobro do volume da segunda lata.
Q1 = Q2, pois a quantidade de material gasta para fabricar a superfície lateral de cada uma das latas é igual
O enunciado nos informou que o volume é diretamente proporcional à altura e também ao quadrado do diâmetro da lata. Ou seja:
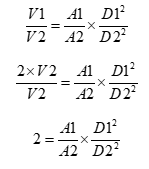
O enunciado também informou que a quantidade de material é diretamente proporcional à altura e também diretamente proporcional ao diâmetro:



A expressão acima nos mostra que a altura da lata I é igual à metade da altura da lata II.
-
??????
-
Montar a expressão já é um desafio. Resolve-la é estar um degrau acima...tentei, mas desta vez não deu