-
Para resolver essa questão não precisa usar o prazo informado, 6 meses. Isso porque pede-se a taxa no período, e não a taxa mensal. O juros real é igual à taxa nominal menos a inflação.
Um jeito rápido de resolver é calcular quando do acréscimo de R$ 382,00 pode ser creditado à inflação do período. Se a taxa de inflação foi de 3,5% multiplica-se 5.000 por 1,035, obtendo 5.175. Então pode-se concluir que dos R$ 382,00 acrescidos ao montante nos 6 meses, R$ 175,00 foi devido à inflação.
Depois vemos qual foi o acréscimo real do montante, devido aos juros reais. Para isso subtrai-se os 175 dos 382, resultando em 207. Significa que do total de R$ 382,00, apenas R$ 207,00 deve-se à taxa de juros real.
Agora com uma regra de três fica fácil achar a taxa real.
5.000 ---- 100
5.207 ---- x
x = 520700/5000 = 104,14. Ou seja, a taxa de juros real foi de 4,14% e seu valor mais próximo informado é o da alternativa B, 4%.
-
Usando a formula do montante, M=C(1+i)^n , chegaremos a taxa aparente de 0,0764, dai é só substituir na fórmula: (1+A)=(1+R)(1+I)
==>1,076=(1+R)x1,035 ==>1+R=1,04 ==> R = 4%
-
Jeito fácil:
5.382/5000= 1,08 --> 1,08*((1-(3,5/100))= 1,08*0,97= 1,04--> (1,04-1)*100= 4%
-
Vamos lá..
1° Saber a taxa.
5.382 = 5.000 . F
F = 1.0764
ou seja taxa de 7.64%
2° Descontar a inflação.
I = 1.0764 / 1.035
I = 1.04 ou seja 4%
Alternativa B
-
6 meses = 1 semestre
5.382 = 5000 (1 + i)¹
1,0764 = 1 + i
i = 0,0764
Ireal = I nominal / I inflação
I = 1,0764 / 1,035
I = 1,04
-
Esta questão como todas na Matemática em geral pode ser resolvida de varias maneiras.
Mas como estamos em luta contra o tempo numa prova de concurso então devemos realizar esta e outras questões da forma mais ágil e simples possivel.
Creio ser esta a forma mais fácil e rápida para responder esta questão. Princinpalmente para quem não sabe a formula do Montante M=C.(1+i)t etc.
Primeiro faça uma regra de três simples:
5000 ---> 100
382 ---> x
Meio pelos extremos temos:
x= 38200 x = 7,64% Esta é a taxa Nominal.
5000
Como a questão pede a Taxa Real ou Efetiva basta apenas subtrair, desta forma, o valor da inflação do valor nominal corresponde ao periodo. Desta forma:
Te=Tn-Ip onde Te = Taxa Efetiva ou Real,
Tn = Taxa Nominal,
Ip = inflação do periodo
Substituindo: Te = 7,64 - 3,50 = 4,14% é o valor aproximado Resposta auternativa B
Espero ter ajudado Bons estudos e MUITO SUCESSO em sua carreira pública!
-
C =
5.000,00
M =
5.382,00
n = 1
semestre (6 meses = 1 semestre)
i = 3,5% a.s
Utilizando
a fórmula do montante, M = c. (1+i)n e substituindo os valores na mesma:
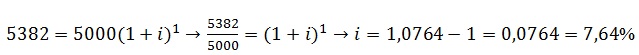
Logo
acabamos de encontrar a taxa nominal. Assim: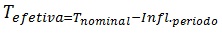
Tefetiva = 7,64 - 3,50 = 4,14 ≅ 4%
Letra B.
-
Pessoal este negocio de subtrair para encontrar a taxa real esta errado, tanto 'e que subtraindo da aproximado 4,14 ja aplicando a formula certa da redondo certinho como fizeram os colegas baixo ou seja TR = TA / TI logo TR=1,0764/1,035 = 1,04 ou seja 4% redondo!!
parece bobeira mas numa prova de verdadeiro ou falso sem alternativas faz toda a diferenca!!
-
Cuidado com os comentários desses professores....
-
M = 5382
C = 5000
t = 6 meses = 1 semestre
inflação = 3,5% ao semestre
M = C + J
5382 = 5000 + J
J = 382
J = C x i x t
382 = 5000 x i x 1
i = 0,0764
ir = ((1 + i) / (1 + inflação)) -1
ir = ((1 + 0,0764) / (1 + 0,035)) - 1
ir = 1,04 - 1 = 0,4 ou 4 %
Resposta = B
-
A taxa de juros aparente, ou nominal, é aquela que leva 5000 reais a 5382 reais:

Sendo a inflação i = 3,5% neste período, então a taxa de juros real é:

Resposta: B