-
Gabarito Letra D
Uma forma segura para saber quantos kits que a entidade conseguirá montar se faz por meio da utilização do MDC (maximo divisor comum):
Para acharmos, temos que fatorar os números dados na questão e multiplicar aquele que consegue dividir TODOS os números,vejamos:
60 72 108 2
30 36 54 2
15 18 27 2
15 9 27 3
5 3 9 3
5 1 3 3
5 1 1 5
Os números em negrito conseguem dividir o 60, 72 e 108 simultaneamente, logo basta multiplicalos eacharemos a quantidadede kits
2x2x3=12
bons estudos
-
Renato, minha resolução foi igual a sua mas, aí não acreditei no resultado e fui logo ver o seu comentário, hahahaha. Veja o nível de autoconfiança. O que me deixou desconfiada foi que na questão, ele fala que todas as 240 peças são utilizadas nos kits. E aí, como fica???
-
Eu ficaria muito grato se alguém explicasse a ideia por trás dessa multiplicação. O que significa multiplicar 2, 2 e 3? Entender o raciocínio ajudaria a aplicar essa resolução em outras questões. :D
-
Vou tentar explicar. Parece paradoxal, mas como sou ruim de matemática, meu modo de explicar pode ajudar quem tem a mesma dificuldade.
Aprendi nos "macetes" das aulas por aí que, geralmente, nas questões desse tipo, pode-se usar o MDC para saber o maior divisor comum entre os números envolvidos.
Então, o primeiro passo é tirar o MDC de 60, 72, 108. O processo já foi postado, o resultado é 12. Serão 12 kits porque não é possível fazer mais de 12 kits iguais, já que é o MÁXIMO divisor comum entre os números dados. Kits IGUAIS significa a mesma quantidade de cada item em todos os kits, portanto, tem divisor COMUM envolvido.
Se você dividir o número de cobertores, casacos e calças por 12, verá quantos itens de cada um terá nos 12 kits:
60 : 12 = 5 cobertores;
72 : 12 = 6 casacos
108 : 12 = 9 calças.
Significa que serão 12 kits e CADA KIT terá: 5 cobertores, 6 casacos e 9 calças. É importante entender isso pois a questão poderia pedir a quantidade máxima de um item específico, por exemplo. Conhecendo a FCC, na próxima prova podem pedir isso ao invés da quantidade de kits, ou mesmo a SOMA de 2 itens específicos, então fiquem atentos, pois basta dividir a quantidade de cada item pelo MDC.
Mas para entender o processo, precisa-se estudar a FATORAÇÃO, MMC e MDC. Por que se multiplicou 2.2.3?
Fatorar é o mesmo que seguir dividindo pelo menor primo possível até que não seja mais possível dividir e o resultado seja "1". Exemplos de primos mais usados na fatoração: 2, 3, 5, 7...
No MMC (mínimo ou menor múltiplo comum), você multiplica TODOS os primos que serviram de divisores para os números: no caso da questão, o MMC seria 2.2.2.3.3.3.5 = 1080, esse é o MENOR múltiplo COMUM entre 60, 72 e 108.
Já o MDC (Máximo ou maior divisor comum), é o MAIOR número que pode dividir todos ao mesmo tempo. Ao contrario do MMC, onde vc multiplica todos os primos que serviram de divisores, no MDC vc só usa os que serviram para dividir TODOS ao mesmo tempo. Usarei até a postagem do colega Renato, mas destacarei:
60 72 108 2 - Veja que o 2 dividiu todos, é divisor comum.
30 36 54 2 - Novamente, o 2 dividiu todos, é divisor comum.
15 18 27 2 - Aqui, o 2 NÃO dividiu todos, NÃO É divisor comum
15 9 27 3 - O 3 dividiu todos, é divisor comum.
5 3 9 3 - Dividiu apenas o 3 e 9, não é comum
5 1 3 3 - Dividiu apenas o 3, não é comum
5 1 1 5 - dividiu apenas o 5, não é comum
O MDC é o produto dos divisores comuns: 2.2.3 = 12.
Isso que precisa dominar para entender o que foi feito. Recomendo as seguintes aulas:
https://www.youtube.com/watch?v=Z5G3aDjNPeY
https://www.youtube.com/watch?v=HWe6Vy4pd4o
https://www.youtube.com/watch?v=l-_TRAn5xRw
-
Amanda, são 240 peças: 60 cobertores + 72 casacos + 108 calças. :P
-
Gente, eu entendi da seguinte forma a questão da utilização das 240 peças:
Como Renato falou, temos o máximo divisor comum igual a 12. Se dividirmos cada quantidade de peças por 12, teremos 12 kits compostos por 5 cobertores, 6 casacos e 9 calças e, então, conseguiremos utilizar as 240 peças. Não sei se estou certa, mas entendi assim!
Abraço!
-
Galerinha,
MDC, beleza?
240, 72, 60 --- O máximo de divisores que são comuns aos três números são 12. Fechou!
Testaí!
-
O máximo divisor comum entre números é a multiplicação dos números que dividem, ao mesmo tempo, todos os números em análise.
60 , 72 , 108 -- 2
30 , 36 , 54 -- 2
15 , 18 , 27 -- 2
15 , 9 , 27 -- 3
5 , 3 , 9 -- 3
5 , 1 , 3 -- 3
5 , 1 , 1 -- 5
1 , 1 , 1
Os números em vermelho são aqueles que dividiram todos os números anteriores. A multiplição deles é que dará o MDC.
2 * 2 * 3 = 12
-
Minha matéria predileta, vou tentar elucidar todas as dúvidas, ok?
Aproveito para deixar uma dica fundamental, o jeito mais fácil de aprender lógica é fazendo 5 questões diariamente.
- Como descubro se a questão é de MMC (Mínimo Múltiplo Comum) ou MDC (Máximo Divisor Comum)?
A questão dirá essa informação para você, para não ficar muito longo, destacarei os termos que entregam tratar-se de um MDC.
Máximo: "...o número máximo de kits..."
Divisor: "...distribuir em creches da cidade..." (se ela vai distribuir, logicamente haverá uma divisão!)
Comum: "Se todos os kits são iguais..."
- Após essa etapa, vamos à resolução.
(i) Os dados da questão são:
60 cobertores, 72 casacos, 108 calças
Total: 240 itens.
(ii) Como estamos diante de um MDC, precisaremos de números que possam fazer a divisão SIMULTÂNEA dos três elementos.
60, 72, 108 | 2
30, 36, 54 | 2
15, 18, 27 | 3
5, 6, 9
(iii) Notem que não existe 1 número que divida ao mesmo tempo 5, 6 e 9. Sabe o que eles significam?
Resposta é bem simples: que em cada kit montado haverá: 5 cobertores, 6 casacos e 9 calças!
Somando estes valores, ficamos sabendo que em cada kit haverá 20 itens.
(iv-a) Sabendo dessa informação, vamos pegar o total de itens disponíveis (240) e dividir pela quantidade de itens que haverá em cada kit :
240 / 20 = 12.
(iv-b) Outro modo é usando os divisores comuns (muitos colegas fizeram assim), multiplicando os algarismos: 2, 2 e 3.
2x2x3 = 12.
(v) Eis a resposta, letra (D).
NOTA: Prefiro fazer MDC utilizando este método (só dividir quando tudo possa ser divivido ao mesmo tempo). O outro método (decompor todo o número e depois localizar aqueles em comum) é mais recomendado para o MMC.
Eventuais dúvidas ou erros, favor enviar uma mensagem.
At.te, CW.
-
-
CW, bem que você poderia comentar mais questões de matemática!!hahha
Ajudou muito!! obrigada!
-
É bem simples. Sempre quando a questão pede o máximo, será MDC.
MDC de 60, 72 e 108.
60, 72, 108 | 2
30, 36, 54 | 2
15, 18, 27 | 3
5, 6, 9 | ------
2x2x3 = 12
O que sobrar não serve, pois no MDC tem que dividir todo mundo.
-
Alguém sabe falar em qual tema do edital estaria enquadradas as questões que pedem mmc e mdc?
Os filtros não estão ajudando
-
Alana,
Geralmente eles só citam matemática básica.
-
SOCORRO!!! Alguém pode me explicar porque não pode ser 60?
60 cobertores /72 casacos / 108 calças = kits máximo e com números iguais de peças pela lógica só pode ser 60.
-
Pamela todos as 240 peças são utilizadas no kit. Para fazer 60 kits e todos terem o mesmo número de peças, não teria como utilzar todos as peças do kit, pois sobraria peças...
-
mdc de 60, 72 e 108.
-
GABARITO: Letra D
Caso você não soubesse resolver pelo M.D.C, era só ir dividindo cada valor das alternativas pelo número de vestimentas. A resposta é aquela em que se possa obter o maior valor exato em cada divisão !
Logo, oberseva-se que os únicos números divisíveis pelas vestimentas (60, 72 e 108) são os números 12 (Alternativa D) e 6 (alternativa E).
A resposta será 12, pois ele quer o maior número de kits !
Bons estudos !
-
GAB D
QUANDO DEVO ULTILIZAR:
MDC: MÍNIMO, MÁXIMO, MAIOR, MENOR E SEMELHANTES
MMC: AO MESMO TEMPO, CONJUNTAMENTE E SEMELHANTES
-
Sinceramente,eu achei a questão mal elaborada , pois o MDC é o maior divisor comun. Só que a questão pede o maior número de KITs possíveis , ou seja, tem que ser o menor divisor comun que é 1 , desta forma a questão é 60 Kits.Bom vou tenta explicar são 240 peças ao todo , só que são 3 variedades de roupas. Dessa forma, é apenas dividir por 3 os 240 que dá 80 peças de roupas para cada variedade. O único problema é que temos apenas 60 cobertores , então poderemos apenas utlizar 60 cobertores em cada KIT. Concluimos que o maior número de KITS são 60. Se estiver errado no meu raciocínio , por favor me corrijam.
Bons estudos a todos
-
LETRA D
pode ser resolvido por duas formas simples.
por MDC:
60/72/108 = 12
ou analisando pelas alternativas, onde todos os números (60,72 e 108) são divisíveis por 12.
-
para calcular o MDC voce deve multiplicar apenas os números que são divisiveis ao MESMO TEMPO:
60 72 108 2 > divide todos
30 36 54 2 > divide todos
15 18 27 2 > so divide o 18
15 9 27 3 > divide todos
5 3 9 3 3 > so divide o 3 e o 9 LOGO, multiplique APENAS o que divide os 3 ao mesmo tempo
5 1 3 3 3 > so divide o 3 2x2x3 = 12 Letra D
5 1 1 5 5 > so divide o 5
1, 1, 1, 1
-
Muito obrigada, CW.
-
pensei da seguinte forma:
Já que os kits devem ser idênticos, devo achar a diferença dos dois menores valores das vestimentas e esse deve ser um número que seja divisível pelas 3 quantidades, então:
72 - 60 = 12 ---> p/ conferir divide os valores de vestimentas por 12.
60/12 = 5
72/12 = 6
108/12 = 9
logo serão 12 kits com
5 cbertores, 6 Casacos e 9 Calças
-
Caros,
Maxímo divisor comum (60, 72, 108) = 12;
Método: realizar o MMC tradicional e multiplicar apenas os números que dividem ambos os três números. No caso: 2 x 2 x 3 : 12.
Dúvidas: Inbox.
~Frase de Impacto ~
-
A questão pede para não sobrar peças, logo... não pode haver resto na divisão...
Então, basta dividirmos 60, 72 e 108 por cada um dos valores das alternativas.
O que não houver resto, será nossa resposta, que no caso será a letra (d) 12, pois ele é o único valor dentre as alternativas que divide 60, 72 e 108 e não há resto.
-
Aplicando a regra do MDC resolve a questão. Os colegas já detalharam, brilhantemente, a resolução.
Avante sempre!
-
boa questao!
-
GABARITO: D
Resolução: https://www.youtube.com/watch?v=k40wmG1znLI
-
-
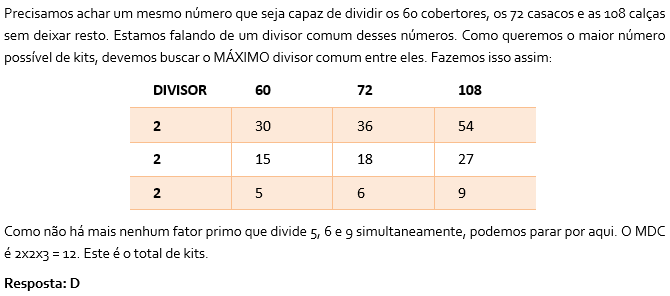
Resolução
https://www.youtube.com/watch?v=NUduU5zZB4M
-
Aqui não entendi. Quando se tira o MDC dos números se chega a 12, até aqui tudo bem. No caso este não é o número de peças por kit?