-
Correto Letra D
Montando um gráfico com as informações do probrema, temos um diagrama de Venn com a seguinte forma:
→ Três circulos, que podemos chamar de A,B e C em referência às empresas, interconectando-se.
→ Na interconecção central, o problema informou que apenas 1 atleta está presente (Carlos é o único atleta que tem patrocínio de 3 empresas).
→ Na intersecção entre A e B, temos 2 ( Leandro e Hamilton, das empresas A e B )
→ Na intersecção entre A e C, temos 2 ( Marta e Silas, das empresas A e C )
→ Na intersecção emtre B e C, temos 3 ( Amanda, Renata e Sérgio, das empresas B e C )
Feito esse desenho, o problema informa que " cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela ".
Também informa que o número total de atletas é 18.
Por último, o problema nos pergunta as quantidades mínima e máxima de atletas que podem ser patrocinados pela empresa B.
Considerando que o número de atletas é 18 e que 8 destes já estão inclusos no gráfico, restam 10 para seren distribuídos pelas partes dos círculos que não interconectam-se com outros círculos (partes que deixamos vazias quando montamos o diagrama).
Para determinarmos o número mínimo de atletas que B pode patrocinar, basta preenchermos o espaço vazio em B com o número 1, já que cada empresa patrocina pelo menos 1 entleta de forma exlcusiva. Em seguinda, somamos todos os atletas que B patrocina, de forma exclusiva ou não:
1 + 2 + 1 + 3 = 7
Para determinarmos o número máximo que B pode patrocinar, basta preenchermos a parte vazia do círculo A com 1, a parte vazia do círculo C com 1 e colocarmos 8 na parte vazia de B. Esse número 8 é encontrado ao lembrarmos que restavam 10 atletas para serem distribuídos pelo gráfico, sendo que cada parte ainda vazia dos círculos precisa conter pelo menos 1 ( cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela ). Logo 10 - 2 = 8.
Somando então todos os atletas que B pode patrocinar no máximo, temos seguinte:
8 + 2 + 1 + 3 = 14
-
Mínimo:
Carlos, Leandro, Hamilton, Amanda, Renata e Sérgio + 1 que recebe patrocínio só da empresa B = 7
Máximo:
Carlos, Leandro, Hamilton, Amanda, Renata e Sérgio + 8 (exclui 1 que recebe só da A e um que recebe só da C) = 14
Gabarito letra D.
-
tinha esquecido do mais 1
-
https://www.youtube.com/watch?v=j4waogLOzXs#t=3.304655
-
Resposta D
Montando um gráfico com as informações da questão
interseção ABC = 1 Carlos
interseção AB = 2 leandro e hamilton
interseção AC = 2 marta e silas
interseção BC = 3 amanda renata e sergio (até agora 8 pessoas)
interseção A = 1 "pelo menos um atelta exclusivo"
interseção B = 1 "pelo menos um atelta exclusivo"
interseção C = 1 "pelo menos um atelta exclusivo" (até agora 11 pessoas)
(7 "ficaram voando" que poder ser de A,B ou C para fechar os 18)
Minimo = 1 (abc) + 2 (ab) + 3 (bc) + 1 (exclusivo) = 7
Máximo = 1 (abc) + 2 (ab) + 3 (bc) + 1 (exclusivo) + 7 (voando) = 14
#qconcurso + #esforço&motivação + #féemDeus + #lazer&amigos = #aprovação
-
Contando Bs:
C: A, B e C.
L e H:A e B;
A, R e Sérgio: B e C.
1+2+3 = 6.
Se esses atletas fazem parte de um grupo contendo, ao todo, 18 atletas que recebem patrocínio das empresas A, B ou C, e cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela, (significa que deve haver mais B's além dos 6 anteriores, pelo menos 1, o número mínimo) então é correto afirmar que os números mínimo e máximo de atletas que a empresa B pode patrocinar são, respectivamente,
6+1=7
-
-
Em concurso publico e vestibular não se pode perder tempo. É óbvio que o mínimo é 7 (6 dos exemplos citados + 1 do exclusivo) a unica alternativa que possui como mínimo o 7 é a D. Não interessa a resolução do maior, próxima questão. Dica de ouro: "não se complica o simples."
-
Max:
18 - (3 + 1) = 14
Min
14 / 2 = 7
-
o vídeo da resolução está no link:
https://youtu.be/q_hrlSl0dAg
-
Yan soleto ta certissimo
-
o que quebrou foi ter que colocar mais 1 para o Carlos na interseção já que ele já era patrocinado pelas 3 empresas.....
-
https://www.youtube.com/watch?v=10kJmQVwKpY
-
Basta preencher com a informações dadas no enunciado, e depois :
Por 1 no apenas B (mínimo)
Por 1 no apenas A e no apenas C (máximo)
-
Mínimo:
Carlos, Leandro, Hamilton, Amanda, Renata e Sérgio + 1 que recebe patrocínio só da empresa B = 7
Máximo:
Carlos, Leandro, Hamilton, Amanda, Renata e Sérgio + 1 sem nome + 7(voando) = 14
Demorou para entender que :
1º Somando todos as pessoas que a questão fala da 11(contando ja com os exclusivos em cada uma)
2º que o total são 18 pessoas ( 18-11= 7 esses 7 pode estar em qualquer
empresa então é possivel esses 7 estarem na b ...
3º somando o 7(minimo)+7(voando) = o máximo só pode ser14 )
-
Se achar o mínimo já mata a questão:
Empresa B: Carlos, Leandro, Hamilton, Amanda, Renata, Sérgio e mais 1 (recebendo patrocínio só dela). = 7.
-
O comando dessa questão não ficou claro o suficiente. Mas temos que nos adaptar. Para facilitar o entendimento da questão interprete assim:
1) Quem a empresa B já patrocina?
L e A (AB), K (ABC), A e R e S (BC) e Exclusivo = 7
2) Se patrocinar outros atletas (ainda nao mencionados), quantos atletas a empresa B estará patrocinando?
18 podem ser patrocinados, e ao todo a questão cita que estão sendo 11 patrocinados.
Logo, restam sem patrocínio mais 7 (18 - 11 = 7). B Max = 7 + 7 = 14
-
QUESTAO DE DIFICIL ENTENDIMENTO,A BANCA DEVERIA SER MAIS CLARA...
-
ABC=1 + AB=2 + BC=3 + B=1 ......temos o mínimo de 7 em B
Agora, para o máximo temos em B = 1 + X
ABC=1 + AB=2 + BC=3 + AC=2 + A=1 + B=(1+X) + C=1 = 18 (TOTAL)........temos X=7
Agora é pura análise: no conj. A, se temos o mínimo de 7 . O máximo será o mínimo mais alguma coisa (X).....= 14
-
Correção da prova de Escrevente pelo Neaf - https://www.youtube.com/watch?v=XuRXTmB6WwI
Segundo o professor:
Pelo menos 6 são patrocinados por B confome as interseções + 1 esclusivo da empresa B> total 7
Sabemos que há um total de 18 pessoas, dessas 7 são o mínimo patrocinado por B. 18-7= 11
Dstas 11 pessoas há pelo menos 2 que são patrocinadas respectivamente somente por A e somente por B, restando um total de 9.
Destas 9 há ainda Marta e Silas que são patrocinados por A e C, ou seja, não há relação com B. Sendo assim, 9-2= 7
B= 7 no mínimo + 7 (que sobraram e que não faziam parte da relação com B)máximo = 14.
Eu não tinha entendido os 14 restantes, achei essa explicação a melhor que assisti. Espero que ajude a alguém como me ajudou. :)
-
Só por raciocínio e exclusão - veja:
"... grupo contendo, ao todo, 18 atletas que recebem patrocínio das empresas A, B ou C ..."
18 / 3 = 6 (18 atletas dividido por 3 empresas) = (temos 6 atletas no MÍNIMO patrocinados por A, B ou C)
"... cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela ..."
ou seja: + 1 EXCLUSIVO
logo:
6 + 1 = 7
A única alternativa que contém o mínimo 7 é a letra D.
-
Na empresa B: Leandro, Hamilton, Carlos, Amanda, Renata e Sérgio + 1 (que será patrocinado EXCLUSIVAMENTE pela B)
Leandro 1 + Hamilton 2 + Carlos 3 + Amanda 4 + Renata 5 + Sérgio 6 + o exclusivo 7
No mínimo 7
Já achar o máximo eu não sei rs
-
Como Achar o número máximo:
Se sabemos que há 7 pessoas sendo patrocionadas, pelo grupo B e temos 4 pessoas sendo patrocinadas pelo grupo A E C, fazemos:
18-4= 14
Só subtrair do total o que esta no grupo restante.
Abs
-
Acertei achando apenas o mínimo. A única alternativa com o mínimo de 7 é a D. Segue o baile.
-
18 atletas das empresas A, B, e C +3 (1 de cada empresa)
18+3=21
21/3 = 7
Sobrou = 14
Min. 7 e Máx. 14
Gab. D
-
Obrigado pessoal pelas resoluções.
-
Mínimo de atletas em B:
1 - Carlos (A,B,C)
2 - Leandro (A,B)
3 - Hamilton (A,B)
4 - Amanda (B,C)
5 - Renata (B,C)
6 - Sérgio (B,C)
7 - Atleta exclusivo (B)
Máximo de atletas em B:
1 - Marta (A,C)
2 - Silas (A,C)
3 - Atleta exclusivo (A)
4 - Atleta excluvivo (C)
18 atletas no total - 4 = 14
-
À primeira leitura, parece difícil, mas é só saber que a empresa B está patrocinando 6 atletas já citados, + pelo menos 1 que recebe patrocínio somente dela, que temos o valor de 7, que só se encontra na Alternativa D!
Bons estudos!!!!
-
TEORIA DA CASA DOS POMBOS
(Casa=Empresa; Elemento=Atleta)
Distribui-se os elementos em cada casa conforme orienta a questão. Teremos 6 atletas na casa "B" (que é a de nosso interesse).
O enunciado informou o nome de 8 atletas de um total de 18, ou seja, restam 10 para serem distribuidos entre A, B e C.
Sabe-se que 3 dos 10 atletas restantes já possuem suas respectivas casas (um em cada).
Logo, obtemos o número MÍNIMO de 7 atletas na "B" (lembrando que ainda temos 7 atletas sem "casa").
De acordo com a teoria da casa dos pombos, podemos distribuir os elementos restantes aleatoriamente entre as casas.
Isto significa que podemos distribuir NENHUM ou até 7 atletas em qualquer uma das casas, inclusive na "B".
Suponha-se que todos os 7 atletas foram distribuídos na casa "B": 7 já existentes + 7 restantes = 14 (que é o número MÁXIMO de elementos possíveis nesta).
DICA: Para ficar mais claro, seria interessante assistir a uma explicação sobre a Teoria da Casa dos Pombos no Youtube, uma vez que esta não vem explicita no edital do TJ/SP.
-
Encontrando o mínimo acha-se o máxino
-
Não sei se essa pode ser a sua dúvida, mas a minha foi: O que significa esse tal de 7 voando?!?!?
Entendi o seguinte: Carlos, Leandro, Hamilton, Amanda, Renata, Sérgio, Marta, Silas + 3 atletas que só tem um patrocinador = 11 pessoas!
Sabemos que o total de pessoas é 18, então 18-11 = 7 .. que é o tal dessas pessoas voando ( pessoas que não tem um destino certo no enunciado) essas pessoas podem ser patronicionados por qualquer dessas três empresa, ou seja, pode ser patroninada por B.
Aí é só somar os 7 - que é o mínimo + esses 7 = 14
-
seja x,y,z os atletas patrocidados exclusivamente por A.B,C
a dica é fazer diagrama de ven vemos que x+y+z = 10
pelo texto o minimo de y=1 entao Bmin=7 ....
para saber o max, considere x e z minimo 1, entao y=8 e B=14
-
Excluíndo-se os atletas exclusivos de A e C, bem como Marta e Silas, que não são patrocinados por B, todo o restante pode ter patrocínio de B, logo, 14.
-
Veja no diagrama abaixo as informações do enunciado. Note que coloquei 1 pessoa no centro, pois somente Carlos é patrocinado pelas empresas. Coloquei 2 pessoas na interseção apenas entre A e B (Leandro e Hamilton), 2 pessoas na interseção apenas entre A e C (Marta e Silas), e 3 pessoas na interseção apenas entre B e C (Amanda, Renata e Sérgio). Chamei de X, Y e Z as quantidades de pessoas patrocinadas somente por A, B e C, respectivamente.
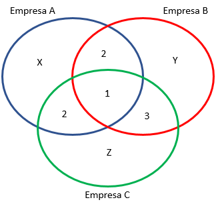
Sabemos que X, Y e Z devem ser, no mínimo, iguais a 1. Isto porque cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela.
Para obter o MAIOR valor possível para Y, devemos considerar que X e Z são os menores possíveis, ou seja, X = 1 e Z = 1. O total de pessoas é 18, logo,
18 = X + 2 + 1 + 2 + Y + 3 + Z
18 = 1 + 2 + 1 + 2 + Y + 3 + 1
18 = 10 + Y
Y= 8
Neste cenário, o número máximo de pessoas patrocinadas pela empresa B é:
2+1+3+Y = 2+1+3+8 = 14
Para obter o mínimo, basta considerar Y = 1, que é o seu menor valor possível. Assim, o número mínimo de pessoas patrocinadas por B é:
2+1+3+1 e= 7
Resposta: D
-
Alguém resolveu sem desenhar algum esquema ou equação? Direto "de cabeça"?
Apenas fui dando "nome aos bois", e descobri que na empresa em B ficaram as seguintes pessoas: Carlos (ABC), Leandro (AB), Hamilton (AB), Amanda (BC) Renata (BC), Sérgio (BC), Pessoa sem nome (premissa do enunciado) (B).
Somando o número de pessoas, temos que 7 pessoas são certeza (ou seja, número mínimo de pessoas) que estão no grupo B.
Como só a alternativa D tem o número 7 como resposta, fui direto nela, sem ao menos precisar contar o número máximo de atletas.
-
Há umas explicações aqui surreais, fiz assim: o total são 18. 18-1= 17.
No total são 6 o patrocinados por B, logo : 17-6= 11.
Depois é só jogar o número total de atletas 18-11= 07.
acha-se assim o minimo.
Pessoal usando fórmula quântica, oloco*.
-
Para responder temos que somar todos os atletas que o enunciado nos dá como sendo patrocinados pela empresa b, que são: L, H, C, A, R, S.
Total 6.
Porém o enunciado diz que cada empresa patrocina exclusivamente pelo menos um atleta, então, somando-se esse um atleta, temos 7 atletas na empresa B. Esse é o mínimo.
Se são 18 atletas no total, excluímos esses 7 do total de 18,e restam 11. Desses 11 excluímos 4, pois são os 2 que seriam patrocinados exclusivamente pelas empresas A e C, e os dois que são patrocinados por ambas as duas A e C ( os atletas S e M).
Sobram 7 atletas. Jogamos esses 07 todos no conjunto b, que ficaria 7+7=14. Pronto, mínimo 7 máximo 14.
-
Estava estudando Diagrama de Veen.. achei fácil até começar essas questões complicadas que preciso de uma bola de cristal para entender .. kkk
-
Gabarito:D
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
-
https://www.youtube.com/watch?v=XuRXTmB6WwI 25:02
-
Carlos é o único atleta que tem patrocínio de 3 empresas: A, B e C. Em se tratando de atletas que recebem patrocínios de apenas 2 dessas empresas, temos: Leandro e Hamilton, das empresas A e B; Marta e Silas, das empresas A e C; e Amanda, Renata e Sérgio, das empresas B e C. Se esses atletas fazem parte de um grupo contendo, ao todo, 18 atletas que recebem patrocínio das empresas A, B ou C, e cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela, então é correto afirmar que os números mínimo e máximo de atletas que a empresa B pode patrocinar são, respectivamente,
FIZ COM AUXÍLIO DO DIAGRAMA
QUANTIDADE MÍNIMA = CARLOS, LEANDRO, HAMILTON, AMANDA, RENATA, SÉRGIO E PELO MENOS + 1 ATLETA = 7
QUANTIDADE MÁXIMA = CARLOS, LEANDRO, HAMILTON, AMANDA, RENATA, SÉRGIO + 12 - 4 (MARTA, SILAS, O ATLETA PATROCINADO PELA EMPRESA A E O ATLETA PATROCINADO PELA EMPRESA C) = 6 + 8 = 14
A) 6 e 12.
B) 5 e 10.
C) 8 e 16.
D) 7 e 14.
E) 4 e 8.
-
Consegui matar essa pelo número mínimo.
Quando você preenche o diagrama, você percebe que:
- São 2 atletas em A + B
- São 3 atletas em B + C
- Apenas 1 atleta em A + B + C
O problema está perguntando o mínimo e o máximo que poderia ser patrocinado pelo B.
Vejamos:
Somando todos que fazem parte do B ali em cima, ja temos 6.
Se deve haver obrigatóriamente ao menos 1 em cada equipe, sendo patrocinado de forma isolada, então eu considerei colocar apenas 1 em B, ja que se trata do número mínimo.
Logo:
2 + 3 + 1 + 1 = 7
A única alternativa que contém número mínimo de 7 é a alternativa D.
GAB. D
-
Consegui matar essa pelo número mínimo.
Quando você preenche o diagrama, você percebe que:
- São 2 atletas em A + B
- São 3 atletas em B + C
- Apenas 1 atleta em A + B + C
O problema está perguntando o mínimo e o máximo que poderia ser patrocinado pelo B.
Vejamos:
Somando todos que fazem parte do B ali em cima, ja temos 6.
Se deve haver obrigatóriamente ao menos 1 em cada equipe, sendo patrocinado de forma isolada, então eu considerei colocar apenas 1 em B, ja que se trata do número mínimo.
Logo:
2 + 3 + 1 + 1 = 7
A única alternativa que contém número mínimo de 7 é a alternativa D.
GAB. D
-
Bom que eles colocaram nomes só para confundir mesmo.
-
Foi mais fácil do que o teste de 2018, mas mesmo assim.... temos tempo para responder as questões.
Eu resolvi desenhando os círculos (por Diagrama de Venn).
-
Dados da questão:
A + B + C = 1 pessoa.
A + B = 2 pessoas
A + C = 2 pessoas
B + C = 2 pessoas
Cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela. Então temos:
A = mínimo 1
B = mínimo 1
C = mínimo 1.
O problema quer os números mínimo e máximo de atletas que a empresa B, sendo assim:
Para acharmos o mínimo somamos todas as intercessões do B (2+1+3) e com o 1 que tem somente no B, já que na questão afirma que cada empresa tem pelo menos uma pessoa.
MÍNIMO: 2+1+3+1 = 7
Agora para achar o máximo, excluímos as pessoas que não tem em B. Sendo assim, excluímos 1 de somente A e uma pessoa que tem em somente B (lembrando que cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela). Depois excluímos as pessoas que compõem A e C, que são duas.
1+1+2 = 4 pessoas.
18 (total) - 4 pessoas que não estão em B = 14 pessoas. Este seria o máximo.
Sendo assim, GABARITO D: 7 E 14.
Para uma melhor visualização ====> https://jspaint.app/#local:d426b3d04ddba
-
Chocada que consegui fazer.
-
Questões de raciocínio tem que tomar muito cuidado, muitas vezes passam batidos dados importantíssimos, não tinha visto o Sérgio no enunciado...
-
Questões que envolvem diagrama de Venn precisa de muita prática e treino para resolver em menos tempo.
-
Legal é a professora falando: "simples assim" ... ai ai
-
https://www.youtube.com/watch?v=bYJ9RRxidbE
-
A questão é bem simples.
Faça um diagrama para observar melhor!
Em cada empresa, recebendo mais de 1 patrocínio, temos:
A= { L;H;C;M;S}
B= {R;S;A;C;L;H}
C= {C;R;S;A;M;S}
A questão diz que ao menos 1 atleta em cada empresa recebe patrocínio só dela. Ou seja, em A, B e C tem mais 1 além desses já citados.
Com isso já conseguimos responder.
Qual minimo que B pode ter, e isso é óbvio. B já tem 6 elementos + 1 atleta que é patrocinado só por B = 7
Aqui já mata a questão, visto que só tem uma alternativa que tem 7 como minimo.
Mas continuando, para descobri o máximo, teremos que contar quantos elementos existe no total:
Considerando só uma vez cada elemento, temos que - Atletas que recebem mais de um patrocínio são 8, somado com 3 atletas que recebem patrocínio de uma única empresa. temos 8+3=11
Do total de 18 atletas, só temos 18-11= 7 atletas que não sabemos onde estão.
E para B chegar ao máximo é esses 7 deverão está lá.
Então 7 (que já é os atletas que já estão em B) + 7 (dos que podem está em B) = 14 atletas
-
Respondi do jeito mais fácil que existe: Chutando kkkkkkkkkkkkkkkkkkkk se acertar no dia da prova, tá valendo! Tenho uma relação com esse tipo de questão complicada...não entra na cabeça!