-
Faça supondo a=1. Substituindo na equação acharemos que b=1,618.
-
É só colocar na base decimal as opções e substituir na igualdade . Se as igualdades forem iguais essa será a certa.
-
b/a = (a+b) / b
b/a = (a/b) +1
substituindo: x = b/a
x = (1/x) +1
x^2= x+1
resolvendo: x = 1,618
-
Se alguem puder me auxiliar nessa questão, não entendi.
Grato.
-
1a φ = b/a ---- > b = a φ
2a φ = (a+b)/b ------> b φ = a+b
Substitui o b por a φ na 2a
a φ^2 = a + a φ
Pode elminar o a da equação e fica:
φ^2 - φ - 1 = 0
Resolvendo chega nos 1,618 (só é complicado calcular o raiz de 5 na prova)
Abs!
-
Em que faculdade se aprende isso, pelo amor de Deus?!!!
-
Comentário do Ponto: https://www.pontodosconcursos.com.br/admin/imagens/upload/5923_D.pdf
-
X = B/A = (A + B)/B
X = A/B + B/B
X= A/B + 1
--------------------------------
SE X = B/A , ENTÃO A/B = 1/X;
--------------------------------
X = 1/X + 1
( MULTIPLICA TUDÃO POR X)
X2 = 1 + X
X2 - X - 1 = 0
---------------------------------
AGORA TENHA CORAGEM E RESOLVA A EQUAÇÃO DO 2O GRÁU;
-
Cheguei na equação do segundo grau, mas não consegui chegar na resposta.
Ao final da equação, cheguei na raiz quadrada de 5 sobre 2, mas resolvendo isso não chego em nenhuma das respostas. Alguém pode me ajudar?
-
Ao trabalhar a questão chegamos na equação x²-x+1=0, considerando x=b/a. As raízes vão resultar em (1+raiz(5))/2 e (1-raiz(5))/2.
Pra quem não souber de cabeça o valor aproximado de raiz 5, na hora da prova daria pra fazer uma estimativa rápida. Sabendo que raiz de 4 é 2, pode-se multiplicar 2,2*2,2 e 2,25*2,25 e ver que resultam em 4,84 e 5,0625, respectivamente. Então podemos considerar que raiz (5) é grosseiramente 2,25 (na realidade é 2,236067...). Substituindo nos valores encontrados inicialmente, teríamos:
(1+raiz(5))/2 = 1,625 (o valor mais próximo nas alternativas é 1,618, letra A)
(1+raiz(5))/2 = -0,625 (podemos descartar esse valor negativo)
-
Vamos manipular a igualdade:
Podemos considerar que b seja uma constante, e obter o valor da variável “a” em função de b aplicando a fórmula de Báskara:
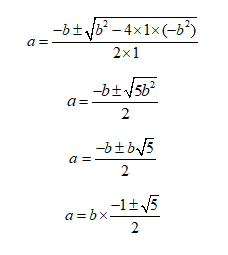
Usando a aproximação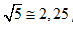 
temos:
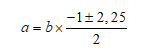
a = 0,625b ou a = -1,625b
Considerando a = 0,625b, temos:
φ = b/a = b / 0,625b = 1 / 0,625 = 1,6
Temos, aproximadamente, o resultado da alternativa A. Se você utilizar uma aproximação melhor para a raiz de 5, terá um resultado ainda mais próximo.
Note que, se considerássemos a = -1,625b, teríamos φ = -0,615, que não figura entre as alternativas de resposta.
Resposta: A
-
Vou escrever de uma forma bem detalhada. Pode ser mais demorado, mas pra quem tem dificuldade de desenvolver entende melhor.
O enunciado pede uma igualdade:
b/a = a+b/b sendo b maior que a
Como a questão não dá os valores de a e b, podemos chutar um valor para a, já que estão um em função do outro.
Vou chutar 1 para a: a=1
Agora só substituir
b/1= 1+b/b
Para chegar na equação do 2 grau, precisamos resolver as frações. Como os denominadores são diferentes, precisa tirar o MMC e nesse caso vai ser o produto entre eles: 1.b
b.b = 1.1+ b.1
1.b 1.b
Como já foi usado o 1.b para resolver as frações, podemos descartá-los. ficando apenas:
b²= 1+b
Para igualar a 0, inverta os sinais:
b² - b - 1= 0
Agora calcule o Delta:
D= b²-4.a.c
D= (-1)².4.1.(-1)
D= 5
Agora substitua na fórmula. (Queremos achar o valor de b)
b= -b +/- raiz de D / 2.a
b= -(-1)+/- raiz de 5 /2.1
b=1+/- raiz de 5 /2
Como a questão diz que b é maior que a, então ficamos apenas com a raiz positiva:
b=1+ raiz de 5/ 2
Para tirar a raiz sem calculadora:
RAIZ DE x = x + n²
2n
x= 5
n²= quadrado perfeito mais próximo (nesse caso o 4)
n= raiz do quadrado perfeito ( nesse caso 2)
substitua:
Raiz de 5= 5+4 / 2.2
Raiz de 5= 9/4 = 2,25
Agora volte e substitua na formula:
b= 1+ 2,25/ 2
b= 3,25/2
b=1,625
A questão pede a razão de b/a
1,625/1 = 1,625 (valor aproximado de 1,618)
Esse é o jeito de resolver sem calculadora. Com a raiz da calculadora teríamos obtido a resposta certinha. Mas como a questão pede o valor aproximado não tem problema.
-
Acho que esse povo está querendo doutores em matemática e não auditores-fiscais... pelo amor de Deus? Onde na vida um auditor fiscal vai aplicar uma mierda dessas? O povo tem que sabe r selecionar os candidatos dentro de uma razoabilidade... pohan