-
C(3,1) . C(5,1) + C(3,2) = 3 . 5 + 3 = 18
-
pessoal,
alguém pode escrever passo a passo essa questão? obrigada
-
EM PASSOS MIUDOS,
COM UMA MULHER POR EQUIPE TEMOS 03 MULHERES PARA 05 HOMENS. 3*5 = 15
COM DUAS MULHERES NA EQUIPE PODEREMOS TER 03 EQUIPES.
ENTÃO 15+3=18
-
Você usa a regra do pelo menos um... observe que ele quer que em cada equipe tenha pelo menos uma mulher, logo, não poderão ter dois homens em uma equipe. Seguindo esse raciocinio você faz a combinação do total que é C8,2 = 28, isso é se pudesse tudo, menos o que não pode acontecer que é ter dois homens numa equipe que é a C5,2 = 10. No final você subtrai (o todo) 28 - 10(o que não pode acontcer) = 18
-
Equipes com 2 pessoas, sendo pelo menos 1 mulher, podem ser formadas por:
-1 mulher e 1 homem (C3,1 x C5,1) = 3x5 = 15
-ou duas mulheres (C3,2) = 3
15+3=18
-
Quantas comissões posso formar desconsiderando a condição (havendo em cada equipe pelo menos uma mulher)?
c 8,2=28
Quantas comissões posso forma só com homem?
C5,2= 10
28 -10=18 comissões com pelo menos uma mulher
-
Existem 2 maneiras de resolver essa questão. A primeira é mais trabalhosa, mais demorada, mas mais fácil de raciocinar, a segunda é mais rápida, mas mais fácil de errar no raciocínio do meu ponto de vista.
- PRIMEIRA FORMA DE RESOLVER: por etapas. Se o grupo deve ter 2 pessoas, e pelo menos uma deve ser mulher, significa dizer que teremos grupos formados por uma mulher e um homem E grupos formados por duas mulheres, ok?
Assim:
- Grupo com 1 mulher = C 5,1 x C 3 , 1 = explicando o que eu fiz: na primeira combinação desse grupo formado por um homem e uma mulher, de 5 homens eu escolho um, e de 3 mulheres eu escolho 1.
Fórmula da combinação: n!/p! (n-p)! = CALMA!!! A FÓRMULA PARECE DIFÍCIL MAS NÃO É NA PRÁTICA!!!!
C5,1 X C 3,1 = 5! /1! 4! X 3! / 1! 2! = 5 X 4!/ 4! X 3X2! / 2! = 15
- Grupo composto por 2 mulheres fica = C3,2 , isto é, de 3 mulheres, eu escolho 2
Substituindo a fórmula fica: C3,2 = 3! / 2!1! = 3x2! / 2! x 1 = 3
Já que esses eventos não precisar acontecer ao mesmo tempo, eu somo as possibilidades encontradas nos diferentes grupos = 15 + 3 = 18
-
A outra forma mais rápida de fazer, porém mais fácil de errar, é realizar o grupo total e subtrair do que não pode ocorrer no fato.
Temos um total de 8 pessoas e devemos escolher apenas 2 delas = C8,2
Como sempre temos que ter pelo menos uma mulher no grupo de 2 pessoas, é impossível ter dois homens no grupo, correto? Então não pode de jeito nenhum ser dos 5 homens existentes, dois escolhidos. O máximo de homens escolhidos, será sempre 1.
Assim não pode C5,2
Resultado: C8,2 - C 5,2 = Substituindo na fórmula
8! / 2! 6! - 5! / 2! 3! = 8x7x6! / 2x1x6! - 5x4x3! / 2x1x3! = cortando os fatoriais fica = 56 / 2 - 20 / 10 = 28 - 10 = 18
-
Fiz da seguinte forma:
C(5,1)*C(3,1)= 15 possibilidades de formar uma dupla mista.
Mas ainda existem as possibilidades de duplas formada por duas mulheres representadas por: C(3,2)= 3.
Somando as duas possibilidades tem-se o valor de 18.
-
5h 3m (5 homens 3 mulheres)
Combinações possíveis para mulher 1 (m1)
5*m1
Combinações possíveis para mulher 2 (m2)
5*m2
Combinações possíveis para mulher 3 (m3)
5*m3
Total de 15 combinações possíveis com 1h 1m
Combinações possíveis entre mulheres:
m1/m2
m1/m3
m2/m3
Total de combinações possíveis: 15 + 3 = 18
Gabarito: D
-
Para os colegas que vem esse C8,2 = 28 e ficam viajando: 8/2 x 7/1 = 28 equipes (total)
Com a restrição: apenas não pode equipe só de homem C5,2 = 10: 5/2 x 4/1 = 10 equipes (restrição)
-
Gabarito: Letra D
ATENÇÃO!!! Veja que podemos ter equipes com 1 mulher e 1 homem, ou equipes com 2 mulheres.
1) No primeiro caso, precisamos combinar 3 mulheres, 1 a 1, e combinar 5 homens, 1 a 1:
C (3,1) = 3
C (5,1) = 5
Portanto, é possível formar 3 x 5 = 15 equipes distintas.
2) No segundo caso, precisamos apenas combinar as 3 mulheres, 2 a 2:
C (3,2) = 3x2/2x1 = 3
Assim, podemos formar 3 equipes distintas.
Logo, ao todo temos 15 + 3 = 18 equipes distintas.
Fonte: ESTRATÉGIA CONCURSOS
-
RESOLUÇÃO:
Veja que podemos ter equipes com 1 mulher e 1 homem, ou equipes com 2
mulheres.
No primeiro caso, precisamos combinar 3 mulheres, 1 a 1, e combinar 5
homens, 1 a 1:
C(3,1) = 3
C(5,1) = 5
Portanto, é possível formar 3 x 5 = 15 equipes distintas.
No segundo caso, precisamos apenas combinar as 3 mulheres, 2 a 2:
C (3,2) =
3X2 / 2X1 = 3
Assim, podemos formar 3 equipes distintas. Ao todo, temos 15 + 3 = 18
equipes distintas.
Resposta: D
Prof: Arthur Lima.
-
Esse tipo de questão que fala "pelo menos um" é melhor fazer da seguinte maneira:
Total - o que a questão não quer
Total = C 8,2 = 28 (Total de equipes com homens e mulheres)
O que a questão não quer = C 5,2 = 10 (Total de equipes só com homens)
C 8,2 - C 5,2 =
28 - 10 =
18
-
Veja que podemos ter equipes com 1 mulher e 1 homem, ou equipes com 2 mulheres.
No primeiro caso, precisamos combinar 3 mulheres, 1 a 1, e combinar 5 homens, 1 a 1:
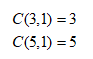
Portanto, é possível formar 3 x 5 = 15 equipes distintas.
No segundo caso, precisamos apenas combinar as 3 mulheres, 2 a 2:

Assim, podemos formar 3 equipes distintas. Ao todo, temos 15 + 3 = 18 equipes distintas.
Resposta: D