-
ALTERNATIVA CORRETA B
Podemos resolver essa questão usando o macete para problemas com 2 conjuntos em que é solicitada a interseção. Basta somar as quantidades de elementos dos dois conjuntos (42 + 95 = 137) e subtrair o total (120), ficando com 137 – 120 = 17 pessoas na interseção, ou seja, pessoas que recebem os dois benefícios.
-
GABA: B
Conjunto Universo =120
VALE Transp = 42 + 95 Vale Refeição = 137
137-120 = 17 interseção
-
Dica Chico Trt
ALTERNATIVA CORRETA B
Podemos resolver essa questão usando o macete para problemas com 2 conjuntos em que é solicitada a interseção. Basta somar as quantidades de elementos dos dois conjuntos (42 + 95 = 137) e subtrair o total (120), ficando com 137 – 120 = 17 pessoas na interseção, ou seja, pessoas que recebem os dois benefícios.
-
120 - 42 (que recebem vale transporte) = 78
120 - 95 (que recebem vale refeição) = 25
25+78=103
120-103=17
-
Soma todos os valores e subtrai o total, acha-se o valor da interseção, pedido pela questão. Letra B.
-
Gab: B.
Soma todos os valores, diminui do valor total. A diferença é a interseção. :))
95 + 32 = 137
137 - 120 = 17.
-
Olá pessoal,
Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/_IQNBFP-J4Y
Professor Ivan Chagas
Gostou? Doe: https://pag.ae/blxHLHy
-
TOTAL = 120
VT = 42 - x
VR = 95 - x
VT e VR = x (o que eu procuro)
42 - x + x + 95 - x = 120
137 - x = 120
x = 17
-
Total = 120
VT = 42
VR = 95
95 + 42 = 137
137 - 120 = 17
-
Não é difícil,basta:
95+42=137-120=17funcionários recebem os dois benefícios.
Teria que achar a interseção, que é só somar o total da quantidade dos benefícios um com outro, então,pega o resultado dessa adição e subtraí com total de funcionários.
-
AuB=N(A)+N(B)-N(A união B)
-
Eu fiz da seguinte forma: 95+42=137
137-120= 17
-
A inter B=42+95-120=17
-
Resolução
quant. vale-transporte = 42 n(T)
quant. vale-refeição = 95 n(V)
total = 120
Cálculo
120 = n(T) + n(V) - n(T ∩ V)
120 = 42 + 95 - X
120 = 137 - X
X = 137 - 120
X = 17
GABARITO: B
-
Letra B
Exercício com raciocinio indentico no vídeo YOUTUBE , segue olink:
https://www.youtube.com/watch?v=_2TOX0YI0LM
-
95+42=137
137-120= 17
BINGO
-
Além da interseção eu pensei no probleminha prático em que a empresa tem 137 benefícios para distribuir para 120 funcionários. Distribuindo os benefícios para todos ainda sobram 17, daí esses 17 começam a serem novamente distribuídos para os primeiros da fila, logo os 17 primeiros terão a sorte de receber os 2 benefícios.
-
Teoria dos Conjuntos - Diagrama de Venn!
42 - x + x + 95 - x = 120
(...)
x = 17
-
Enquanto essa galera aí tá na fórmula, o japonesinho já tá em casa corrigindo a prova!
-
que fórmula o que....
Para intersecção, soma tudo e tira o total
95+42=137
137-120=17 !
fácil?
-
fui pelas alternativas T.T
Indo pelas alternativas... a letra B, ou seja, valor 17 subtraído de 42 e 95, resulta em: 25 e 78, respectivamente.
Depois, a somatória do 17 + 25 + 78: 120, o total de funcionários.
não sabia o macete da para encontrar sem fórmulas, bem mais simples :|
-
120 (total) - 95 (VR) = 25
42(VT) - os 25 que sobrou = 17 que recebem ambos os benefícios.
-
Essa foi para não zerar a prova de raciocínio lógico!
-
120 = Total de Funcionários
42 = VT = Y
95 = VR = Z
Quem recebe ambos = X
y + x + Z = 120 >> Total de funcionários
y + x = 42 >> Todos os que recebem apenas o VT + os que recebem os dois.
x + z = 95 >> Todos os que recebem apenas o VR + os que recebem os dois.
y + x + z = 120
42 + z = 120
z = 78
x + z = 95
x + 78 = 95
x = 17
y + x + z = 120
y = 120 - 78 - 17
y = 25
Gab.: B
-
total de funcionário: 120
VT=42
VL=95 +
----------
137
137-
120
------
17 --> TOTAL QUE RECEBEM AMBOS BENEFÍCIOS
-
Método Telles.
-
-
deu até medo de responder
-
Repare que temos 2 conjuntos de funcionários: os que recebem vale-transporte e os que recebem vale-refeição. Queremos saber justamente o número de elementos na INTERSEÇÃO, ou seja, os funcionários que recebem os dois benefícios.
Quando temos 2 conjuntos e pretendemos calcular o número de elementos na INTERSEÇÃO, basta fazermos:
Interseção = Soma dos conjuntos – Total
Isto é,
Interseção = (42 + 95) – 120
Interseção = 137 – 120
Interseção = 17
Rápido, não? Este é o “macete” que você pode utilizar nas questões com 2 conjuntos cujo objetivo é obter a interseção.
Vamos trabalhar os demais métodos?
Sejam A e B os conjuntos de pessoas que recebem vale-transporte e vale-refeição, respectivamente. O enunciado nos informa que n(A) = 42 e n(B) = 95. Como todos os funcionários recebem ao menos um desses benefícios, a união dos dois conjuntos é de 120 funcionários, ou seja, n(A U B) = 120. Podemos jogar tudo isso na fórmula para dois conjuntos:
n(A U B) = n(A) + n(B) – n(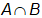
)
120 = 42 + 95 – n(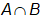
)
n(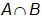
) = 137 – 120
n (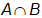
) = 17
Portanto, 17 funcionários recebem ambos os benefícios.
Vamos resolver agora com diagramas? Basta desenhar os 2 conjuntos entrelaçados:
Feito isso, devemos começar preenchendo a região de interseção. Como a questão não dá o valor da interseção (é justamente ele que queremos encontrar), colocamos uma variável (X) para então dar sequência ao preenchimento. Sabemos que 42 elementos fazem parte do conjunto A e, destes, X também fazem parte de B. Logo, os elementos que fazem parte SOMENTE de A são 42 – X. Também sabemos que 95 elementos fazem parte de B e, destes, X também fazem parte de A. Deste modo, os elementos que fazem parte SOMENTE de B são 95 – X. Colocando isso no diagrama:
Para sabermos o valor de X, basta somar todas as regiões do gráfico e igualar ao total (120), ficando com:
120 = 42 – X + X + 95 – X
120 = 137 – X
X = 17
Resposta: B
-
Tão simples que chega a dar medo! Mas não podemos subestimar nosso conhecimento...às vezes, por achar tão simples e pensar que pode ser pegadinha, acaba deixando de somar ponto pela falta de confiança!
-
Se todos recebem ao menos um auxílio, então somamos os que recebem transporte com os que recebem refeição, ou seja, 42 + 95 = 137; Esse número excede os 120 funcionários. Logo, o excedente, ou seja 137 - 120 = 17, são os funcionários que recebem dois auxílios.
-
Gabarito:B
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!