-
Olá Anderson, neste caso você não utiliza o PFC, pois a ordem DA ESCOLHA DO PRESO (OUTROS CRIMES) NÃO IMPORTA.
É só utilizar Combinação.
C (140,2) = 140! / 2! (140 - 2)
140! / 2! (138)!
140 * 139 / 2
19.460 / 2 = 9730
RESPOSTA CERTA.
-
Sou professor de Matemática, e posso afirmar que o resultado é obtido através de uma combinação.
O colega acima está corretíssimo em sua análise, o resultado é 9730, então a resposta está certa.
-
Qualquer tipo de exercicio desse tipo pode ser feito utilizando-se o PFC.
Porem, em casos em que a ordem dos elementos nao altera o resultado, deve-se excluir os casos em que os 2 elementos se repetem.
Nesse caso deve-se dividir por 2. Como exemplo podemos citar o caso do preso "1" e o preso "2" serem escolhidos. Isso nao seria diferente se o "2" fosse escolhido primeiro e em seguida o "1".
Ou seja, o calculo do amigo Anderson esta correto, só faltou eliminar os casos repetidos dividindo o resultado dele por 2.
-
Primeiro, vamos representar a distribuição dos presos, sabendo que alguns estavam presos por roubo e homicídio:
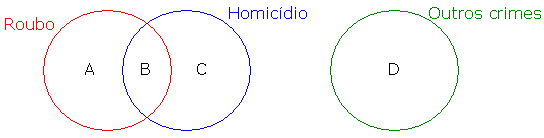
Sabemos ainda que:
O presídio continha 420 detentos
A + B + C + D = 420 (equação 1)
140 foram condenados por outros crimes
D = 140 (equação 2)
210 foram condenados por roubo
A + B = 210 (equação 3)
140 foram condenados por homicídio
B + C = 140 (equação 4)
Substituindo os valores de D e de A + B das equações 2 e 3 na equação 1, temos:
A + B + C + D = 420
210 + C + 140 = 420
C = 420 – 210 – 140
C = 70
Substituindo o valor de C na equação 4, temos:
B + C = 140
B + 70 = 140
B = 140 – 70
B = 70
Substituindo o valor de B na equação 3, temos:
A + B = 210
A + 70 = 210
A = 210 – 70
A = 140
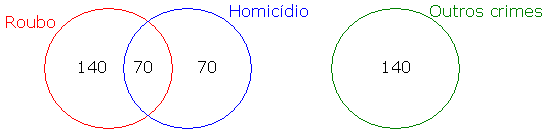
Agora, para selecionar dois detentos entre os condenados por outros crimes, podemos entender que formaremos um grupo de 2 pessoas entre os 140 disponíveis, onde a ordem da escolha não importa. Com isso, utilizaremos a combinação dos 140 detentos, dois a dois:
C(140, 2) = (140!)/[2!.(140-2)!] = (140.139.138!)/[2.(138)!] = (140.139)/[2] = 70.139 = 9730
-
Tem gente complicando. Lembrem-se sempre do tempo e do cansaço mental na hora da prova.
Neste item utiliza-se Combinação na quantidade de presos por Outros Crimes (140)
DICA DE COMBINAÇÃO
C(x,y) = x desce y vezes multiplicando (sem fatorial) / y! (com fatorial)
Exemplo:
C (4,2) = 4x3/2! = 4x3/2 = 12/2 = 6
C (6,3) = 6x5x4/3! = 6x5x4/3x2 (corta 6 com 3x2) = 5x4 = 20
C (10, 5) 10x9x8x7x6 / 5! = 10x9x8x7x6 / 5x4x3x2 = 252
Explicando:
C(4,2) = O 4 multiplica 2 vezes de forma decrescente, assim fica: 4x3 / 2!
C(6,3) = O 6 multiplica 3 vezes de forma decrescente, assim fica: 6x5x4 / 3!
C (10,5) = O 10 multiplica 5 vezes descrescendo e o 5 vem embaixo com fatorial: 10x9x8x7x6 / 5!
Resolvendo a questão com a DICA:
C (140,2) = 140x139 / 2! (O 140 multiplica 2 vezes descrescendo)
19460 / 2 = 9730
CERTO.
Sei que é complicado explicar por aqui, mas pra quem entender isso agiliza e muito nossa vida com combinação na prova. Economiza tempo e trabalha menos com fórmula. Espero ter ajudado.
Abraço.
-
Segundo o Prof Arthur Lima do Estratégia a questão é resolvida por meio da Combinação mesmo
C(140,2)= 140x139/2 = 9730
-
Galerinha, tem gente passando o BIZU errado!!! Galera, vamos ter consideração e só "ensinar" quando tiver certeza!!!!!
-
Uma dúvida!!!
O enunciado pede a quantidade de maneiras distintas de selecionar 02 detentos.
Nesse caso a ordem importa porque AB é diferente de BA?
Então se a ordem importa, lembrando que o enunciado pede de "maneira distinta", devemos considerar permutação e não combinação.
Alguém poderia me auxiliar?
Bons estudos
-
forma simples de fazer sem fórmula. ..
se vai escolher 2 detentos dentro do 140... entao vamos lá:
pfc
140 x 139 / 2!
140 primeira possibilidade, 139 na segunda possibilidade.. 2! pq tanto faz eu ter escolhido zezinho e luizinho ou luizinho e zezinho.. São mesmo grupo...por isso divide-se 2!
resultado 9730.
-
Inicialmente errei a questão, mas o problema do enunciado está na interpretação. Perceba que ele quer selecionar 2 detentos para um outro grupo, um programa destinado à ressocialização. É um combinação.
Matemática no Cespe é como jogar 14 erros.
-
Por que a ordem não importa?
-
Alguem mais acha que esta questão cabe recurso de ANULAÇÃO?
Vejam meu raciocínio:
1) Temos então 3 conjuntos: R, H e O, sendo estes os conjuntos formados pelos detentos presos por Roubo, Homicídio e Outros crimes, respectivamente.
2) Pela senteça "Verificou-se, também, que alguns estavam presos por roubo e homicídio", conclui-se que a interseção dos Conjuntos R e H é NÃO VAZIO, ou seja existem elementos em comum;
3) O enunciado afirma que 140 detentos cometeram outros crimes. Mas não deixa claro que cometeram APENAS outros crimes. Logo, a interção dos conjuntos O e R, bem como dos conjuntos O e H, PODE (e pode sim, pelo enunciado) ser também não Vazio.
Chega-se fácil ao gabarito considerando que os 140 cometeram apenas outros crimes, OK... Mas que ela cabe recurso de anulação, cabe. Pois tal consideração é uma extrapolação.
-
1º passo : a questão só pediu os detentos que cometeram outros crimes (140)
2º passo: quero selecionar 2 entre os 140, então faço 140x139= 19.460, esse valor é a quantidade de maneiras distintas de eu selecionar 2 detentos.
3º passo: divido por fatorial de 2, pois entre eles pode mudar a ordem. Explico: digamos que entre os 140 foram escolhidos A e B, mas quem disse que essa seria a ordem? Poderia ser B e A, portanto fatorial de 2.
4º passo: depois que dividiu 19.460 por 2 ache o resultado de 9.730 que é inferior a 10.000.
Gabarito C
-
C= 140*139= 19460/2 = 9730.
gabarito correto.
-
A questão falou sobre a A quantidade de maneiras distintas, nesse caso a ordem importa, Não seria correto utilizar Permutação ..alguém explica ??
-
* Arranjo: Quando posso ESCOLHER. A ordem importa.
Quando uso? Em geral na formação de números, senhas, protocolos, placas, etc.
Resolve-se pelo princípio multiplicativo.
* Combinação: Quando posso ESCOLHER. A ordem não importa.
Quando uso? Formação de grupos, times, equipes, comissões.
Resolve-se pela fórmula: C= n! / p! (n-p)!
* Permutação: VOCÊ NÃO ESCOLHE NADA! Você embaralha o que você tem.
Quando uso? Formação de filas, anagramas, etc.
Resolve-se pela fórmula: P = n!
-
Vale lembrar que caso a questão especificasse alguma diferença entre os 2 detentos selecionados(p. ex, um para fazer uma função e outro outra), a ordem importaria, e aí a questão mudaria para arranjo
-
Item: Correto.
C 140, 2 = 9730.
Bons estudos!
-
C 140,2
140!
2!* 138! = 9730
QUESTÃO CORRETA!
-
CERTO
Combinação.
140.139/2.1 = 19460/2 = 9730