Questão 746587

• Banca: ESAF
• Órgão: CGU
• Ano: 2012
• Provas: ESAF - 2012 - CGU - Analista de Finanças e Controle - prova 1 - Conhecimentos gerais
• Disciplina: Raciocínio Lógico
• Assuntos: Raciocínio Matemático

Um segmento de reta de tamanho unitário é dividido em duas partes com comprimentos x e 1-x respectivamente. Calcule o valor mais próximo de x de maneira que

x = (1-x) / x, usando = √5 ≅ 2,24

• A. 0,62
  
• B. 0,38
  
• C. 1,62
  
• D. 0,5
  
• E. 1/ π

Gabarito: A

Comentários

• x=(1-x)/x
  x^2 + x - 1 = 0
  
  Usando a famosa fórmula de Baskara:
  
  
  
  -b = -1
  Delta = b^2 - 4ac = 5
  2a = 2
  
  x =( -1 + 2,24)/ 2 = 0,62
  x = ( -1 -2,24)/2 = -1,62
  
  X não pode ser negativo pois é um segmento de reta, então o único valor possível é 0,62.
  
• Não tinha um jeito mais dinâmico de fazer isso não??
• Pode-se testar as alternativas. Ao confirmar a primeira, eu já havia dado a questão por encerrada.
  
  a) 0,62     ->     x = (1-x) / x  =>  0,62 = (1-0,62) / 0,62 => 0,62 = 0,62 Verdadeiro
  b) 0,38     ->     x = (1-x) / x  =>  0,38 = (1-0,38) / 0,38 => 038 = 1,62 Falso
  c) 1,62     ->     x = (1-x) / x  =>  1,62 = (1-1,62) / 1,62 => 1,62 = 0,38 Falso
  d) 0,5       ->     x = (1-x) / x  =>  0,5 = (1-0,5) / 0,5 => 0,5 = 1 Falso
  e) 1/n       ->     x = (1-x) / x  =>  1/n = (1-(1/n)) / (1/n) => 1/n = n-1 Falso
  
  Boa sorte!
• Felipe, como assim????... Alguem pode me ajudar a entender.
  
  A formula antes disso, tambem não entendi.
  
  bahhhh ((((

• A questão se baseia no conhecimento da proporção áurea (https://pt.wikipedia.org/wiki/Propor%C3%A7%C3%A3o_%C3%A1urea). A forma de resolver é essa que o pessoal apresentou mesmo, através de Báskara. Apesar de ser da wikipedia, a explicação está certa e é bem interessante.

• Partimos da igualdade dada no enunciado:

  x = (1 – x) / x

  x = 1 – x

  x + x – 1 = 0

  

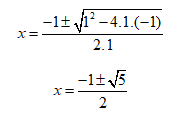
                 Usando a aproximação dada no enunciado (√5 ≅ 2,24), temos:

  

  x = -1,62 ou  x = 0,62

                 Dessas duas opções para x, devemos considerar o valor positivo (isto é,  x = 0,62), pois a medida de um segmento deve ser sempre um número positivo.

  Resposta: A

• Sabemos que x = (1 - x) / x.

  O x que está dividindo passa para o outro lado multiplicando, então:

  x . x = (1 - x)

  x^2 = 1 - x

  observe que temos uma equação do segundo grau. Passando tudo do lado direito para o esquerdo, fica da seguinte forma a equação:

  x^2 + x - 1 = 0

  a = 1

  b = 1

  c = -1

  b^2 - 4.a.c

  1 - 4. 1. (-1)

  1 + 4 = 5

  Para encontrar o valor de x:

  x = (-b+ou- raiz quadrada de 5) / 2. a

  x = (-1 + ou - 2,24) / 2

  x' = (-1 + 2,24)/ 2 = 0,62

  x" = (-1 - 2,24)/2 = -1,62