-
Djanilson
Perfeito o seu comentário, mas com uma observação, na parte de baixa que esta escrito a caneta você colocou o gabarito como letra D.
Mas mesmo assim ficou bem claro a sua explicação.
-
Nesta questão analise as porposições a medida que aparecem na questão, daí a primeira proposição sobre a pessoa assume o valor de verdade, as seguintes serão, em regra, falsas. Embora nada impessa que um pessoa tenha mais de uma profisão, o que não deve ser levado em consideração.
-

-
Não entendi... pois não consigo fechar todas as premissas com valor V
ou não precisa?
-
Repondendo passo a passo
1º Passo: você deve conhecer as regras. Veja as regras no comentário acima.
2º Passo: Agora que você já conhece as regras, vamos respondê-las
Importante lembrar que todas as proposições devem ter valor lógico VERDADEIRO.
Para encontrar a resposta temos que testar algumas hipóteses até encontrar a que preencha todos os requisitos da regra
1.Se Anamara é médica, então Angélica é médica.=VERDADEIRO (Para ter valor lógico verdadeiro a Vera(verdade) Fischer(falso) não poderá aparecer)
1. V V
2. F F
3. F V
2.Se Anamara é arquiteta, então Angélica ou Andrea são médicas.=VERDADEIRO
1. F V V - Para ser falso Todos devem ser falsos
2. V F V - Opa!!! A segunda sentença deu falso e a VF apareceu, então descarta essa hipótese
3. V V F - Aqui também ocorreu o mesmo problema da 2º hipótese, também devemos descartá-la
Nem precisaria fazer o resto, mas vou colocar pra questão ficar completa :D
3.Se Andrea é arquiteta, então Angélica é arquiteta.=VERDADEIRO
1. F F
2.
3.
4.Se Andrea é médica, então Anamara é médica.=VERDADEIRO
1. V V
2.
3.
Espero ter ajudado
Bons estudos
=D
-
p1 = A então B
p2 = -A então(B V C)
p3 = -C então -B
p4 = C então A
se pegar C=verdadeiro para p4 = verdadeiro A=vedadeiro
e assim por diante fazendo p1=v e p2=v e p3=v, se njão dar vedadeiro nas proposições então C não seria vedadeiro!!
acho que pode ser assim, também!!!!!!!
-
| ANAMARA MÉDICA = A | ANAMARA ARQUITETA = ~A |
| ANGÉLICA MÉDICA = B | ANGÉLICA ARQUITETA= ~B |
| ANDRÉIA MÉDICA =C | ANDRÉIA ARQUITETA = ~C |
| Se Anamara é médica, então Angélica é médica. | A --->B |
| Se Anamara é arquiteta, então Angélica ou Andrea são médicas | ~A--->[BvC] |
| Se Andrea é arquiteta, então Angélica é arquiteta. | ~C --->~B |
| Se Andrea é médica, então Anamara é médica | C --->A
|
| (v)A --->B(v) | PRIMEIRO ADMITAMOS QUE PROPOSIÇÃO “A” SEJA VERDADEIRA; “~A” SERÁ FALSA. SE “A” É VERDADE “B” TERÁ QUE SER VERDADE. POIS, (V F) DÁ FALSA. SE “B” É VERDADEIRO “~B” SERÁ FALSO. E, CONSEQUENTEMENTE “~c” TERÁ QUE SER FALSO, BEM COMO, “C” VERDADEIRO.
|
| (f)~A ---> [(v)BvC(v)] |
| (f)~C--->~B(f) |
| (v)C---> A (v) |
| |
| GABARITO LETRA "C" : (v)A,B(v),(v)C |
-
P | Q | P-->Q| P-->Q = Só sera falsa se P é verdadeira e Q é falsa.
V V V
V F F
F V V
F F V
I - Se Anamara é médica, então Angélica é médica.
II - Se Anamara é arquiteta, então Angélica ou Andrea são médicas.
III - Se Andrea é arquiteta, então Angélica é arquiteta.
IV - Se Andrea é médica, então Anamara é médica.
Anamara é medica = A1
Angelica é médica = A2
Andreia é médica = A3
I - A1-->A2
II - ~A1-->A2\/A3
III - ~A3-->~A2
IV - A3-->A1
Como essa questão não tem uma proposição simples ( o que facilitaria nossa vida ), o que temos que fazer é arriscar um palpite, por exemplo se A1 é falso ou verdadeiro. Arriscando que A1 é verdadeira e analisando conforme o quadro das verdades, chegaremos as conclusões que A1, A2 e A3 são verdadeiras.
Logo a letra C é a correta
c) Anamara, Angélica e Andrea são médicas.
-
Eu parto do princípio que todas as proporções são verdadeiras:
Se Anamara é médica, então Angélica é médica. ( V )
( V ) ( V )
Se Anamara é arquiteta, então Angélica ou Andrea são médicas. ( V )
( F ) ( F )
Se Andrea é arquiteta, então Angélica é arquiteta. ( V )
( F ) tenho que manter o valor de verdade então: ( F )
Se Andrea é médica, então Anamara é médica. ( V )
( V ) ( V )
Começo resolvendo da última afirmação:
Observação: faço a tradução literária da tabela verdade:
Anamara é médica.
Angélica é médica.
Andréia é médica.
Nenhuma das três é arquiteta.
Resposta letra: C
Lembrete: A condicional para ser falsa a primeira afirmação tem que ser verdadeira e a segunda falsa, como eu parto do principio que todas são verdadeiras pra não ser falsa eu não uso o chamado Vera F ischer.
-
Para resolver esta questão, deve-se, primeiramente, conhecer e dominar as tabelinhas das proposições, logo, você, nesta questão, sempre chegará à conclusão que nenhuma poderia de arquiteta.
-
Letra C
.
.
Não sei o que aconteceu, mas APAGARAM VÁRIOS dos meus comentários (de matemática e raciocínio lógico) aqui no QC.
É foda mesmo, porém vou colocá-los de volta pois sei que ajuda/ajudou a muitos.
Bons estudos para todos nós! Sempre!
-
Colegas, segue um passo a passo de como resolvi a questão.
P1 = Se Anamara é médica, então Angélica é médica
P2 = Se Anamara é arquiteta, então Angélica ou Andrea são médicas
P3 = Se Andrea é arquiteta, então Angélica é arquiteta.
P4 = Se Andrea é médica, então Anamara é médica.
Passo 1: Notei que todas as 4 proposições possuem uma condicional. Para isto é fundamental que saibamos sua tabela verdade, ou seu conceito que diz que a proposição só terá valor falso se a primeira for verdade e a segunda for falsa.
Passo 2: Como não há nada definido, comecei pela P1 e assumi que "p" (Anamara é médica) é verdade, logo "q" (Angélica é médica) obrigatoriamente terá de ser verdade, caso contrário a (p->q) terá valor falso.
Já sei que Anamara é médica e Angélica é médica.
Passo 3: Procuro outra proposição que envolva Angélica e Anamara e que possua apenas o conectivo condicional.
Assim, passo para P4, e anoto que "q" (Anamara é médica) é uma verdade, mas não tenho ainda como afirmar se "p" (Andrea é médica) é verdade ou mentira, pois seja verdadeira ou falsa, a (p->q) terá valor Verdadeiro
Passo 4: Sigo na próxima proposição que tenha apenas um conectivo condicional. Em P3 noto que "q" (Angélica é arquiteta) é falso, pois sei que Angélica é médica. Desta forma para que P3 tenha valor verdadeiro "p" (Andrea é arquiteta) obrigatoriamente será falsa.
Aqui descubro que Andrea é médica.
Passo 5: Retorno para a P4, vista no passo 3, e com base na anterior anoto que "p" (Andrea é médica) é verdade. Assim (p->q) terá valor verdadeiro.
Passo 6: Já sei que as 3 são médicas, mas me falta uma proposição para confirmar. Em P2 temos uma condicional e uma disjunção. Chamarei de p->(q v r). Resolvendo primeiro a disjunção, com base no que sabemos, teremos "q" (Angélica é médica) Verdadeiro e "r" (Andrea é médica) Verdadeiro. Conhecendo a tabela verdade de uma disjunção, sabemos que ela só terá valor falso se ambas forem falsas. Como ambas são verdades, ela tem valor verdadeiro. Voltando a condicional temos "p" (Anamara é arquiteta) que é falsa, logo p->(q v r) terá se confirmado como verdadeira pois a primeira é Falsa e a segunda Verdadeira, desta forma P2 tem valor verdadeiro.
Questão resolvida. Resposta letra C.
Obs: poderia ter partido supondo que Anamara é arquiteta, e não médica, mas em algum momento teria uma preposição com valor Falso, contrariando o enunciado da questão,
Espero ter ajudado e sido claro, apesar de usar apenas palavras.
-
| P | Anamara médica | → | Q | Angélica médica | | | |
| ¬P | Anamara arquiteta | → | Q | Angélica médica | V (ou) | R | Andrea médica |
| ¬R | Andrea arquiteta | → | ¬Q | Angélica arquiteta | | | |
| R | Andrea médica | → | P | Anamara médica | | | |
P → Q ≡ V → V = V
¬P → (Q v R) ≡ F → (V ou V) = V
¬R → ¬Q ≡ F → F = V
R → P ≡ V → V = V
-
Para resolver este tipo de questão, a maneira mais rápida é a seguinte:
1) Escreva as proposições, conforme a ordem do enunciado;
P = Anamara é médica;
Q = Angélica é médica;
R = Anamara é arquiteta;
S = Andrea é médica;
T = Andrea é arquiteta;
U = Angélica é arquiteta.
2) Transcreva em operações lógicas as afirmações do enunciado:
I) "Se Anamara é médica, então Angélica é médica" P->Q
II) "Se Anamara é arquiteta, então Angélica ou Andrea são médicas" R->(Q ou S)
III) "Se Andrea é arquiteta, então Angélica é arquiteta" T->U
IV) "Se Andrea é médica, então Anamara é médica" S->P
3) Procure por alguma relação entre as proposições e reescreva as afirmações do item 2 (se possível):
Neste caso podemos supor que "ser médica" e "ser arquiteta" são mutualmente excludentes, ou seja, quem é médica não é arquiteta e vice-versa. Desta forma temos as seguintes relações entre as proposições:
P = ~R
Q = ~U
S = ~T
Reescrevendo agora as afirmações do item 2 utilizando estas relações temos:
I) P->Q
II) ~P -> (Q ou S)
III) ~S -> ~Q
IV) S -> P
Note que agora temos 3 variáveis (e não mais 6 como inicialmente). E escrevi tudo em termo de "ser médica", para facilitar o item seguinte.
4) Agora com poucas variáveis, teste as alternativas (é mais rápido do que parece):
a) "Anamara, Angélica e Andrea são arquitetas" P=Q=S= Falso
I) Condição satisfeita
II) NÃO satisfeita
b) "Anamara é médica, mas Angélica e Andrea são arquitetas" P=Verdadeiro, Q=S=Falso
I) NÃO satisfeita
c) "Anamara, Angélica e Andrea são médicas" P=Q=S=Verdadeiro
I) Condição satisfeita
II) Condição satisfeita
III) Condição satisfeita
IV) Condição satisfeita
Logo, a alternatica C é a correta.
-
Inicialmente,
extraí-se das declarações do enunciado as proposições simples que compõem as
proposições compostas.
p, “Anamara é médica” ~p, “Anamara é
arquiteta”
q, “Angélica é médica” ~q, “Angélica é arquiteta”
r, “Andrea é médica” ~r, “Andrea é arquiteta”
Pode-se
então representar as proposições compostas do enunciado da seguinte forma:
a) “Se Anamara é médica, então
Angélica é médica.” p→q
b) “Se Anamara é arquiteta, então
Angélica ou Andrea são médicas.” ~p→(qvr)
c) “Se Andrea é arquiteta, então
Angélica é arquiteta.”
~r→~q
d) “Se Andrea é médica, então
Anamara é médica.” r→p
O candidato deve recordar que
para uma condicional (p→q) possuir valor FALSO, a primeira proposição tem que
possuir valor VERDADE e a segunda, FALSO.
Este fato pode ser verificado
através da Tabela-Verdade:
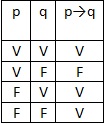
De acordo com o enunciado, todas
as proposições compostas são VERDADEIRAS. Analisando-as, tem-se:
a) “Se Anamara é médica (V),
então Angélica é médica(V).” p→q (V)
b) “Se Anamara é arquiteta (F),
então Angélica ou Andrea são médicas. (V) ” ~p→(qvr)
(V)
c) “Se Andrea é arquiteta (F),
então Angélica é arquiteta. (F)”
~r→~q (V)
d) “Se Andrea é médica (V), então
Anamara é médica. (V)” r→p (V)
Atendendo
a imposição do enunciado, verifica-se que nas proposições simples com valor
VERDADE, todas as três mulheres são médicas.
Resposta C)
-
são dois tipos de questões parecidas
no primeiro tipo (mais fácil) o execício fornece uma verdade ao final com uma frase do tipo: "-ora, anamara é médica"
no segundo tipo (mais difícil) o execício não fornece uma verdade conhecida, que é o caso deste exercício aqui
o macete rápido pra resolver sem tabelas, formulas e nada mais é fazer um teste
começo de preferencia pela ultima frase e assumo ela como verdadeira:
-Se Andrea é médica, então Anamara é médica (vou assumir que seja verdade e andrea é médica)
então anamara é médica
-Se Anamara é médica, então Angélica é médica
então angélica é médica também
-Se Anamara é arquiteta, então Angélica ou Andrea são médicas.
não é verdade que anamara seja arquiteta então esta frase não interessa
-Se Andrea é arquiteta, então Angélica é arquiteta.
andréa não é arquiteta então esta frase também não interessa
chegamos ao final sem nenhuma contradição então tudo o que foi dito é verdade
andréa, anamara e angelica são médicas
marquei a alternativa C sem nem olhar para as outras
-
nossa, questão quebrou minha cabeça... Fui pelo caminho mais difícil.
-
O texto deveria indicar que nenhuma delas é profissional de mais de uma área (cada uma ou é médica ou é arquiteta).
-
Transcrevendo o enunciado:
Considerando que as afirmações são verdadeiras.
Se Anamara é médica, então Angélica é médica. Se Anamara é arquiteta,
então Angélica ou Andrea são médicas. Se Andrea é arquiteta, então
Angélica é arquiteta. Se Andrea é médica, então Anamara é médica.
Iremos
representar as proposições simples por letras minúsculas do alfabeto (
p, q ,r...) e as proposições compostas por letras maiúsculas( A, B,
C...)
p: Anamara é médica
q: Angélica é médica
r:Anamara é arquiteta
s: Andrea é médica
t: Andreia é arquiteta
u: Angélica é arquiteta
A: p --->q
B: r -->q v s
C: t--->u
D: s ---> p
Construindo a valoração da condicional, a título de representação X ---> Y ( Para resolvermos a questão devemos nos basear nela)
X Y X--->Y
V V V
V F F
F V V
F F V
Se todas as afirmativas condicionais são corretas devemos excluir a combinação da 2ª linha da tabela verdade. V F = F
Seguindo
Testando as assertivas
a) Anamara, Angélica e Andrea são arquitetas; Val(r)= V; Val(t)= V ; Val(u)=V
Depreende-se
Anamara, Angélica, Andrea não são médicas ; Val(p)=F; Val(q)= F; Val(s)= F
Testando
A: p --> q = F --> F = V (ok!)
B: r -->q v s = V --> F v F = F ( ops, errada!)
Passamos para a assertiva b)
Anamara é médica, mas Angélica e Andrea são arquitetas; Val(p) = V ; Val(t) = V ; Val(u)= V
Depreende-se
Anamara não é arquiteta, Angélica e Andrea não são arquitetas; VAl(q) = F ; Val(s)= F ; Val(r) = F
Testando
A: p-->q = V -->F ( ops, errada!)
Seguindo para a assertiva c)
Anamara, Angélica, Andrea são médicas ; Val(p) = V ; Val(q) = V ; Val(s)= V
Depreende-se
Anamara, Angélica, Andreaa não são arquitetas; Val( r) = F ; Val(t)= F; Val(u)= F
Testando
A: p ---> q = V --> V = V(ok!)
B: r -->q v s = F ( primeira falsa nem precisa testar o resto, tudo ok!)
C: t--->u = F --->F = V (ok!)
D: s --->p = V ---> V = V (ok!)
GABARITO C)
-
3 PESSOAS PARA 2 PROFISSÕES...
--> Ana é médica ou arquiteta.
--> Angélica é médica ou arquiteta.
--> Andrea é médica ou arquiteta.
SE A PESSOA É MÉDICA ENTÃO NÃO SERÁ ARQUITETA.
SE A PESSOA É ARQUITETA ENTÃO NÃO SERÁ MÉDICA.
TÍPICA QUESTÃO DA ESAF, TODA PROVA APARECE UMA IGUAL...
Parti para a resolução escolhendo uma premissa qualquer e atribuindo um valor lógico. Escolhi ''Ana.Arq. = FALSA''...sabendo que todas as proposições têm que ser verdadeiras, cheguei ao resultado solicitado. Observe abaixo.
Ana.Med --> Ang.Med = Verdadeiro
V --> V = Verdadeiro
Ana.Arq --> ( Ang.Med v And.Med) = Verdadeiro
F --> V v V
F --> V = Verdadeiro
And.Arq --> Ang.Arq = Verdadeiro
F --> F = Verdadeiro
And.Med --> Ana.Med = Verdadeiro
V --> V = Verdadeiro
GABARITO ''C''
-
Fiquei com dúvida na questão, pois a negação de ser médico não é necessariamente ser arquiteto e a questão não fala nada sobre as três mulheres terem somente uma profissão.
-
Mesmo quem não sabe a tabela verdade pode resolver essa questão, basta analisar as proposições. Considerando que a questão afirmou que todas são verdadeiras.
A) Errada. Pois as três não podem ser médicas, uma vez que " Se Anamara é arquiteta, então Angélica ou Andrea são médicas"
B) Errada. Pois "Se Anamara é médica, então Angélica é médica"
C) Correta. Pois "Se Anamara é médica, então Angélica é médica" e " Se Andrea é médica, então Anamara é médica"
D) Errada. Pois " Se Anamara é médica, então Angélica é médica"
-
porque "ser médica" torna falso "ser arquiteta"?
obgda!
bons estudos!
-
Graça Lima:
Ou a pessoa é medica ou é arquiteta. Se é médica não é arquiteta.
-
Minha dúvida é: como posso afirmar a pessoa tem que ter somente uma profissão???
a questão não fala isso.
-
Carolzinha P:
Dentro do princípio do terceiro excluído: toda proposição só pode ser falsa ou verdadeira, excluindo-se qualquer outra hipótese. Dessa maneira, para raciocínio lógico, uma pessoa assume só uma condição: profissão, cor, estado. Se ela é médica não tem outra profissão. Por isso a afirmativa que a considera arquiteta é a negação da primeira afirmativa que a declara médica.
Anamara é médica = q (V)
Anamara é arquiteta = ~q (F)
Espero ter ajudado.
-
Resolução no Youtube: https://www.youtube.com/watch?v=tRTnBWCNblw. Passo a passo muito bom.
-
LP Valeu seu comentário!
-
A dica econtra-se nas alternativas de questões desse tipo, que não leva a dica no enunciado das questões.
-
FÉ!
-
é certo que o fato de ter uma profissão nao implica em não exercer a outr tbm;
porem, ao olhar as opçoes da questão, constata-se que não há prejuizo algum em considerrá-las excludentes, para fins de resolução da questão;
isso inclusivé é uma das técnicas de resolução de sentenças: considerar uma como verdadeira e outra como falsa
-
Pessoal eu resolvi essa questão no chute mesmo eu atribui que a Angélica é médica ai fui resovolvendo baseando na tabela verdade, considerando que na condicional só tem uma possibiidade de ser falsa V F
-
Primeiro ler as alternativas para depois analisar as proposições do enunciado.
Estas duas proposições resolvem a Questão:
-> Se Andrea é médica, então Anamara é médica.
-> Se Anamara é médica, então Angélica é médica.
Como todas as afirmações são verdadeiras, aplicando estas frases nas opções, a única alternativa plausível é de que Todas são Médicas.
-
Temos as premissas abaixo, todas elas proposições compostas:
P1: Se Anamara é médica, então Angélica é médica.
P2: Se Anamara é arquiteta, então Angélica ou Andrea são médicas.
P3: Se Andrea é arquiteta, então Angélica é arquiteta.
P4: Se Andrea é médica, então Anamara é médica.
Já as alternativas de resposta são proposições simples. Assim, devemos usar o método do “chute”. Assumindo que Anamara é médica, em P1 vemos que Angélica é médica. Em P3 vemos que “Angélica é arquiteta” é F, de modo que “Andrea é arquiteta” tem que ser F, ou seja, Andrea não é arquiteta. Veja que P2 já é uma proposição verdadeira, pois como Angélica é médica, então “Angélica ou Andrea são médicas” é V. E note também que P4 já é uma proposição verdadeira, pois “Anamara é médica” é V. Assim, foi possível tornar as 4 premissas verdadeiras simultaneamente, o que permite concluir que Anamara é médica, Angélica é médica, e Andrea não é arquiteta.
Analisando as alternativas de resposta, vemos de cara que as opções A, B, D e E são falsas, pois nenhuma das três é arquiteta.
A alternativa C diz:
c) Anamara, Angélica e Andrea são médicas
Sabemos que Anamara e Angélica podem ser médicas, mas concluimos apenas que Andrea não é arquiteta. Não temos elementos para afirmar que Andrea é médica. A verdade é que o examinador queria que assumíssemos que só existem 2 profissões disponíveis: medicina ou arquitetura. Assim, como Andrea não é arquiteta, ela também tem que ser médica.
Resposta: C
ATENÇÃO: embora alunos tenham interposto recurso, esta questão não foi anulada pela banca. É importante ir pegando essa “malícia” para, na hora da prova, você marcar a alternativa “menos errada”, que neste caso era a letra C.