-
Regra de 3:
6 constroem 120 metros em 2 dias, portanto
6 constroem 60 metros em 1 dia, assim
1 constroi 10 metros em 1 dia, e
1 constroi 30 metros em 3 dias, daí
X constroem 210 metros em 3 dias:
X vezes 30 = 1 vezes 210
X = 210 / 30 = 7
-
Para construir 120 m2 de um muro em 2 dias, são necessários 6 pedreiros [então 6 pedreiros fazem 60 m² por dia (120/2)]. O número de pedreiros necessários para construir 210 m2 //se 6 pedreiros fazem 60 m² por dia, então 210 m² exigem 21 pedreiros=
6___60 m²
x___210 m²
60x = 1260
x = 21
desse mesmo muro em 3 dias é igual a. (21 pedreiros fazem 210 m² por dia. Como temos 3 dias p/ fazer 210 m²=> 21 pedr / 3 dias = 7
7 pedreiros fazem 210 m² em 3 dias.
-
Apenas usei o conceito de proporcionalidade. Daí, considerei:
n . d = k . t
sendo:
n: o número de pedreiros
d: o número de dias
t: o tamanho do muro
k: a constante de proporcionalidade (arbitrária)
Calculando, com os dados fornecidos, tem-se:
6 . 2 = k . 120
k = 1/10
Usando este valor de k para as condições pedidas, tem-se:
n . d = t / 10
n . 3 = 210 / 10
n = 7
-
Letra E
.
.
Não sei o que aconteceu, mas APAGARAM VÁRIOS dos meus comentários (de matemática e raciocínio lógico) aqui no QC.
É foda mesmo, porém vou colocá-los de volta pois sei que ajuda/ajudou a muitos.
-
Gab. E
120M - 2 Dias - 6 pedreiros
210M - 3 Dias - X
Para montar a regra de três é só dividir a linha de cima pela linha de baixo. Porém, tem que analisar as grandezas = se aumentar o número de pedreiros diminui a quantidade de dias => inversamente proporcional.=> inverte o numerador com o denominador => aqui fica 3/2.
Se aumentar a quantidade de pedreiros aumenta a área construída do muro => diretamente proporcional => mantém pois não precisa inverter nada => aqui fica 120/210 e 6/X
Fica assim: 120/210 x 3/2 = 6/X
120 x 3 x X = 6 x 210 x 2
360X = 2520
X = 252/36
X = 7
-
Esta questão requer
que o candidato demonstre conceito de Regra de Três Composta. É necessário
recordar a ideia de grandezas direta e inversamente proporcionais.
A quantidade de pedreiros e o
número de dias são grandezas inversamente proporcionais, pois quanto maior for
a quantidade de pedreiros usada, menor será o número de dias para construção do
muro.
Entretanto, a quantidade de
pedreiros e o tamanho do muro são grandezas diretamente proporcionais, pois
quanto maior for a quantidade de pedreiros usada, maior será o tamanho do muro
construído. Assim:
6 pedreiros
---------- 2 dias ---------- 120m²
X pedreiros
---------- 3 dias ---------- 210m²
6/X = (120/210) *
(3/2)
6/X = 360/420
360X = 2520
X = 7 pedreiros
Resposta E
-
120m---2 dias = 60m por dia
210m---3 dia = 70m por dia 60 esta para 6 pedreiros assim como 70 esta para.... 7 pedreiros
-
metros dias pedreiros
120 2 6
210 3 ?
6/x = 120/210 . 3/2
simplificando
6/x = 12/21 . 3/2
6/x = 6/7
6x= 6.7
6x = 42
x= 42/6 = 7 pedreiros
-
Podemos fazer da seguinte forma:
Em 1 dia - 6 pedreiros - 60 m² = 10 m²/pedreiro
Como o exercício diz "trabalhando no mesmo ritmo", entendemos que cada pedreiro não fará mais de 10 m²/pedreiro, então:
Em 1 dia - 7 pedreiros - 70 m² = 10 m²/pedreiro -- Logo:
Em 3 dias - 7 pedreiros - 210 m²
-
Obrigada, Djanilson!
-
Temos no enunciado 3 grandezas: área do muro, dias de construção, e número de pedreiros. Podemos resumir na tabela abaixo:
Área do muro Dias de construção Número de pedreiros
120 2 6
210 3 N
A variável que queremos descobrir está na coluna do número de pedreiros, portanto devemos verificar quais das outras variáveis são direta ou inversamente proporcionais a esta.
Para isto, basta pensar o seguinte: quanto MAIS pedreiros nós tivermos disponíveis, seremos capazes de construir MAIS muros e em MENOS dias. Portanto, observe que a variável “dias” é inversamente proporcional ao número de pedreiros, pois quando uma aumenta a outra diminui. Invertendo esta coluna, ficamos com:
Área do muro Dias de construção Número de pedreiros
120 3 6
210 2 N
Agora basta montar a nossa proporção, igualando a razão da coluna onde está a variável (N) com a multiplicação das demais colunas:
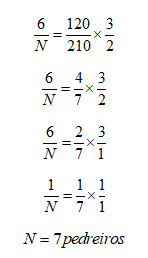
Resposta: E
-
MACETE: multiplicar os dois termos da mesma linha com o termo da parte superior e igualar com a multiplicação dos dois temos da mesma linha com o termo da parte inferior
120 - 2 - 6
210 - 3 - X
X . 3 . 120 = 6 . 2 . 210
X=7