-
Eminentes colegas,
As fórmulas de cálculo de eventos independentes conjugados são suficientes para resolver essa questão:
Considerando P(E1) a probabilidade de acontecer E1 e P(E2) a probabilidade de acontecer E2, tem-se:
P(E1 e E2) = P(E1) * P(E2) (a probabilidade de acontecer E1 e E2)
P(E1 ou E2) = P(E1) + P(E2) - P(E1 e E2) (a probabilidade de acontecer E1 ou E2)
Então:
P(E1) = a probabilidade de ser um processo que envolva autoridades influentes = 2/3 = 0,67 do total (dado fornecido pela questão)
P(E2) = a probabilidade de ser um processo que envolva desvio de altos valores = 3/5 = 0,6 do total (dado fornecido pela questão)
A quantidade de processos que envolverem, simultaneamente, autoridades influentes e desvios de altos valores:
P(E1 e E2) = 0,67 * 0,6 = 0,4 do total
A quantidade de processos não prioritários para análise é obtida da seguinte forma: calcula-se a quantidade de processos que tenham E1 OU E2 e subtrai-se do universo total:
P(E1 ou E2) = P(E1) + P(E2) - P(E1 e E2) = 0,67 + 0,6 - 0,4 = 0,87
Subtraindo-se o valor obtido acima do universo total (que é 1), tem-se: 1 - 0,87 = 0,13 do total
Portanto, errada a questão.
Saudações a todos.
-
http://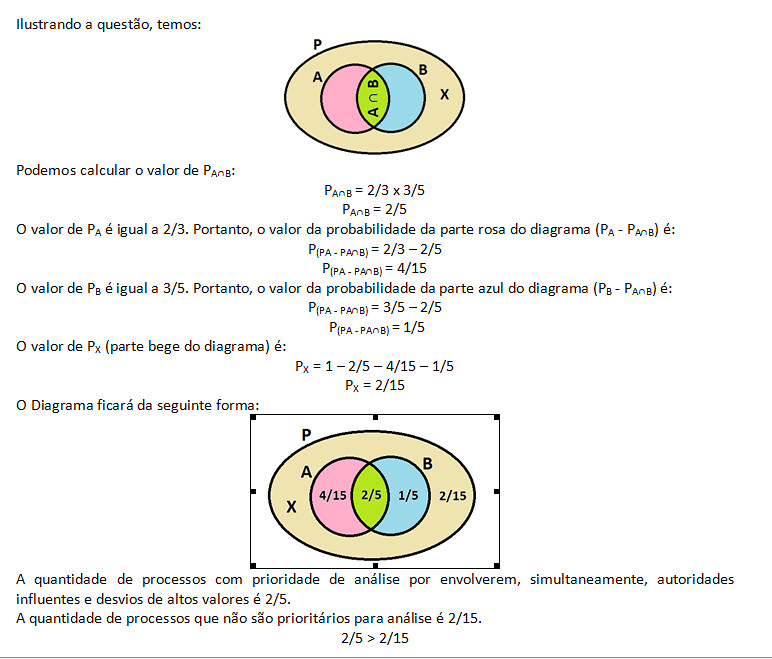
http://www.flickr.com/photos/77344121@N02/9239516515/
Gabarito: Errado
-
A 0 minutos atrás
Meu povo e minha pova são necessários 15 segundo para resolver essa questão.
Os processos de P que envolvem autoridades são 2/3 do total de processos - oras 2/3 é maior que 1/3. Nos resta concluir que os processos que envolvem pessoa influentes é em maior número do que todo o resto.
Portanto acertiva errada
-
Galera, não entendi os comentários dos colegas acima...
Não consegui visualizar qual o valor da interseção entre A e B.
Sem saber qual o valor da interseção, não há como saber qual o valor dos itens que não pertencem a A ou a B.
Considerando que P tem 15 elementos, A tem 10 e B, 9. Por isso, a interseção pode variar de 4 a 9 elementos. Enquanto os elementos que não pertencem a A ou a B podem variar de zero a 5 elementos.
Como a questão, na minha opinião, não forneceu dados para chegar a esses valores, é impossível concluir se os elementos que não pertencem a A ou a B são inferiores ou superiores a interseção entre A e B.
Se alguém quiser esclarecer como os colegas chegaram no valor da interseção, eu agradeço. Eles multiplicaram os valores dos percentuais de A e de B. Que regra é essa?
-
José Mario, mesmo tendo você, com seu racicínio, encontrado o gabarito da questão, não concordo com seu comentário. Pelo que você escreveu, a questão parece pedir a "união" dos processos de autoridades influentes e desvios de altos valores. No entanto, a questão pede a intersecção entre esses dois grupos. Note que o comando da questão é claro: "por envolverem, simultaneamente"... ou seja, ao mesmo tempo.
Creio que a maneira mais segura de se resolver tal questão seja da forma pela qual os amigos acima demonstraram...
-
Caro CICERO PEREIRA DE SOUZA, penso da mesma forma que você. Não entendi essa de multiplicar as probabilidades de A e B pra se chegar à interseção, e acho que isso está matematicamente errado.
Mas sobre o resultado da questão, pensei da seguinte maneira: em um dos casos extremos, de não haver processos que não sejam A nem B, ou seja, todos os processos ou são A ou são B, necessariamente, o número de processos que não são prioritários seria ZERO. Neste caso, ai sim, raciocinando como você falou, a interseção seria correspondente a 4/15, que é o valor MÍNIMO para a interseção. Partindo deste ponto, se formos incrementando o número de processos não são prioritários, de 0 em diante, podemos perceber que a cada incremento, o conjunto interseção vai necessariamente aumentando também, e daí caminhando neste sentido chegaríamos no OUTRO extremo, onde que teríamos o conjunto de não priorizados com 5/15 elemento e o conjunto interseção com 9/15 elementos.
O pulo do gato é perceber que NUNCA o conjunto de não priorizados vai ser maior que o conjunto interseção, pois num extremo eles serão respectivamente 0/15 e 4/15, e no outro extremo serão 5/15 e 9/15, OU SEJA, a frase da questão "a interseção é inferior à parte de não priorizados" NUNCA será verdadeira, o que torna a questão errada.
Se alguém concordar ou discordar, à vontade pra xingar, elogiar, se revoltar, me dar nota negativa, positiva, etc., mas vamos discutir a questão. :)
-
Para aqueles que estão com dúvidas de como calcular o valor da interseção, colocarei aqui algumas definições. Entretanto, se a dúvida persistir, recomendo pesquisarem sobre eventos independentes.
EVENTOS INDEPENDENTES
Dizemos que dois eventos são independentes quando a realização ou a não realização de um dos eventos não afeta a probabilidade da realização do outro e vice-versa. Por exemplo, quando lançamos dois dados, o resultado obtido em um deles independe do resultado obtido no outro.
Definição: A e B são eventos independentes se P (A ∩ B) = P (A) · P (B).
Material de apoio:
Eventos Independentes Bons Estudos!
-
Concordo plenamente com o Marcelo e com o Cícero. Não foi informado quantos processos NÃO prioritários existem em P, fração que pode variar de 0 a 1/3, dependendo da interseção entre A e B, que pode variar entre 4/15 e 9/15 de P.
Ainda, da mesma forma, na questão Q318382, "selecionando-se ao acaso um processo em trâmite na unidade em questão, a probabilidade de que ele não envolva autoridade influente será superior a 30%". Correto, varia de 66,67% a 100% (de 2/3 a 3/3), ou seja, considerando os números máximo e mínimo na interseção de A e B, como comentaram Marcelo e Cícero.
Não há que se falar em eventos independentes. Estamos falando de um único evento, retirar um único processo, que envolva A e B. Não estamos retirando dois processos do balaio, nem ao mesmo tempo, nem sucessivamente.
-
Pessoal, não precisamos desenvolver contas complexas ou raciocínios muito profundos para resolver a questão. Como o examinador não deu valores, basta atribuir um número qualquer para a quantidade de processos. Para facilitar nas contas, escolhi o 15. Dados: P = 15 (hipotético, poderia ser qualquer valor); P(A) = 2/3P; P(B) = 3/5P.
Resolução:
P = P(A) + P(B) *– P(simultaneamente A e B) + P(não prioritários)
15 = 10 + 9 – P(simultaneamente A e B) + P(não prioritários)
P(simultaneamente A e B) = 4 + P(não prioritários)
Ou seja, P(simultaneamente A e B) sempre será um número maior do que P(não prioritários), independente do valor de P. Gabarito: errado!
Simples assim! O examinador não quer saber os valores, mas sim quem é o menor entre os dois. Da próxima vez que ele perguntar algo parecido, levantem a hipótese de atribuir um valor à incógnita.
* Para quem não entendeu o “– P(simultaneamente A e B)”, P (A ∩ B) está incluso dentro do P(A) e do P(B), logo, devemos subtraí-lo uma vez para que não surja erroneamente dobrado na conta.
-
Dados:
(A ∩ B) = X
A=2/3
B=3/5
X= ?
Fórmula:
P(AUB) = P(A) + P(B) − P(A ∩ B)
Assumindo que P(AUB) equivale ao todo (100% dos processos prioritários) vamos considerá-lo como 1
1= 2/3 + 3/5 - X então X= 4/15
Agora temos as quatidades dos processos com prioridade
A=2/3
B=3/5
(A ∩ B) =4/15 (com prioridade simultânea) SUPERIOR
Automaticamente deduzimos que 11/15 são sem prioridade simultânea - INFERIOR
A quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores é inferior à de processos que não são prioritários para análise?
ERRADO.
-
O valor da intersecção que cheguei é 26,66% ou 4/15. No entanto, como a questão não dá o valor dos processos que não são prioritários para análise, então pode ser maior ou menor, não nos possilitando fazer afirmação alguma, portanto marquei a questão como errada.
-
Não tenho costume de fazer questão de raciocínio lógico. Na questão, não diz que os eventos de A e B são independentes, é de praxe o cespe deixar nas entrelinhas?
-
Aqui está bem explicado
https://www.youtube.com/watch?v=ChLiCqmckzI
-
-
P = prioritários + não prioritários
Suponha P = 15
A = 2/3x15 = 10
B = 3/5x15 = 9
Mas sabemos que tem uma interseção entre A e B = x
P = A + B + y (não prioritários)
(10 - x) + x (intersecção) + (9 - x) + y = 15
19 - x + y = 15
y = x - 4
y (não prioritário) será MENOR que x (intersecção)
-
2/3+3/5 = 5/8. Já diz tudo. Na prova tem de pensar rápido e lógico.
-
Fiz da seguinte forma, alguem puder responder se procede meu raciocinio.
Quem fica de fora é minoria, item E.
-
A QUESTAO NEM É TAO DIFICIL...O PANICO É QUE ATRAPALHA...CONTINUEM A LUTAR
-
li muitos comentarios, mas acho que os argumentos não justificam não. a questão esta errada pelo fato de não poder afirmar tal coisa dada a indeterminação da interseção.
-
As quantidades de processos envolvendo autoridades influentes e desvios de altos valores devem, necessariamente, satisfazer a seguinte relação:
n(P) = n(A) + n(B) – n(A∩B) + n(N)
Em que n(P) é a quantidade total de processos da unidade, n(A) é a quantidade de processos do conjunto A, n(B) é a quantidade de processos do conjunto (B), n(A∩B) é a quantidade de processos que simultaneamente pertencem ao conjunto A e ao B, e n(N) é igual à quantidade de processos que não são prioritários para a análise.
Sem perda de generalidade, vamos considerar que existam 15 processos na unidade. Nesta hipótese, teríamos:
n(P) = 15, n(A) = 10 (2/3 de 15), n(B) = 9 (3/5 de 15)
Assim, a relação entre as quantidades seria:
n(P) = n(A) + n(B) – n(A∩B) + n(N)
15 = 10 + 9 - n(A∩B) + n(N)
15 =19 - n(A∩B) + n(N)
n(A∩B) = 19 - 15 + n(N)
n(A∩B) = 4 + n(N)
O resultado indica que a quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores é 4 unidades maior do que à de processos que não são prioritários para a análise, ou seja, a quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores é superior à de processos que não são prioritários para a análise.
Gab.: ERRADO
Fonte: https://www.aprovaconcursos.com.br/noticias/2013/05/20/concurso-para-tecnico-mpu-2013-gabarito-comentado-da-prova-de-raciocinio-logico/
-
Fiz por MMC e acho que é uma boa...
(A) = 2/3(P) => 6/15 é o conjunto de processos envolvendo o alto escalão.
(B) = 3/5(P) => 9/15 é o conjunto de processos envolvendo desvio de dinheiro.
15 (total do conjunto P) - 9 (maior valor dos processos prioritários) = 6/15 (conjunto de processos que não possuem prioridade).
Percebam que a possibilidade do conjunto de processos envolvendo o alto escalão possuir completa interseção com a de processos envolvendo desvio de dinheiro é igual a do conjunto de processos que não possuem prioridade, portanto a afirmativa está incorreta.
-
Descomplicado:
A quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores é inferior à de processos que não são prioritários para análise.
autoridades influentes e desvios de altos valores processos que não são prioritários para análise.
2/3 + 3/5 =19/15 1/3+ 2/5 = 11/15
Gabarito errado, pois basta comparar as frações e concluir.
-
Essa resolução de multiplicar 2/3 e 3/5 esta errada.
A resolução postada por @Rafael Ferracioli é a correta
-
Seja P o total de processos. A quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores, é dada pelo número de elementos do conjunto  . A quantidade de processos prioritários é justamente a união entre A e B, ou seja, AUB. Assim, o total de processos não prioritários é P – n(AUB). Este item afirma que:
. A quantidade de processos prioritários é justamente a união entre A e B, ou seja, AUB. Assim, o total de processos não prioritários é P – n(AUB). Este item afirma que:

Por outro lado, note que o total de processos não prioritários é P – n(AUB). Assim, esse total será maior quanto menor for n(AUB). Como A tem 2/3 (66,6%) dos processos de B tem 3/5 (60%) dos processos, vemos que o menor número possível para n(AUB) é 2/3, que ocorre justamente quando o conjunto B está totalmente inserido no conjunto A (B é subconjunto de A). Assim, podemos dizer que:


Podemos agora avaliar a afirmação feita:

-
PARA QUEM NÃO ENTENDEU O PORQUE DO 15:
Ele simplesmente tirou o mmc dos denominadores, pois em números primos, o mmc dos denominadores é a multiplicação entre os termos.
-
A corresponde a 2/3 e B corresponde a 3/5. A questão fala que A e B acontecem simultaneamente, logo utilizaremos o princípio multiplicativo ( 2/3 x 3/5 = 6/15 que, simplificando por 3 dá 2/5). Os processos que não são prioritários correspondem a 3/5, que é maior que 2/5. Gabarito Errado.
-
Galera concurseira, achei uma forma de resolução muito tranquila!!
A questão é calma e pensamento crítico. Vamos lá!
Montem o diagrama de Venn e "dalhe"!
Autoridades / Intersecção / Valores
10 - y / y / 9 - y
Outros: X
Obs. Atribui o valor de 15 para tornar mais fácil o cálculo, recomendo!! haha
Parando pra pensar, podemos substituir o apenas Valores (9 - y) + X como 1/3, certo?
9 - y + x = 5
x = y - 4
Logo, podemos concluir que X (Outros processos) tem valor 4 unidades a menos que y (o valor de autoridades e valores). Sendo assim, a quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores é SUPERIOR à de processos que não são prioritários para análise. ERRADO
-
Temos que o total de processo é igual a P.
Escrevendo P como a soma das partes:
P=N(A)+N(B) - N(A∩B)+Cp(x)
Realizando as substituições N(A)=2P/3 e N(B)=3P/5
P=19P/15 - N(A∩B) + Cp(x)
Manipulando temos que:
N(A∩B)= 4P/15+Cp(x)
Temos que P não pode ser negativo, portanto N(A∩B)>Cp(x). logo questão ERRADA
-
A assertiva diz que n(A∩B) < n(P) - n(AUB).
Chamando n(P) de P (número de elementos no conjunto P), temos:
n(A∩B) < P - n(AUB)
Como n(AUB) = n(A) + n(B) - n(A∩B), temos que:
n(A∩B) < P - [n(A) + n(B) - n(A∩B)]
O texto nos disse que n(A) = 2P/3 e que n(B)=3P/5. Portanto,
n(A∩B) < P - [2P/3 + 3P/5 - n(A∩B)]
n(A∩B) < P - 2P/3 - 3P/5 + n(A∩B)
n(A∩B) < P - 19P/15 + n(A∩B)
Multiplicando a inequação por (-1):
-n(A∩B) > -P + 19P/15 - n(A∩B)
-n(A∩B) + n(A∩B) > -P + 19P/15 - n(A∩B) + n(A∩B)
0 > 4P/15
0 > P
Como P não pode ser inferior a 0, temos que a assertiva é falsa.
-
Parte 1
O conjunto P é o conjunto universo, ou seja, engloba todos os processos.
A = São os processos que dizem respeito a autoridades influentes e correspondem a 2/3 de P. (são prioritários).
B = São os processos que dizem respeito a altos valores e correspondem a 3/5 de P. (são prioritários).
C(A) é o complementar de A, ou seja, é o que existe no P que não é sobre A, ou seja, são 1/3 de P. (podem ou não ser prioritários).
C(B) é o complementar de B, ou seja, é o que existe no P que não é sobre B., ou seja são 2/5 de P. (podem ou não ser prioritários).
Temos 4 possibilidades dentro das possibilidades existentes de avaliar se os processos são prioritários:
1º - Ele pode ser de A e ser de B. (Logo, é prioritário).
2º - Ele pode ser de A e não ser de B. (Logo, ele é prioritário, já que pelo menos ele é de A).
3º - Ele pode não ser de A e ser de B. (Logo, ele é prioritário, já que pelo menos ele é de B).
4º- Ele pode não ser de A e não ser de B. (Logo, ele não é prioritário).
A pergunta que se faz é:
“A quantidade de processos com prioridade de análise por envolverem, simultaneamente, autoridades influentes e desvios de altos valores é inferior à de processos que não são prioritários para análise”.
Dentro das 4 possibilidades que temos, temos que avaliar se 1º< 4º.
Bom, vamos observar a 1º e a 4º possibilidade:
1º - Ele pode ser de A e ser de B. (Isso quer dizer que são os processos relacionados a A e a B ao mesmo tempo, em outras palavras, são os processos que trazem autoridades influentes juntamente com altos valores, ou vice-versa). Isso pode ser feito com a interseção entre eles. Portanto, seria o número de processão interrelacionados, ou seja, N(A Ⴖ B).
4º - Ele pode não ser de A e não ser de B. (Isso quer dizer que há processos que não se relacionam a A ou a B, ou seja, falam sobre outra coisa e que não foram marcados como prioritários). Logo, 4º = P – (1º + 2º + 3º). E o que seria essa (1º + 2º + 3º)? Seria a totalidade dos prioritários, quer seja, aqueles processos que tenham pelo menos A e B, ou ambos. Ou seja, (1º + 2º + 3º) = N (A U B). Portanto, 4º = P – N(A U B).
Agora que conseguimos representar tanto a 1º e a 4º possibilidade, vamos compará-las simbolicamente: E é exatamente isso que a banca quer.
1º → N(A Ⴖ B) < 4º → P – N(A U B) ?
Vamos trabalhar com números, só para exemplificar, e verificar se há verdade nessa afirmação.
-
Parte 2
Vamos supor que P possui 60 processos. (peguei esse número pois é múltiplo comum dos denominadores).
2/3 de P são de A = N(A) = 40 processos. (e são prioritários).
3/5 de P são de B = N(B) = 36 processos. (e são prioritários).
Apenas com esses números já ficamos com desconfiança sobre a veracidade da afirmação da banca, porém, ainda não somos completamente capazes de contradizê-la.
Vamos detalhar mais:
1/3 de P não são de A = C(A) = 20 processos (não sabemos se são ou não prioritários).
2/5 de P não são de B = C(B) = 24 processos (não sabemos se são ou não prioritários).
Qual a saída para essa situação? Como vamos saber distinguir cada processo? Impossível saber? Há uma forma de irmos aos extremos e avaliar as possibilidades, observe:
Olhe para essa pergunta: Até quantos processos prioritários eu posso ter ?
Os processos prioritários podem ir até 60, ou seja, pode haver 60 prioritários e nenhum processo não prioritário. Portanto, N(A U B) ≤ 60. Isso, não há como negar.
Lembremos da fórmula da União
N(A U B) = N(A) + N(B) - N(A Ⴖ B)
Portanto,
N(A U B) ≤ 60 → N(A) + N(B) - N(A Ⴖ B) ≤ 60
40 + 36 - N(A Ⴖ B) ≤ 60
76 - N(A Ⴖ B) ≤ 60
16 ≤ N(A Ⴖ B).
N(A Ⴖ B) ≥ 16. (1)
Agora, vamos observar a 4º possibilidade:
4º possibilidade = 60 – N(A Ⴖ B).
A 4º possibilidade (os não prioritários) será tanto maior quanto menor for N(A Ⴖ B).
Vamos ter que verificar o outro extremo. Observe que A possui 40 processos e B possui 36 processos. Qual dos dois possui o maior número de processos? O A né, rs. nisso você é bom, rs. Agora, diga-me: Qual dos dois pode comportar o menor número de processos prioritários possíveis? Acima, vimos o maior número de prioritários possíveis, agora, estamos avaliando o menor número de prioritários possíveis. Daí, você, sagaz, responde: Ah professor, são 36! Daí, eu te falo, 36? Não, na verdade, são 40.
-
Parte 3
Não se pode ter menos de 40, já que eu disse que 40 são prioritários, e por óbvio não pode haver menos que isso. E para reforçar ainda mais essa ideia, podemos inferir que todos os processos prioritários de B estão inseridos dentro dos prioritários de A.
Com essa ideia a gente pode fazer algumas afirmações.
60 - N(A U B) ≤ 60 – N(A)
60 - N(A U B) ≤ 60 – 40 ( pegamos da ideia acima, já que delimitamos em 40 processos o limite inferior, na verdade, temos: 40 ≤ N(A U B) ≤ 60).
60 - N(A U B) ≤ 20. (2)
Vamos agora voltar a pergunta da Banca:
1º< 4º? 1º = N(A Ⴖ B) < 4º = P – N(A U B) ?
Agora, finalmente, a gente consegue inferir algo. Vamos observar as equações (1), (2):
1º = N(A Ⴖ B) ≥ 16. (1)
4º = 60 - N(A U B) ≤ 20. (2)
Sejamos honestos, se eu tenho um número que é maior que 16 e eu tenho um número que é menor que 20, eu posso afirmar que o 1º é menor que o 4º? Claro que não né, basta apenas eu citar um simples exemplo: O número 21, ele é maior que que 16, e ainda por cima, é maior que 20. Logo, a banca mentiu pra você. A alternativa está errada.
-
Resolução da questão em 10min57s
https://www.youtube.com/watch?v=MuBgD7yjZp0
-
Podemos interpretar o ou como inclusivo ou exclusivo na expressão "envolvam autoridades influentes ou desvio de altos valores".
De todo jeito, teremos:
A∩B = 2/5 (2/3.3/5)
exclusivamente A = 1/5 (3/5-2/5) = A'
exclusivamente B = 4/15 (2/3-2/5) = B'
itens que não são parte nem de A nem de B = 2/15 [1-(2/5)-(1/5)-(4/15) = 1 - 13/15]
Caso interpretemos como exclusivo o ou, temos:
"envolvam autoridades influentes ou desvio de altos valores" = A' + B'= 7/15 que é menor que o resto, a parte não prioritária (8/15).
Caso interpretemos como inclusivo o ou em "envolvam autoridades influentes ou desvio de altos valores", temos:
"envolvam autoridades influentes ou desvio de altos valores" = 13/15
o resto = 2/15
a parte prioritária é superior (13/15) à parte não prioritária (2/15).
Logo, o gabarito depende da interpretação do ou.