-
Para cada equipe temos que escolher 3 analistas de cada especialidade, portanto teremos uma combinação:
C5,3 x C7,3 x C6,3 = 7000
-
Entendo um pouco diferente do colega Danilo Capistrano.
Penso que haverá a possibilidade de escolher um analista contabil + um analista educacional+ um analista processual (3 analista de especialidades distintas)
Logo,
5! + 7! + 6! = 5880.
Ou seja, o (+) significa que a equipe tem que ser formada por cada um dos analistas (obrigatório - adição).
-
7000.
c5,3 = 10
C7,3=35
C6,3=20
C5,3 X C7,3 X C6,3 = 7000
-
Pelas aulas que já peguei em cursinho os professores falam quando aparecer: equipe, senhas, códigos, anagramas e numero de telefone usar o ARRANJO!
-
Gente, Não procure chifre na cabeça de cavalo !
3 analistas, 7 analistas educacionais para 3 vagas, tenho o analista 1 2 3 4 5 6 7, se eu escolher o analista 1 2 3 ou escolher o 3 2 1, tem alguam diferença na ordem, ou equipe formada ? NÃO ! então mete combinação ! assim como para os demais.
C7,3 = 35
C5,3 = 10 35X10X20 = 7000
C6,3 = 20
-
A ordem dos fatores não importa e não pode haver repetição de elementos, então devemos usar combinação simples, através da seguinte fórmula:
C(m,p) = m!
m!(m-p)!
Combinação de 5 analistas contábeis com equipe com 3 componentes:
C(5,3) = 10
Combinação de 7 analistas educacionais com equipe com 3 componentes:
C(7,3) = 35
Combinação de 6 analistas processuais com equipe com 3 componentes:
C(6,3) = 20
Agora basta multiplicar os resultados:
10 x 35 x 20 = 7000
Questão correta!
-
Não estou entendendo mais nada.
Nesta questão, todo mundo disse que se tratava de arranjo:
Q392182 Prova: CESPE - 2014 - TC-DF - Técnico de Administração Pública
Disciplina: Raciocínio Lógico | Assuntos: Análise Combinatória;
Considerando que, em um planejamento de ações de auditoria, a direção de um órgão de controle tenha mapeado a existência de 30 programas de governo passíveis de análise, e sabendo que esse órgão dispõe de 15 servidores para a montagem das equipes de análise e que cada equipe deverá ser composta por um coordenador, um relator e um técnico, julgue os próximos itens.
A quantidade de maneiras distintas de serem escolhidos 3 dos referidos servidores para a montagem de uma equipe de análise é superior a 2.500.
E na presente, que é combinação.
Qual a diferença entre ambas????
-
André,
na questão que você postou, a solução é por arranjo pelo seguinte motivo: a questão especifica as funções que cada um dos três servidores escolhidos irão desempenhar. Assim, p.ex., se forem sorteados os servidores: Maria para a função 1, Carla para a função 2 e Pedro para a função. Isso é diferente de os mesmos servidores Maria, Carla e Pedro serem sorteados, porém mudando as funções, p.ex.: Maria para a 2, Carla para a 3 e Pedro para a 1. A ordem nesse caso é importante, pois vai proporcionar opções diferentes de configuração do grupo de sorteados.
Em contrapartida, na questão do MEC, a resolução é por combinação pelo seguinte motivo: ele diz, p.ex, que tem 5 analistas de contabilidade para ocupar 3 cargos, mas ele não específica os cargos, só diz que são 3 de analista de contabilidade: são iguais. Não temos o cargo dde analista para o setor x, o segundo cargo para o setor y e o terceiro para outro setor, p.ex. Portanto, se sortear os servidores Maria, Carla e Pedro eles ocuparão o cargo de analista, da mesma forma se a ordem do sorteio for diferente. A ordem, portanto, não nos dá opções de montagem da equipe diferentes.
-
Obrigado pela ajuda, Vanessa!
:)
-
Vamos considerar que cada equipe deve ter
exatamente três analistas de cada especialidade, precisamos escolher,
separadamente:
1) 3 analistas contábeis entre 5 existentes;
2) 3 analistas educacionais entre 7 existentes;
3) 3 analistas processuais entre 6 existentes.
Para cada um desses grupos,
a ordem de escolha dos analistas não interfere na contagem, logo, utilizaremos
Combinação Simples, então:
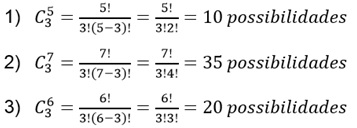
Logo, 10 x 35 x 20 = 7000 possibilidades.
Assim, a quantidade de
maneiras distintas de se formar equipes com exatamente três analistas de cada
especialidade em cada equipe é superior a 5.000.
RESPOSTA: CERTO
-
pq multiplicar os 3 valores e nao somar??
-
Princípio Fundamental da Contagem (PFC):
Princípio multiplicativo: associado ao conectivo "e".
Todas as vezes que os elementos do calculo forem ligados pelo conectivo "e" faremos uma multiplicação desses elementos.
Princípio aditivo: associado ao uso do conectivo "ou".
Todas as vezes que os elementos do calculo forem ligados pelo conectivo "ou" faremos uma adição desses elementos.
pq multiplicar os 3 valores e não somar??
A análise de requerimentos de certificação de entidades educacionais,
no âmbito do Ministério da Educação, será realizada por uma equipe
formada por, no mínimo, um analista contábil, um analista educacional e
um analista processual.
A equipe será formada por, no mínimo, 1 analista contábil E 1 analista educacional E 1 analista processual.
Analista contábil x analista educacional x analista processual
A equipe não será formada por, no mínimo, ou 1 analista contábil ou 1 analista educacional ou 1 analista processual.
Questão: A partir de cinco analistas contábeis, sete analistas educacionais e
seis analistas processuais, a quantidade de maneiras distintas de se
formar equipes com exatamente três analistas de cada especialidade em
cada equipe é superior a 5.000.
Ele quer formar equipes com 3 analistas de cada especialidade.
Analista Contábil:
n= 5 (número total de analistas contábeis)
p= 3 (número de analistas contábeis que formarão a equipe)
A ordem não importa, como já foi explicado pela Vanessa. Logo, usa-se a combinação.
C5,3= 10
Analista Educacional:
C7,3= 35
Analista Processual:
C6,3 = 20
Analista contábil (10 maneiras diferentes) x Analista Educacional (35 maneiras diferentes) x Analista Processual (20 maneiras diferentes)= 7000 maneiras diferentes de se formar a equipe.
-
Exemplo usando o princípio aditivo:
Eu tenho 3 carros, 2 motos e 3 bicicletas.
Quantas maneiras distintas eu posso sair de casa utilizando um desses meios de locomoção?
3+2+3= 8 maneiras distintas.
Eu posso sair de casa utilizando OU um dos 3 carros OU uma das 2 motos OU uma das 3 bicicletas.
Eu não posso sair de casa ao mesmo tempo utilizando Um dos 3 carros E uma das 2 motos E uma das 3 bicicletas.
Logo, a multiplicação, nesse caso não rola.
-
nossa, cuidado com as opiniões, tem cada um tentando "ensinar", filtro para não se prejudicar, fica a dica. Não é arranjo, é combinação!
-
IC BERSERKER está errado. tem que multiplicar, sim. veja que a questão fala que é para montar equipes com analistas contábeis E analistas educacionais E analistas processuais. ou seja, na mesma equipe tem 3 contábeis, de forma independente, 3 educacionais e de forma independente, 3 processuais. Logo,
C(5,3) * C(7,3) * C(6,3) = 7000
-
É necessário se fazer 3 combinações. (C5,3) = 10 , (C7,3)= 35 , (C6,3) =20
10 x 35 x 20 = 7000
Gabarito : Certo
-
A fórmula de Carlos há um equívoco, devemos usar combinação simples, através da seguinte fórmula:
C(m,p) = m!
p!(m-p)!
Exemplificando na primeira combinação.
C(5,3) = 5! / 3!x2!
C(5,3) = 5x4x3! / 3! x 2x1
C(5,3) = 20 / 2
C(5,3) = 10
-
Serão feitas 3 combinações:
C(5,3) = analistas contábeis = 10
C(7,3) = analistas educacionais = 35
C(6,3) = analistas processuais = 20
O resultado disso é 7000.
-
Como o 7,3 dar 35 alguem pode explicar ^?
-
Leonardo, alguns comentários abaixo mostram a resolução do problema, mas nesse caso específico:
C7,3 = 7! / (7! - 3!) x 3! = 7.6.5.4.3.2.1 / (4.3.2.1) x (3.2.1)
Não precisa nem fazer as contas. Vai cortando os números iguais na divisão e sobram os números 07 e 05. Multiplicando os dois, chega-se a 35.
-
O que não entendi nesta questão é quantas equipes serão formadas. No enunciado diz que será uma equipe e depois na afirmativa diz " a quantidade de maneiras distintas de se formar EQUIPES".
-
Ândrea Guerreiro, é justamente isso o que a questão quer saber. Quantas equipes diferentes poderão ser formadas no total, dado o número de analistas e a regra de que cada equipe terá três analistas de cada área. Pra isso você deve usar análise combinatória, mais especificamente a combinação.
-
Para cada equipe temos que escolher 3 analistas de cada especialidade, portanto teremos uma combinação:
C5,3 x C7,3 x C6,3 = 7000
o segredo da questão está no "E", pois indica que devemos MULTIPLICAR o resultado de cada uma das equações que foram feito em separado, cuidado pois quando é "OU" apenas se SOMA.
-
Falou em montar equipes, duplas, trios, etc, já pode saber que é COMBINAÇÃO
-
7.000, amém?
-
Paula Arnaud, é o tal do princípio da contagem.
-
Serão feitas 3 combinações:
C(5,3) = analistas contábeis = 10
C(7,3) = analistas educacionais = 35
C(6,3) = analistas processuais = 20
Ao final você as MULTePLICA
10.35.20= 7000.
-
no final das combinaçoes vai dá 20.10.35
c5.3 c7.3 c6.3
-
Primeira pergunta:
a ordem importa? se sim, arranjo, senão combinação!
neste caso é combinação.
Combinação de 5 analistas contábeis com equipe com 3 componentes:
C(5,3) = 10
Combinação de 7 analistas educacionais com equipe com 3 componentes:
C(7,3) = 35
Combinação de 6 analistas processuais com equipe com 3 componentes:
C(6,3) = 20
10 x 35 x 20 = 7000
7000>5000