-
Item ERRADO, temos combinação:
C5,1 (contabeis) x C7,1(Educacionais) x C6,1(processuais) = 5 * 6 * 7 = 210
-
c5,1 * c6,1 * c7,1 = 210
-
Acho que meu comentário pode ajudar. Assim que eu li o enunciado já fui direto na combinação. A questão não deixa clara a ideia de retirar cada um para formar um grupo. Fique em dúvida. A minha resposta deu 120. Vendo as respostas dos amigos, vi o meu erro.
Atenção é tudo.
-
Como posso diferenciar o uso do arranjo pela combinação ?
-
Arranjo: a ordem dos elementos importa (vogal)
Combinação: a ordem dos elementos não importa (consoante)
é bobo, mas já me fez acertar várias questões de prova! :P
-
Allan,
Pense no seguinte exemplo, as placas de transitos são formadas por 3 letras,a Placa formada pelas letras ABC, é diferente da placa BCA logo isso é um arranjo pois a ordem importa.
agora pense nesse exmplo, uma comissão formada pelas pessoas ABC, será a mesma formada comissão se formado por BCA, repare mudei a ordem, mas a comissão é a mesma ou seja a ordem não importa aqui ! quando a ORDEM criar um novo evento igual no exemplo acima é arranjo !
-
Arranjo = importa a ordem
Combinação -> por eliminação, nao importa a ordem (não tem r)
-
Combinação. 35 maneiras, pois a equipe formada por "A B C" não é diferente da equipe formada por "B A C".
-
É só fazer por combinação de cada uma das áreas (contábeis / educacionais / processuais) e multiplicar:
C5,1 x C7,1 x C6,1 = 5 x 6 x 7 = 210
-
Entendi muito diferente. O QC poderia comentar essa questão, só para esclarecer. (O gabarito foi errado mesmo)
Pensei que fosse o seguinte:
A questão afirma que cada equipe terá apenas 1 de cada especialidade e de forma distinta, ou seja, retirando aquele que já foi escolhido. Dessa forma, arrumei a questão da seguinte forma. O limitador era a parte contábil que só tem 5.
Contábil - Educacional - Processual
1º 5 x 7 x 6 = 210
2º 4 x 6 x 5 = 120
3º 3 x 5 x 4 = 60
4º 2 x 4 x 3 = 24
5º 1 x 3 x 2 = 6
TOTAL = 420 equipes
-
Raphael, sua analise estaria correta se a questão estivesse dizendo pelo menos um analista de cada equipe. Como a questão esta dizendo exatamente um, vale o o raciocínio que você fez no numero 1.
-
Gente, uma forma muito fácil de descobrir se é arranjo ou combinação é pensar se a ordem dos elementos faz ou não diferença.
E aí você pergunta:
HÁ diferença? Então Arranjo.
NÃO há diferença? Então combinaÇÃO!
Nunca mais errei, técnica do professor Jairo Teixeira do CERS.
-
Raphael, eu entendi igualmente a vc.
Achava que a questao limitava quando usa a expressao exatamente um analista de cada equipe.
eu entendi o comentario do victor simoes, mas nao consegui entender a questao.
...
aí insisti muito pra tentar entender e entendi.
uma dica, faça a analise com a arvore de possibilidades... coloque letras e numeros para os analistas, e vc vai ver que sáo hipóteses diferentes.
essa limitaçao de 5 que vc e eu fizemos supera o que foi pedido na questao.
bons estudos cara.
-
desculpe a pergunta tola, mas é arranjo ou combinação??
-
Faça a pergunta- pode repetir? não, a própria questão te fala, equipes distintas, ou seja, descarte a hipótese de P.F.C, depois pergunte, a ordem importa? não, então só pode ser combinação!! o porquê não importa? porque, para formar a equipe,( a, b, c, d, e), pode ser utilizado (a, b, c, e, d), " pense como pessoas", não será a mesma equipe? então a ordem não importa! preste atenção que ele fala que só pode ser formada equipes com um analista de cada especialidade, logo, C 5,1 X C 7,1 x C 6,1 = 210. questão errada!
-
A
questão nos pede: “...equipes distintas com exatamente um analista de cada
especialidade em cada equipe.” Logo, fazendo por combinação simples temos:
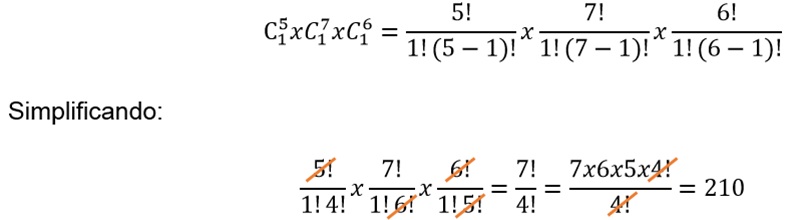
RESPOSTA: ERRADO
-
Arranjo Simples!
-
Basta utilizar o PFC : 5x7x6= 210
Gabarito errado!
-
Aqui poderia ser introduzido o conceito que:
C5,1 = C5,4
C7,1 = C7,6
C6,1 = C6,5
Sendo assim basta fazer uma simples multiplicação: 5x7x6 = 210
-
Não estou conseguindo entender de jeito nenhum por que a gente não divide 210 por 3!. A ordem não importa neste caso, de forma que a equipe Analista Processual + Analista Contábil + Analista Educacional é igual a equipe Analista Contábil + Analista Processual + Analista Educacional... e assim por diante.
Assim, na minha resolução, concordando com o Estevão, por ser uma combinação, o resultado é de 35 possíveis equipes.
5 x 6 x 7 (210), eliminando as permutações entre as posições do grupo (divide por 3!) = 210/6 = 35
Por favor, alguém sabe explicar por que o resultado é 210, não 35??
-
99,9% das questões que falam pra formar grupos ou comissões são de combinação.
Grupos\comissões = combinações.
Obs: Há vezes que não é aplicado tal conceito.
-
5 possibilidades de analistas contábeis x 7 possibilidades analistas educacionais x 6 possibilidades de seis analistas processuais
5 x 7 x 6 = 210
não tem segredo.
-
C(5,1).C(7,1).C(6,1)=210
GAB:ERRADO
-
5x6x7 = 210
-
Basta usar o Princípio Fundamental da Contagem
5x7x6 = 210
-
Item ERRADO, temos combinação:
C5,1 (contabeis) x C7,1(Educacionais) x C6,1(processuais) = 5 * 6 * 7 = 210
-
Minha contribuição.
Arranjo: problemas os quais a ordem de escolha importa.
Dica: placas, números, senhas etc.
Permutação: problemas os quais a ordem de escolha importa e a quantidade de elementos é igual a quantidade de posições, usa-se o fatorial.
Dica: anagramas, filas etc.
Combinação: problemas os quais a ordem de escolha não importa.
Dica: comissões, grupos, equipes, duplas etc.
Fonte: MPP
Abraço!!!