-
De acordo com o enunciado, na 1ª estação desembarcaram 2/3 dos passageiros que estavam no trem e ainda mais 10 passageiros, assim, montando a equação temos:
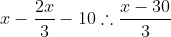
Na 2ª estação desembarcaram 2/3 dos passageiros que ainda estavam no trem e mais 10 pessoas, logo:

Exatamente assim aconteceu também nas 3ª , 4ª e 5ª estações.
3ª: 
4ª: 
5ª: 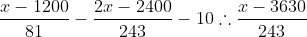
Da 5ª estação em diante, o trem trafegou com apenas 1 passageiro, então:
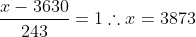
Somando todas as etapas e igualando a 3873:

Resposta: Alternativa B.
-
Parece demorado, mas são contas simples e rápidas.
Na 5ª Estação:
Após o desembarque Ficou 1 passageiro. Daí a pergunta é: quantos passageiros CHEGARAM na 5ª Estação (antes do Desembarque)? Resposta, Y
Y - (2/3Y + 10) = 1; então resolvendo a equação, 1/3Y = 11, então Y = 33 Y = quantidade de passageiros que FICARAM no trem após o desembarque na 4ª Estação (e seguiram para a 5ª Estação).
Na 4ª Estação: Quantos chegaram? (33 + 10) x 3 = 129 (= qtd de passageiros que ficaram no trem após o desembarque na 3ª Estação)
Na 3ª Estação: Quantos chegaram? (129 + 10) x 3 = 417
Na 2ª Estação: Quantos chegaram? (417+ 10) x 3 = 1281
Na 1ª Estação: Quantos chegaram? (1281+ 10) x 3 = 3873
Estação Inicial: 3873
A questão quer saber quantos passageiros desembarcaram nas 3 primeiras estações. Basta pegar o total de passageiros (3.873) e RETIRAR a qtd de passageiros que ficaram no trem após o desembarque na 3ª Estação.
FICA: 3.873 - 129 = 3.744
GABARITO: "B"
BONS ESTUDOS !!!!
-
nao consegui resolver ainda... deixa ver se entendi na primeira estacao sobrou x-30/3?
entao na segunda estacao eu nao teria q pegar esse numero x-30/3 e diminuir 2/3 -10?
-
Jo,
Se na primeira estação desembarcaram 2/3*X + 10, então sobraram 1/3*X - 10 no trem.
Se a cada estação você multiplicar os passageiros que estavam no trem por (1/3*X' - 10) e depois da 5a igualar o resultado destas multiplicações a 1, você encontra X. Mas da muito trabalho e a chance de errar é grande.
Essa solução do Silva F é muito boa, é bem melhor fazer do fim para o começo. A cada estação você sabe que restarão (1/3*X' - 10) passageiros no trem, ache quantos chegaram na 5a e vá voltando os cálculos.
Bons estudos, Elton
-
Uma dúvida, nós temos um "X" que entou na estação inicial ≠ primeira estação de desembarque.
PORQUE, pressupoem-se que as pessoas que saíram na estação 1 e o valor x são diferentes, já que não faria sentido entrar e sair na mesma estação, e mesmo porque na estação 1 é =====> x -(1/3x+10)
logo, teria um valor antes de 3873 da primeira estação, o X da estação inicial. Que seria de 11259.
Então seria assim:
1º estação desceu= 11259 -3873
2ºestação=3873 - 1281
---------------
Não é estranho isso???
-
Deus me defenderay =~~
-
Resolvo essa questão aqui nesse vídeo
https://youtu.be/i9-4MenezFA
Ou procure por "Professor em Casa - Felipe Cardoso" no YouTube =D