-
Resposta a)
C 5,3 x C 4,2 = 60
Combinação simples. Porém a banca considerou combinação com repetição, neste caso:
Cr 5,3 x Cr 4,2 = 350
-
Qual é a fórmula das duas combinações ( com e sem repetição ) ?
-
Edmir, as fórmulas são:
C n,p = n! / p!(n-p)!
Cr n,p = (n-1 + p)! / (n-1)!.p!
Bons estudos
-
ou seja..... a questão seria anulada pq a banca nao deixou escrito o que queria
-
Como pode dar uma resposta E? Se a banca considerou repetição não deveria ao menos ter mencionado isso?
-
Não precisa estar no comando da questão pelos cálculos já dar pra perceber a repetição. Por exemplo são 5 frutas: uva-pera-limão-caju-açaí. se tiver que escolher 3 dessas frutas você pode escolher uva-uva-uva- ou pera-pera-pera.....O comando da questão não restringiu por isso que as repetições entram nos cálculos.
-
Analisando a questão,
Utilizando
combinação simples:
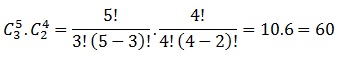
RESPOSTA: (A)
-
O gabarito certo é a letra A e não a letra E. Logo, a fórmula usada para se chegar a resposta foi a de combinaçao simples
-
Pois é Patrícia...o gabarito é letra A, não entendi porque vocês resolveram a questão por combinação com repetição (Cn+n-p, p) já que temos mais opções de escolha de frutas e hortaliças (n) do que a quantidades que queremos levar (p). Assim, afirmo que a questão deve ser revolvida por Combinação Simples.
-
1º Passo: é perceber que a questão é de combinação simples ( não há o que se falar em combinação com repetição)
2º Passo: temos 5 opções de frutas para escolher dentre essas 3 tipos. ex: poderia escolher: maçã,goiaba,banana a ordem não importa.
3° Passo: Temos 4 opções de Hortaliças para escolher dentre essas 2 tipos.
4° Passo: Montar o esquema, C5,3 x C4,2 ( 5,3 = 5 tipos de frutas para escolher 3) (4,2 = 4 tipos de Hortaliças para escolher 2)
5° Passo: Vamos a resolução....
C5,3= 5! 5! 5.4.3! 5.4 20
-------------- = -------------= --------- = (elimina-se os 3!) = --------= ------ = 10
3! ( 5-3) ! 3! 2! 3! 2! 2 2
C4,2= 4! 4! 4.3.2! 4.3 12
-------------- = --------= -------- = (elimina-se os 2!)= ---------= ------ = 6
2! (4-2)! 2! 2! 2! 2! 2 2
Agora vem aquela dúvida hein? temos o 10 e o 6 somar ou multiplicar? como o resultado é apenas parte do todo temos que multiplica-los
ou seja, 10x6 = 60. Gabarito letra A. Galera, os cálculos poderiam ser simplificados mas acredito que fazendo o passo a passo fica mais fácil para assimilar. Boa sorte povo!!
-
Comentário do professor para quem não tem acesso:
Analisando a questão,
Utilizando combinação simples:
C 5,3 x C 4,2 = 5! x 4! = 10x6 = 60
3! (5-3)! 4! (4-2)!
RESPOSTA: (A)
Faltou dizer porque a combinação é simples e não com repetição que parece ser a dúvida da maioria.
-
Dica: caso o conectivo usado seja E: " 3 tipos de frutas e 2 tipos de hortaliças " multiplicamos as possibilidades
já nas situações em que o conectivo for OU: " 3 tipos de frutas ou 2 tipos de hortaliças " devemos somar as possibilidades.
-
Ruim a explicação do professor, não explicou porque é combinação e não arranjo.
-
Pelo princípio da contagem (sem porcaria de fórmulas):
O que tenho:
5 tipo de frutas e 4 tipos de hortaliças
O que eu quero: (se a questão pede para que o cara escolha X os tipos, se pressupõe que não se pode repetir)
3 tipos de frutas e 2 tipos de hortaliças
Então:
Frutas: Escolho 3 dentre os 5 tipos = 5.4.3 e divido por 3.2.1 = 10
Hortaliças: escolho 2 dentre 4 tipos = 4.3 dividido por 2.1 = 6
OBS: A divisão é para eliminar as repetições com ordens diferentes. Exemplo: maça, banana e limão é igual a limão banana e maça! A ordem deles não importa.
A questão diz que ele pode escolher 3 tipos de frutas E hortaliças (multiplicação)
6.10=60 Gab: A
-
Não é arranjo pois a ordem não faz diferença.
-
Lazer Hawk, meu nobre eu não compreendi a lógica na sua maneira de resolver essa questão eu poderei dividir sempre pelo fatorial do meu subconjunto????? pois a meu ver não cabe aqui um P.F.C e sim combinação, eu gostaria de entender um pouco mais sobre essa maneira que vc usou ???
-
Eu já faria sem fórmula
5 tipos de frutas
2 tipos de hortaliças
3 tipo de frutas
2 tipos hortaliças
Pensando apenas na questão
5 tipos frutas vezes 3 tipos de fruta da segunda parte da questão é igual à 15
2 tipos de hortaliças mais 2 tipos da segunda parte da questão é igual à 4
4 vezes 15 = 60 FIM e Simples.
-
5 frutas e ele quer comprar 3 4 hortaliças e ele quer comprar 2 - Os números em negrito a quantidade
5/1*4/2*3/3=10 4/3*3/2=6 - Os que não estão e a probabilidade
10*6=60