-
(p ∧ q) ? (~p ∧ ~q)
(p ∧ q) -> (~p ∧ ~q) *** Não é tautologia***
-
tautologia ocorre quando a preposição é sempre verdadeira!
-
Fazendo a tabela verdade, o resultado é: V F F V ou seja, não é tautologia.
-
Prezados colegas, resolvi da seguinte maneira, porém gostaria do comentário de vocês para saber se realizei a questão de maneira correta:
Parti do princípio básico de matemática, primeiro resolvo o que está entre parênteses e depois os demais.
Sendo assim, o resultado da primeira preposição será:
primeira preposição
p e q - na conjunção as duas afirmativas têm que ser verdadeiras para ser válida. logo, é Verdade
segunda preposição
não p e não q - na conjunção as duas afirmativas têm que ser verdadeiras para ser válida a sentença, logo é Falsa
Agora temos: V DISJUNÇÃO F
Nesse caso, a disjunção só não será válida se o resultado for (FAFÁ DE BELÉM) F e F. Como encontramos V e F, a disjunção será verdadeira.
Sendo assim, é uma tautologia.
-
Questão tranquila.
''ERRADO''
-
É uma CONTINGÊNCIA.
-
Contingência ;)
-
SÉRIA, SO A INVERSÃO " ^ " PARA " V " SIMPLES.
-
Galera, macete para saber quando temos tautologia sem precisar de tabela verdade:
PROPOSIÇÃO v NEGAÇÃO DA PROPOSIÇÃO (disjunção)
PROPOSIÇÃO v NEGAÇÃO DA PROPOSIÇÃO (disjunção exclusiva)
PROPOSIÇÃO -> EQUIVALÊNCIA DA PROPOSIÇÃO (condicional)
PROPOSIÇÃO < - > EQUIVALÊNCIA DA PROPOSIÇÃO (bicondicional)
Nesses casos SEMPRE teremos tautologia.
-
Alguém pode me ajudar? Eu entendi o resultado da tabela VFFV, mas olhando essa proposição vi, pelo jeito, equivocadamente, que se tratava de um caso trivial de tautologia, por ex, quando temos "P v ~P" ou ainda "(P ^ Q) v ~(P ^ Q)". Neste último caso, não seria O caso da questão? Agora não entendi nada.
-
(P ^ Q) v (~P ^ ~Q)
(F ^ F) = F
(~F ^ ~F) = F
F v F = F
Não deu tautologia. (Essa maneira é mais rápida do que fazer tabela verdade).
-
Pessoal, quem tiver dúvida sobre a maneira de resolver essa questão, pode me pedir por e-mail.
NÃO CONSIGO COLOCAR A TABELA AQUI. :(
Email: renata20_mello@hotmail.com
P.S. A tabela que faço é simples e fácil de entender.
-
Na minha resolução deu
P ^ Q = (~p ∧ ~q) =
V V V F F F
F F F V V V
V F V F V V
F V V V F V
resultado:
(P ^ Q) v (~P ^ ~Q) =======
v f f
f v f
v v v
v v v
-
É UMA CONTINGÊNCIA!
RESULTADO DA TABELA
V
F
F
V
-
É sabido que uma proposição será uma tautologia quando a mesma não puder ser falsa, assim, montando uma tabela-verdade:
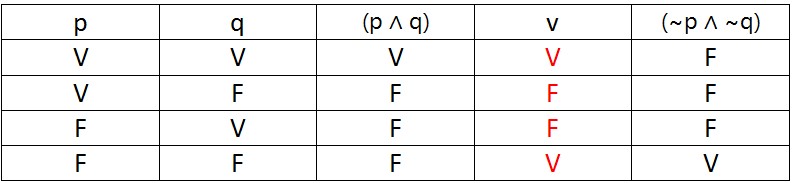
Resposta: Errado.
-
galera , vejo muitos comentários ae, e não sei se estão certo.. resolvi assim como o Eduardo Orem.. é uma tautologia, pois a disjunção não tem como ser falsa.
-
Uma dica: Parem de ficar procurando BIZU sobre RLM, pois isso só vai complicar vocês cada vez mais. RLM é uma matéria tranquila quando se aprende de maneira simples e correta.
Indico o Prof.Josimar Padilha, é excelente !!
Força guerreiros!!
-
Primeiro você deve negar se de certo nao é tautologia, se não der, então é
-
P Q ¬P ¬Q P^Q ¬P^¬Q (P^Q) V(¬P^¬Q)
V_____V _____F_____F______V________F____________V
V_____F______F_____V______F________F____________F
F_____V______V_____F______F________F____________F
F_____F______V_____V______F________V____________V
O NEGOCIO CHATO PARA FAZER TABELA AQUI É UMA BICODICIONAL RSRS ou uma contigência ^^
-
é uma contigência.
-
Gente quando penso que guardei a tabela verdade eu vejo questoes assim e me ferro, eu aprendir que na tabela da conjunção (^) só é verdade quando tudo for verdade eu estou vendo comentários aqui colocando verdade quando um dos conectivos for falso ou verdadeiro, isso procede? errei a questao porque fiz como aprendi de acordo com a tabela verdade da conjunçao, Por favor algum professor grave explicaçao
P Q P ^ Q v ~P ^ ~Q
V V V V F F
V F F V F V
F V F V V F
F F F V V V
Agora minha dúvida na tabela da disjunção inclusiva (v) "OU" somente será falsa quando da tudo falso, se eu estou comparando a tabela do P^Q usando conectivo OU
entre ~P ^ ~ Q EU TENHO QUE CONSIDERAR A TABELA do (v) "OU" , então alguém me explica porque não deu o resultado acima? NESTE RESULTADO é Considerado uma tautologia
-
Resultado: VFFV
-
É só olhar e vê se são equivalentes,caso não sejam nunca será tautologia.
Pau no Burro.