-
Se fizerem o desenho do diagrama fica mais fácil de visualizar e se organizar (por aqui não dá ).
"A" a intersecção com "B" = 6. (Homens altos e barbados que não são carecas são seis.)
Somente "A" = 5. (Sabe-se que existem 5 homens que são altos e não são barbados nem carecas.)
"A" a intersecção com "C" = ZERO. (Todos homens altos que são carecas, são também barbados.)
"A" a intersecção com "B" e com "C" = "X" (a ser encontrado) .
18 = 6 + 5 + X, então "X"=7
A questão pede "B" intersecção com "C", vamos chamar de "Y".
Outros dados:
Somente "B" = 5. (Sabe-se que existem 5 homens que são barbados e não são altos nem carecas.)
Somente "C" = 5. (Sabe-se que existem 5 homens que são carecas e não são altos e nem barbados.)
Façam o diagrama e visualizarão a seguinte equação:
5 + 5 + 5 + 6 + 7 + Y = 32
Y =4.
GABARITO: "A"
-
Gostei muito do comentário de Silva F!
Só acrescentando: Consegui encontrar o valor de y da seguinte forma:
22 = 5+6+7+y
22 = 18+y
y = 4
-
não entendi a informação: Todos homens altos que são carecas, são também barbados. Pela explicação de Silva F, isso significa 0 para A interseção com C.... mas não "entrou na minha cabeça", alguém pode me ajudar?
-
JACKELINE LEMES
"A" a intersecção com "C" = ZERO Pois não existe APENAS homens altos e carecas ( a intersecção c). Os homens altos e carecas são também barbados ("A" a intersecção com "B" e com "C" )
-
Estou com a Jaqueline Lemos. Tb não consegui entender pq é zero a intersecção de A e C. Para mim, o zero vai na intersecção dos 3 (A B e C) pela frase (Todos homens altos que são carecas, são também barbados.)
-
Resposta: (a)
18 Homens altos
22 Homens barbados
16 Homens carecas
Excluindo os homens altos, ficamos com:
22 - 5 = 17
16 - 5 = 11
17 + 11 = 28
32 Homens totais - 28 Homens barbados e carecas = 4
-
Daniela Matos, na intersecção ABC é igual a 7. na intersecção AC não tem valor nenhum.
18A + 22B+16C=32
HAB=6 , HABC=x, HA=5, HB=5, HC=5, HBC=? (Este é o que procuramos)
ai soma (HA+HB+HAB+HC)=21
No conjunto AB já tem 11 e tem que fechar 18 homens altos então intersecção ABC é 7.
SOMA 7+21-32= 4
-
O comentário da Silva F foi bastante esclarecedor. No caso de dúvidas resolva colocando em conjuntos... Com o tempo e treino resolveremos de forma mais direta e prática como os demais colegas. Bons estudos!
-
Questão divertida! .
-
Essa é uma daquelas clássicas! Eu por exemplo só consegui resolvê-la por diagrama. Sem isso, pra mim, se torna quase impossível.
-
Resolvendo pelo diagrama de Venn:
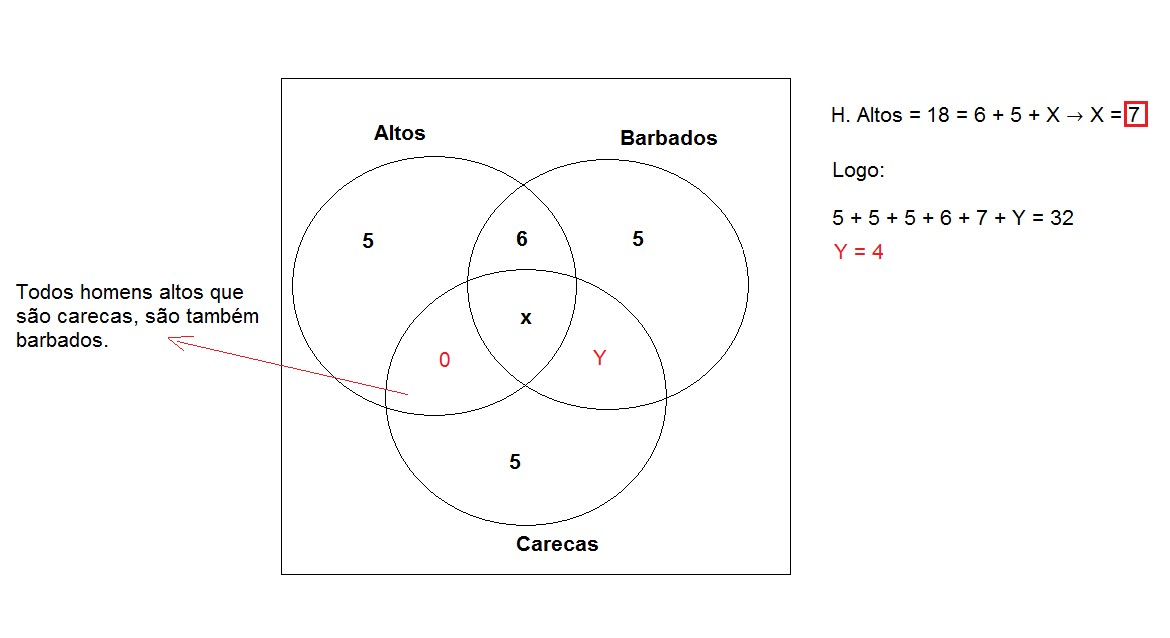
Resposta: Alternativa A.
-
Por que a intersecção A e C é 0 ?
-
Mateus,
A questão disse que todos os homens que são (A)ltos e são (C)arecas, são também (B)arbados.
Logo, nenhum homem é só Alto e Careca, por isso AeC=0
-
Peraí... A questão quer Teoria dos Conjuntos ou Proposição. Demorei meia-hora e errei.
-
TOTAL DE HOMENS = 32
SÃO ALTOS (A) = 18
SÃO BARBADOS (B) = 22
SÃO CARECAS (C) = 16
SOMENTE ALTOS = 5
SOMENTE BARBADOS = 5
SOMENTE CARECAS = 5
ABC (INTERSECÇÃO) = 7
AB = 6
AC = 0
BA = 6
BC = 4
5 + 5 + 5 + 7 + 6 + 0 + 6 + 4 = 32
GABARITO A
-
Só chutando!!!!!!!!!!!!!!!!!!!!!!!!!! errei feio e nem sabia o que eu tava fazendo. kkkkkkkkkkkkkkkkkkkkkkk
-
Pessoalmente, acho que nessas questões um pouco mais complexas, vale a pena desenhar o diagrama. O mais difícil aí é organizar as ideias, e nisso o diagrama ajuda bastante
-
Alguém poderia me explicar pq o resultado final é 13? Encontrei o valor BC:4.
-
Se a resposta é 4 o gabarito deve ser D, e não A como o site informa.
-
Estava igual um maluco fazendo e refazendo a questão porque o gabarito dá 13 e quando venho ler os comentários descubro que todos acharam 4 como eu. Esse gabarito deve estar errado. Não tem como ser 13.
-
Gabarito está errado. O correto é 4, letra D e não A.
-
silva F só não entendi pq vc pegou o 18 dos "altos" para achar o valor de X7, pode me ajudar?
-
Que bruxaria é essa: o resultado da maioria dando 4 [alternativa D], mas as estatísticas da questão marcam a A [13] como a mais respondida [e como resposta correta]?
É o IBOPE participando do Qconcursos?
-
fiz tres vezes esta questao e deu 13 como resposta, por favor alguém poderia me explicar com mais clareza como fazer esta questão? Agradeço muitissimo
-
Alto Com Barba Careca = 7
Alto Sem Barba Careca = 0
Alto Com Barba Cabelo = 6
Alto Sem Barba Cabelo = 5
Baixo Com Barba Careca = 4
Baixo Sem Barba Cabelo = 5
Baixo Com Barba Careca = 5
Baixo Sem Barba Cabelo = 0
Obs: Um homem só pode ser alto ou baixo (32), careca ou com cabelo (32), Com barba ou sem (32)
Alto = 18 Baixo = 14 (32)
Barba = 22 Sem barba = 10 (32)
Cabelo = 16 Careca = 16 (32)
-
5+5+5+6+7= 28-32 =4
-
Pessoal, não entendi o porquê da intersecção ser igual a 4. `Por favor , alguém poderia me esclarecer? obrigada,
-
Por que não há vídeo explicativo do professor???
Acredito que há pessoas (como eu) que têm mais dificuldade em RLM e precisam de vídeo explicativo!
-
Fiquei careca e barbado e não consegui responder! Um video é melhor!
-
passei 30m enrolado na questão até entender que: Todos homens altos que são carecas, são também barbados ou AC => 0
depois disso só somar 5+7+6+x=22 x=4
-
Não entendi essa questão, pois de onde se tira o valor de intesecção 7????
-
Gab Letra A.
Vídeo com a resolução corre lá!
https://youtu.be/1qi_Hs8nLTI
-
Todo alto que é careca é barbado. Logo, a parte dos altos que são carecas mas não são barbados não existe, pois todos os altos carecas são barbados. É daí w tu tira a interseção
-
Realmente Gilberto Wrignt o vídeo é muito bom! Mil vezes melhor que a explicação do professor aqui nessa questão!
-
Para resolver a questão, deve-se entender esta parte:
Todos homens altos que são carecas, são também barbados.
Logo, não PODE HAVER APENAS HOMENS ALTOS E CARECAS, POIS TODOS OS HOMENS QUE SÃO ALTOS E CARECAS TAMBÉM SÃO BARBADOS. Ao se realizar o diagrama deve-se colocar 0 na interseção entre altos e carecas. Depois, basta ir preenchendo o restante das interseções.
-
A 'grande' sacada dessa é que a interseção APENAS altos e careca é ZERO. Daí o restante fica de boa de se fazer.
-
GABARITO LETRA A
É só eu que não entende os comentários do prof. de matemática aqui do Qconcurso?
Ficou massa o seu vídeo Gilberto Wrignt, o Qconcurso bem que poderia lhe contratar para resolver
as questões em vídeos de RLM, já que estamos abandonados nesta disciplina.
-
Acertei a questão, mas fico pensando o que tem na cabeça das bancas em colocar uma questão dessas? O candidato resolve meio mundo de questão e, a depender da prova, ainda tem a discursiva... Isso é querer maltratar mesmo viu. Se fosse no cespe, provavelmente eu usaria 3 opções: Deixaria em branco, chutava ou tentaria responder, caso ainda tivesse tempo, mas deixaria por último.
-
muito boa a questão.
-
Qual a necessidade disso na prática? vai tomar banho FCC!
-
É o tipo de questão que precisaria de vídeo explicativo, e o professor fez somente aquela demonstraçãozinha.. tsc tsc
-
Excelente vídeo de explicação do Gilberto Wrignt!!! Parabéns pela iniciativa. Uma simples atitude que até hj o QC não entendeu que as explicações de raciocínio lógico e matemático são mais eficazes através de vídeos!!!!
-
Não é difícil não...o detalhe que faz matar a questão está em: Todos homens altos que são carecas, são também barbados.
-
o dia todo estudando e vem uma questão dessas, dor de cabeça.
-
A = alto , B = barbado , C = careca
32 homens 18 A ,22 B, 16 C
A-B=6 18 - 6 = 12 A , 22 - 6 = 16 B
A = 5 12 - 5 = 7 A
Todos os homens altos e carecas, são barbados.
A-B-C= 7
B = 5 16 - 5 = 11 B 11-7 = 4 B
C = 5 16-5 = 11 C 11-7 = 4 C
Barbado e careca
B-C = 4
-
Vamos imaginar os conjuntos dos homens altos, barbados e carecas. Temos algo assim:
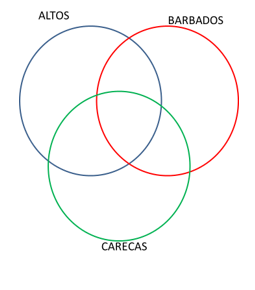
- Homens altos e barbados que não são carecas são seis.

- todos homens altos que são carecas, são também barbados. Ou seja, não há homens altos e carecas mas que não são barbados:

- Sabe-se que existem 5 homens que são altos e não são barbados nem carecas.
- Sabe-se que existem 5 homens que são barbados e não são altos nem carecas.
- Sabe-se que existem 5 homens que são carecas e não são altos e nem barbados.
Ou seja, temos o seguinte:

- 18 são altos, 22 são barbados e 16 são carecas. Logo, o número de homens altos faltando na figura é: 18 – 5 – 6 – 0 = 7. Podemos representá-los na parte central do gráfico, que ainda não foi preenchida:

Como temos 22 homens barbados, podemos dizer que a região vazia (homens barbados e carecas ao mesmo tempo, mas que não são altos) é formada por 22 – 6 – 7 – 5 = 4 elementos. Ficamos com o diagrama final:

Note que, de fato, temos 7 + 4 + 5 + 0 = 16 carecas, como havia dito o enunciado. Como vemos no diagrama, o número de barbados que não são altos, mas são carecas é igual a 4.
Resposta: A
-
Com todo respeito, extremamente fácil essa questão! Sabem como fiz? chutei kkkkkkkkkkkkkk
-
Prezados, um comentário que pode ajudar:
"Para resolver a questão, deve-se entender esta parte:
Todos homens altos que são carecas, são também barbados.
Logo, não PODE HAVER APENAS HOMENS ALTOS E CARECAS, POIS TODOS OS HOMENS QUE SÃO ALTOS E CARECAS TAMBÉM SÃO BARBADOS. Ao se realizar o diagrama deve-se colocar 0 na interseção entre altos e carecas. Depois, basta ir preenchendo o restante das interseções."
Ou seja, como não pode existir, no problema, altos e carecas, essa interseção será contada como 0 ou de forma única: A ∩ B = A ∩ B ∩ C
Bons estudos.
-
Gabarito:A
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
-
Gabarito:A
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
-
Pessoal, achei a resolução do exercício em vídeo. Bem simples, gostei!!!
https://youtu.be/cFc1IMnfO8c?t=3219
-
O número é= altos e Barbados que não são caras + Caracas - Altos
O número é= 6+16-18
O número é= 22-18
O número é= 4
Espero ter ajudado, com esse pensamento sobre a questão. "Vá e vença"
-
A resolução em desenho:
https://www.autodraw.com/share/L8MX54ICAQFF