-
1/4+1/4+1/4+1/4= total
amigo pagou apenas:
1/2 de 1/4=logo 1/8
restou 7/8 pra dividir por 3
logo 7/8*1/3
cada um pagara 7/24 a mais do combinado.
"devagar a gente chega lá"
Albertino de jesus.
-
O que não pode pagar a sua parte corretamente pagou 1/4 ÷ 2 ou 1/8.
Assim restou para os outros pagarem, 7/8, assim coube a cada um 1/3 do valor, ou seja,
7/8 . 1/3 = 7/24
Assim, 7/24 + 7/24 + 7/24 + 1/8 = 1 inteiro.
-
quem quiser resolver com valores...
Se o valor for 120> cada uma pagaria 1/4> 30 para cada, mas um só pôde pagar metade deste valor, ou seja, 15, sobrando mais 15 para os outros três. (15/3=5). Ficando a distribuição desta forma: 35+35+35+15=120
35/120 reduzindo> 7/24
-
Gente ... fiquei com a seguinte dúvida:
Cada amigo não teria que pagar o seu 1/4 + 7/24 ( 7/8 dividido pelos 3)?
-
1 inteiro dividido por 4 = 1/4
1/4 dividido por 2 → 1/4 * 1/2 = 1/8
sobra 1/8 dividido pros 3 amigos → 1/8* 1/3 = 1/24
1/4 + 1/24 = 6/24 + 1/24 = 7/24
-
ME COMPLIQUEI
-
pagou 1/2 de 1/4
então pagou 1/8
porem falta 7/8
então divide 7/8 pra 3 (amigos) = 7/24
-
Suponha que o valor total da conta é C. Cada amigo deveria pagar um quarto disso, ou seja, C/4. Um dos amigos só conseguiu pagar metade disto, ou seja, pagou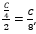 
, sobrando C/8 para ser dividido entre os outros três. Portanto, cada um dos outros três pagou a sua parte (C/4) e mais um terço do que sobrou do amigo que pagou menos (C/8). O valor pago por cada um deles foi de:
Portanto, cada amigo pagou 7/24 da conta original.
Resposta: B