-
Resposta correta: item (d)
Essa é uma questão que deve ser resolvida por meio da Combinação com Repetição. Para isso, usaremos o diagrama de bolinhas:
Temos 4 cores diferentes (vermelha, azul, amarela e branca). Sabemos que o total de orquídeas a serem escolhidas pelo cliente é igual a 6. Portanto, desenharemos seis pontos para representar esse valor 6:
. . . . . .
Agora, divideremos com uma barra esses 6 pontos em 4 partes que corresponderão às 4 cores disponíveis:
. . / . / . . / .
(parte 1) (parte 2) (parte 3) (parte 4)
O desenho está pronto! Agora é só efetuarmos os cálculos por meio de permutação com repetição. O total de símbolos dispostos acima é igual a 9 (os pontos se repetem 6 vezes e as barras se repetem 3 vezes):
9! = 9 x 8 x 7 = 84 (Resposta da questão)
6! 3! 3 x 2 x 1
-
veja bem são 04 cores diferentes logo há uma permuta de quatro , porém na compra de 04 orquideas ganha 02 que podem ser da mesma cor ou não ,neste caso temos também uma combinaçao de C6 2 . FICA ASSIM 4! = 4X3X2X1=24 + c6 2=15 x 4( são quatro cores que podem ser repetidas duas vezes cada uma) total = 24+60=84.
-
Este é um caso típico de combinação com repetição.
Em uma combinação com repetição todos os elementos podem aparecer repetidos em cada grupo até p posições.
A formula para combinação com repetições é uma combinação do tipo C (m+p-1, p)
Nesse caso m = 4 e p = 6
C(4+6-1,6) = C (9,6) = 9! / [6!*(9-6)!] = 84
Bons estudos! :)
-
Como os colegas já mencionaram, é um típico caso de combinação com repetição.
A fórmula para esse tipo de procedimento é C ( m + p - 1, p)
Admitindo-se que m seja a quantidade de cores das orquídeas e que p seja o número que o cliente pode escolher. Temos:
C ( 4 + 6 - 1, 6 ) = C (9,6)
Pronto, agora temos uma combinação simples, o que torna bem fácil a resolução.
C9,6 = 9! / 6! ( 9 - 6) ! = 9 x 8 x 7 x 6! / 6! 3! = 504 / 6 = 84
Logo, existem 84 maneiras diferentes de um cliente aproveitar a promoção.
Bons estudos.
-
Pessoal, eu fiz de uma forma diferente da de todos, porém não tenho certeza se meu raciocínio está totalmente correto, então se tem algum professor aí, gostaria que fizesse um check-up no meu raciocínio.
temos 6 orquideas e 4 cores para escolher
Cores
Ver
Azul
Amarela
Violetas Branca ______ _______ _______ _______ _______
Como mostra o diagrama uma cor obrigatoriamente já estará ocupando um dos espaços 3 cores + 5 espaços + 1 espaço fixo = 9
considerando que teremos 6 escolhas em um espaço de 9 opções, podemos considerar 9 espaços distribuidos em 6 opções.
logo teremos 9! (nove lacunas) dividida por 6! (opções) de e 3 cores que poderão se repetir
Violetas/ cores 9 8 _ _ 7 _ X X X X X X (simplificação) restam 3 espaços resultantes da subtração do número total de lacunas (espaço) - (menos) o número de produtos (opções/integrantes) diferindo assim um fatorial de 3 (3!)
como podem ver a partir desse raciocínio formei a fórmula 9! / 6!(9-6)! ou n! / p! (n-p)!
logo: 9*8*7*6! / 6!*3! => 9*8*7/ 3! (simplificação) => 504/6 = 84 LETRA D
-
Continuo sem entender.... alguém poderia explicar melhor essa questão????????
-
irmão , não sou muito bom não mais vou tentar te esplicar ai:
quando a combinação e com repetição a formula e e mesa da combinação normal , só que envez do texto de dar o numero que vai ser usado , voçê tem que achalo este exemplo ai temos 4 cores porem 6 orquideas então fica 4 das cores 6 das orquedeas -1 (não me pergunte daonde vem este -1 , so sei que a formula e assim) que vai dar C 9 , 6
-
Para resolver esta questão, vamos aplicar uma "manha" bem barbadinha.Vamos representar as 6 orquídeas com palitinhos:
| | | | | |
Agora, como temos 4 cores diferentes de orquídeas, vamos fazer uma suposta disposição das 6 orquídeas de forma a comprar cores diferentes:
vermelha azul amarela branca | + | | + + | | | Note que nesta disposição, comprei 1 orquídea vermelha, 2 orquídeas azul, nenhum orquídea amarela, 3 orquídeas branca.
Veja que o que eu estou fazendo nada mais é do que intercalar 3 sinais de soma no meio dos 6 pauzinhos que representam as orquídeas, portanto, se pensarmos que temos na verdade 9 elementos para permutar (6 orquídeas mais 3 sinais de soma), podemos ver o número total de compras que podemos fazer.
| | | | | | + + + Estes são os elementos que queremos permutar, inclusive, esta disposição que está aí, é uma possível compra das orquídeas, em que eu irei comprar 6 orquídeas da cor vermelha.
Agora, para calcular o número de permutações destes elementos, devemos utilizar a fórmula da permutação de 9 elementos com repetição de 6 elementos e 3 elementos, que fica assim:
P9 / P6 . P3
9.8.7.6! / 6! . 3. 2. 1
Vamos simplificar os fatores em comum:
3.4.7=84
-
Combinação com repetição: ocorre quando a permutação e maior do que o número de escolha.
N=4 orquídeas de 4 cores P=6 Escolha do cliente.
C (n+p-1, p)
C (4+6-1,6)
C 9, 6 = 84
-
só pode ser um nº parrrrr
-
A ordem dos elementos não é importante. Então é um caso de combinação.
C6;4=6!/4!(6-4)!=6!/4!2!=6.5.4!/4!2.1=15
-
Pessoal,
O gabarito dessa questão me deu a letra A como certa? É isso mesmo?
-
A combinação com repetição ocorre quando a quantidade de opções no subgrupo "p" é maior do que no grupo (no conjunto universo "n").
A questão nos informou que o conjunto universo "n" é de orquídeas de cores vermelha, azul, amarela e branca, sendo então n=4.
Informou também que pelo fato da promoção, poderá escolher 6 orquídeas, sendo então p=6.
Outra fórmula para se escrever a Combinação com Repetição, além das que os colegas informaram abaixo, é a seguinte:
C Rep. n,p = (n + p - 1)! / (n - 1)! p!
Seguindo a fórmula, teremos: C Rep. 4,6 = (4 + 6 - 1)! / (4 - 1)! 6!
C Rep. 4,6 = 9! / 3! 6!
C Rep. 4,6 = 9x8x7x6! / 6! 3x2x1
C Rep. 4,6 = 9x8x7 / 3x2x1 => Simplificando 3 com 9 e o 2 com o 8, teremos C Rep. 4,6 = 3x4x7 / 1
C Rep. 4,6 = 84
-
De acordo com os dados do enunciado,
temos um caso em que o número de permutação (4) é maior que o número de
escolhas (6), quando isso acontece, usa-se a fórmula da combinação com repetição, assim:
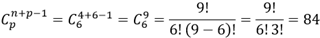
Letra D.
-
Muitos colegas não tem domínio da matéria. Então sejamos cuidadosos nos comentários. Somente a fim de ajudar os demais usuários, é importante ressaltar que o comentário da colega "doceisabel" não está correto!
Bons estudos!
-
https://www.youtube.com/watch?v=RZyAEQx_wS4
com essa aula fica muiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiito fácil, mas a moral dessa questão é que todas as alternativas são impares, exceto a letra "D"
-
Fiz o calculo analisando opção por opção. Demourou um pouco, mas quando percebi que tinha ultrapassado 45 opções ( alternativa C ) já marquei a unica alternativa possivel. Letra D
-
Galera esse caso COMBINAÇÃO COM REPETIÇÃO
P=pedaço (escolher 6 orquídeas)
N=total (vende orquídeas de 4 cores)
FORMULA
Cr=(n.p)=(N+P-1)
--------------------------
P!(N-1)!
Substitui os valores:
(N+P-1)! = 4+6-1= 9!
P!(N-1)! = 6!(4-1)= 6!(3!)
Resulado:
9!
6!3!
9! = 9x8x7x6 ! Para no 6 pra poder cortar com o de baixo
6! 3!= 3x2x1
Ficou = 9x8x7
3x2x1 = Simplifica tudo e resolve a conta = 84
-
Gab (E)
Cr= (N+P-1)!
P!(N-1)!
Onde N é o que vc tem no caso 4 orquideas diferentes, e P é o que vc quer no caso 6, agora é só jogar na fórmula e correr para o abraço.
-
Essa é atípica.
-
A+B+C+D= 6
C(9,6)= 9!/6!*3!= 9*8*7/6= 84
Letra D
-
Só acertei porque chutei no unico numero par que há.
-
Veja que temos n = 4 tipos de cores, e vamos pegar k = 6 elementos (orquídeas). Naturalmente, podemos repetir as cores das orquídeas. Estamos diante de um caso de combinação com repetição, cuja fórmula é:






Resposta: D
-
Combinação com repetição:
n = 4
K = 6
C = (4 + 5)!/ 6! . 3!
C = 84
-
Minha contribuição.
Veja que temos n = 4 tipos de cores, e vamos pegar k = 6 elementos (orquídeas). Naturalmente, podemos repetir as cores das orquídeas. Estamos diante de um caso de combinação com repetição, cuja fórmula é:
9! / 6!x3!
9 x 8 x 7 x 6! / 6! x 3!
9 x 8 x 7 / 3!
9 x 8 x 7 / 3 x 2 x 1 = 84
Abraço!!!
-
Questão simples. Talvez seja difícil pra quem ainda não deu uma olhada no assunto.