-
Alguém poderia me mostrar como chegar à resposta dessa questão? Obrigado!
-
"Se nevar então vai congelar" é uma proposição condicional que obedece à estrutura: "Se A então B" e sabendo-se que cada premissa (A e B) pode assumir apenas dois valores (V ou F), vamos analisar os resultados possíveis para essa condicional.
Na tabela verdade para A -> B (leia-se 'Se A então B'), temos
A B | A -> B
--------------
1) V V | V
2) V F | F
3) F V | V
4) F F | V
Instrução para usar a tabela-verdade: após assumir um valor (V ou F) para uma dada premissa (A ou B), procure na coluna da tabela-verdade o(s) valor(es) verdadeiro(s) correspondente(s), que indicará os valores possíveis para a outra premissa.
Então:
1º: se A então B, e afirmo que A ocorreu. Se eu afirmar A, poderei concluir que B ocorreu?
Sim. Pois a condicional implica que se ocorrer A então B também ocorre.
Usando a tabela-verdade: Para A verdadeiro (V), temos apenas um valor 'V' em A->B; logo A->B só será 'V' se B for 'V'.
Argumento válido, temos aqui uma tautologia.
2º: se A então B, e nego que A ocorreu. Se eu negar A, poderei então negar B também?
Não, porque a condicional não restringiu a ocorrência de B à ocorrência de A (B pode ocorrer sem que A ocorra).
Usando a tabela-verdade: Para A falso (F), temos DOIS valores 'V' em A->B; logo B poderá assumir os valores 'V' ou 'F'.
Essa conclusão é uma falácia.
3º: se A então B, e afirmo que B ocorreu. Se eu afirmar B, poderei então afirmar A?
Não. Pois, da mesma forma, B pode ocorrer sem que A ocorra.
Usando a tabela-verdade: Para B 'V', temos DOIS valores 'V' em A->B; logo A poderá assumir os valores 'V' ou 'F'.
Essa conclusão é uma falácia.
4º: se A então B, e nego que B ocorreu. Se eu negar B, poderei então concluir que A também não ocorreu?
Sim. Pois, segundo a condicional, não é possível não ocorrer B ocorrendo A, porque se A ocorrer, B também ocorrerá.
Usando a tabela-verdade: Para B falso (F), temos apenas um valor 'V' em A->B; logo A->B só será 'V' se A for 'F'.
Argumento válido, temos aqui uma tautologia.
Ficamos assim então:
I) Se nevar então vai congelar. Não está nevando. Logo, não vai congelar: 2º exemplo acima.
II) Se nevar então vai congelar. Não está congelando. Logo, não vai nevar: 4º exemplo acima.
Obs: o argumento (II) acima ficaria mais coerente se a redação observasse a ordem temporal das premissas, uma vez que "Se nevar" é o termo antecedente, e "vai congelar" é o consequente: "Se nevar então vai congelar. Não está congelando. Logo, não nevou".
-
Sabendo que na Tautologia a conclusão sempre será verdade e que na Falácia poderá ser verdade ou falso, e sabedores da tabela verdade, que na condicional só será F, se o antecedente for V e o consequente for F, analisemos os casos. Lembrando que quando se trata de análise de premissas, devemos considerá-las todas corretas e partirmos da mais simples, portanto:
Argumento I: ( F ) ( V ) ou ( F )
Se nevar então vai congelar. ( V )
Não está nevando. ( V )
Logo, não vai congelar.
Partindo do argumento mais simples – Não está nevando, e considerando verdade, então se nevar será Falso, mas a premissa é verdadeira e para tanto, o consequente poderá ser verdade ou Falso, adquirindo assim duas possibilidades, ex. de Falácia. Logo, não posso afirmar se vai ou não congelar.
Argumento II: : ( F ) ( F )
Se nevar então vai congelar. ( V )
Não está congelando. ( V )
Logo, não vai nevar.
Partindo do argumento mais simples – Não está congelando, e considerando verdade, então se congelar será Falso, mas a premissa é verdadeira e para tanto, o antecedente tem sempre que ser Falso, pois se for verdadeiro, a premissa será Falsa, ex. de Tautologia, Logo posso sempre afirmar que não vai nevar.
-
A questão poderia ser anulada. Conforme as explicações dos outros comentários as tabelas-verdade sempre demonstram uma contingência e não uma tautologia como afirma a questão.
Tautologia
Vamos usar como exemplo a mais simples tautologia de todas,
P ∨ (¬P) ,
cuja a tabela-verdade é a seguinte:
Conforme você pode observar acima, a última coluna da tabela-verdade da proposição P ∨ (¬P) contém, nos dois casos possíveis, somente valores V. Isso ocorre porque o conectivo "ou" é V quando pelo menos uma das proposições P e ¬P é V. Tal proposição é um exemplo de tautologia.
Contingência
A contingência ocorre quando há tanto valores V como F na última coluna da tabela-verdade de uma proposição. Exemplos: P∧Q , P∨Q , P→Q ...
fonte:http://logicadescomplicada.blogspot.com.br/2010/08/tautologia-contradicao-contingencia.html
-
Discordo que a questão deveria ser anulada. Fiz as tabelas verdades e realmente a primeira é falásia e a segunda é tautologia.
-
Depois de ler e muito pensar, ainda não entendi onde está o erro no meu raciocínio, vejam só:
N --> C = (v) ~N (v) F --> C = (v) Sendo assim, independente do valor de C (v/f) o arg. 1 será verdadeiro. TAUTOLOGIA
Porém é claro, se você não considerar o argumento 1 e simplesmente a CONDIÇÃO, não é uma tautologia, mas ele pede o correto e especifica o argumento, então acredito que deve ser levado em conta o contexto/situação.
N ---> C = (v) ~C (v) N --> V = v/f Sendo assim, dependendo do valor de N (v/f) o arg. 2 será verdadeiro/falso. FALÁCIA
Considerando a CONDIÇÃO seria Falácia de todo jeito.
RESPOSTA PRA MIM: LETRA D
GABARITO: LETRA C
(Designa-se por falácia um raciocínio errado com aparência de verdadeiro).
Bem, essa foi a forma que pensei, talvez não tenha interpretado bem a questão ou não entendi bem o que é uma falácia... Alguém pode mostrar onde eu errei ?
-
É sabido que um argumento é válido se,
e somente se, todas às vezes que suas premissas são verdadeiras, sua conclusão
também o é.
Assim, usaremos aqui o Método Direto, onde dado um argumento,
chamamos Método Direto a construção das tabelas-verdade das premissas e da
conclusão para avaliar se:
i)
Em
todos os casos (linhas da tabela-verdade) em que as premissas são verdadeiras a
conclusão é verdadeira e, portanto, o argumento é válido; ou
ii)
Há
um caso (linha da tabela-verdade) com premissas verdadeiras e conclusão falsa
e, portanto, o argumento não é válido.
Argumento I: Se nevar então vai congelar. Não está
nevando. Logo, não vai congelar.
Analisando o argumento abaixo, temos a
tabela-verdade a seguir:
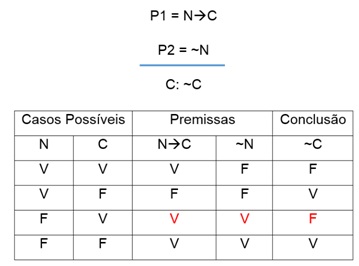
Logo,
temos aqui um argumento inválido ou uma falácia, ou seja, um argumento
logicamente inconsistente, sem fundamento, inválido ou falho na tentativa de
provar eficazmente o que alega.
Argumento II: Se nevar então vai
congelar. Não está congelando. Logo, não vai nevar.
Analisando o argumento abaixo, temos a
tabela-verdade a seguir:
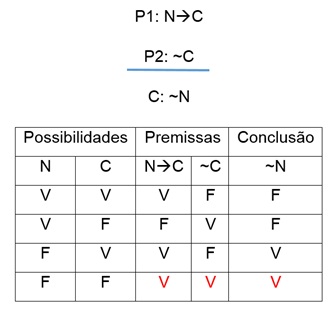
Logo, o argumento é válido, ou seja temos uma
tautologia.
RESPOSTA: (C)
-
Argumento 1
P1 . A => B P2 . ~A C . ~B
V F F
F F V
V V F
V V V
P1 . A => B P2 . ~B C . ~A
V F F F V F
V F V
V V V
No argumento 1, nas mesmas linhas onde as premissas são verdadeiras (as duas últimas) existe uma linha na qual a conclusão é falsa, a penúltima, tornando o argumento inválido. No argumento 2, na última linha, única em que as premissas são verdadeiras ao mesmo tempo, a conclusão também é verdadeira, fazendo com que o argumento seja válida. Logo, reposta certa letra C.
-
Perfeito, Elisangela Varonil. Tirou minha dúvida de forma clara e objetiva. Muito obrigado a vc e a todos que se dispõem em dar explicações.
-
Em raciocínio analítico, quando se tem a situação de 'Se A então B", a única solução que será uma tautologia é negando B.
Quer negar A ou afirmar B serão casos de falácias. Observem os exemplos:
Se eu bato em Tom, ele ficará machucado.
- Afirmando B: Tom foi machucado. Logo pode haver uma outra alternativa para a questão, como ele ser atropelado ao atravessar a ruam por exemplo.
- Negando A: Eu não bati em Tom. Mesmo assim ele pode ter apanhado de outra pessoa e ficar machucado da mesma forma.
Agora, quando eu nego B, ou seja, Tom não está machucado, eu com certeza não bati nele.
-
Essa questão parece ser cabulosa, mas com mt treinamento dá p/ fazer ela rápido.:
(caso não entendem o comentário, sugiro que procurem no youtube o professor Jhoni Zini do Focus Concurso ou Josimar Padilha do Gran concurso, foi com eles que aprendi fazer isso super rápido e fácil)
Segue o comentário do professor do estratégia
Argumento I:
P1 -> Se nevar então vai congelar.
P2-> Não está nevando.
Conclusão -> Logo, não vai congelar.
Vamos imaginar que a conclusão é F. Portanto, vai congelar. Agora vamos tentar tornar as premissas Verdadeiras (forçando o argumento a
ser inválido). Em P2 vemos que “não está nevando”. Assim, a primeira parte de P1(“nevar”) é F, de modo que P1 é V também. Foi possível ter a conclusão F quando ambas as premissas eram V. Ou seja, esse argumento é inválido (falácia).
Argumento II:
P1 -> Se nevar então vai congelar.
P2 -> Não está congelando.
Conclusão -> Logo, não vai nevar.
Assumindo que a conclusão é F, vemos que vai nevar. Agora vamos tentar forçar as premissas a serem verdadeiras. Para P2 ser verdadeira, é preciso que não esteja congelando. Porém com isso a condicional de P1 fica V->F, pois “nevar” é V e “vai congelar” é F. Ou seja, NÃO foi possível tornar as duas premissas V quando a conclusão era F. Isso mostra que este argumento é válido (ou uma tautologia).
GAB: C
-
Patrick Santana, essa foi a melhor explicação.
-
GABARITO: C
Argumento I:
P1 -> Se nevar então vai congelar.
P2 -> Não está nevando.
Conclusão -> Logo, não vai congelar.
Vamos imaginar que a conclusão é F.
Portanto, vai congelar. Agora vamos tentar tornar as premissas Verdadeiras (forçando o argumento a ser inválido).
Em P2 vemos que “não está nevando”. Assim, a primeira parte de P1(“nevar”) é F, de modo que P1 é V também.
Foi possível ter a conclusão F quando ambas as premissas eram V. Ou seja, esse argumento é inválido (falácia).
Argumento II:
P1 -> Se nevar então vai congelar.
P2 -> Não está congelando.
Conclusão -> Logo, não vai nevar.
Assumindo que a conclusão é F, vemos que vai nevar. Agora vamos tentar forçar as premissas a serem verdadeiras.
Para P2 ser verdadeira, é preciso que não esteja congelando. Porém com isso a condicional de P1 fica V-> F, pois “nevar” é V e “vai congelar” é F.
Ou seja, NÃO foi possível tornar as duas premissas V quando a conclusão era F. Isso mostra que este argumento é válido (ou uma tautologia).
Prof. Arthur Lima
-
Não teria um erro pelo fato de, na argumento II, a conclusão é "não vai nevar", no futuro? Porque se não está congelando, não tem como dizer se vai nevar ou não, só tem como afirmar que não está nevando. Isso não faz diferença?
-
Na boa, por essa explicação do Prof. Arthur Lima eu custei a entender.
Argumento I:
P1 -> Se nevar então vai congelar.
P2 -> Não está nevando.
Conclusão -> Logo, não vai congelar.
Para resolver coloca a conclusão como verdadeira, só isso. Agora vemos que não vai congelar é verdadeiro. Na P1 diz que vai congelar então é falsa. Na P2 diz que não está nevando e na P1 diz que está nevando. Aí a charada da questão P (V F) -->Q (F) = POR ISSO É UMA FALÁCIA.
Gab.C
-
Exato BRENO!
Pessima explicação do Prof. Arthur Lima, não da para entender nada
-
O argumento 2 é Tautologia:
(p -> q) <-> (~q -> ~p)
v v
f f
v v
v v
Repare que o "~q" está na frente do "~p" (~q -> ~p). O nome desta tautologia é contrapositiva.
-
Essa explicação do Professor Arthur é muito "meia boca". Complicado de entender, fiquei um tempão tentando resolver.
-
Foi assim que eu aprendi a resolver esse tipo de exercício, espero que ajude!
RESOLUÇÃO: Comece pelas premissas. Assume que a proposição simples é VERDADEIRA e depois resolva a proposição composta. Verifique agora o valor da conclusão. Se a conclusão for VERDADEIRA será uma TAUTOLOGIA e se for FALSA/INVIAVÉL será uma FALÁCIA.
ARGUMENTO I
Se nevar vai congelar. ---------------------------- p -> q = F -> FouV (não posso afirmar o valor de q, pois tanto V ou F a resposta seria V)
Não está nevando. --------------------------------- ~p = V
Conclusão: Logo, não vai congelar. ----------- ~q = V ou F (é inviavél, ou seja, uma falácia)
ARGUMENTO II
Se nevar vai congelar. ---------------------------- p -> q = F -> F = V (posso afirmar que p é F, pois se fosse V a resposta seria F)
Não está congelando. ---------------------------- ~q = V
Conclusão: Logo, não vai nevar. --------------- ~p = V (é uma tautologia)
-
MODO SIMPLES
COLOCA A CONLCUSÃO FALSA E AS PREMISSAS VERDADEIRAS.
SE FECHAR OU SEJA DAR CERTO, É PQ O ARGUMENTO É INVÁLIDO(F)
SE ERRO É O ARGUMENTO É VALIDO.
VEJA:
ARGUMENTO 1
NEVAR-------->CONGELAR V
Ñ ESTÁ NEVANDO V
LOGO, Ñ VAI CONGELAR F
NO SE ENTÃO É VERDADEIRO SE FOR V OU F NO COMEÇO, OU SEJA PODE OU NÃO NEVAR, NÃO TENHO COMO AFIRMAR SE NEVA OU NÃO.
-
Gab (C)
Argumento I
P1: N ---> C
P2: ¬N
C :¬C
*Note que essas premissas não da pra valorar atráves do Modus Ponens, assumindo que a premissa simples seja verdadeira ¬N(não vai nevar), não se tem o valor de C ou de ¬C. E também não da pra valorar usando o Modus Tollens, assumindo que a conclusão seja falsa ¬C(não vai congelar). Como o argumento é inválido por não poder se valorar, e utiliza frases reais, nós temos uma falácia.
Argumento II
P1: N ---> C
P2: ¬C
C : ¬N
*Aqui se vc utilizar o Modus Ponens, e afirmar que a premissa simples seja verdadeira ¬C(não vai congelar), vc consegue valorar o resto das premissas. E terás uma Tautologia, quando os valores de todas as premisas e a conclusão sejam verdadeiras.
-
Esperto não é quem acertou a questão, esperto é quem consegue aprender raciocínio lógico por letras, texto, kkkkkkkk, é preciso imagem...
-
O comentário da senhorita T.S. é o melhor para compreender. Caso alguém tenha dúvida, pode ver esse vídeo aqui!
https://www.youtube.com/watch?v=rNnQMV5cFU4
Vídeo do Professor Renato Oliveira fazendo exercícios idênticos!
Bons estudos!!
-
Ambos são falácias. O I) por razões já explicadas e o II) pq não se pode afirmar que não vai nevar, mas apenas que não está nevando; logo o II) é uma falácia, e a correta portanto é a letra a).
Força!
-
São proposições simples, não dá pra aplicar a tabela verdade ao meu ver.
Só congela se nevar, não está nevando, então não congela.
Se não está "nevando", não está congelando.
A banca erra no português para induzir os concorrentes ao erro.
-
Para conseguir entender tem que assistir essas aulas:
https://www.youtube.com/watch?v=3757ryqcEm8&list=PLul52lXn9jZ4M6sxzHZLveh40wh26RzKs&index=19
https://www.youtube.com/watch?v=i4cfrzMU4uw&list=PLul52lXn9jZ4M6sxzHZLveh40wh26RzKs&index=18
https://www.youtube.com/watch?v=bT_SxIOxwko&list=PLul52lXn9jZ4M6sxzHZLveh40wh26RzKs&index=29
Depois... ler a explicação do amigo CAVEIRA, FORÇA!
Resposta:
GABARITO: C
Argumento I:
P1 -> Se nevar então vai congelar.
P2 -> Não está nevando.
Conclusão -> Logo, não vai congelar.
Vamos imaginar que a conclusão é F.
Portanto, vai congelar. Agora vamos tentar tornar as premissas Verdadeiras (forçando o argumento a ser inválido).
Em P2 vemos que “não está nevando”. Assim, a primeira parte de P1(“nevar”) é F, de modo que P1 é V também.
Foi possível ter a conclusão F quando ambas as premissas eram V. Ou seja, esse argumento é inválido (falácia).
Argumento II:
P1 -> Se nevar então vai congelar.
P2 -> Não está congelando.
Conclusão -> Logo, não vai nevar.
Assumindo que a conclusão é F, vemos que vai nevar. Agora vamos tentar forçar as premissas a serem verdadeiras.
Para P2 ser verdadeira, é preciso que não esteja congelando. Porém com isso a condicional de P1 fica V-> F, pois “nevar” é V e “vai congelar” é F.
Ou seja, NÃO foi possível tornar as duas premissas V quando a conclusão era F. Isso mostra que este argumento é válido (ou uma tautologia).
Prof. Arthur Lima
-
Pra mim essa questão se encontra errada, pois ambas as assertivas são falácias, já que o examinador errou o tempo verbal do argumento II.
Quando negamos a 2º proposição de uma condicional, temos como garantir a negação da primeira também, ou seja, no exercício em destaque podemos garantir que não ESTARÁ nevando, e não que não IRÁ nevar, que são coisas distintas, já não temos como prever o futuro.
Pra corroborar com o gabarito a assertiva deveria ser: "Se for nevar então vai estar congelando. Não está congelando. Logo, não vai(irá) nevar."
-
Se, então Suficiente, Necessário
Congelar é necessário para nevar
Nevar é suficiente para congelar
Argumento I: Se nevar então vai congelar. Não está nevando. Logo, não vai congelar : FALSO, pois não nevar é suficiente para congelar
Argumento II: Se nevar então vai congelar. Não está congelando. Logo, não vai nevar. VERDADEIRO, pois congelar é necessário para que neve
GAB C
-
Para quem não entendeu, assista a resolução: www.youtube.com/watch?v=B0ZJcyMdY8A
Gab. C
Espero ter ajudado! Bons estudos.
-
Gente, me tirem uma dúvida por gentileza...
Para saber se um argumento é válido ou não, não se deve julgar a conclusão em v ou f é isso? Começo pela simples.
Mas por que em algumas premissas eu posso atribuir um valor na conclusão? Tipo essa aqui: Surfo ou estudo. Fumo ou não surfo. Velejo ou não estudo. Ora, não velejo. Confesso que estou confusa....rs
-
c-
_____________________________________________________________________________________________________________________
Argumento I: Se nevar então vai congelar. p->q.
Não está nevando: ~p = F
Logo, não vai congelar. ~q = F
em condicional, o argumento é inválido quando a premissa é verdadeira e a conclusão falsa:
v->v = V
f->v = V
f->f = V
v->f = F
Negar a premissa nao implica negação da conclusão. o argumento tb tem validade se a premissa for falsa.
_____________________________________________________________________________________________________________________
Argumento II: Se nevar então vai congelar. p->q
Não está congelando. ~q = F
Logo, não vai nevar. p = V
esse é caso de v->f = F. o que torna a afirmação inválida
-
A questão não é de toda ruim, mas a banca não sabe oq é TAUTOLOGIA, isso é fato, o argumento I é uma falácia (falso) mas o argumento II apesar de ser válido não é uma TAUTOLOGIA (onde todas as alternativas só podem resultar verdadeiras) mas sim uma contingência. Quiseram falar bonito e detonaram a questão.
-
I – Não vai congelar é a conclusão. “Se nevar, então vai congelar” e “não está nevando” são premissas verdadeiras. A premissa mais simples é não está nevando. Se não nevar é verdadeiro, nevar é falso. Na conjunção “se, então”, se a primeira ideia é falsa, a segunda pode ser verdadeira ou falsa. Então não é possível afirmar se vai congelar, pois a ideia pode ser verdadeira ou falsa. O argumento é inválido / falácia.
II – Se não congelar é verdadeiro, vai congelar é falso. F + F = V. Nevar é falso, então não nevar é verdadeiro. O argumento é uma tautologia.
O Argumento I é uma falácia e o Argumento II é uma tautologia.