-
Regras de Proposições Equivalentes:
se p então q, é equivalente a: ~p ou q, logo, eu devo:
1º: nego a primeira proposição (~p)
2º: trocar o sinal de se então por ou
3º: Manter o sinal da segunda proposição (q)
Ao fazer isso encontra-se a resposta. Lembrar que a negação do sinal de menor é maior ou igual e vice-versa.
-
|a| < 3 → b ≤ 4
P → Q
Equivale
~Q → ~P b > 4 → |a| ≥ 3
~P v Q |a| ≥ 3 v b ≤ 4
P ^ ~Q |a| < 3 ^ b > 4
e) b ≤ 4 ou |a| ≥ 3.
-
A equivalência de Se A então B é = se não B então não A
e tbm não A ou B.
Agora, vendo as questões a letra é se encaixa. Pois ele usou a equivalencia ~ A ou B. A negação de maior ou igual é "menor". Logo é a letra E.
-
Fiz assim:
A < 3 → B ≤ 4, vou negar essa proposição
A < 3 e B > 4, negando novamente para achar a equivalência
A ≥ 3 ou B ≤ 4
Letra E
-
Eu só consegui entender quando resolvi uma a uma as questões.
Comparando as tabelas.
Tabela do enunciado é A ->B
v v v
v f f
f v v
f f v
A única tabela que fica igual é a letra E: B v ~A
v f v
f f f
v v v
v v v
Em todas as outras alternativas as tabelas não batem com o enunciado.
Só consegui resolver depois de fazer todas as opções da questão.
Ainda sou gafanhoto nessa matéria e não decorei todas as regras de equivalência, negação..., então fiz o passo a passo (que não coube aqui).
Se eu estiver enganada, me avisem por favor?
Bons estudos a todos!
-
Existem certas Equivalências Importantes. Uma delas é:
(P → Q) é equivalente(˜P v Q) (É uma tautologia também (P → Q) ↔ ( ˜P v Q))
A negação de P: a >= 3
A expressão fica: a>= 3 ou b<= 4
Como é o conectivo OU(v), a ordem pode ser alterada:
E a expressão fica: b <= 4 ou a >= 3 - LETRA E
-
Não faço ideia como Sandro chegou naquela resolução, visto que, a negação da condicional não se faz da forma que ele fez. Acredito que a resolução se chega realizando a tabela verdade mesmo, como fez um colega acima.
Negação da Condicional se faz:
se p então q
p ^ ~ q
Ex: se faz sol, então vou a praia.
p = faz sol
q = vou a praia
a negação fica p ^~ q = faz sol E eu NÃO vou à praia.
-
Primeiro faz a equivalência com a técnica do inverte e nega e depois equivalência do se então com o OU.
abs
-
|a| < 3, então b ≤ 4
Dica: Para negar esses sinais, procede-se assim: a negação de < é ≥ e a negação de ≤ é > "e visse vessa"
Vamos resolver!
Considere |a| = p e b = q
Pela propriedade tem-se:
p -> q = ~q -> ~P
ou seja:
|a| < 3, então b ≤ 4 é igual a b > 4, então |a| ≥ 3
Em posse da nova situação (b > 4, então |a| ≥ 3), e como essa ainda não é uma das respostas da questão, vamos transformar na outra propriedade que diz:
p -> q = ~p ou q
Ou seja:
b > 4, então |a| ≥ 3 é igual a b ≤ 4 ou |a| ≥ 3
Alternativa correta: Letra E
-
Para mim a letra c também esta correta, pois:
P --> Q pode ser: P ^ ~Q / ~P V Q / ~p --> ~ q.
Assim, poderia ser: a<3 --> b<=4, a<3 ^ b>4
-
Olá,
Anderson, a letra C não pode estar correta, pois a transcrição da proposição b > 4 e IaI < 3 seria ---> ~ q ^ p , logo a tabela verdade não é a mesma de p ---> q.
tabela verdade para p ---> q tabela verdade para ~ q ^ p
V F
F V
V F
V F
-
Muito obrigada Jose Ailton ajudou mesmo!
-
Questão bem simples!
Vamos lá amigos:
Se |a| < 3, então b ≤ 4 ,
p = |a| < 3 ~p = |a| >=3
q =b ≤ 4 ~q = b > 4
Se p, então q
p ---> q
Vamos buscar a equivalente fazendo uma tabela verdade única, observando todas as assertivas
p q ~p ~q p --->q q ^ p (assertiva a) ~q v p ( assertiva b) ~q ^ p ( assertiva c) q v p (ass.d) q v ~p (ass. e)
V V F F V V V F V V
V F F V F F V V V F
F V V F V F F F V V
F F V V V F V F F V
Portanto letra e)
-
Sabemos que uma das equivalências da
condicional p → q
é ~p v q. Aqui podemos igualar p = |a| < 3 e q = b ≤ 4, assim, a negação de
~p = módulo de “a” é maior ou igual
a 3, então:
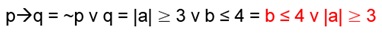
Obs.: p v q é equivalente a q v p,
para verificar, basta testarmos com a tabela-verdade de ambas.
RESPOSTA: (E)
-
Duas proposições são equivalentes quando possuem a mesma tabela verdade, ou seja, lendo o enunciado fica claro que ele busca a equivalência da expressão: se p então q. Há duas possibilidades de equivalência para essa expressão: (~q então ~p ), ou, (~p ou q ), observem as respostas e verão que as únicas possibilidades serão as alternativas b,d e e ( que utlizam o conectivo ou) aplicando a propriedade (~p ou q) chegaremos a alternativa "e", lembrando que vc pode alterar a ordem dos conectivos "ou" e "e"; (p ou q) é o mesmo que (q ou p)
-
Solução: basicamente quer saber o
que é equivalente a “|a| < 3 ->
b ≤ 4”
A equivalência do ‘->’ pode ser:
# Inverte
negando (é a chamada contrapositiva):
p.s: a negação de ≤ é > e a negação de < é ≥.
b> 4 -> |a| ≥ 3 (não tem nas alternativas)
# Nega a 1ª troca por ‘ou’ e repete a 2ª:
|a| ≥ 3 ou b ≤ 4 (não
tem nas alternativas)
O que faremos? Usaremos a nossa primeira tentativa “b> 4 -> |a| ≥
3” usando a segunda regra: “nega a 1ª troca por ‘ou’ e repete a 2ª”:
b> 4 -> |a| ≥ 3 daí
teremos: b≤ 4 ou |a| ≥ 3 letra
E)
-
Veja o vídeo que gravei com a resolução dessa questão:
https://youtu.be/SyKKdnlS3fo
Professor Ivan Chagas
-
Não entendi pq a letra c não está certa tb.
-
A negação de ( Se... então) é . Mantém1 parte (e) NEGA segunda parte: logo..
A< 3 mantém........ NEGA (b ≤ 4 )
logo fica igual a alternativa c.
A<3 e b > 4
Podem fazer aí a negação de se então ..
Só tem uma coisa . A resposta está invertida lá na questão:
B> 4 e a< 3 . Se isso for errado então é por isso.. Mas que b é menor que quatro e a é menor que 3 Tá certo sim. Ao meu ver
-
Temos uma condicional p→q no enunciado, onde:
p = |a| < 3
q = b ≤ 4
Sabemos que as proposições ~q→~p e “~p ou q” são equivalentes àquela do enunciado. Note que:
~p = |a| ≤3
~q = b > 4
Assim,
~q→~p: se b > 4, então |a| ≤3
e
~p ou q: |a| ≤3 ou b ≤ 4
Temos esta última opção na alternativa E.
Resposta: E