-
x, y e z é a quantidade de cartas para cada bairro e T o total de cartas
x = T - 30
2
y = 1 [ T - ( T - 30 ) ] + 70
3 2
Z = 180
Assim temos;
T = x + y + z
Agora substituimos os valores das incógnitas, deixando apenas o valor de T
T = T - 30 + 1 [ T - ( T - 30 ) ] + 70 + 180
2 3 2
T = T - 30 + 1 [ T - ( T -60 )] + 250
2 3 2
T = T - 30 + 1[ 2T - T + 60 ] + 250
2 3 2
T = T - 30 + 1[ T + 60 ] + 250
2 3 2
T = T - 30 + T + 60 + 250
2 6
T = T + T + 60 + 250 -30
2 6
6T = 3T + T + 60 + 6(220)
6T - 4T = 60 + 1320
2T = 1380
T = 690
ou seja, um valor entre 680 e 700
-
Não entendi o cálculo acima!
-
Por que [T-(T/2-30)] virou repentinamente [T-(T/2-60)]?
-
existe a possibilidade de fazer escolhendo os resultados.
a) coloque um valor intermediario. 690
690 /2 = 345 - 30 = 315
x= 315
315 - 690 = 375...divide por tres e soma mais 70 como informado
y = 195
x+y= 510 - 690 = 180.
certim!!
espero ter ajudado!!
-
Só vou explicar o que a Jozy fez, e seguimos com o mesmo raciocínio dela!
Veja bem, você tem todas as informações de que precisa:
Vamos chamar de “C” as correspondências.
1°) Ao bairro X foi destinada metade das correspondências recebidas na agência menos 30 correspondências. Transformando na linguagem matemática: a agência de correspondências entregou metade do total de correspondências é o mesmo que c/2 menos 30, ou seja, c/2 – 30;
2°) ao bairro Y foi destinada a terça parte das correspondências restantes, isto é, depois de retiradas as do bairro X, e mais 70 correspondências. Veja bem:
Tem um total de correspondências = C
Desse total de correspondências você tira o que foi enviado ao bairro X (c/2 – 30). Então você tem um total de C menos o que foi entregue ao bairro X, ou seja, c – (c/2 – 30), mas foi entregue a 1/3 parte das correspondencias restantes (o resto será o mesmo que o total de cartas inicial menos as cartas que foram entregue ao bairro x), o que já mudaria para 1/3 [c – (c/2 – 30)]. Além disso foram entregues mais 70 correspondências, então teremos 1/3 [ c – (c-2/30)] + 70
3°) ao bairro z foram entregue 180 correspondências.
Se o examinador quer saber o total de correspondências é só somar tudo:
C (total de cartas) = c/2 – 30 [ c – (c/2 – 30)] + 70 + 180
E é o mesmo calculo que a Jozy fez.
-
Montando
a equação abaixo de acordo com o enunciado, onde C (de cartas) será nossa variável:
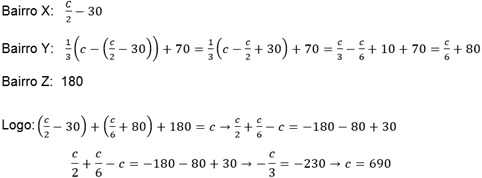
Então, O total de correspondências
recebidas, nesse dia, na agência dos Correios da cidade Alfa foi 690.
Letra
A.
-

-
Z = 180
X + Y + Z = C
X = C/2 - 30; então Y + Z = C/2 + 30
Ou seja, após retirar X restou C/2 + 30
Y = 1/3.(C/2+30) + 70
Então, substituindo os valores de Y e Z na expressão destacada, temos:
1/3.(C/2+30) + 70 + 180 = C/2 + 30
C/6 + 10 + 250 = C/2 +30
C/2 - C/6 = 230
2C/6 = 230
2C = 1380
C = 690
-
T = T - 30 + 1 [ T - ( T -60 )] + 250
2 3 2
T = T - 30 + 1[ 2T - T + 60 ] + 250
2 3 2
Não entendi essa parte da resolução da Josy
-
X = [ C/2 - 30]
Y = [C - (C/2 - 30)]/3 + 70
Z = 180
C = X + Y + Z
C = (C/2 - 30) + (C/3 - C/6 +10 + 70) + 180
C - C/2 - C/3 + C/6 = 230
(7C - 5C)/6 = 230
2C = 6 x 230
C = 690