Questão Q24015

Question

Tr&ecirc;s dados comuns e honestos ser&atilde;o lan&ccedil;ados. A probabilidade de que o n&uacute;mero 6 seja obtido mais de uma vez &eacute;

Answer

Alguém conhece outro jeito de resolver essa?!

Answer

Pede-se a probabilidade que número 6 seja obtido mais de uma vez, portanto:1.Pode sair duas vezes5/6 x 1/6 x 1/6 (sendo 1/6 a probabilidade de sair o "6" e 5/6 a probabilidade de sair um número qualquer tirando o "6") x Permutação de 3 com repetição de 2 (isto pq o número "6" pode sair em qualquer ordem e o 6 se repete duas vezes) TEMOS: 5/6 x 1/6 x 1/6 x 3 = 15/2162. Pode sair as três vezes. 1/6 x 1/6 x 1/6 = 1/216Somando as duas probabilidades temos: 15/216 + 1/216 = 16/216Não se se ficou claro, mas é a forma como faço este tipo de questão.

Answer

Pode ser aplicada a fórmula da LEI BINOMIAL:        ...............................k..........n-kP(E)= ___n!___  . ( P ) . (1-P)     ............k!.(n-k)!onde,n= 3, quantidade de vezes que os dados são lançados;k= 2 e 3, número 6 obtido mais de uma vez. (pode acontecer ao jogar dois dados ou três dados)p= probabilidade de ocorrer o evento (1/6)para k=2;                     P¹(E)= ____3!____ .(1/6)².(1-1/6)³-² = 15/216..............2!.(3-2)! para k=3;P²(E)= ____3!___ .(1/6)³.(1-1/6)³-³ = 1/216.............3!.(3-3)!P(E)= P¹(E)+ P²(E)= 15/216 + 1/216 = 16/216 (letra d)

Answer

P (número 6 nenhuma vez) = 5/6 . 5/6 . 5/6 = 125/216 (restam 5 dos 6 números que poderão aparecer!)

P (número 6 uma vez) = 3 . (1/5 . 5/6 . 5/6) = 75/216 (pode acontecer o número 6 em 3 oportunidades: na 1ª, na 2ª, ou na 3ª jogada. Por isso, precisamos multiplicar o resultado dos dados por 3)

Então:

P (número 6 mais de uma vez) = 1 – [P (número 6 nenhuma vez) + P (número 6 uma vez)]

P = 1 – [125/216 + 75/216]

P = 1 – 200/216

P = 216/216 – 200/216

P = 16/216

Resposta correta: letra D.

fonte: http://beijonopapaienamamae.blogspot.com.br/2010/04/dia-16-de-abril-questao-106.html

Answer

Três dados comuns e honestos serão lançados. A probabilidade de que o número 6 seja obtido mais de uma vez é: A probabilidade de que seja obtido 2 vezes mais a probabilidade de que seja obtido 3 vezes. Usando a distribuição binomial de probabilidade:

$f(k;n,p)={n\choose k}p^k(1-p)^{n-k}\,$

Acha-se a probabilidade de que seja obtido 2 vezes:

$f(2;3,\frac{1}{6})={3\choose 2} imes\left(\frac{1}{6} ight)^2 imes\left(1-\frac{1}{6} ight)^{3-2}\,$

$=\frac{3!}{2!\cdot\left(3-2 ight)!}\,\! imes\frac{1}{36} imes(\frac{5}{6})^{1}\,$

$=\frac{3 imes2!}{2!\cdot\left(1 ight)!}\,\! imes\frac{1}{36} imes\frac{5}{6}\,$

$=\frac{3}{1} imes\frac{1}{36} imes\frac{5}{6}=\frac{15}{216}=\frac{5}{72}\,$

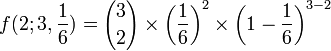
Agora a probabilidade de que seja obtido 3 vezes:

$f(3;3,\frac{1}{6})={3\choose 3} imes\frac{1}{6}^3 imes(1-\frac{1}{6})^{3-3}\,$

$=\frac{3!}{3!\cdot\left(3-3 ight)!}\,\! imes\frac{1}{216} imes(\frac{5}{6})^{0}\,$

$=\frac{3!}{3!} imes\frac{1}{216} imes1\,$

$=1 imes\frac{1}{216} imes1=\frac{1}{216}\,$

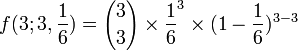
Assim, a resposta é:

$=\frac{15}{216}+\frac{1}{216}=\frac{16}{216}\,$

Answer

Vamos tentar pensar mais objetivo com essa questão.

Existem 4 possibilidades de a premissa do enunciado acontecer:

Tirar 6 nos 3 dados; ------> 1/6 * 1/6 * 1/6 = 1/216

Tirar 6 no 1º e 3º dado; -------> 1/6 * 5/6 * 1/6 = 5/216

Tirar 6 no 1º e 2º dado; ---------> 1/6 * 1/6 * 5/6 = 5/216

e

Tirar 6 no 2º e 3º dado; ---------> 5/6 * 1/6 * 1/6 = 5/216

Soma-se as alternativas e obtem-se o seguinte resultado: 16/216

Letra D

Answer

Só vim entender mesmo com Daniel Aleixo

Answer

Probabilidades:

P ("ser 6") = 1/6

P ("não ser 6) = 5/6

Como ele quer a probabilidade do nº 6 ser encontrado mais de uma vez, a ocorrência deste fato nenhuma vez ou uma vez não nos interessa. Sendo assim, o conjunto de probabilidades fica assim:

Ocorrendo duas vezes:

S ; S ; N = 1/6 * 1/6 * 5/6 = 5/216

S ; N ; S = 1/6 * 5/6 * 1/6 = 5/216

N ; S ; S = 5/6 * 1/6 * 1/6 = 5/216

Ocorrendo 3 vezes:

S ; S ; S = 1/6 * 1/6 * 1/6 = 1/216

Como são 3 possibilidades de ocorrência de 2 nº 6, e 3 possibilidades de ocorrência do nº 6, multiplica suas probabilidades por 3, logo:

5/216 * 3 = 15/216

1/216 * 3 = 1/216

Como se trata de um evento união (ou um, ou outro), P( 2 U 3 ) = 15/216 + 1/216 = 16/216!

Answer

A probabilidade de que o nº 6 seja obtido mais de uma vez é de

S = 6

N = demais números

1º possibilidade:

S S N = 1/6 * 1/6 * 5/6 = 5/216

ou

S N S = 1/6 * 5/6 * 1/6 = 5/216

ou

N S S = 5/6 * 1/6 * 1/6 = 5/216

MMC = 15/216

2º possibilidade

S S S = 1/6 * 1/6 * 1/6 = 1/216

15/16 + 1/16 = 16/216

Answer

Mas Rafael, como surge esse 216/216?

Answer

_____+______+______==> 06

1º 2º 3º

Na 1ª opção temos (1, 2, 3, 4) opções

Na 2ª opção temos (1, 2, 3, 4) opções

Na 3ª opção temos Sobrou apenas uma possibilidade

4*4*1==> 16

6*6*6==>216

16/216

Answer

são 216 possiveis resultados, as chances de todos os 3 dados terem o número 6 seria de 36/216, então como as chances de dois de 3 dados terem o número 6 é menor do que de os 3 terem o número 6?

Answer

Possibilidades:

a)dados 1 e 2 saírem 6

b)dados 1 e 3 saírem 6

c)dados 2 e 3 saírem 6

d)dados 1,2 e 3 saírem 6

Calculando:

probabilidade de ocorrer a: prob (dado 1 sair 6) =1/6 *prob (dado 2 sair 6)= 1/6 *prob (dado 3 não sair 6) = 5/6

probabilidade a = 1/6*1/6*5/6 = 1/216

-------------------------------------------------------------

Probabilidade de ocorrer b e c é o mesmo raciocínio. Logo,

probabilidade b = 1/216 probabilidade c= 1/216

----------------------------------------------------------------------

Probabilidade de ocorrer d: prob (dado 1 sair 6) =1/6 *prob (dado 2 sair 6)= 1/6 *prob (dado 3 sair 6) = 1/6

probabilidade d = 1/6*1/6*1/6 = 1/216

-----------------------------------------------------------------

Probabilidade do evento = prob a + prob b + prob c + prob d = 16/216

Answer

Uma forma pratica de pensar:

PRIMEIRO; quantos lances dos dados possível 6 . 6 . 6 = 216

SEGUNDO eventos

1 ; 6 ; 6 primeiro evento

6 ; 1 ; 6 segundo evento 3

6 ; 6 ; 1 terceiro evento

+

2 ; 6 ; 6 primeiro evento

6 ; 2 ; 6 segundo evento 3

6 ; 6 ; 2 terceiro evento

+

3 ; 6 ; 6 primeiro evento

6 ; 3 ; 6 segundo evento 3

6 ; 6 ; 3 terceiro evento

+

4 ; 6 ; 6 primeiro evento

6 ; 4 ; 6 segundo evento 3

6 ; 6 ; 4 terceiro evento

+

5 ; 6 ; 6 primeiro evento

6 ; 5 ; 6 segundo evento 3

6 ; 6 ; 5 terceiro evento

+

6 ; 6 ; 6; último evento 1

(3.5) + 1 = 16 assim 16/216

Answer

d-

1°- total possibilidades: 6*6*6 = 216

________________________________________________________________________________________________________________________________________________

2°- 6 mais 2x. o 6 pode cair 2 ou 3 vezes

________________________________________________________________________________________________________________________________________________

3°- o 6 caindo 2x:

1/6 * 1/6 * 5/6= 5/216.

(POR QUE 5/6? PORQUE SO ESTAMOS CONSIDERANDO SE O 6 CAIR 2 VEZES. SE AS 2 PRIMEIRAS SERAM 6, É NECESSARIO Q A TERCEIRA SEJA QUALQUER N° MENOS 6)

________________________________________________________________________________________________________________________________________________

4°- a combinacao 1/6 * 1/6 * 5/6 pode ser qualquer 1 das 3 ordens. logo:

5/216*3= 15/216

________________________________________________________________________________________________________________________________________________

5°. agora considerar quando cair 6 3x.

1/6* 3 = 1/216.

________________________________________________________________________________________________________________________________________________

6° somam-se as possibilidades: 15/216 + 1/216 = 16/216. a questao nao exige simplificacao de fracoes. entao R: 16/216

Answer

Pessoal vou fazer de um jeito bem explicado, porque os comentário aqui tá uma confusão total, vamos por passos.

-> Temos 3 dados que a princípio serão lançados 1 de cada vez;

-> Temos de analisar os dados saindo "6" nos 3 lançamentos (mais de 1 vez);

-> Temos de analisar os dados saindo "6" em 2 lançamentos somente (mais de 1 vez);

1) Aqui vamos considerar que irão sair "6" em todos os lançamentos

# 1º Lançamentos temos: 1/6 (1 chance em 6);

# 2º Lançamentos temos: 1/6 (1 chance em 6);

# 3º Lançamentos temos: 1/6 (1 chance em 6);

# Cálculo: 1/6 * 1/6 * 1/6 = 1/216

2) Aqui vamos considerar que irão sair "6" em somente 2 lançamentos;

Obs: Considerando que não vai sair o "6" no 1º lançamento

# 1º Lançamentos temos: 5/6

-> Corresponde a probabilidade de não sair 6, ou seja 5/6 (5 chances em 6), pois não queremos que saia o "6";

# 2º Lançamentos temos: 1/6 (1 chance em 6, pois queremos que saia o "6");

# 3º Lançamentos temos: 1/6 (1 chance em 6, pois queremos que saia o "6");

# Cálculo: 5/6 * 1/6 * 1/6 = 5/216

3) Aqui vamos considerar que irão sair "6" em somente 2 lançamentos;

Obs: Considerando que não vai sair o "6" no 2º lançamento

# 1º Lançamentos temos: 1/6 (1 chance em 6, pois queremos que saia o "6");

# 2º Lançamentos temos: 5/6

-> Corresponde a probabilidade de não sair 6, ou seja 5/6 (5 chances em 6), pois não queremos que saia o "6";

# 3º Lançamentos temos: 1/6 (1 chance em 6, pois queremos que saia o "6");

# Cálculo: 5/6 * 1/6 * 1/6 = 5/216

4) Aqui vamos considerar que irão sair "6" em somente 2 lançamentos;

Obs: Considerando que não vai sair o "6" no 3º lançamento

# 1º Lançamentos temos: 1/6 (1 chance em 6, pois queremos que saia o "6");

# 2º Lançamentos temos: 1/6 (1 chance em 6, pois queremos que saia o "6");

# 2º Lançamentos temos: 5/6

-> Corresponde a probabilidade de não sair 6, ou seja 5/6 (5 chances em 6), pois não queremos que saia o "6"

# Cálculo: 5/6 * 1/6 * 1/6 = 5/216

5) Cálculo geral das probabilidades:

# TOTAL: 1/216 + 5/216 + 5/216 + 5/216 = 16 / 216

Obs: Se os senhores ainda não entenderem manda mensagem aqui pra mim mesmo.

Answer

Estranho!

São três dados. A sequência é irrelevante, a resposta deveria ser 6/216

Agora, se fosse apenas 1 dado, jogado por três vezes, aí sim seria 15/216

Vida que segue...

SóProvas

Continue usando...

O que está incluso