-
Alguém poderia explicar, por favor?
-
Leia com calma a questão.
O exercício pede conhecimento de média aritmética ponderada (lembra-se dos pesos)
Feira de Santana = FS;
Salvador S
E = menor média aritmética entre as distâncias percorridas.
D = Distância entre as cidades.
Observando os pesos, chamarei D de 6KM.
Letra A - Gabarito
FS andam 6KM e S andam 0KM:
3fs + 6s / 3+6 = 3.6+6.0/3+6 >> 18+0/ 9 = 2km. (esta é a menor média)
As demais são incorretas:
Letra B
FS andam 0KM e S andam 6KM:
3.0+6.6/3+6 >> 0+36/9 >> 4KM
Letra C
FS e S andam 3KM:
3.3+6.3/3+6 = 9+18/9 >> 27/9>> 3KM
Letra D:
FS andam 4KM; S andam 2KM
3.4+6.2/3+6 >> 12+12/9 >> 24/9 >> 2,7KM
Letra E:
3.2+6.4/3+6 >> 12+12/9 >> 24/9 >> 2.7KM
-
Letra E:
3.2+6.4/3+6 >> 12+12/9 >> 24/9 >> 2.7KM
Não entendi a conta nessa letra, como 3.2 deu 12?
Fazendo como se desse 6, o resultado tbm é 2. Alguém explica?
-
Minha resolução (difere da do colega, mas cheguei à resposta):
Bahia
FS(3)-------------------D------------------------S(6)
Vamos supor que D seja igual a 1, para facilitar os cálculos.
Distância total é a distância que todos os amigos percorreram somadas.
Média aritmética é a distância total dividida por 2.
a) 6S percorrem 0 e 3FS percorrem 1 -> distância total = 3 -> média = 1,5
b) 6S percorrem 1 e 3FS percorrem 0 -> distância total = 6 -> média = 3
c) 6S percorrem 0,5 e 3FS percorrem 0,5 -> distância total = 3 + 1,5 = 4,5 -> média = 2,25
d) 6S percorrem 0,333... e 3FS percorrem 0,666... -> distância total = 2 + 2 = 4 -> média = 2
e) 6S percorrem 0,666... e 3FS percorrem 0,333... -> distância total = 4 + 1 = 5 -> média = 2,5
A menor média corresponde à letra "a" (ponto de encontro em Salvador). Logo, ela é o gabarito.
-
Ricardo seu meio de fazer é o mais prático, mas se vc supuser que D = 3 fica mais fácil que aí não vai ter número quebrado nas alternativas E e D
-
distancia de FS a salvador irei chamar de D , X = (Distancia de FS ao ponto de encontro / D )
logo a média = (3.X + 9.(1-X)) / 12.
média = (3X+ 9 - 9X)/12 .... (9-6X)/12
logo a menor média possível é quanto maior for o X,o Maior valor possivel de X é 1, assim a distancia de FS ao ponto de encontro tem que ser D.
assim o melhor ponto de encontro é a cidade de Salvador.
-
Distância = 10 x 3 (quantidade mínima de pessoas se locomovendo até salvador) = 30
-
Vamos ter que calcular a média ponderada nessa questão. Vamos supor que a distância entre Salvador e Feira de Santana (ponto D) seja de 110 km. Analisando então cada alternativa:
A)

Logo, 3 pessoas vão saí de FS até Salvador, enquanto que as 6 pessoas que moram em Salvador terão deslocamento zero, assim:
Mp = (3 x 140 + 6 x 0) / (3 + 6) ≈ 46,7
B)
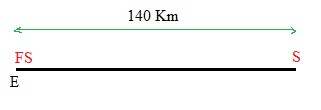
Logo, 6 pessoas vão saí de Salvador até FS, enquanto que as 3 pessoas que moram em FS terão deslocamento zero, assim:
Mp = (3 x 0 + 6 x 140) / (3 + 6) ≈ 93,3
C)
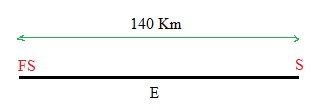
Logo, 6 e 3 pessoas vão saí de Salvador e de FS respectivamente até a metade do caminho, assim:
Mp = (3 x 70 + 6 x 70) / (3 + 6) = 70
D)
Se D = 140Km então D/3 ≈ 47Km, logo:
Mp = (3 x 47 + 6 x 47) / (3 + 6) = 47
E)
O mesmo cálculo da alternativa (D). Mp = 47
Assim, o encontro de modo que a média aritmética das distâncias percorridas por cada um deles desde o local onde moram até o local do encontro seja a menor possível, terá que ser em Salvador.
Resposta: Alternativa A.
-
Gabarito A
Fiz assim:
Dos 9 amigos
3 moram em Feira de Santana = FS
6 moram em Salvador = SA
Eles desejam escolher um local E para o encontro 3FS________E________6SA
D a distância rodoviária, em quilômetros, entre Salvador e Feira de Santana FS_______________SA
Deseja saber a média aritmética das distâncias percorridas por cada um deles desde o local onde moram até o local do encontro seja a menor possível.
Irei atribuir a E o valor 1, e D o valor 1.
Para Feira de Santana
3 FS - D (Distância) = E (Ponto de Encontro)
3 FS = E + D
3 FS = 1 +1
3 FS = 2
FS = 2/3
FS = 0,6
Para Salvador
6 SA - D = E
6 SA = E + D
6 SA = 1+1
6 SA = 2
SA = 2/6
SA = 0,3
Então temos que SA = 0,3 e FS=0,6, ou seja SA menor que FS.
-
O erro dessa questão: quem tem 11 amigos diferentes?
-
Minha resolução:
Chamarei a distância entre Feira de Santana e E de FE e entre Salvador e E de SE.
A média é: M = 6SE + 3FE / 9 = 2SE + FE / 3
SE = D - FE, substituindo esse termo na equação da média fica:
2(D - FE) + FE / 3 = 2D - FE/3. Logo, quanto maior a distância FE (entre Feira de Santana e o ponto E), menor a média. A menor média possível seria com o maior FE possível, o que significa o ponto E estar em Salvador.
Fazendo a mesma coisa mas ao invés de substituir o SE, substituindo o FE:
(só pra garantir)
FE = D - SE, substituindo na equação da média fica:
M = 2SE + (D - SE)/ 3 = SE + D / 3. Logo, a menor média é com o menor SE possível, a menor distância entre Salvador e o ponto E, ou seja, SE = 0.