-
Alguém me explica o gabarito dessa questão!
-
Concurseiro do senhor, eu também estou surpresa com esse gabarito.
Uma vez que 70 pessoas foram entrevistadas.
30 (Graviola)
50 (açaí).
Bem, somando os valores totalizam 80.
70 - 50 = 20
70 - 30 = 40
70 - 60 (pessoas que gostam dos dois) = 10
Amigos, baita dúvida, se puderem ajudar... Serei eternamente agradecida.
Abraços.
Força.
-
Pelo que pude entender, depois que também errei a questão é que:
Entre as 50 pessoas que gostam de açaí - 30 também gostam de graviola.
Então fica:
- 30 pessoas gostam dos dois sabores
- 20 pessoas gostam de apenas açaí
- 30 pessoas gostam de graviola
- 20 não gostam de nenhuma ou não responderam
Em nenhum momento no texto fala que é apenas um sabor. Maldade de leitura de texto!!!!
-
Analisa o diagrama supondo que: 30 gostam de graviola e açai. Com isso fecha o nr da graviola.
então para fechar os 50 que gostam de açaí faltam só 20. Portanto precisa-se apenas de 50 pessoas que gostam das frutas para concluir que 30 graviola e 50 açaí. Então no máximo 20 não precisam gostar de nenhuma... ficam de fora...
-
Pessoal, o raciocínio é o seguinte:
O maior número possível de pessoas que não gostam de nenhum dos sabores é a situação em que todos que gostam de graviola também gostam de açaí, ou seja, os que gostam de graviola são subconjunto dos que gostam de açaí.
Neste caso: 50 gostam de açaí e, pela nossa suposição, desses 50, 30 também gostam de graviola. Como o universo da pesquisa foi 70 pessoas, o máximo de pessoas que não gostam de açaí ou graviola é 20.
Para confirmarmos, basta arbitrarmos um número maior que 20. Por exemplo (vamos usar 25): se 50 pessoas já responderam que gostam de açaí e eu supor que 25 não gostam de nenhum sabor, o universo pesquisado teria que ser, no mínimo, 75 pessoas - visto que não existe intersecção entre esses dois conjuntos (gostar de açaí e não gostar de nenhum sabor).
-
Resolvi da seguinte forma: qual o maior número de pessoas que podem gostar de açaí e graviola? O maior número é 30, pois assim colocaríamos graviola dentro de açaí (conjunto também é imagem né? então a maior - no sentido de tamanho mesmo - interseção é um grupo dentro do outro). Com isso, já eliminamos as letras "c", "d", e "e" e, por consequência, nos damos conta de que vinte pessoas, no máximo não gostam dos dois. Isso porque se eu aumentar o espaço de pessoas que não gostam de açaí e gostam de graviola, eu terei que, necessariamente diminuir o espaço de pessoas que não gostam de nenhum dos dois.
-
Gijuizzzzzzzzzzzzz amado, essas bancas veem que todas as bancas cobram diagrama de venn dai querem cobrar também, só que não tem capacidade de criar questões válidas, corretas. Essa questão pela lógica pela técnica do diagrama de venn também poderia ser correta a letra C, resolvendo de acordo com o básico de conhecimento em relação a diagramas lógicos. Pois bem a questão informa que 70 foram entrevistados, 30 gostam do sabor de graviola e 50 de açaí. Como o valor total é 70. A quantidade de 30 + 50 = 80 logo a diferença é de 10 que é a interseção dos que gostam de açaí e graviola. Exatamente a letra C gostam dos dois sabores.
-
Concurseira Estudando , vc cometeu um erro. Há vários diagramas possíveis, para as informações dadas. Vou me ater aos q aparecem 10, 20 e 30 q são mencionados nas opções. Desses, somente um possui resposta, com as opções fornecidas. Vou te colocar os dados, monte os respectivos diagramas e vc entenderá a questão.
1º Pessoas q gostam de:
só graviola = 20
só açaí = 40
interseção: gostam de graviola E açaí = 10
não gostam de nenhum dos dois = 0
2º pessoas q gostam de:
só graviola = 10
só açaí = 30
interseção: gostam de graviola E açaí = 20
não gostam de nenhum dos dois = 10
3º pessoas q gostam de:
só graviola = 0
só açaí = 20
interseção: gostam de graviola E açaí = 30 (aqui na verdade há uma relação de inclusão, graviola é um subconjunto de açaí).
não gostam de nenhum dos dois = 20
Se vc montou os diagramas de forma correta é só analisar as opções... a única q atende e resolve o problema é a letra A.
Espero ter ajudado.
-
Concurseira Estudando, analise esse fato: imagina que o conjunto A seja do pessoal que gosta de graviola e o conjunto B do pessoal que gosta de Açaí... e se o conjunto A estivesse contido no conjunto B (todos que gostam de graviola gostassem também de Açaí) então a letra C cai por terra ok? Pegando esse gancho a união do conjunto A com o conjunto B teriam as 50 pessoas, restando no máximo 20 pessoas que não gostariam de nenhum dos dois sucos, logo a resposta correta é a Letra A.
-
O que eu entendi para chegar na letra A: é que em NENHUM momento do texto ele diz que um grupo de pessoa diz que GOSTA DOS DOIS SABORES... Nós que deduzimos isso, porque fomos pelo raciocínio básico!
ou seja,
do total de 70 pessoas entrevistadas 50 gostam, de pelo menos um tipo de suco! Dentro dessas 50 pessoas, 30 gostam dos dois tipos. Sobram então 20 pessoas que não gostam de nenhum deles!
Conta:
(Açaí + Graviola) 50 + 20 (não gostam de nenhum sabor) = 70 entrevistado!
-
Que loucura essa questão -_-
-
De acordo com o enunciado, não existe
nenhuma intercepção entre os dois grupos, mas isso não significa que dos 50
entrevistados que gostam de Açaí, não gostam de graviola. Uma vez que ao
fazermos a soma de 50 + 30 = 80, ou seja, obrigatoriamente tem que existir um
público que goste dos dois ao mesmo tempo. Fazendo o diagrama de Venn adequado:
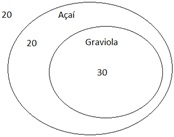
Logo,
no máximo vinte não gostam de graviola nem de açaí. Resposta correta letra A.
-
Não entendi essa questão :/, queria entender a lógica de ser a A.
-
Gente, essa questão é muito simples. Se 50 pessoas gostam de açai e 30 gostam de graviola, o máximo que pode ter de interseção entre açai e graviola é 30. Nesse caso,fica 30 açai E graviola, e 20 só açai (50-30), totalizando 50. Como são 70 pessoas entrevistadas, o máximo de pessoas que podem não gostar de nenhum dos dois é 20 (70 - 50). Acho que ficou confuso, mas com essas informações façam os conjuntos pra ficar mais claro.
-
Gostam de ambos os sucos: x ; Só gostam de graviola: 30 - x ; Só gostam de açaí: 50 - x ; Não gostam de nenhum: y ; Total: 70.
Como as quantidades de elementos dos conjuntos não podem ser negativas, então x>=0, 30-x>=0, 50-x>=0 e y>=0. Assim, percebe-se que 0<=x<=30 e y>=0.
Além disso, analisando os conjuntos, temos que x + (30-x) + (50-x) + y = 70. Resumindo a equação, y = x - 10.
Substituindo os limites de x na equação (0 e 30), temos que y estaria entre -10 (x=0) e 20 (x=30). Como y>=0, o ponto x=0 e y=-10 não é válido. Substituindo y=0 na equação, conclui-se que o limite mínimo de x seria 10. Caso a explicação utilizando as equações não tenha sido suficiente, traçar o gráfico da equação y = x - 10 e analisar o comportamento da função.
Assim, a única alternativa que se enquadra nas condições (10 a 30 pessoas gostam de ambos e 0 a 20 pessoas não gostam de nenhum) é a letra A.
-
Analisando de um jeito bem simples...
30 gostam de graviola
50 gostam de acaí .
Supondo que todas as 30 pessoas que gostaram de Graviola também gostaram de Acaí, neste caso soh restaria 20 pessoas que gostaram exclusivamente do Acaí(pois o exercício fala que 50 gostaram de Acaí).
.
Sendo assim totalizaria pelo menos 50 pessoas que gostaram de pelo menos uma das frutas ou seja no máximo 20 pessoas não gostaram de nenhuma.
-
E porque não se usa a intercessão normal? Nada haver essa questão.
-
Eu achei a alternativa C, porem vi 16 comentários na questão, ai já maldei a questão e fiz de novo, e realmente é letra A pela explicação da colega raquel, mas sem sombra de duvidas, na prova eu erraria. ¬¬
-
Essa questão só parece ser bunitinha.. quando na verdade é o cao ! Aff
-
Eu ERREI. Mas, analisando a questão, será necessário estabelecer um PARÂMETRO para não incorrermos mais neste tipo de erro a partir de agora.
Vamos daqui para frente entender que: se o enunciado NÃO INDICAR INTERSEÇÃO, então entenderemos que seja uma UNIÃO, quando teremos que um menor conjunto(G) estará contido dentro do maior conjunto(A), ou seja, TODO G é A.
Colocando os valores nesta ordem de prioridade:
G = 30
SOMENTE A=20 ***** Com isto deixando o total de A = 50
Conjunto dos que não gostam nem de Açaí e nem de Graviola = 20. Este valor fica fora do diagrama.
TOTAL DE ENTREVISTADOS = SOMENTE A + G + Entrevistados que não gostam dos nem de Açaí e nem de Graviola = 70
TOTAL DE ENTREVISTADOS = 20 + 30 + 20 = 70
-
Rapaaz que loucura essa questão!! Eu seguir a lógica dos oitenta entrevistados mas depois é a A a correta?? La ele ...
-
Achei a explicação num vídeo no youtube: https://www.youtube.com/watch?v=ab5xioA0_0s
-
Entrevistados = 70
Gostam de graviola = 30
Gostam de açaí = 50
70 - 30 = 40
70 - 50 = 20
40+20 = 60
Gostam de graviola ou açaí = 80
80 - 60 = 20
Letra (A)
-
O enunciado tem que falar ou isso, ou aquilo, ou os dois.
Se não falar é por que não existe nenhuma intercepção entre os grupos.
-
Questão EXTREMAMENTE mal formulada.
-
Explicação passo a passo com o Cid Moreira:
https://www.youtube.com/watch?v=ab5xioA0_0s
-
FGV né gente......é assim......precisamos ir além para resolver as questões da banca! E, realmente, está correto o raciocínio proposto.
-
A questão não está mal formulada. Ela apenas exige um raciocínio não muito usual para esse tipo de questão.
Temos que a soma dos que gostam de graviola (30) e dos que gostam de açaí (50), que é 80, ultrapassa o número de entrevistados (70). Logo, CERTAMENTE, existe um conjunto intersecção. Chamemos ele de x. O valor mínimo de x é 10, pois então 20 gostarão apenas de graviola, 40 gostarão apenas de açaí e 10 gostarão dos dois sabores, dando a soma o valor exato de entrevistados (70). Percebe agora que, caso x fosse 11, haveria 1 pessoa que não gostaria de nenhum dos dois sabores. O mesmo raciocínio pode ser feito de 12 para 2, 13 para 3, 14 para 4,... Em determinado momento, o x chega ao seu valor máximo, que é 30. Por quê? Por que a intersecção de graviola com açaí jamais poderá ser maior do que o próprio conjunto graviola (no máximo pode ser igual). Assim, se x for igual a 30, o número de pessoas que não gostam de nenhum sabor será 20. GABARITO: A
-
Li todos os comentários e não entendi. Daí eu vi o vídeo e entendi. Vejam o vídeo no youtube. https://www.youtube.com/watch?v=ab5xioA0_0s
-
é o tipo de questão que temos que fazer analisando as opções disponíveis no enunciado.
considerando: açai = A e graviola = G
como 30+50 = 80 > 70, certamente existe um número de pessoas que responderam gostar de A e de G (intersecção)
nº mínimo de pessoas que não gostam de A e nem de G = 0 (posso considerar que todas gostam de alguma fruta)
nº mínimo de pessoas que gostam de A e de G = 10
sendo: B a intersecção de G e A, Z+B+C = 70
B+C = 30 pessoas gostam G
Z+B= 50 pessoas gostam de A
substituindo eu chego aos seguintes resultados: B = 10; Z= 40, C= 20, D (pessoas que não gostam de nenhuma)= 0
nº máximo de pessoas que não gostam de A e nem de G = 20 (se eu considerar que todos que comem graviola também comem açai, eu fico com 30 na intersecção, 20 que comem apenas açai (50-30=20), e me sobram 20 (70-50=20)
nº máximo de pessoas que gostam de A e de G = 30 (pois as pessoas que responderam gostar de G são 30)
-
A ideia é considerar os máximos e mínimos que os conjuntos podem obter.
Na leta A- realmente o máximo é 20, podemos ver isso se considerarmos o caso em que G é subconjunto de A, assim veremos que apenas 50 pessoas gostam de pelo menos um sabor, ou seja, das 70 eu terei no maximo 20 que não gosta de nenhum. Ainda nesse ponto de vista, dá pra perceber que o numero máximo de pessoas que gostam das duas frutas é 30, pois G é subconjunto de A e G tem 30 elementos o que quer dizer que a intesecção de A com G é igual ao conjunto G. Isso torna a alternativa C Incorreta. Se no maximo 30 gostam dos dois sabores, então o caso em que no mínimo 30 gostam dos dois sabores(Letra D) não existe, Mais especificamente o minimo seria 5. na letra E entende-se de mesmo modo que a letra C.
A letra B Está Errada pois o valor mínimo seria 0. para entender isso basta considerar o caso em que a intersecção é 10. vc verá que todos os entrevistados gostam de pelo menos um sabor.
-
Algúem que assistiu o vídeo do youtube ( https://www.youtube.com/watch?v=ab5xioA0_0s),
o prof. mostrou 2 formas possíveis de resolver a questão, então, parece que a questão tem 2 gabaritos. Se houver intersecção, 10 pessoas gostam dos 2, (letra c); se um conjunto for subconjunto de outro, então 20 pessoas não gostam de nenhum, (letra a).
Alguém poderia me esclarecer por que a letra a está mais correta que a letra c?
-
bom dia
a " dica " ( pelo que entendi ) é :
SE NÃO AFIRMAR QUE HÁ AMBOS ( GOSTO DE A E B ) É QUESTÃO DO TIPO - TODO A É B . QUE PODE TER ' SOBRA ' . o NEM A E NEM B .
-
Juliana, o máximo que pode gostar dos 2 sabores é 30. Conjunto Graviola contido no conjunto açaí
-
Olhem a resolução desse professor: https://acasadasquestoes.com.br/simulados/resolver/q39133/teoria-dos-conjuntos-3-matematica-basica-1#.VuwsttIrLIU
-
TOTAL ~~> 70
AÇAÍ ~~> 50
GRAVIOLA ~~-> 30
Perceba que, como a soma de graviola e de açaí ultrapassou 70, é porque necessariamente exitem algumas pessoas que gostam dos dois sabores.
Mas a grande reflexão que a questão exige: Também podem existir pessoas que não gostam de nenhum dos sabores!
Então a situação fica estruturada desta maneira:
X : Gostam dos dois sabores
50 : Gostam de Açaí. Então 50 - X : Gostam SÓ de açaí.
30 : Gostam de Graviola. Então 30 - X : Gostam SÓ de graviola
Y : Pessoas (se existirem) que NÃO gostam de nenhum dos sabores.
Somando tudo, tem que bater com o universo da amostra: 70:
X + (30 - X) + (50 - X) + Y = 70
80 - X + Y = 70
X = 10 + Y
Agora perceba também que são exatamente, como disse o enunciado, 30 pessoas que gostam de graviola. Ora se trinta gostam de graviola, independentemente de gostar só dela ou dela e do açaí também, então não tem como que 31 pessoas gostem dos dois, pois aí passaria dos trinta!
Também sabemos que 10 + Y = X. Ora, como X não pode ser mais de 30, temos a seguinte inequação:
10 + Y < = 30 (lê-se dez x mais y menor ou igual a 30)
Y < = 20
Pronto, Y pode ser no menor ou igual a 20, ou seja, máximo 20! Se Y for maior que 20, então X será maior que 30. Já que X não pode ser maior que trinta então está correta a letra A.
Espero ter ajudado.
-
O que adianta o professor comentar a questão apenas escrevendo? Pra quem não entende, não adianta escrever, escrever.. Matéria como essas devem ser explicadas com vídeos!
Fica a dica Qc!
-
Acredito que as palavras-chaves dessa questão são MÁXIMO e MÍNIMO que estão presentes nas alternativas, quando se pretende analisar o máximo e o mínimo deve se utilizar essa metodologia "Diagrama de Venn aninhado", porque através dela vc poderá concluir o valor máximo de um conjunto e inferir o valor que não pode ser mínimo. Portanto, não acho que ela seja mal formulada.
-
Gente, essa questão não tem mistério.
Não podemos afirmar que no máximo 10 gostam dos 2 sabores, já que ele diz que 30 gostam de graviola e 50 de açai, então o máximo de pessoas que gostam dos 2 sabores são 30, pois em nenhum momento o texto afima que as pessoas só gostam de graviola, ou só de açai, podem muito bem gostar dos 2.
-
Excelente resolução Timóteo Sampaio
-
O choro é livre, a questão é boa. Como 50 + 30 > 70, é óbvio que tem intersecção. A banca não é obrigada a afirmar isso.
Pensem comigo: NO MÁXIMO 30 pessoas gostam de GRAVIOLA E AÇAI. Nesse caso nenhuma pessoa gosta só de graviola, 20 só AÇAI e 20 NENHUM DOS SABORES.
Desenhando fica mais claro.
-
Vejam o comentário do Márcio Bueno - Li todos os comentários e não entendi. Daí eu vi o vídeo e entendi. Vejam o vídeo no youtube.https://www.youtube.com/watch?v=ab5xioA0_0s
Só consegui entender com a explicação do vídeo.
Bons estudos!!!
-
O segredo desse tipo de questão é não confundir com as questões tradicionais de Conjuntos (diagrama de venn).
Nas questões tradicionais de Conjuntos (diagrama de venn), o enunciado diz que todos gostam de alguma coisa ou então diz a quantidade de pessoas que não gostam de nenhuma das duas coisas. Se nesta questão ele falasse isso, a resposta seria letra c) (no máximo) EXATAMENTE dez gostam dos dois sabores.
Mas, a questão não fala nada sobre os que não gostam de nenhum dos dois. Então temos que verificar as possibilidades de máximo e mínimo !!!!!!!!!!!!!
Ou seja, tem que analisar os conjuntos disjuntos (sem interseção) E também quando um está completamente dentro do outro (um contido no outro)!!!!!
Obs: No caso desta questão, repare que é impossível o conjunto ficar disjunto (sem interseção), pois necessariamente teremos que ter uma interseção de no MÍNIMO 10 (80-70) !!!!!!!!!!!
-
Li todos os comentários dessa questão - inclusive, bem elaborada -, muitos deles equivocados, mas todos plausíveis, já que não é uma questão tão usual (demorei entendê-la também). É necessário inferirmos dados do enunciado e "testar" possibilidades, incluindo aí o máximo e mínimo de interseção. Não irei adentrar na resolução, uma vez que Gabriel Prola e Timoteo Sampaio fizeram isso com muita exatidão. Deixarei o link de um problema semelhante a esse, com um nível ainda maior, para que nos acostumemos:
https://www.youtube.com/watch?v=PGYDViDqoCc
-
Essa questão cobra um conhecimento a mais do que um simples diagrama de Ven, pois ele fala em máximo e mínimo, além de ele não informar quantos não gostam de nenhum dos dois sabores.
A alternativa C que causou maior confusão está errada.
Perceba que a intersecção pode ser 30, fazendo dessa forma que a área das pessoas que afirmaram gostar APENAS de graviola, seja zero.
As pessoas que passaram são normais como todos nós! Não desistam, um dia chegaremos lá também!
-
A vida não tá fácil pra ninguém kkkkk coitado dos jornalistas
-
Esta questão é simples quando ele dá o valor de 80 e depois dá o valor total de 70 notamos que o 80 não é proporcional, mas é ele que vai dar a resposta, foi isso que a banca quis nós dizer então é só focar no 70 vamos lá.
30 graviola
50 açaí
então focando no 70 pegamos o valor maior que é o açaí 50 menos o valor da graviola 30:
50 - 30 = 20
é só logica.
-
Paula BI, também cheguei a alternativa "C" com o raciocínio básico de diagramas. Só que a questão vai um pouco mais além de conhecimento básico em diagramas de Venn. Envolve raciocínio lógico e matemático. Também recomendo o vídeo https://www.youtube.com/watch?v=ab5xioA0_0s, como também foi recomendado por outros colegas aqui.
-
Aíííí pai, que essa na prova é uma casca de banana linda