-
Questão simples que pode ser facilmente resolucionada pelo diagrama de Venn!
O total dos funcionários que fizeram alguma escolha é: 90%
Total de A+Total de B= 55% + 75%= 130%......Significa dizer que o que passar de 90% é a interseção. Logo, 130-90= 40 (Ou seja, 40% dos funcionários escolheram os candidatos A e B concomitantemente). Então...
55%-40%= 15% só A
75%-40%= 35% só B.......................Que escolheram apenas um candidato: 35+15=50%
Letra A
até mais!
;)
-
Candidato A = 55; Candidato B = 75; Branco = 10.
A+B+C-(A interseção B) = 100 (pois não há interseção com C - voto em branco)
55+75+10-(A interseção B) = 100
(A interseção B) = 55+75+10-100
(A interseção B) = 40
Funcionários que votaram somente em A = 55-40 = 15
Funcionários que votaram somente em A = 75-40 = 35
Total de funcionários que votaram em apenas um candidato: 15+35 = 50.
-
Fiz da seguinte forma, rapidinho, usando o diagrama de Venn. O total é 100% mas tirei os 10% que não fazem intersecção porque votaram nulo. Então fiquei só com 90% para distribuir entre A, B e A^B. A soma de A e B pelos totais dá 130% (55% de A+ 75% de B). Como eu só tenho 90% para distribuir, subtraí esse valor de 130% o que deu: 40% para a intersecção A^B. Aí foi só tirar esse valor dos 55% de A e dos 75% de B. Ficou 15% e 35%, somando deu 50%.
-
Total = 100%
Votaram = 90%
Não votaram = 10%
Votaram nos 2 candidatos = x%
(55-x) + x + 75-x = 90 (total dos que votaram)
x = 40% = quantidade que votou nos dois candidatos
90% (votaram, no total) - 40% (votaram em dois candidatos)= 50% (escolheram só um)
-
Aqui nesta questão, vamos utilizar o
diagrama de Venn:
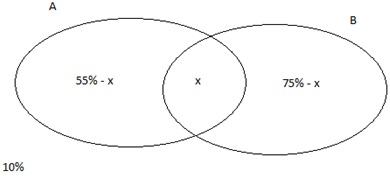
Fazendo-se as contas: 55% - x + x 75% - x +10% = 100%
X =
40%
Assim:
55% - 40% = 15% escolheram apenas o candidato A e 75% - 40%
= 35% escolheram apenas o candidato B, somando teremos: 15% + 35% = 50%
Letra A.
-
Se 10% dos votos foram em branco, 90% dos funcionários votaram em apenas um ou em ambos candidatos.
Se 90% votaram em pelo menos um, então (55%+75%)-90% = 40% votaram em ambos.
Se 40% votaram em ambos, apenas 55%-40% = 15% votaram no candidato A.
Se 40% votaram em ambos, apenas 75%-40% = 35% votaram no candidato B.
Total de funcionários que escolheram somente um candidato = 15%+35% = 50%
-
No caso, ao verificar que somente 10% votaram em branco, percebe-se que 90% votaram pelo menos em um deles. Assim, pode-se concluir que:
* Desses 90%, 75% escolheram o B, então, 15% votaram apenas no A;
* Desses 90%, 55% escolheram o A, então 35% votaram apenas no B;
Portanto, somando-se 15% + 35%, tem-se que 50% votaram em apenas um candidato.
-
conj A = 55 - x
conj B = 75 - x
intersecção x
branco 10
55-x + x + 75 -x + 10 = 100
-x + 140 = 100
x = 40
intersecção 40
conj A = 55 - 40 ->15
conj B = 75- 40 ->35
logo 35 + 15 = 50 resposta A
-
como não vi nenhuma resolução semelhante a minha, então temos:
140(soma de tudo) - 40( excedente) - 55 ( percentual de A) - 10 ( votantes em branco)= 35
140 - 40 - 75 (percentual de B) - 10 = 15
somando se 50%
-
100% - 10% (não votaram) = 90% dos funcionários votaram
55% + 75% = 130% (o excedente dos 90% - interseção - são os funcionários que votaram em ambos candidatos)
140% - 90% = 40% votaram em ambos funcionários
55% - 40% = 15% (votaram somente em A)
75% - 40% = 35% (votaram somente em B)
50% votaram em apenas um candidato.
-
SIMPLES!
TOTAL: 100% NEM A NEM B: 10%
1) ENTÃO, 100 - 10 = 90 % DE PESSOAS QUE VOTARAM EM A OU B
2) PELA FÓRMULA, VAMOS DESCOBRIR A INTERSECÇÃO, OU SEJA, QUEM VOTOU NOS DOIS:
90 = 55 (A) + 75 (B) - X
X = 40% QUE VOTOU NOS DOIS
3) ENTÃO AGORA SUBTRAIA 40 DOS VALORES DE A E B PRA DESCOBRIR QUEM VOTOU APENAS EM A E APENAS EM B:
A: 55 - 40 = 15%
B: 75 - 40= 35%
RESULTADO: 15% + 35% = 50%
-
Pra ficar simples, estabeleça um valor hipotético que represente o total.
-
Gabarito A
A=55
B=75
Nulo=0
A~B= 10-100 = 90
(AUB) = A+B - (A~B)
(AUB) = 55 + 75 - 90
(AUB) = 130 - 90 = 40 votaram em ambos
55% - 40% = 15% Candidato A
Então 35% votaram no candidato B
A+B = 15% + 35%
A+B = 50%
"Retroceder Nunca Render-se Jamais !"
Força e Fé !
Fortuna Audaces Sequitur !
-
Fazendo-se as contas: 55% - x + x 75% - x +10% = 100%
X = 40%
Assim:
55% - 40% = 15% escolheram apenas o candidato A e 75% - 40% = 35% escolheram apenas o candidato B, somando teremos: 15% + 35% = 50%
Professor QConcursos.
-
0,9 = 0,55 + 0,75 - X
X = 0,4 = 40%
A = 55% - 40% = 15%
B = 75% - 40% = 35%
35% + 15% = 50%
-
Como trata-se de porcentagem, o total será 100%.
Se somarmos o que ele aponta no enunciado, teremos que 55% + 75% dará 130%
Com isso, notamos que 30% é a interseção
--> No grupo A, retiraremos esta interseção encontrada acima, onde teremos: 55% - 30% = 25% -->mas ainda teremos que tirar os 10% dos votos brancos, então: 25% - 10% = 15% (guarda esta número aí).
--> No grupo B, retiraremos a interseção encontrada, e ficará: 75% - 30% = 45% --> retiro, também, os 10%, e teremos 35%.
Somando os dois resultados (15% + 35%), que é o que o problema pede (apenas o que votou em um dos candidatos A+B), temos 50%
-
55% = A
75%= B
10% = BRANCO
SENDO ASSIM:
55% +75%+ 10% = 140 LOGO INTERSEÇÃO ( 40 )
OBS: O MAIOR VALOR DA PORCENTAGEM É 100%, LOGO O QUE SOBRA É A INTERSEÇÃO.
55% - 40% =15%
75% - 40% =35%
RESPOSTA:
15% +35% = 50%
-
Quem como eu foi logo apressado na letra B achando que a questão pedia a interseção??? manda like. kkkkk :(
-
Fiz assim:
10% ta fora
Sobram 90%.
Então, peguei os 90% e subtraí por 75% = 15% (só A).
Se o A é 55%, 55 - 15 = 40.
Somando os "somente de um", temos 15 + 35 = 50.
-
https://www.youtube.com/watch?v=mBH6WpLAXko
-
O EXCEDENTE É SEMPRE A INTERSEÇÃO
O TOTAL É 100%
55+75+10=140%
100%-140%=40
A=55-40=15
B=75-40=35
35+15=50%
-
Se 10% votaram nulo, sobra 90%
90% - 55% = 35% de A
90% - 75% = 15% de B
35% + 15% = 50%
-
Eu fiz assim:
A: 100- 55 =45-10= 35
B: 100-75=25-10= 15
Somando 35+15= 50%