-
Am = 3Ac
Ap = 4Ac
Ac/2 = 520 - (Am+Ap-Ac)
Am = Aprovados em Matemática
Ap = Aprovados em Português
Ac = Aprovados no concurso
Logo, Ac = 80.
-
Alguém poderia colocar a resolução ? não estou conseguindo fazer..
-
3x + 4x – x +x/2 = Total de inscritos
Resolvendo a Fração:
3x/1 + 4x/1 -x/1 + x/2
(6x + 8x - 2x + x) / 2 = 13x / 2
13x/2 = 520/1
Multiplicando cruzado: 13x = 520*2
13 x = 1040
x = 1040/13
x = 80
-
Seja A, o total de aprovados, AM, AP e NA os aprovados em matemática e português e o número de candidatos não aprovados em nenhuma das duas provas respectivamente, temos:
Total de inscritos = (AM + AP) - A + NA
Exemplificando pelo diagrama de Venn:
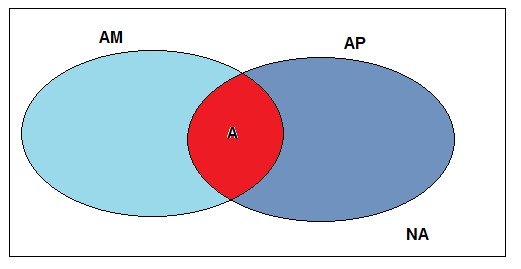
Substituindo os valores dados no enunciado:
Total de inscritos = 3x + 4x – x +x/2 = 520
Multiplicando tudo por 2:
6x + 8x - 2x + x = 1040
13x = 1040
x = 80
Resposta: Alternativa B.
-
X = número de aprovados no concurso
3X = aprovados em Matemática
4X = aprovados em Português
X/2 ou 0,5X= não foram aprovadas em nenhuma disciplina
3x + 4x - 0,5x = 520
X = 80
-
não compreendo porque 0,5x entra na equação com sinal negativo, já que os candidatos não aprovados em nenhuma das disciplinas devem ser contados como inscritos também. Poderiam clarear?
-
Faz o diagrama
Aprovados (M e P) = x
Só M = 3x, mas como pra ser aprovado tem que passar em M, fica M=2x, pois o outo x é a interseção (M e P)
Só P=4x, mas mas como pra ser aprovado tem que passar em P, fica P=3x, pois o outo x é a interseção (M e P)
Não aprovados = 0,5x
Logo, x+2x+3x+0,5x=520 x=80
-
3x+4x + x/2 - x = 520
6x + 8x + x - 2x = 520 ---> 13x = 1040 ----> x = 80
2
-
x+(4x-x)+(3x-x)+x/2 = 520
x+3x+2x+x/2=520
6x+x/2=520
12x/2+x/2 = 520
13x/2=520
13x=520.2
13x=1040
x=1040/13
x=80
-
Se montarmos um diagrama de Venn temos: conjunto M (matemática), conjunto P (português), conjunto intersecção A (aprovados = pertencem a M e a P) e o conjunto N (não aprovados). Logo, 520 = M + P - I + N, já que como A pertence tanto a M como a P, deve ser subtraído para que em M e P só restem os aprovados só em M ou P, mas não em ambos. Com efeito, chamando de a os aprovados no concurso, então M -> 3a, P -> 4a e N -> a/2. Logo:
3a + 4a + a/2 - a = 520
mmc = 2, então:
6a + 8a + a -2a = 1.040
13a = 1.040
Logo: 1.040/13 = 80
R: 80 foram os aprovados no concurso.
-
x= apovados no concurso (M ∩ P)
3x = aprovados em matemática (não necessariamente só em matemática)
4x= aprovados em português ( não necessariamente só em português )
0,5x = não aprovados em nenhuma das duas
2x + 3x + x +0,5x = 520
6,5x = 520
x= 80 => aprovados no concurso
-
Resolvo essa questão aqui nesse vídeo
https://youtu.be/1GmHR7GagsU
Ou procure por "Professor em Casa - Felipe Cardoso" no YouTube =D
-
Vamos considerar dois conjuntos: aquele formado pelos aprovados em matemática e aquele formado pelos aprovados em português. Os aprovados no concurso são aqueles que tiveram sucesso nas duas provas, ou seja, trata-se da interseção entre os dois conjuntos anteriores.
Como o número de candidatos aprovados em matemática é o triplo dos aprovados no concurso, podemos escrever:
n(matemática) = 3 x n(matemática e português)
Como o número de aprovados em português é o quádruplo do número de aprovados no concurso, podemos escrever:
n(português) = 4 x n(matemática e português)
O número de candidatos que não foram aprovados em nenhuma das provas é:
520 - n(matemática ou português)
Esse número é igual a metade dos candidatos aprovados no concurso, ou seja:
520 - n(matemática ou português) = n(matemática e português) / 2
Podemos reescrever essa ultima equação assim:
n(matemática ou português) = 520 - n(matemática e português) / 2
Lembrando que:
n(matemática ou português) = n(matemática) + n(português) - n(matemática e português)
Podemos substituir as expressões que encontramos anteriormente nesta última equação ficando com:
520 - n(matemática e português) / 2 = 3 x n(matemática e português)
+ 4 x n(matemática e português) - n(matemática e português)
520 - n(matemática e português) / 2 = 6 x n(matemática e português)
Multiplicando todos os termos da equação acima por 2, ficamos com:
1040 - n(matemática e português) = 12 x n(matemática e português)
1040 = 13 x n(matemática e português)
n(matemática e português) = 1040 / 13 = 80
Este é o número de candidatos aprovados no concurso.
Resposta: B