-
Pensei que fosse letra A. Fiz da seguinte forma: 3/5=0,6. Transformando em fração será 6/10. Simplificando fica 3/5. Mas no meu entendimento isto seria sobre o total de sucos, não de uma garrafa.
Se alguém puder explicar, agradeço.
-
Patrícia, precipitadamente, tive o mesmo raciocínio q vc e tentando demonstrar ficou a mesma dúvida! Acho que quando ele afirma: serem as garrafas iguais, não está dizendo que têm o mesmo volume. Considerei que cada garrafa tem uma variável "X" de suco. Se são 3 garrafas com essa variável X de volume de suco, então se somadas as quantidades darão 3X de suco por garrafa. Em seguida essa quantidade deve ser distribuída igualmente por 5 pessoas, o que representa 3X/5 de volume de suco por garrafa. Não é necessário saber as quantidades de volume da variável X. Ao relacionar com valores, vejo uma contradição. Imagine que a primeira garrafa contenha 20 ml³ (X1) de suco; a segunda 40 ml³ (X2) e a terceira 60 ml³ (X3). Obedecendo o comando da questão, cada garrafa deve distribuir seu volume igualmente por 5 pessoas. 20/5= 4 ml³; 40/5= 8 ml³; 60/5 = 14 ml³. É óbvio que no final cada uma das 5 pessoas receberão as mesmas quantidades de suco por garrafa, isto é, 26 ml³ para cada uma das 5 pessoas. No entanto, observe que esse valor é maior ( 26ml³) do que o volume da primeira garrafa ou variável X1 (20 ml³). A meu ver, só tem sentido se for considerado o valor total de suco!! Gostaria também da ajuda para entender melhor essa questão!
-
Então Patricia Silva e Rogério Costa. Eu fiz assim:
Imaginei 03 garrafas com (um valor aleatório) de 100ml cada, Total=300ml (as 03 garrafas);Depois, dividi os 300ml paras as 05 pessoas, (300/5) resultando
60ml para cada;
A) 3/5 do total dos sucos, seria (300/5) = 60 * 3 = 180ml (errada);
C) 5/3 do total dos sucos, seria (300/3) = 100 * 5 = 500ml (errada);
D) 5/3 do suco de uma garrafa, seria (100/3) = 33 * 5 = 165ml (errada);
E) 6/15 do total dos sucos, seria (300/15) = 20 * 6 = 120ml (errada);
B) 3/5 do suco de uma garrafa, seria (100/5) = 20 * 3 = 60ml (CORRETA)
-
Fiz da seguinte forma:
Cada uma das 5 pessoas recebeu 1/5 de cada garrafa, ou seja, 1/5 da 1ª garrafa, 1/5 da 2ª garrafa, e 1/5 da 3ª garrafa. Soma todos e vai encontrar quanto cada um recebeu: 1/5+1/5+1/5= 3/5 ( Ao meu ver isso é em relação ao todo, e não a uma garrafa)
-
Meu raciocínio foi o seguinte: como a questão é de múltipla escolha, vamos utilizar as respostas que ela dá para começar a pensar e vamos eliminando.
Ok, eu tenho 3 sucos para dividir entre 5 pessoas (3/5 ou três para cinco -- essa fração corresponde ao total dos sucos); se eu fracionar cada suco em três "pedaços", eu terei 9 "pedaços" de suco (3 x 3) para dividir entre 5 pessoas ou nove frações de suco para dividir entre cinco pessoas (9/5 ou nove para cinco -- mais uma vez, corresponde ao total de sucos). Olhando para as alternativas, nenhuma se encaixa nisso...
E se eu fracionar meu suco em cinco "pedaços"? Daí eu terei 15 "pedaços" de suco (3 x 5) para dividir entre 5 pessoas, ou seja, quinze frações de suco para dividir entre cinco pessoas (15/5 ou 15 para cinco -- mais um vez, total de sucos). Opa! 15/5 = 3. Ou seja, dividindo cada garrafa em cinco "pedaços", cada uma das pessoas ficará com 3 "pedaços" de garrafa.
Alternativa correta, "b": cada uma recebeu 3/5 do suco de uma garrafa.
Espero que compreendam o raciocínio!
-
eu errei mas logo percebi que não é 3/5 em relação ao total dos sucos pois( o todo, ou seja o total do suco =1)
-
Analisando a questão,
Vamos supor que cada garrafa contenha X litros,
assim se eu tenho 3 garrafas, então o total será de 3X.
Temos que dividir
igualmente entre 5 pessoas:
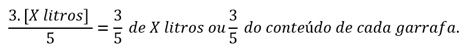
RESPOSTA: (B)
-
Fiz o cálculo da seguinte forma:
Imageinei cada garrfa a 100ml cada. Logo, o total é 300ml. Depois dividi por 5 e descobri 60ml. Esse é o valor que cada pessoa irá receber. Considerando a letra A), 3/5 do total de sucos daria e seguinte expressão: 300mlx3/5. O resultado é 180ml. Isso não corresponde ao valor que cada um irá receber (60ml). Por outro lado, a alternativa B) confere com o resultado, já que 3/5 do suco de uma garrafa corresponde a 100mlx3/5 = 60ml.
Espero ter ajudado na questão. Bon estudos!
-
Patricia Silva
"Pensei que fosse letra A. Fiz da seguinte forma: 3/5=0,6. Transformando em fração será 6/10. Simplificando fica 3/5. Mas no meu entendimento isto seria sobre o total de sucos, não de uma garrafa.
Se alguém puder explicar, agradeço."
Você partiu de 3/5 e voltou para 3/5. Não houve nada de efetivo nessa conta. Os 3/5 não poderiam ser sobre o total de suco, haja vista o que cada um recebeu do total só pode ser 1/5.
Rogério Costa
".... Acho que quando ele afirma: serem as garrafas iguais, não está dizendo que têm o mesmo volume. Considerei que cada garrafa tem uma variável "X" de suco. Se são 3 garrafas com essa variável X de volume de suco, então se somadas as quantidades darão 3X de suco por garrafa. (...). Imagine que a primeira garrafa contenha 20 ml³ (X1) de suco; a segunda 40 ml³ (X2) e a terceira 60 ml³ (X3). Obedecendo o comando da questão, (...). 20/5= 4 ml³; 40/5= 8 ml³; 60/5 = 14 ml³. É óbvio que no final cada uma das 5 pessoas receberão as mesmas quantidades (...), isto é, 26 ml³ para cada. valor é maior ( 26ml³) do que o volume da primeira garrafa. A meu ver, só tem sentido se for considerado o valor total de suco!! Gostaria também da ajuda para entender melhor essa questão!"
A premissa contém um erro de lógica e de interpretação: primeiro: se os volumes fosse diferentes, com valor X, a soma não poderia ser 3X, aliás, se fosse diferentes nem poderiam ser todos chamados de X. segundo: o enunciado disse que são garrafas idênticas. Daí sua premissa errônea gerou os resultados errados a que você chegou.
RENATO MAURIZ
"Fiz da seguinte forma:
Cada uma das 5 pessoas recebeu 1/5 de cada garrafa, ou seja, 1/5 da 1ª garrafa, 1/5 da 2ª garrafa, e 1/5 da 3ª garrafa. Soma todos e vai encontrar quanto cada um recebeu: 1/5+1/5+1/5= 3/5 ( Ao meu ver isso é em relação ao todo, e não a uma garrafa)"
Quando você soma os três 1/5, você está somando frações de inteiros diferentes, por isso a distorção no resultado. A soma correta seria 1/5 de 1/3 somado, já que cada 1/5 se refere ao 1/5 de uma garrafa, e uma garrafa é 1/3 do total. Assim sua resposta seria 9/15 (que é o mesmo que 1/5) do total e não 3/5 do total. Note que 1/5 do total é a resposta óbvia, já 3/5 não faz sentido, já que é um valor acima da metade, impossível tal resultado (aqui você já nota que a letra A está descartada).
RESOLVENDO A QUESTÃO POR RACIOCÍNIO
(POR ÁLGEBRA JÁ ESTÁ RESOLVIDA PELO PROFESSOR E POR OUTROS COLEGAS)
3 GARRFAS DIVIDAS POR 5 PESSOAS. SE FOSSEM 6, CADA UMA FICARIA COM METADE DE CADA GARRAFA. COMO SÃO SÓ 5, ENTÃO CADA PESSOA VAI FICAR COM UM POUCO MAIS QUE A METADE.
LETRA B) 3/5 DE CADA GARRAFA, ÚNICA OPÇÃO EM QUE CADA UM RECEBE UM VALOR A MAIS QUE A METADE.
As outras são todas absurdas:
a) 3/5 do total dos sucos.Mais da metade do total, não dá nem pra 2 pessoas...
c) 5/3 do total dos sucos. Maior que o inteiro, absurdo.
d) 5/3 do suco de uma garrafa. Quase 2 garrafas pra cada...
e) 6/15 do total dos sucos. 2/5 não, teria de ser 1/5