-
O problema quer as jogadas que somem 6, 7, 8 e 9. Deve-se excluir os valores repetidos, ou seja, só considera uma vez, por exemplo, a soma 1 e 5 (não considera 5 e 1). Espero que o quadro abaixo ajude a entender:

-
Mas por que sobre 21...nao seria sobre 20?
-
21 = número de grupos ( (1,1) , (1,2), (1,4).....) possíveis formados nos lançamentos de dois dados de forma simultânea, sem as suas repetições ( (2,1), (4,1).....)
Exemplo. (2,1) ou (1,2), não fazem diferença para o lançamento simultâneo, neste caso. Conta-se como o mesmo.
São eles: (1,1),(1,2), (1,3), (1,4), (1,5), (1,6), (2,2), (2,3), (2,4), (2,5), (2,6), (3,3), (3,4), (3,5), (3,6), (4,4), (4,5), (4,6), (5,5), (5,6), (6,6).
ATENÇÃO: Deve-se observar que não questão o enunciado não fala que os dados são distinguíveis, logo as repetições de grupos são desprezíveis. Essa consideração é feita por esta banca.
-
Ola gostaria de ver seu quadro colega:
-
Como temos dois dados de 6 jogados ao
mesmo tempo, temos um total de 36 (6x6) possibilidades de combinações, mas,
devemos considerar apenas pares que não são repetidos:
Ex.: {1,5} e {5,1} só consideraremos o
{1,5} e assim por diante.
Teremos 6 pares dos 36 que não vão
repetir: {1,1};{2,2};{3,3};{4,4};{5,5} e {6,6}
Então, 36 – 6 = 30. Desses 30 restantes,
15 não repetiram, logo: 15 + 6 =21
Logo, teremos um espaço amostral de 21
possibilidades (sem repetição).
Abaixo, vemos as possibilidades de que a
soma dos resultados seja um número maior que 5 e menor que 10 (dentro das 21
possibilidades sem repetição):
{1,5};{1,6};{2,4};{2,5};{2,6};{3,3};{3,4};{3,5};{3,6};{4,4};{4,5},
assim temos 11 possibilidades.
Logo, a probabilidade será: 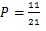
Letra E.
-
Alguém poderia responder a questão? Estou boiando nos comentários anteriores...
-
Não sei o modo de resolver, mas analisando cada caso:
Soma 1: Não tem combinação correspondente
Soma 2: (1,1)
Soma 3: (1,2)
Soma 4: (1,3) (2,2)
Soma 5: (1,4) (2,3)
Soma 6: (1,5) (2,4) (3,3)
Soma 7: (1,6) (2,5) (3,4)
Soma 8: (2,6) (3,5) (4,4)
Soma 9: (3,6) (4,5)
Soma 10: (4,6) (5,5)
Soma 11: (5,6)
Soma 12: (6,6)
Os em negrito são os que estão entre 5 e 10 (6,7,8,9), são 11. E no total são 21 possibilidades. Logo 11/21. Mas como resolver sem ver todas a possibilidades eu não consegui...
-
Encontrei 11 possibilidades possíveis da mesma forma que o colega Thiago achou. Marquei logo a letra E. No entanto, acredito que tenha uma forma de calcular usando os dados da questão. Quem souber, por favor, nos diga porque resolver da forma lógica leva muito tempo e não queremos perder tempo na prova.
-
Pra mim a banca errou. Já fiz outras questões IDENTICAS de outras bancas e acertei. Apliquei a mesma "fórmula" nessa questão e falhou. Basta contar quantas vezes o resultado é possível (soma maior que 5 e menor que 10) e dividir por 36 (numero de lançamentos possiveis). Deu 5/9. A proposito: http://www.ufjf.br/cursinho/files/2012/05/Aula-6.pdf questão 6, letra d.
-
Possibilidades:
1 e 5
1 e 6
2 e 4
2 e 5
2 e 6
3 e 6
3 e 4
3 e 5
3 e6
4 e 5
6 e 1
Total: 11 possibilidades. Pode sair 1 e 5 ou 5 e 1, então conta-se 2 vezes= 21. Não sei se está correto.