-
15 possuem somente doutorado e não são professores universitários.10 possuem doutorado e mestrado e não são professores universitários.20 possuem somente mestrado e não são professores universitários.45 juízes possuem o título de doutor ou de mestre mas não são professores universitários.
-
O amigo acima errou, as contas mas acertou a questão.
35 Juizes possuem o titulo de doutor ou de mestre mas não são professores universitários.
-
45 desses juízes possuem o título de doutor ou de mestre mas não são professores universitários.
-
acompanhe o raciocínio Julio:
20 "somente" mestre e ñ professor + 15 "somente" doutor e ñ professor + 10 mestre e doutor ao mesmo tempo e ñ professor = 45
-
Somente mestre: 20
Somente Doutor: 15
Doutor e mestre:10
Total: 20 + 15+ 10= 45...........menor que 50. Resposta: Certo
-
Resolvendo por Diagrama de Venn, temos:
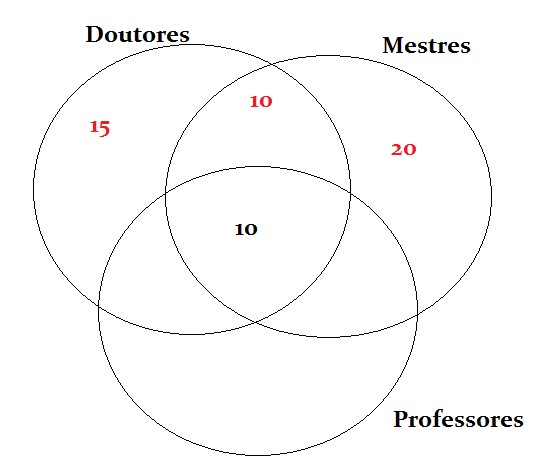
Somando: 15 + 10 + 20 = 45
Resposta: Certo.
-
A banca só tenta confundir. Quando diz que juízes possuem SOMENTE título de uma coisa, obviamente que não tem de outras:
Somente mestre: 20 + Somente doutor: 15 + Mestre e doutor e não professor: 10 = 45 juízes
45 < 50 , Portanto, gabarito está Certo.
-
Tem muita gente errando nos cálculos e nos comentários se a questão mudasse de forma iriam todos errar o único que falou certo é juliothecesar sobrenome
-
GAB: E. 35 é a resposta, pois a interseção dos 3 é 10, subtraindo de cada um, vai dar no doutorado 15, doutorado e mestrado 0, e mestrado 20.
-
GAB. C
Doutores Mestres
P.universitário 40 (10) 50
____________________________________________
ñ P. universitário 15 (10) 20 =45
-
Gabarito: CERTO.
Eu fiz o diagrama, mas como aqui não é possível postar imagem colocarei os resultados de cada parte do conjunto.
Total de Mestre: 50.
Somente Mestre: 20
Total professor universitário: 50
Somente professor universitário: 5
Total Doutor: 40
Somente Doutor: 15
Interseção Mestre e professor universitário: 20
Interseção professor universitário e Doutor: 15
Interseção Doutor e Mestre: 0 (Já que retira a interseção dos três)
Interseção dos três: 10
Como o conjunto que tem professores universitários não conta, então o total fica 35, como 35 é menor que 50, o gabarito é certo mesmo.
Bons estudos!
-
Maycon Leite o gabarito é CERTO!!
Como vc mesmo explicou o total fica 35, como 35 é menor que 50.
E a questão pergunta se "Menos de 50 desses juízes possuem o título de doutor ou de mestre, mas não são professores universitários."
-
Isso mesmo, Everton! Eu errei na hora de digitar o gabarito, mas a explicação está certinha como vc mesmo salientou. Obrigado por avisar!
-
Essa questão tem tanta informação que em um primeiro momento chega a dar medo na hora da resolução, mas lendo o que a questão pede fica fácil.
APF.
-
35 ou 45? Confesso que fiz de cabeça e respondi rapidamente. Contei 45.
-
GAB. C
Doutores Mestres
P.universitário 40 (10) 50
____________________________________________
ñ P. universitário 15 (10) 20 =45
-
35 juízes possuem o título de DOUTOR ou de MESTRE e não são professores. (15 são doutores e 20 mestres). Dá pra fazer desenhando o diagrama de Venn com três conjuntos: doutores, mestres e professores.
-
TEM OS QUE SÃO APENAS DOUTORES: 15
OS QUE SÃO APENAS MESTRES: 20
E NÃO ESQUEÇAM DOS QUE SÃO DOUTORES E MESTRES AO MESMO TEMPO MAS SEM SER PROFESSORES UNIVERSITÁRIOS: 10
TUDO ISSO DÁ 45.
-
Encontrei 45 usando 4 diagramas.
-
Adversativa sem vírgula me causa uma tristeza profunda.
-
45 são mestres ou doutores, mas não são prof universitários.
-
o raciocinio do Maycon Leite esta super correto !!!!!!! o total fica 35!!!!!!!!!!