-
Só consegui encontrar a letra D como resposta. B = 118 e C = 79
Alguém que tenha conseguido encontrar a letra C como resposta poderia explicar a resolução?
-
acabei de responder a questão e encontrei a letra "C" Concurseiros L3
é assim, fica mais fácil usando diagramas, mas vamos lá:
temos na sala 400 pessoas.
ai os dados são os seguintes, 339 tem a nacionalidade "A", 6 tem as três A;B;C, 80 têm as cidadanias A e B, somente 21 têm as cidadanias B e C, e somente 41 têm as cidadanias C e A.
Sabe-se, também, que o número de passageiros com apenas a cidadania B é igual ao número de passageiros com apenas a cidadania C. (essa informação será muito importante em breve).
sendo assim vc soma os dados cidadania "A" (339) esquece as outras que tenha "A" pois já estão inseridas nesse valor de 339 e soma as cidadanias "B(união)"C" então temos: 339+21=360 esse valor refere-se à quantidade de pessoas com nacionalidades "A" e com mais de uma. para saber só B ou C tem,os que subtrair do total na sala que são 400. 400-360 =40. lembra da informação que disse que era importante? pois bem diz que B é igual a C, correto?
então basta dividir 40 que foi o que sobrou do total por 2, assim temos valores idênticos para ambas as nacionalidades.
sendo que apenas nacionalidade "B" é 20 e "C" também basta somar agora dodos os valores que tiverem C depois B.
soma de "B":
Seis passageiros têm exatamente as três cidadanias. 80 têm as cidadanias A e B, s 21 têm as cidadanias B e C,
20+80+21+6 = 127
soma de "C"
41 têm as cidadanias C e A.
21 têm as cidadanias B e C
6 pessoas tem A; B e C
20+41+21+6 = 88
resposta "c" 127 e 88 respectivamente.
-
Anderson, concordo com sua resolução, porém gostaria de saber se considerou o fato de que enunciado diz: "21 passageiros têm as cidadanias B e C". Isso quer dizer que estão 15 passageiros contidos na intersecção de B e C e 6 estão contidos na intersecção de A, B e C, totalizando os 21.
Isso alteraria o resultado da questão para a alternativa (D).
O que acham?
-
Eu cheguei na letra D, fiz e refiz a questão e realmente o 6 engloba os 3 então B e C só podem ter 15 pois soma-se com o 6 e dá os 21, não consigo enxergar de outra forma, pra mim o gabarito está equivocado.
-
Bom pessoal esse exercício é razoavelmente fácil, é mais interpretação..vamos lá..
Primeiro temos que achar o x de B e C
A intersecção de B e C é 21 e A equivale a 339.
339+21+2x=400
360+2x=400
2x=400-360
x=20
Agora soma as intersecções:
B = 80+6+21+20 = 127
C= 41+6+21+20 = 88
Espero ter ajudado.
-
como os 6 que possuem as 3 nacionalidades estao inclusos nos 339 de a, ao somar a com b uniao c, deve-se somar somente 15 aos 339, pois se somarmos 21 aos 339 estariamos contando duas vezes os 6 que possuem as tres nacionalidades
-
como os 6 que possuem as 3 nacionalidades estao inclusos nos 339 de a, ao somar a com b uniao c, deve-se somar somente 15 aos 339, pois se somarmos 21 aos 339 estariamos contando duas vezes os 6 que possuem as tres nacionalidades
-
Existe uma pegadinha na questão. A palavara "exatamente". Isso quer dizer as interseções AB, AC e BC não se excluem os 6 passageiros das 3 nacionalidades.
-
a questão deu trabalho mais eu consegui responder.
-
Bom, fiz os conjuntos e fui descobrindo quem era cada um pelos dados fornecidos na questão.
1) Descobrindo quem é A
A= 339
A= APENAS A + (AB) + (AC) + (ABC)
339 = APENAS A + 80 + 41 + 6
339 = APENAS A + 127
APENAS A = 339 - 127
APENAS A = 212
2) Descobrindo B e C (sabendo-se que os valores de B e C são iguais, x será dividido por 2)
UNIVERSO = 400
X = 400 - APENAS A + AB + AC + ABC + BC
X = 400 - 212 + 80 + 41 + 6 + 21
X = 40
X/2 = 20
B = 20 e C = 20
2) Descobrindo universo de B
B = APENAS B + AB + BC + ABC
B = 20 + 80 + 6 + 21
B = 127
3) Descobrindo o universo de C
C = APENAS C + AC+ BC + ABC
C = 20 + 41 + 21 + 6
C = 88
-
Na minha resposta só da C meu diagrama está assim: a intersecção dos três coloque o 6,na intersecção de A e B coloquei 74 por que ele disse que era 80 como já tem 6,na interseção de B e C coloquei 15 ele disse que são 21 já tem 6 e na intersecção de A com C coloquei 35 ele diz que é 41 já tem 6,onde fica só B e só C coloquei x no A fiquei confuso com a informação dos 339 primeiro eu subtrai 339 do que tinha e depois eu coloquei os 339 mas nenhum deu certo e como posso somar 339 com 21 se nos 339 já estão os 6 não seria fazer 339+15+x+x=400?Dúvida.
-
tbm só consegui achar a letra D como resposta.... E não entendi as explicações
-
Para mim, essa questão se tornou confusa por afirmar na primeira frase: "Na sala de embarque de um aeroporto, há, no total, 400 passageiros com as cidadanias A, B OU C, APENAS" ....Me fez pensar que 400 seria o total de pessoas portadoras apenas de A, ou só B, ou só C....Aí as contas não fecharam rsss...
-
O Cícero Maciel esclareceu muito bem, a questão aqui não é que não se entenda o diagrama é que não pegamos o enunciado corretamente, a palavra exatamente para os passageiros de duas cidadanias acaba com a discussão. Obrigada Cícero.
-
Temos o seguinte, fornecido pelo próprio enunciado:
TOTAL: 400 pessoas.
COM A, B E C: 6
COM A E B: 80
COM B E C: 21
COM C E A: 41
COM, PELO MENOS, A: 339
Para solução precisaremos saber exatamente quantos possuem apenas a cidadania A. Então:
339(possuem pelo menos A) - 41(possuem A e C) - 80(Possuem A e B) - 6(Possuem as três) = 212
COM SOMENTE A: 212
Agora precisamos descobrir quantos possuem apenas B ou apenas C. A quantidade é a mesma para os dois, vide o enunciado.
Então:
400 (todos os presentes) -6 (Possuem TODAS as cidadanias) -212 (possuem apenas A) -80 (Possuem B e A) -21 (Possuem B e C) -41 (Possuem C e A) = 40
Temos então que 40 pessoas possuem apenas B OU apenas C. Como as quantidades são iguais, dividiremos por dois. Logo:
COM SOMENTE B: 20
COM SOMENTE C: 20
Ainda não é a resposta da questão. A questão pede o número de passageiros que possuem, PELO MENOS, B e o número de passageiros que possuem, PELO MENOS, C
Logo:
POSSUEM PELO MENOS B: 20 + 80 + 21 + 6 = 127
POSSUEM PELO MENOS C: 20 + 41 + 21 + 6 = 88
Então resposta C) 127 e 88
Espero ter ajudado. Abraço!
-
A chave da questão é o exatamente como disse o colega.... Se a questão fala extamente duas nacionalidades, não tem como ter 3 nacionalidades, logo, o 6 não é subtraido das intercseções.... Faz assim que dá certo.
VQV!
-
Pessoal, a questão é facilmente resolvida se utilizar conjuntos geométricos, faça 3 círculos interconectados chame-os de A, B e C, leia o enunciado de vagar e vá preenchendo as conexões, ao final do enunciado irá perceber os valores de forma visual lógica. O desenho é semelhante a este:
http://static.commentcamarche.net/www.commentcamarche.net/faq/images/tUpiA3wt-venn-diagrams-s-.png
porém, basta substituir todos estes nomes e preencher com valores.
-
Questão deveria ser anulada. O gabarito é letra D. A intersecção dos conjuntos A, B e C não é excludente.
Para encontrar as intersecções entre 2 conjuntos é pegar o valor dado e diminuir de 6.
Meu diagrama de veen ficou assim :
Somente A = 224 ( 339 - 74 - 35 - 6 );
Somente B = 23;
Somente C = 23;
ABC = 6;
AB = 74 ( 80-6 );
AC = 35 ( 41-6 );
BC = 15 ( 21-6 );
Se todo A é 339 e eu já tenho a intersecção BC =15, Somo todo A e BC -> 339+15 = 354;
Como o total é 400 pessoas e já encontramos 354...ainda temos 46 ( 400 - 354 ) para distribuir somente em B e somente em C.
No final do comando diz que B e C , "são respectivamente" , ou seja, são iguais...Pega o 46 e divide por 2 = 46/2 = 23;
Logo teremos 23 pessoas somente em B e 23 pessoas somente em C;
Agora somamos TODO B = 74+23+15+6 = 118;
Agora somamos TODO C = 35+23+15+6 = 79;
Espero ter ajudado e acredito que esse vídeo vai sanar as dúvidas. Simples e objetivo.
Fonte: Matemática em exercícios
Professor: Gui
https://www.youtube.com/watch?v=cDBSQldcJYY
-
Prezados colegas,
Resolvendo a questão cheguei no resultado B= 118 e C=79 (GABARITO D). Fui ver os comentários para poder verificar. Assim, não encontrando lógica nos que tentaram justificar o GABARITO C. Pois a justificativa que:
POSSUEM PELO MENOS B: 20+80+21+6 estará somando o da interseção 3 vezes. E a pergunta é " ...então é verdade que o número de passageiros com a cidadania B e o número de passageiros com a cidadania C são, respectivamente, ... " e NÃO PELOS MENOS !!!
Portanto a conclusão que chego que o GABARITO está incorreto, ou a questão mau formulada.
Grato.
-
No enunciado, devemos nos atentar para a palavra chave "somente", isso indica que não precisaremos subtrair os valores das cidadanias A e B, B e C, C e A da interseção A e B e C. Logo, fazendo o diagrama de Venn:
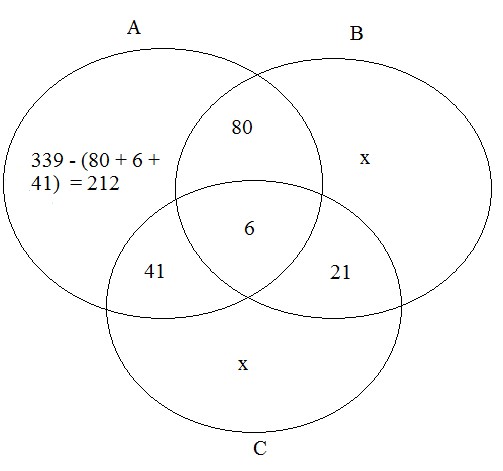
Para simplificar, sabemos que no valor de 339 já está incluso os valores de (A e B), (A e C) e (C, A e C). Assim, montando a equação abaixo:
2x = 400 - 360
x = 20
Logo, somando as interseções:
B = 90 + 6 + 21 + 20 = 127
C = 41 + 6 + 21 + 20 = 88
Resposta: Alternativa C.
-
Por causa da palavra "exatamente" (pegadinha) fica assim:
interseção A∩B∩C = 6
interseção A∩B= 6 + 80 = 86 não é 6 + 74
interseção B∩C= 6 + 21 = 27 não é 6 + 15
interseção A∩C= 6 + 41 = 47 não é 6 + 35
Somente A = 339 - 80 - 6 - 41 = 212
B + C = 400 - 212 - 80 - 41 - 21 - 6 = 40
Como B = C então temos:
Somente B = 20
Somente C = 20
Total de B = 20 + 80 + 6 + 21 = 127
Total de C = 20 + 41 + 6 + 21 = 88
Gabarito C
-
concordo com o amigo Paschoal acima
-
É... o Pulo do gato realmente está na expressão "Exatamente". O sacana do examinador nos da a intersecção de 6 apenas para nos confundir e plantar a maldade. Se ele tivesse colocado que 80 pessoas possuem a nacionalidade A e B, ficaria correto subtrair o 6. Mas ele disse expressamente que eles possuem exatamente as duas nacionalidades, ou seja, desnecessário subtrair o 6 em todas. Atenção redobrada agora!
-
Nossa, que peguinha lascado *-*
Apenas depois de ler os comentários conseguir entender a resposta correta!
-
Acho que a questão foi mal formulada porque não era para ser dito " que somente 80 têm as cidadanias A e B, somente 21 têm as cidadanias B e C, e somente 41 têm as cidadanias C e A."
Acho que o enunciado da questão deveria ser o seguinte: " 80 têm somente as cidadanias A e B, 21 têm somente as cidadanias B e C e 41 têm somente as cidadanias C e A.
-
Fiz da maneira tradicional não deu certo chutei e acertei rsrs.. mas como disse o pessoal a pegadinha está no termo "exatamente".
-
Fui pego pelo "somente".
-
valeu Gustavo muito bom
-
Eu fiz assim:
ABC = 6
AB= 80
BC= 21
CA= 41
somente B = somente C
Somei todos com cidadania B = 107 . Somei todos com cidadania C = 68 . Em seguida diminui 107 - 68 = 39 . Sabendo que somente B = somente C a diferença dos valores deveria ser 39. O que exclui 3 opções me deixando apenas com a alternativa C e D . E a única alternativa certa é a C pq realizando a subtração dos valores dados com 107 e 68 respectivamente vamos obter o mesmo resultado nas duas, o valor 20 que são apenas B e apenas C.
-
Alternativa C. ( A MALDADE
ESTÁ NA PALAVRA SOMENTE)
-
Gente... Nunca reclamem das materias de direito ;)
Vamos focar mesmo é em RLM :D TAMBEM ERREI ... TIREI OS 6 DAS OUTRAS INTERSEÇÕES...> O QUE NESSA QUESTÃO NAO PRECISA :)
-
Estava fácil demais pra ser verdade!! rsrsrs
-
A minha maior dúvida está na primeira frase: "Na sala de embarque de um aeroporto, há, no total, 400 passageiros com as cidadanias A, B ou C, apenas". Por causa desse APENAS, EU FIZ 400-212= 188 (dividi 188 por 2, porque o enunciado diz que o número de passageiros apenas com a cidadania B é igual ao número de passageiros apenas com a cidadania C)... Dai errei a resposta. E continuo com dúvida na questão, por causa desse primeiro APENAS
-
questão fácil, apenas atentar para as palavras somente, pois quando há a palavra somente, não diminuímos da intersecção das três nacionalidades. Casa o exercício não de a palavra somente, deve-se diminuir com base das intersecções.
-
passageiros= 400
A=339
B=C
C=?
A+B+C=6
A+B=80
B+C=21
C+A=41
A=339-6-80-41=212
A+B=80-6=74
B+C=21-6=15
C+A=41-6=35
212+74+15+35=336
400-336=64
64 DIVIDIDO EM B e C=32 PARA CADA
B=32+74+6+15=127
C=32+35+6+15=88
-
Achei a resolução da Nathalia Pereira
a de mais fácil compreensão de todos nossos amigos até agora, pois ontem quando eu li, já estava com a mente cansada e não havia entendido nada. Acredito que a Amanda Lima usou de ironia - desculpe, mas vamos ser mais sérios aqui. O gabarito diz que a alternativa correta é a letra C.
-
Somente A = 212
Somente B= 20
Somente C= 20
A,B e C=6
A e C= 41
B e C=21
A e B= 80
Total de B= 127
Total de C = 88
Bons estudos.
-
Gente, isso é diagrama lógico, é simples... Façam 3 círculos (A, B e C) com intersecções entre eles, inclusive com uma intersecção que pegue os 3 círculos. Daí basta ir colocando os números de acordo com o enunciado, por exemplo, na intersecção tripla coloquem 6, que é a quantidade de passageiros com as 3 cidadanias. Só não esquecer de somar todos os números que estão dentro do círculo A quando ele diz que na sala há exatamente 339 passageiros com a cidadania A, ou seja, para achar quem tem apenas A soma-se 80 + 6 + 41 = 127 e subtrai de 339 = 212, portanto 212 passageiros tem APENAS a cidadania A... daí o resto é fácil, pra saber que somente B e somente C é 20, em cada, é só somar os números que já estão nos círculos... 212+80+41+6+21=360, ou seja, faltam 40, 40/2 = 20. Pronto, basta somar TODOS os números que estão em B e TODOS que estão no círculo C... não sei se deu pra entender...rsrsrsrsrs
-
Fiz da seguinte forma:
Encontrei o somente A
80 + 6 + 41 = 127
339 - 127 = 212 somente A
Agora somando B
80 + 6 + 21 = 107
Agora somando C
21 + 41 + 6 = 68
Sabendo que somente B é igual a somente C fiz por eliminação das questões possíveis:
a) 142 e 97
142 - 107 = 35
97 - 68 = 29
Alternativa A errada, pois somente B ficaria 35 e somente C ficaria 29.
b) 139 e 102.
139 - 107 = 32
102 - 68 = 39
Alternativa errada, pois somente B ficaria 32 e somente C ficaria 39.
c) 127 e 88.
127 - 107 = 20
88 - 68 = 20
Resposta correta, alternativa C, pois somente B e somente C são iguais, neste caso 20.
-
AHHHHHHHHHHHHHHHHHHHHHHHHHHHHH MOLEQUE.... DEMOREI MAIS CONSEGUI!
-
Errei pelo fato da compreensão do enunciado, quando ele diz: "sabe-se que somente 80 têm as cidadanias A e B". Acho que de forma mais correta seria: "sabe-se que 80 têm SOMENTE as cidadanias A e B". Ai ficaria dentro do que a questão pede. Fogo, enunciados ruins acabam atrapalhando =/
-
Flor Concurseira, repare que antes de a questão trazer "sabe-se que somente 80 têm as cidadanias A e B", ela traz "Em se tratando de passageiros com exatamente duas cidadanias...". Isso equivale ao que você disse: "sabe-se que 80 têm SOMENTE as cidadanias A e B". Espero tê-la ajudado.
-
Hahaha aajudou, colega Thiago. Cada dia um novo aprendizado. Obgggggg.
-
Gustavo Toledo, melhor comentário! ;)
-
AFF. Já vi perguntas dessa e quando se fala assim: " ...há, no total, 400 passageiros com as cidadanias A, B ou C, apenas... "
Esse APENAS no total me fez considerar que somente A + somente B + somente C = 400, e não o total de passageiros. Deu a entender que 400 seria o número de passageiros com somente UMA cidadania... Se tirasse esse APENAS do enunciado daria para entender que há 400 passageiros com as cidadanias A, B, e C, independentemente de única, dupla ou tripla cidadania. Esse APENAS no final me ferrou.
-
Vocês falaram do "somente", mas na minha opinião a questão não é essa. É uma questão de semântica...
"sabe-se que somente 80 têm as cidadanias A e B" é diferente de "sabe-se que 80 têm somente as cidadanias A e B" Neste caso, aí sim poderíamos considerar que não precisaria subtrair 6. No entando, com a primeira frase não...
O fato de não subtrair está em: "Em se tratando de passageiros com apenas duas cidadanias"
-
Na bolota do B tem (74 + 6 + 15) = 95
Na bolota do C tem (35 + 6 + 15) = 56
95 - 56 = 39
Dai fui subtraindo os números das alternativas até chegar na letra C, que é o (127 - 95 = 32) APENAS COM A CIDADANIA B
(88 - 56 = 32) APENAS COM A CIDADANIA C
-
Faço das palavras do colega Luciano Lima, as minhas.
Questão deveria ser anulada, a palavra "exatamente" não faz referência a exclusão da subtração. O gabarito é letra D.
A intersecção dos conjuntos A, B e C não é excludente.
Para encontrar as intersecções entre 2 conjuntos é pegar o valor dado e diminuir de 6.
Meu diagrama assim :
Somente A = 224 ( 339 - 74 - 35 - 6 );
Somente B = 23;
Somente C = 23;
ABC = 6;
AB = 74 ( 80-6 );
AC = 35 ( 41-6 );
BC = 15 ( 21-6 );
Se todo A é 339 e eu já tenho a intersecção BC =15, Somo todo A e BC -> 339+15 = 354;
Como o total é 400 pessoas e já encontramos 354...ainda temos 46 ( 400 - 354 ) para distribuir somente em B e somente em C.
No final do comando diz que B e C , "são respectivamente" , ou seja, são iguais...Pega o 46 e divide por 2 = 46/2 = 23;
Logo teremos 23 pessoas somente em B e 23 pessoas somente em C;
Agora somamos TODO B = 74+23+15+6 = 118;
Agora somamos TODO C = 35+23+15+6 = 79;
-
Temos o seguinte, fornecido pelo próprio enunciado:
TOTAL: 400 pessoas.
COM A, B E C: 6
COM A E B: 80
COM B E C: 21
COM C E A: 41
COM, PELO MENOS, A: 339
Para solução precisaremos saber exatamente quantos possuem apenas a cidadania A. Então:
339(possuem pelo menos A) - 41(possuem A e C) - 80(Possuem A e B) - 6(Possuem as três) = 212
COM SOMENTE A: 212
Agora precisamos descobrir quantos possuem apenas B ou apenas C. A quantidade é a mesma para os dois, vide o enunciado.
Então:
400 (todos os presentes) -6 (Possuem TODAS as cidadanias) -212 (possuem apenas A) -80 (Possuem B e A) -21 (Possuem B e C) -41 (Possuem C e A) = 40
Temos então que 40 pessoas possuem apenas B OU apenas C. Como as quantidades são iguais, dividiremos por dois. Logo:
COM SOMENTE B: 20
COM SOMENTE C: 20
Ainda não é a resposta da questão. A questão pede o número de passageiros que possuem, PELO MENOS, B e o número de passageiros que possuem, PELO MENOS, C
Logo:
POSSUEM PELO MENOS B: 20 + 80 + 21 + 6 = 127
POSSUEM PELO MENOS C: 20 + 41 + 21 + 6 = 88
Então resposta C) 127 e 88
Espero ter ajudado. Abraço!
-
✅ Alternativa C
Galera, fiz todo o procedimento passo a passo no Sketchtoy para facilitar ;) É só entrar no link:
http://sketchtoy.com/70150819