-
resolvi e achei a resposta com diagrama de venn, se alguém tiver dúvida eu explico.
-
Pedro se possível gostaria que explicasse. ;)
-
Desenhando fica mais fácil, mas vou tentar explicar aqui.
Bons estudos!
A 229
B 223
C 196
A e B 79
A e C 89
B e C 69
A e B e C 37
NENHUM 53
SOMENTE A 229 -
89 - 79 + 37 98
SOMENTE B 223 -
79 - 69 + 37 112
SOMENTE C 196 -
89 - 69 + 37 75
A)
275 pessoas utilizariam somente um dos produtos.
ERRADO
98 + 112 + 75 = 285
B)
112 pessoas utilizariam somente o produto C.
ERRADO
SOMENTE C = 75 (ver acima)
C)
225 pessoas utilizariam os produtos A e C, mas
não utilizariam o produto B. CERTO
229 + 196 – 79 – 69 – 89 + 37 = 225
D)
500 pessoas foram entrevistadas. ERRADO
PESSOAS ENTREVISTADAS = 229 +223 + 196 + 53 -
89 – 79 – 69 + 37 = 501
-
explique por favor
-
Vou tentar explicar. Essas questões que oferecem três opções tipo A,B e C . Maria, João e Andre, três opções de entrevistados sempre se resolve pelo digrama de Venn que são três conjuntos entrelaçados, a grande sacada deste tipo de problema é por onde se começa. A logica é começar pelo começo, mas esse não sempre pelos últimos dados do problema o centro da intersecção. Vamos primeiro preencher a intersecção dos A, B e C que é o 37 depois a interseccão do B e C que não é 69 pois quando coloque o intersecção do A, B e C eu já citei 37 dos 69 entrevistados então eu preencho a intersecção do B e C com 32. Agora partamos para intersecçaõ do A e B que também não é 89 pois eu tenho que descontar os 37 também dos que já estão na intersecção do A, B e C, Então eu desconto 37 de 89 ficam 52. Agora preenchemos a intesecçaõ do A e B que por sua vez também não é o valor original 79 e sim com desconto de 37 ficam 42, esse e o processo é bom que vc vá fazendo tudo nós conjuntos para não se perder.196 utilizaram o produto C que é 196 - a intersecção A, B e C 37- a intersecção C e A 52 - a intersecção C e B que é 32 em +196 - 37 - 52 - 32 = 75. Os seguintes e o mesmo processo 223 do produto B, é +223 - 37 - 42 - 32= 112. conjunto A e 229 - 37 - 42 - 52 = 98. percebe como os valor vão reduzindo de dentro para fora na medida que se vai preenchendo? pois é , a resposta certa é a somo de tudo que ta dento das intersecções de A e C sem pegar nenhum valor que esteja relacionado com o conjunto B pois a opção certa que é a C Diz :
-
Não Concordo com o Gabarito - Pra mim não há resposta.
Fiz através do Diagrama de Venn, mas não sei postar o "gráfico".
Utilização Exclusiva dos Produtos:
--------------------------------------------------------------------------------------
Produto A => Utilizado exclusivamente por 98 pessoas;
Produto B => Utilizado exclusivamente por 112 pessoas;
Obs: A Letra (B) está errada pois foi colocado como sendo a Letra (C) quem tem as 112 pessoas
Produto C => Utilizado exclusivamente por 75 pessoas;
-----------------------------------------------------------------------------------------
=> 52 pessoas Utilizam os produtos A e C
A Letra (C) está errada pois o exercício somou as partes
A (exclusiva) => 98 + C (exclusiva) => 75 + A e C (conjunta) => 52
Totalizando => 225
- Deveria ser utilizado somente as partes A e C (conjunta) => 52 pessoas
=> 32 pessoas Utilizam os produtos B e C
=> 42 pessoas Utilizam os produtos A e B.
=> 37 pessoas Utilizam os produtos A - B - C
=> 53 NÃO Utilizam NENHUM.
SOMA DAS PESSOAS ENTREVISTADAS = 501
Obs: A Letra (D) também está errada pois deveria constar 501 e não 500 pessoas.
Que DEUS nos abençoe !!!
-
Concordo com o Beto: esta pergunta deveria ter sido anulada, pois não há resposta correta. A opção C diz que "225 pessoas utilizariam os produtos A e C, mas não utilizariam o produto B", no entanto o correto seria afirmar que "225 pessoas as que utilizariam os produtos A OU C, mas não utilizariam o produto B".
Se somente 196 utilizariam o produto C, como é possível que 225 utilizariam A E C?
-
Paulo, não entendi porque você não desconta o "37" que é a interseção dos três, para achar cada valor individual...
-
Teria que ser: quantos fazem parte somente de A e somente de C, mas não fazem parte de B.
Do jeito que está, realmente dá a entender que é a interseção AC.
Montando o diagrama vc encontra A = 98 C = 75 e AC = 52. Excluindo o conjunto B, sobra 98+75+52 = 225.
-
Pergunta foi mal formulada. Para que o resultado seja a letra C, teria que ser: 225 pessoas utilizariam os produtos SOMENTE A ou B.
-
OI pedro, segui suas instruções e fui fazendo pelo diagrama. Foi ótimo. Pelo diagrama da perceber e entender a questão.
obrigada.
-
Alguém poderia explicar bem detalhado da maneira mais fácil de resolver, pq tenho dificuldades e demoro muito pra responder. Agradeço.
-
Resolve-se por conjuntos, OOO, começando pelos três valores juntos e assim por diante
-
Utiliza apenas A: 98 | Utiliza apenas B: 112 | Utiliza apenas C: 75 | Utiliza A e B: 42 | Utiliza A e C: 52 | Utiliza B e C: 32 | Utiliza A, B e C: 37 | Nenhum deles: 53, Logo: 98 + 52 + 75 = 225.
-
Resolver por conjuntos em uma prova pode demandar mais tempo... mas a sacada da questão é observar o enunciado, A e C: 52, A: 98, C: 75, logo: 98+52+75 = 225
-
Galera, encontrei este link aqui explicando a questão de maneria super fácil, para não errar mais ;)
file:///C:/Users/USER/Downloads/http---pleno.hostjet.com.br-img-site-recursos-068a57c185882430220a9511d7e31a6b.pdf
-
A e C é diferente de A ou C.
-
A ou C = 98 + 75 = 173
A e C = 98(produto A) + 75(produto C) + 52(consome A e C) = 225
-
Pelo diagrama de Venn, constatamos que:
98 utilizariam apenas o produto A, 112 utilizariam apenas o produto B, 75 apenas o produto C, 42 utilizariam os produtos A e B mas não utilizariam o produto C, 32 utilizariam os produtos B e C mas não utilizariam o produto A, 52 utilizariam os produtos A e C mas não utilizariam o produto B e 37 utilizariam os três produtos.
Com base nisso, podemos dizer que 98+52+75 = 225 pessoas utilizariam os produtos A OU C mas não utilizariam o produto B.
Como a alternativa apresenta o conectivo "e", a questão não apresenta resposta certa.
-
Vamos
resolver esta questão por diagrama de Venn, seguindo os dados do enunciado:
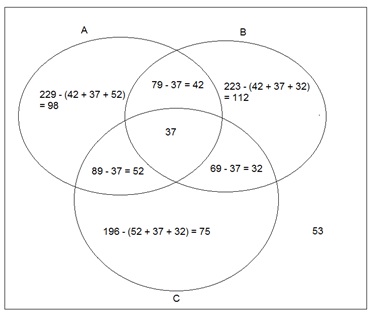
Logo,
de acordo com o diagrama de Venn, a resposta correta é a letra C, fazendo as
contas:
98 + 52 + 75 = 225
RESPOSTA: (C)
-
muitos números, mas temos todos os elementos para preencher o diagrama, então pra quem conhece o diagrama de venn, basta preenche-lo e depois ir eliminando as opções de respostas. resposta: ( c )
-
Realmente, uma questão como esta simplesmente é de deixar pasmo qualquer pessoa, pois não se pode ter uma questão deste tipo e que não se consegue chegar a uma resolução lógica, e ai, é nua a questão?
-
QUESTÃO TOP ! Vale a penas perder uns 5 min.
-
questâo errada !!!
.. produtos A e C, mas não utilizariam o produto B -> não posso somar 98 + 52 + 75 = 225 , isso seria A OU B !!!!
O texto é A e B !!!!!!!
-
A, B, C → A ^ B ^ C = 37
A, B → A ^ B = 79 - 37 = 42
A, C → A ^ C = 89 - 37 = 52
B, C → B ^ C = 69 - 37 = 32
A → 229 - 37 - 42 - 52 = 98
B → 223 - 37 - 42 - 32 = 112
C → 196 - 37 - 52 - 32 = 75
98+75+52=225
-
Entendi e acertei, não tem problema nenhum na questão. Porém, QUE QUESTÃO CANSATIVA!!! É pau fazer isso numa prova de concurso, ansiosa e já cansada. Os números e as letras ficam sambando no papel.
-
A) Somente um dos produtos: 98+112+75= 285....FALSO
B) 112 equivale ao produto B e não C. FALSO
C) 98+52+75= 225... VERDADE
D) O total equivale a 98+112+75+42+37+52+32= 501 pessoas... FALSO
#SEGUEOFLUXO
-
A) 275 pessoas utilizariam somente um dos produtos. (FALSO) 98+112+75= 285
B) 112 pessoas utilizariam somente o produto C. (FALSO) 112 equivale ao produto B.
C) 225 pessoas utilizariam os produtos A e C, mas não utilizariam o produto B = 98+52+75= 225 (VERDADE)
D) 500 pessoas foram entrevistadas (FALSO) 98+112+75+42+37+52+32+53= 501 pessoas.
-
IMAGEM RETIRADA DO COMENTÁRIO DO PROFESSOR.
TENTEI DESTACAR OS NÚMEROS COM CORES DIFERENTES PARA MELHOR VISUALIZAÇÃO, MAS NÃO O CONSEGUIR.
Autor: Vinícius Werneck, Matemático, MSc. e PhD Student em Geofísica., de Raciocínio Lógico
98 + 52 + 75 = 225
-
Não usam nenhum: 53
Usam os 3 produtos: 37
Usam ou B ou C: 69 - 37 = 32
Usam ou A ou C: 89 - 37= 52
Usam ou A ou B: 79 - 37 = 42
Usam somente A: 229 - (42+77+52) = 98
Usam somente B: 223 - (42+37+32) = 92
Usam somente C: 196 - (52+37+32) = 75
a) Pessoas que usam somente um dos produtos: 98+92+75 = 265
b) Usam somente o produto C: 75
c) Usam A ou C, mas não B: 98 + 75 + 52: 225
d) Pessoas entrevistadas: 53+37+32+52+42+95+92+75 = 478
-
A questão não resposta certa, na lógica os diagramas logicos se aquiparam a teoria de conjunto onde:
A e C significa A intercessão C, Sendo assim teria que dar como resposta 52
O correto seria se a letra C desta questão tivesse: A ou C
A ou C significa A união C, onde tal união é dada por:
A união C = (A-C) + (A^C) + (C-A) o que resultaria em 225
Faltou para a questão um bom recurso para a anulação da questão.
Prof. Talles Santiago.
-
Absurdo! Questão não possui gabarito correto! O próprio enunciado cita " 89 os produtos A e C", então todos as 225 PESSOAS devem obrigatoriamente usar os produtos A E C (CONJUNÇÃO). Admitindo que o gabarito é a letra C, admite-se o absurdo em se igualar "PRODUTOS A e C" com "PRODUTOS SOMENTE A + PRODUTOS SOMENTE C + PRODUTOS A e C".
-
O problema da questão está no "A e C", na minha opinião também não tem resposta. Com o diagrama de Venn o número de pessoas que utilizaria A e C menos B é 52. Quem só usa A ou só usa C não faz parte do conjunto "A e C". Não entendo quem comenta pra defender a banca, os próprios professores dizem que essa banca é campeã em deslizes e não admite o erro.
-
A questão foi trabalhosa, mas acertei. Em questão assim não é bom usar a lógica, pois certos números fazem diferença nos cálculos.
225 pessoas utilizariam os produtos A e C, mas não utilizariam o produto B. CERTO
Quando eles diz que 225 utilizariam o produto A e C, a banca considerou que é A U C, Pois ele não usa o termo Somente que no Caso seria A /\ B.
-
Pra quem segue defendendo que o conectivo e significa a soma de A e C (seja isoladamente ou pela interseção), o próprio enunciado, quando diz, por exemplo, que "89 os produtos A e C" considera apenas a interseção entre A e C, e não a somatória. Assim, o entendimento do enunciado e da resposta se contradizem. Não há gabarito para esta questão.