-
Regra do se.....então:
O valor lógico só será falso, se o primeiro for verdadeiro e o segundo for falso.
-
Essa catiane irrita, só põe gabarito...eu hein!
-
Galera essa foi uma das questões que mais tive dificuldades, achei uma resolução excelente mas não tem como coloca-la aqui por inteiro, então para quem quiser saber a resolução desse exercício.
http://beijonopapaienamamae.blogspot.com.br/2013/06/tecnico-tjam-2.html
Bons estudos!
-
Gente fala sério... Tem gente que coloca só o gabarito pq muitos não são assinantes e tem limite de gabarito por dia. Então pra essas pessoas só da pra saber qual o gabarito vendo os comentários. Por isso muita gente coloca só o gabarito, pra ajudar quem não tem acesso ilimitado,
-
*Supondo que ''André não é americano'' seja V
Se André não é americano, então Bruno é francês. (V)
V V (necessariamente Bruno é francês para dar V)
Se André é americano então Carlos não é inglês. (V)
F V OU F
Se Bruno não é francês então Carlos é inglês. (V)
F V OU F
*Supondo que ''André não é americano'' seja F
Se André não é americano, então Bruno é francês. (V) F V OU F
Se André é americano então Carlos não é inglês. (V)
V V
Se Bruno não é francês então Carlos é inglês. (V)
F (necessariamente F
Bruno é francês para dar V)
É obrigatório que Bruno seja francês.
gabarito - letra A
-
Reescrevendo
as sentenças através de símbolos lógicos:
I)
~AA→BF
II)
AA→~CI
III)
~BF→CI
Aplicando agora a tabela-verdade, encontraremos a resposta onde
as linhas das sentenças I, II e III sejam TODAS verdadeiras:
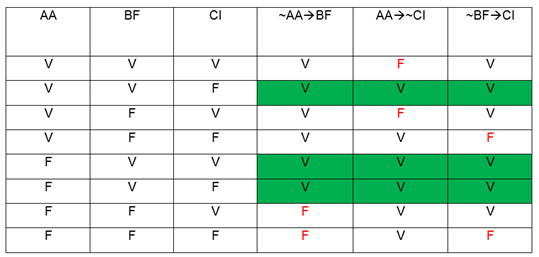
Temos então 3 linhas com os resultados desejados, notemos
que o valor lógico de AA e CI podem ser V ou F, logo não podemos decidir com
certeza se Carlos é ou não inglês e o mesmo acontece com André. Mas olhando a
tabela, veremos que BF é verdade nas 3 linhas, então obrigatoriamente Bruno tem
que ser Francês.
RESPOSTA: LETRA A.
-
CARACTERÍSTICA ÚNICA DA FGV!... A ÚNICA FORMA É APLICAR A TABELA VERDADE, OU SEJA, NO BRAÇO!!!
Aeua. Bfran. Cingl. ~Aeua.-->Bfran Aeua-->~Cingl ~Bfran-->~Cingl
v v v v f v
v V f V V V
v f v v f v
v f f v v f
f V v V V V
f V f V V V
f f v f v v
f f f f v f
A ÚNICA CERTEZA QUE TEMOS É QUE BRUNO É FRANCÊS, POIS - CONFORME A TABELA VERDADE - ELE É O ÚNICO ELEMENTO QUE NÃO SERÁ FALSO EM NENHUMA DAS PROPOSIÇÕES APRESENTADAS QUE NECESSARIAMENTE TÊM QUE SER VERDADEIRAS (lado direito da tabela)
GABARITO ''A''
-
Isso mesmo, Caroline. Quem não é assinante só pode resolver 10 questões por dia. E eu sou dessas pessoas. Acompanho os comentários por causa do gabarito também.
-
* comece a resolver de cima para baixo
Considere como verdadeiras as sentenças a seguir.
I. Se André não é americano, então Bruno é francês.
V --> V = V
II. Se André é americano então Carlos não é inglês
F --> ? = V ( no lugar da interrogação tanto faz ser verdadeiro ou falso, ambos vão me dar resultado verdadeiro)
III. Se Bruno não é francês então Carlos é inglês.
F --> ? = V ( no lugar da interrogação tanto faz ser verdadeiro ou falso, ambos vão me dar resultado verdadeiro)
Logo, tem-se obrigatoriamente que
letra A - Bruno é francês.
-
Eu resolvo essas questões com a Regra do Corte:
~A -> B . ~A -> B C -> B ~B -> B B (premissa: Bruno é Francês) não pode ser falsa, ela só pode ser verdadeira.
A -> ~C . C -> ~A ~B -> C
~B -> C . ~B -> C
-
Só consegui resolver pela tabela verdade !!
-
Se você não aprendeu a tabela verdade, não vai entender nenhum comentário. Essa tabela só se aprende com aula/vídeo ou livro e pratricando muito... no youtube tem.
Por dedução você pode até acertar, mas na hora da prova não vai ter essa frieza...
Procurem no youtube encadeamento lógico que isso vai te ajudar em questões parecidas a entender o que o Bruno fez
-
Eu fiz sem a tabela verdade, ficou um pouco extenso, mas deu certo, fiz assim:
Sabemos que para a sentença com o conectivo -> (se.. então) o valor lógico só será Falso quando V -> F.
Assim temos as proposições p, q e r:
p = André é americano
q = Bruno é francês
r = Carlos é inglês
Sentenças:
I. ~p -> q
II. p -> ~r
III. ~q -> r
Para resolver, como queremos que todas sejam Verdadeiras, peguei a primeira proposição de cada sentença e coloquei o valor lógico Verdadeiro, pois após o V só pode vir V, então:
1ª possibilidade: Digamos que ~p é Verdadeiro:
I. ~p = V -> q = V (valor lógico: V)
II. p = F -> ~r = V ou F (V)
III. ~q = F -> r = V ou F (V)
2ª possibilidade: Digamos que p é Verdadeiro:
I. ~p = F -> q = V (V)
II. p = V -> ~r = V (V)
III. ~q = F -> r = F (V)
3ª possibilidade: Digamos que ~q é Verdadeiro:
I. ~p = V -> q = F (F)
II. p = F -> ~r = F (V)
III .~q = V -> r = V (V)
Nesta possibilidade a primeira sentença ficou com valor lógico Falso, então não serve para resposta.(No meu raciocínio a primeira deu como Falsa, mas todas elas poderiam ter dado, depende da ordem com que você vai dando valores lógicos a cada proposição).
Analisando as possibilidades 1 e 2 a única proposição que mantém, com certeza, seu valor lógico 'V' é q = V, portanto, sendo a proposição q: "Bruno é francês", esta é a resposta da questão.
-
a opcao da resolucao por silogismo hipotetico seria uma boa. sai eliminando e no final fiquei com ~B -> B é que so os valores F -> V serviriam, logo Bruno é frances
-
Testando as três possibilidades do condicional o que funciono pra mim foi: [ F F ]
~A.A(?) condicional B.F(v) = V
A.A(?) condicional ~C.E(v) = V
~B.F(f) condicional C.E(f) = V
Deu verdadeiro na frente, NO CONDICIONAL, o proposição automaticamente é verdadeira.
*Gabarito* A
-
Podemos usar o método do “chute”. Assumindo que “André não é americano”:
- a frase I mostra que “Bruno é francês”;
- as frases II e III já estão verdadeiras;
- não podemos concluir nada sobre Carlos ser ou não inglês.
Já se assumirmos que “André é americano”:
- a frase I já está verdadeira;
- a frase II mostra que Carlos não é inglês;
- na frase III é preciso que “Bruno não é francês” seja F, pois “Carlos é inglês” é F.
Veja que, de qualquer forma, “Bruno é francês” é verdadeiro.
Resposta: A
-
Aprendi com um professor aqui do QC o seguinte método:
Encontrar equivalentes que formem uma cadeia lógica, em que o termo consequente de uma proposição seja o mesmo que o causador de outra proposição, logo, temos os dados da questão:
ñA -> B - essa vamos reescrever em ñB -> A
A -> ñC - nessa não mexeremos
ñB -> C - essa vamos reescrever em ñC -> B
Ficamos então com:
ñB -> A
A -> ñC
ñC -> B
ñB -> A -> ñC -> B
ou seja:
ñB -> B
Se Bruno não é Francês, Bruno é Francês
Então Bruno é Francês!
-
A forma mais rápida é fazendo pelo silogismo hipotético.
AA: André Americano
BF: Bruno Francês
CI: Carlos Inglês
I. Se André não é americano, então Bruno é francês = ~AA -> BF
II. Se André é americano então Carlos não é inglês = AA -> ~CI
III. Se Bruno não é francês então Carlos é inglês = ~BF -> CI
agora vamos fazer as contra-positivas e cortar os iguais
~AA -> BF = ~BF -> AA
AA -> ~CI = AA - > ~CI ( não faz contrapositiva dela, os dois AA se anulam virando ~BF->~CI)
~BF -> CI = ~CI -> BF (faz contrapositiva pra casar com o anterior, os dois ~CI anulam, terminando com ~BF->BF
~BR->BR
V F = F (não pode ser)
Então Bruno é Frances
-
Há o método de resolução chamado silogismo hipotético para o caso de só termos condicionais na questão, com o final de uma condicional coincidindo com o início de outra. Quando isso acontece, é possível cortar as premissas iguais e ter um argumento válido. Vamos para a questão:
I. Se André não é americano, então Bruno é francês (por equivalência lógica, vamos reescrever essa condicional: Se Bruno não é francês então André é americano - o voltar toda a proposição negando)
II. Se André é americano então Carlos não é inglês
III. Se Bruno não é francês então Carlos é inglês (por equivalência lógica, vamos reescrever essa condicional: Se Carlos não é inglês então Bruno é francês - o voltar toda a proposição negando)
Veja que é possível cortar as premissas André é americano e Carlos não é inglês (estão se repetindo nos pontos I, II e III), ficando apenas com a seguinte condicional: Se Bruno não é francês então Bruno é francês. É loucura se apenas lermos a condicional para um entendimento, mas em termos de lógica de argumentação isso é um argumento válido.
Acabei de comentar em uma questão semelhante - FGV usa muito esse método. E não há muitas funcionalidades de texto aqui no campo para comentários (queria riscar as premissas), mas espero ter ajudado alguma alma que estava perdida.
-
**Jeito mais rápido é testando alternativas!
A Bruno é francês.
---> se "Bruno é francês", não consigo saber se André é ou não americano e se Carlos é ou não inglês
B André é americano.
---> se "André é americano", então obrigatoriamente "Carlos não é inglês" e "Bruno não francês" --> alternativa C também estaria correta. Não pode!
C Bruno não é francês.
---> se "Bruno não é francês", então obrigatoriamente "Carlos é inglês" e "André é americano" --> alternativas B e D também estariam corretas. Não pode!
D Carlos é inglês.
---> se "Carlos é inglês", então obrigatoriamente "André não é americano" --> alternativa E também estaria correta. Não pode!
E André não é americano.
---> se "André não é americano", então obrigatoriamente "Bruno não é francês" --> alternativa C também estaria correta. Não pode!
-
Eu aprendi que numa questão como essa devemos responder de baixo para cima, mas não deu certo
-
Gabarito:A
Principais Regras:
- 50% das questões é para você verificar se o argumento é válido ou inválido e 50% é para você achar a conclusão. O método de RESOLUÇÃO é o mesmo.
- Às vezes, a banca coloca sinônimos, então atenção, pois 99,9% das questões que aparecerem sinônimos das palavras, você continuará resolvendo da mesma forma.
- Como identificar se o argumento é válido ou inválido? Passos: 1) Transformar as frases em siglas; 2)A conclusão vai ser SEMPRE FALSA e as premissas SEMPRE VERDADEIRAS; 3) Solucionar; 4) Se ao final, você resolver tudo sem encontrar erro, o argumento será inválido e se encontrar alguma divergência durante a resolução, será argumento válido.
Ex: A: Igor foi estudou e passou; B: Igor estudou; Conclusão: Igor passou;
1) Transformar as frases acima em siglas ou termos reduzidos - eu coloquei a primeira letra de cada termo, mas você pode fazer do jeito que for melhor, mas o intuito é reduzir as frases, logo ficará:
A (E ^ P); B (E); Conclusão (P)
2) As 2 primeiras sentenças serão as premissas que colocarei o valor final de verdadeiro e a conclusão de falsa. Logo, ficará:
A (E ^ P) = V; B (E) = V; Conclusão (P)= F
3) Solucionar
A única alternativa para solucionar é a premissa A. Logo ficará:
A (V ^ F) = V ?
No conectivo "e" quando se tem V ^ F, o final será Falso, logo ocorreu uma divergência.
4) Divergência, logo argumento válido.
- Já em relação as questões para achar a conclusão? O método descrito acima é aplicado, porém você deverá iniciar por sentenças simples, depois conectivo "e" e assim sucessivamente. Costumo dizer que é um pirâmide, a cada premissa resolvida, novas premissas serão abertas para você achar seu valor final. Geralmente existem diversas conclusões. CUIDADO: Exemplo: Premissa A: Carlos foi a festa; No momento que você identificar ao resolver que essa premissa é falsa, a conclusão trocará o valor semântico da frase, logo será "Carlos não foi a festa".
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
-
Pessoal, alguém resolveu essa questão pelo método do SILOGISMO HIPOTÉTICO? Se sim, podia compartilhar?
Obrigada =)
-
3 premissas
~A -> B
A -> ~C
~B -> C
Após realizar a equivalência lógica da primeira e da terceira premissas, consigo realizar o encadeamento lógico de todas elas, de modo a obter o seguinte:
~B -> A -> ~C -> B
Assim:
~B -> B
Para que a condicional resulte no valor lógico V, B necessariamente será verdadeira.
Logo, Bruno é francês.
-
Coloca no You Tube "Silogismo hipotético FGV", irá aparecer vários vídeos de Profs ensinando a responder esse tipo de questão.
-
Gabarito. A
I. Se André não é americano, então Bruno é francês.
~A então B
V > F = F
II. Se André é americano então Carlos não é inglês.
A então ~C
F > F = V
III. Se Bruno não é francês então Carlos é inglês.
~B então C
V > V = V
a) Bruno é francês (FALSO)
Pessoal nesse tipo de questão você adota a conclusão como FALSO. Se você achar alguma proposição FALSA, temos um argumento válido - resposta.
Conclusão FALSA e premissa FALSA = argumento VÁLIDO.
-
Fiz por equivalência lógica e deu perfeitamente certo.
-
a = André é americano
~a = André não é americano
b = Bruno é francês
~b = Bruno não é francês
c = Carlos é inglês
~c = Carlos não é inglês
Podemos resolver a questão rapidamente por Silogismo Hipotético:
~a->b
a->~c
~b->c
Utilizando a equivalência contrapositiva, podemos reescrever as premissas da seguinte maneira
~b->a (contrapositiva)
a->~c (mantém)
~c->b (contrapositiva)
O objetivo do silogismo é colocar o final de uma premissa idêntico ao inicio da próximo premissa, pois, assim, é possível cortar o final de uma com o início da outra.
~b->a (contrapositiva)
a->~c (mantém)
~c->b (contrapositiva)
Logo, chegamos ao resultado
~b->b
B pode receber o valor de V ou F e como a condicional só é falsa no caso de VF, obrigatoriamente:
~b = F
b = V
Logo, Bruno é francês.
-
Silogismo Hipotético FGV
https://www.youtube.com/watch?v=2KQJGMZC5ls
-
Alguém pode explicar por que faz a equivalência da primeira e da terceira e mantém a segunda? não dar certo fazer a primeira e a segunda ou a segunda e terceira?
-
GAB: LETRA A
Complementando!
Fonte: Prof. Eduardo Mocellin
Método da transitividade do condicional
Lembre-se que as afirmações são descritas por:
- ➧ Afirmação I: ~ a → b
- ➧ Afirmação II: a →~ c
- ➧ Afirmação III: ~ b → c
Ao concatenarmos a contrapositiva da afirmação II com a afirmação I, conclui-se c → b.
- Contrapositiva II: c →~ a
- Afirmação I: ~ a → b
- Conclusão I: c → b
Ao concatenarmos a afirmação III com a conclusão I, conclui-se ~ b → b.
- Afirmação III: ~ b → c
- Conclusão I: c → b
- Conclusão II: ~ b → b.
Como a conclusão ~ b → b é uma consequência verdadeira das afirmações do enunciado, temos que b é verdadeiro.
Logo, é correto concluir b, isto é, "Bruno é francês". O gabarito, portanto, é letra A.
===
Q439057
-
Essas questões tem necessariamente que fornecer um dado específico do que ocorreu, ou que não ocorreu, caso contrário o tempo da prova toda é desperdiçado na questão, uma vez que o valor lógico do "se..., então" tem três casos de dar verdade.
-
Gab. A
Consegui resolver usando as opções de respostas e supondo que fossem falsas. Deu certinho.
-
Questão que pode ser resolvida não só silogismo hipotético, mas também pelo método das hipóteses.
Silogismo hipotético: faz as devidas equivalências e chegará ao resultado.
ou
Método das hipóteses: Considera todas as premissas verdadeiras e testa as possibilidades de acordo com a tabela-verdade do se->então.
V->V
F->V
F->F
1º a; d; e
2º a
Veja que a alternativa que mais se repete é a letra A.
Logo, gabarito A.
Pra cima deles e não deixe o inimigo agir.
Método MPP
Abraço.