-
Para resolver esse exercício usei o método de invalidar a questão sendo assim temos o seguinte:
Argumento 1
P1: A (V) <-> B ( V) = V
P2: C (V) -> A (V) ^D ( V)= V
P3: ~B (F) ^D(V)= F
C: ~C (F) = F
Argumento 2
P1: A (V) ^B (V) = V
P2: C (V) v D (V) = V
P3 : B (V) -> D (V) = V
C: ~C: F
Logo os argumentos são inválidos pois não se pode ter premissas verdadeiras com conclusão falsa.
Espero ter ajudado!
-
Nao concordo com gabarito, nao entendi. O argumento I para minha é super válido.
Usando o método da conclusão verdadeira, colocando a premissa p3 como verdadeira, pois nela temos uma conjunção, temos:
p1: A(f)<--->B(f)
p2: C(f)---->A(f)^D(v)
p3: ~B(v)^D(v)
c: ~C(v)
Desta forma temos todas as premissas verdadeiras e a conclusão tb.
-
Argumento válido é quando tenho premissas verdadeiras e conclusão verdadeira OU quando tenho conclusão falsa E PELO MENOS UMA PREMISSA falsa. Por ser tratar de premissas o valor lógico delas deverão ser obrigatoriamente verdadeiro, sabendo disso vamos começar com P3 no ARGUMENTO 1 por ser uma conjunção porque na conjunção para ser verdadeiro é necessário que os valores lógicos sejam todos necessariamente verdadeiros e na bicondicional para ser verdadeiro é necessário que os valores lógicos sejam iguais.
(ARGUMENTO I)
P1: T <--> E = V
F <--> F = V
P2: (T ^ FP) --> TS = V
( F ^ V) --> V/F
F --> V/F = V
P3: ~E ^ FP = V
V ^ V = V
P4: ~TS = V/F (argumento inválido) Por existir UMA POSSIBILIDADE DE MINHA CONCLUSÃO SER "FALSA" E MINHAS PREMISSAS VERDADEIRAS CONCLUÍMOS QUE O ARGUMENTO É INVÁLIDO!
(ARGUMENTO II)
P1: GE ^ SA = V
V ^ V = V
P2: GT v CV = V
V/F v V = V
P3: SA --> GV = V
V --> V = V
C: ~GT = V/F (argumento inválido) Mesmo situação do argumento 1
-
muito bom caro matheus, eu não me havia atido à questão do português, essas conjunções são fo.. para complicar a vida da gente. valeu!
-
Galera consegui resolver,façam o seguinte no primeiro argumento usem O METODO DAS PREMISSAS VERDADEIRAS
Já no segundo usem o MÉTODO DAS CONCLUSÕES FALTAS,DEPOIS ME DIGAM ,HEHE
BOA SORTE
-
Galera, no gabarito oficial a resposta correta é a alternativa "c". No site do PCI concurso tem a prova e o gabarito. Ps. Murilo Cunha resolveu corretamente.
-
Pessoal, o Pedro Cardoso está correto, tanto que segue a resolução do argumento II:
p1: A^B ...... V ^ V ......(V)
p2: CvD ....... (V ou F) v V .......(V)
p3: B -->D ....... V --> V ...........(V)
c: ~C ....... V ou F
Logo esse argumento é indefinido e isso o leva a ser um argumento INVALIDO.
-
Olá, pessoal!
Essa questão não foi alterada pela Banca. O gabarito oficial indica alternativa como ERRADA. Conforme publicada no Edital de Gabarito no site da Banca.
Bons estudos!
Equipe Qconcursos.com
-
Argumento I
p1: Trabalho se e somente se estudo. T E = V T = F / E = F
p2: Terei sucesso, se trabalhar e for proativo. T ^ P -----> S = V S =V
p3: Não estudei, mas sou proativo. ~E ^ P = V ~ E =V / P = V
c: Logo, não terei sucesso. ( FALSO)
Argumento II
p1: Gosto de estudar e sou aventureiro. E ^ A =V E = V A =V
p2: Gosto de trabalhar ou de viajar. T V S = V T=?
p3: Se sou aventureiro, então gosto de viajar. A ----> S = V A =V S = V
c: Logo, não gosto de trabalhar.(????)
Um argumento será considerado Inválido quando as premissas são verdadeiras e a conclusão é falsa.
O argumento I é inválido
O argumento II não se pode afirmar nada sobre ele!
Observando as assertivas acima sabendo que temos que ter uma resposta certa, o ideal seria assinalarmos a letra b)
-
Pessoal vcs estão começando a resolver a questão pela ''conclusão'' é por isso que está havendo erro... Comecem a resolver pelas ''premissas'' e perceberão que tanto a ''conclusão'' do ARGUMENTO 1 quanto do ARGUMENTO 2 está indefinida, ou seja, não posso classificar como V ou F
-
mateus taliuli
VC É O MÁXIMO. sem vc eu não teria a aprendido como resolver esse tipo de questão! Obrigada!
-
Argumento nada mais é do que um conjunto de proposições (chamadas
premissas, que assumiremos como verdadeiras) associadas a uma conclusão. As
mesmas podem ser:
- válido, quando a conclusão é consequência
obrigatória das premissas;
- inválido, a verdade das premissas não é
suficiente para garantir a verdade da conclusão.
Geralmente a questão fornece informações (que são as premissas) que
aceitaremos como verdadeiras.
Se as premissas forem verdadeiras, a conclusão também será, logo temos
um argumento válido. Se não, o mesmo é
inválido.
Se o argumento apresentar os conectivos (proposições simples ou
compostas), podemos utilizar os conceitos das Estruturas Lógicas ou usar
Tabela-Verdade.
Estruturas Lógicas:
Reescrevendo os argumentos:
Argumento I)
p1: T ←→ E
p2: (T ^ P)→S
p3: ~E ^ P
c: ~S
Vamos começar por p3, consideraremos todas as premissas como
verdadeiras, valorando cada proposição de tal maneira que se tenha tal
resultado. Caso consigamos realmente ter todas as premissas e conclusão verdadeiras,
teremos um argumento válido, caso a conclusão de falsa, o argumento será
inválido.
Obs.: Escolhe-se sempre começar pela conjunção, pois a mesma só tem uma
possibilidade para que uma proposição seja verdadeira (V ^ V = V).
p3: V ^ V = V
p1: F←→F = V
p2: (F ^ V)→ (V ou F) = V
c: Se em p2 S for V então a conclusão será F e o argumento será
inválido, mas se em p2 S for F, a conclusão será V e o argumento será inválido.
Devido a isso, não podemos chegar a uma definição, sendo assim o argumento será inválido.
Utilizando o mesmo procedimento que fizemos para o argumento I), temos:
Argumento II)
p1: GE ^ A
p2: GT v GV
p3: A→GV
c: ~GT
Valorando:
p1: V ^ V = V
p3: V→V = V
p2: (V ou F) v V = V
c: Pelas mesmas razões explicadas para o argumento I, também se aplica
ao argumento II, logo o mesmo também é inválido.
Tabela-Verdade:
Agora, usarei a tabela-verdade para explorar o Argumento II:
p1: Gosto de estudar e sou aventureiro.
p2: Gosto de trabalhar ou de viajar.
p3: Se sou aventureiro, então gosto de viajar.
c: Logo, não gosto de trabalhar.
Contando as proposições que formam as premissas, temos:
Gosto de estudar = GE
Sou aventureiro = SA
Gosto de trabalhar = GT
Gosto de trabalhar = GV
Logo de cara já teremos que montar uma tabela com 16 linhas.
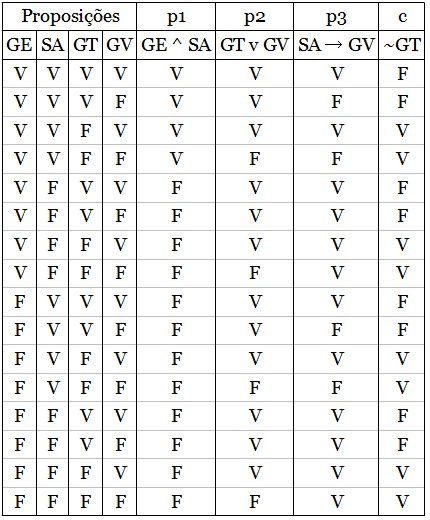
Assim, na tabela 1, devemos analisar. Devemos ter apenas
premissas verdadeiras, assim, só vão servir as linhas que p1, p2 e p3 tiverem
V, caso contrário, devemos riscar, logo, na tabela 2:
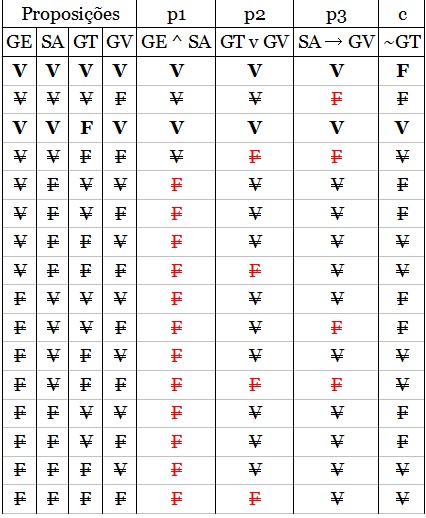
Apenas as linhas 1 e 3 trazem premissas verdadeiras, mas sempre
tendo premissas verdadeiras, teremos conclusões também
verdadeiras;
Como é o caso da premissa 1 na tabela, sendo assim, temos um argumento inválido.
Resposta: Alternativa B.
-
Que questãozinha do cão! aff..
-
Essa questão é inédia e vale a pena ser estudada.
Os dois argumentos podem ser Verdadeiros ou Falsos ( Não tem como saber)
Se não tem com saber ou o argumento for falso = Argumento Invalido
Letra B
-
Sobre o argumento I:
Com o método das premissas verdadeiras o argumento é válido, porém com o método da conclusão falsa o argumento é inválido.
E agora? rs.
-
Para ver se eu entendi: se eu coloco a conclusão falsa e as premissas forem verdadeiras, o argumento será inválido? Se as premissas forem falsas, então o argumento será válido?
Desde já agradeço!
-
PREMISSAS CONCLUSÃO ARGUMENTO
verdadeiras verdadeira válido verdadeiras falsa inválido pelo menos uma falsa verdadeira inválido pelo menos uma falsa falsa válido
Marjory Baxter...
-
Entendi dessa forma:
Argumento I
P¹: A <--> B / F <--> F = V
P²: (A ^ C) --> D / (~A v ~C) --> D / V --> V = V (V na frente, V atrás)
P³: ~B ^ C = V
LOGO: O argumento é inválido.
Argumento II
P¹: A ^ B / V ^ V = V
P²: C v D / F v V = V
P³: B --> D / V --> V = V
LOGO: O argumento é inválido.
Resposta: Letra B
-
Um argumento é valido se a conclusao é V sempre que todas as premissas forem V.
Então se vc encontrar um caso que a conclusao é V mesmo que alguma premissa seja F, o argumento é invalido. Eh o que acontece na questao.
"Condicao suficiente e necessária para a conclusao".
-
Errei porque achei que a conclusão no primeiro argumento não podendo ser falsa (já que P3 seria F), seria V. Mas neste caso é inválido porque a conclusão é F e um dos argumentos são falsos, ou porque a conclusão é falsa e P1 e P2 são V?
-
Galera, demorei mas entendi a questão.
__________________________________________________________________
Primeiramente não podemos começar dando valor falso para a conclusão, pois o método da conclusão falsa só usamos se não tiver outro meio de iniciar e neste caso os dois argumentos possuíam a conjunção. Dessa forma, se iniciarmos pela conclusão ficaremos sem saída no desenrolar da questão.
__________________________________________________________________
O bizú dessa questão é perceber que:
NO 1º ARGUMENTO, a P2 é verdadeira, mas contém uma proposição que pode ser verdadeira ou falsa e ela faz parte da conclusão também. "se trabalhar e for proativo, terei sucesso"
NO 2º ARGUMENTO, a P2 é verdadeira e a proposição que faz parte da conjunção também pode ser verdadeira ou falsa, note que ela também faz parte da conclusão. "gosto de trabalhar ou de viajar"
__________________________________________________________________
Se fosse uma proposição que não estivesse também na conclusão, não haveria problema algum de ela ser V ou F, mas nas circunstâncias em que o examinador elaborou a questão não há como afirmar se a proposição é V ou F. Como a proposição não é definida, o argumento não é válido.
Os dois argumentos apresentaram o mesmo padrão.
(Maldade do examinador)
-
Passivel de anulação... A 1 é válida. Por quê?
Método da conclusão verdadeira usando (Conjunção ou preposição simples) >> Temos a preposição simples na conclusão
Atribuir verdade para conclusão, e todas as suas premissas sendo verdadeiras = Argumento válido, do contrário, argumento invalido
Método da conclusão falsa usando (Disjunção, preposição simples ou condicional) >> Temos a preposição simples na concl...
Atribuir falso à conclusão, e pelo menos, uma delas for falso = Argumento válido, do contrário, argumento invalido.
-
Discordo do gabarito. O próprio professor Renato Oliveira de Raciocínio Lógico do QConcursos ensina-nos a resolvermos os argumentos começando da conclusão e considerando premissas e conclusão como verdadeiras, e resolvendo dessa forma os dois argumentos são válidos e a resposta seria A.
-
Depois de ler os comentário pude entender qual o erro do Argumento I, mas não consegui entender o Argumento II:
Argumento I
p1: Trabalho se e somente se estudo. (V) (Não se trabalha sem estudo.)
p2: Terei sucesso, se trabalhar e for proativo. (Essa é uma forma de se obter sucesso, porém a proposição não afirma ser a única)
p3: Não estudei, mas sou proativo. (V) (Sem muito o que acrescentar)
c: Logo, não terei sucesso. (Não se pode garantir que não se terá sucesso somente pelo fato de não ter estudado, pois o sucesso pode vir de outra forma que não pelo estudo, vez que a p2 não é taxativa)
-
É galera, o que torna a conclusão inválida é a impossibilidade de determinar se a afirmação é verdadeira ou não, mesmo que ambas satisfaçam a verdade.
-
A resposta correta é letra C, pois o argumento 1 é válido e o 2 é inválido. A maioria ta errando pq possivelmente começou a valorar a premissa errada. Tem que começar por uma conjunção ou proposição simples entre premissas... Ou faz pelo outro método, em que valora a conclusão como falsa e pressupõe-se que as premissas sejam verdadeiras. Por ambos os métodos O ARGUMENTO 1 É VÁLIDO.
-
Quem não entendeu que a B é a correta, é porque construiu erroneamente a P2, do Argumento I.
Argumento I.
P1. Terei sucesso, se trabalhar e for proativo.
Forma Errada: R --> ( P ^ S)
Forma Certa: ( P ^ S) --> R
Refaçam o Argumento I, usando o Método das Premissas Verdadeiras OU o Método da Conclusão Falsa e
verão que o Argumento de fato é Inválido.
Sobre o Argumento II, não resta dúvidas, ele é Inválido.
-
QUEREM GARANTIR, VÃO PRA TABELA VERDADE! NA TABELA O RESULTADO É GARANTIDO, SE TÁ CM DUVIDA VAI NA ULTIMA OPÇÃO,,
A TABELA TE GARANTE O EXATO RESULTADO SOBRE: VÁLIDO OU INVÁLIDO!
DEMORA, MAIS O RESULTADO NÃO TE DEIXA DUVIDA!
-
Questões de Concursos
11 de Novembro de 2014, às 17h13
Útil (3)
Olá, pessoal!
Essa questão não foi alterada pela Banca. O gabarito oficial indica alternativa como ERRADA. Conforme publicada no Edital de Gabarito no site da Banca.
Bons estudos!
Equipe Qconcursos.com
Reportar abuso
Como marcar "ERRADA" se é de multipla escolha??? Ta Serto!
-
Argumento I
P1: F <-->F = V ( será verdade quando os valores lógicos forem iguais)
(P2 : se trabalhar e for proativo então terei sucesso)
P2 : (F^V)--> V = F -->V =V ( no "se então" só será falsa quando a 1° for verdadeira e a segunda falsa ; é no conectivo "e" só será verdade quando ambas forem verdade)
P3: V^V=V ( só será verdade quando ambas forem verdade )
Conclusão: falsa
Argumento inválido
ARGUMENTO II
P1: V^V=V (será verdade quando ambos forem verdade )
P2 : V v V=V ( só será falsa quando ambas forem falsa )
P3: V-->V=V( só será falso quando a primeira for verdadeira e a segunda falso)
Conclusão: falso
Argumento inválido
-
GABARITO: LETRA B;
Precisamos saber se ambos os argumentos são válidos ou inválidos.
Um argumento é válido quando a conclusão é consequência obrigatória do conjunto de premissas;
Um argumento é inválido quando a verdade das premissas não é suficiente para garantir a verdade da conclusão.
Nesse tipo de questão, consideramos as premissas verdadeiras e, em seguida, analisamos a conclusão fornecida.
Vamos analisar os argumentos de maneira separada...
Argumento I:
Considerando as proposições simples:
T: trabalho;
E: estudo;
P: sou proativo;
S: terei sucesso
Inicialmente, vamos reescrever todas as premissas em uma linguagem proposicional:
P1: T ↔ E
P2: T ∧ P → S
P3: ~ E ∧ P
C: ~ S
Iniciaremos pela P3, uma vez que temos uma conjunção e a única forma de ela ser “V” é obtendo valores lógicos verdadeiros em ambas as proposições. Veja:
P3: ~ E (V) ∧ P (V) ---- (V)
Agora, vamos encontrar os valores lógicos da P1:
P1: T (F) ↔ E (F) ---- (V)
Como ~ E é “V”, E será “F”. Sendo assim, obrigatoriamente T será “F”, uma vez que precisamos obter premissas verdadeiras.
Analisando a P2:
P2: [T (F) ∧ P (V)] → S (V) ou (F)
[F]
Como o antecedente da condicional é “F”, não se pode definir o valor lógico do consequente, uma vez que independentemente desse valor lógico, a condicional será sempre verdadeira.
A conclusão afirma que “não terei sucesso”. Nada se pode concluir em relação a essa afirmação.
Sendo assim, temos um argumento inválido, uma vez que a verdade das premissas não é suficiente para garantir a verdade da conclusão.
Argumento II:
Considerando as proposições simples:
A: sou aventureiro;
E: estudo;
T: gosto de trabalhar;
V: gosto de viajar.
Inicialmente, vamos reescrever todas as premissas em uma linguagem proposicional:
P1: E ∧ A
P2: T ∨ V
P3: A → V
C: ~ T
Iniciaremos pela P1, uma vez que temos uma conjunção e a única forma de ela ser “V” é obtendo valores lógicos verdadeiros em ambas as proposições. Veja:
P1: E (V) ∧ A (V) ---- (V)
Agora, vamos encontrar os valores lógicos da P3:
P3: A (V) → V (V) ---- (V)
Como A é “V”, V também será “V”, uma vez que precisamos obter premissas verdadeiras.
Analisando a P2:
P2: T (V) ou (F) ∨ V (V)
Como a proposição V é “V”, não se pode definir o valor lógico da proposição T, uma vez que independentemente desse valor lógico, a disjunção será sempre verdadeira.
A conclusão afirma que “não gosto de trabalhar”. Nada se pode concluir em relação a essa afirmação.
Sendo assim, temos um argumento inválido, uma vez que a verdade das premissas não é suficiente para garantir a verdade da conclusão.
Conclusão: Ambos os argumentos são inválidos.
-
Gente o Gabarito é B
Esta é prova tipo BRANCA , questão n° 11
-
No caso não há como provar a validade do argumento, por isso o mesmo é inválido, correto?
-
Argumento I
Da P3, teremos que não estuda e é proativo.
Da P1, como estudo é falso, também trabalho tem que ser falso. Então não trabalha.
Da P2, Se trabalhar e for proativo, então terei sucesso.
Como trabalhar é falso, então trabalhar e for proativo será falso. Assim, poderá ter sucesso ou não, pois a condição suficiente é falsa. Então o argumento é inválido. Assim elimina alternativas A e C
Argumento II
Da P1, gosta de estudar e é aventureiro.
Da P3, como é aventureiro, então gosta de viajar realmente.
Da P2, como gosta de viajar e temos conectivo “ou”, pode ser que goste ou não de trabalhar, pois já é verdadeiro.
Assim o argumento é inválido.
Alternativa B
-
A afirmação p2 do Argumento 1 ("Terei sucesso, se trabalhar e for proativo") é, como alguns já apontaram, relativa. O fato de o antecedente da condicional ser falso não necessariamente significa que o consequente não pode ser obtido. Veja o exemplo abaixo:
"Se João pular no lago, então ficará molhado".
Considere que João não pulou no lago. É impossível que João tenha ficado molhado? Não, não é. Há várias outras formas de se molhar que não pulando num lago.
-
Errei ao começar a questão considerando a conclusão verdadeira e a partir disso analizando as premissas. Pois a conclusão sendo verdadeira ou falsa, é possível fazer com que todas as premissas sejam verdadeiras.
Para resolver esse tipo de questão , onde é fornecido todas as premissas e a conclusão, e se pegunta se o argumento é válido, o esquema é:
1- Esquematizar o argumento
2- Forçar a conclusão a ser FALSA
3- Verificar se é possível que as premissas sejam ,ainda assim, todas VERDADEIRAS. (Utilizando as relaçoes lógicas de tabela-verdade)
4- Se for possível, o argumento é inválido. Caso contrário, o argumento é válido.
-
Deixe ver se eu entendi... quando tiver:
Se ...
Se, então ...
A conclusão é uma Incerteza?
-
Eu aprendi MEMORIZAR SÓ O ARGUMENTO INVÁLIDO, o resto que for contrario é válido
apliquei o argumento inválido e deu certo, já estou estressada!kkk
é o que as bancas pedem então pronto!!!
gab c
-
PREMISSAS - CONCLUSÃO - ARGUMENTO
Verdadeiras - Verdadeira - Válido
Verdadeiras - Falsa - Inválido
Pelo menos uma falsa - Verdadeira - Inválido
Pelo menos uma falsa - Falsa - Válido
Obs: Só organizei melhor o esquema que o Thiago Pietsch tinha postado.