-
Para a resolução é preciso de conhecimento sobre Cálculo Diferencial e Integral.
A probabilidade de P(Y>=10) é igual à integral da densidade de probabilidade exponencial: (1/10)*exp(-(y/10)), com os limites de integração indo de 10 a infinito. Como a integral de uma função exponencial é a própria função exponencial cairemos (após aplicar os limites) na expressão de P(Y>=10)=exp(-1), cujo valor foi dado na questão. Assim P(Y>=10)=0,37.
Entretanto, temos que P(Y>=10) + P(Y<10) = 1, disso chegamos a P(Y<10)=0,67 e portanto P(Y<10) > P(Y>=10). Gabarito: Errado.
.
-
Dada a função acumulada da exponencial: F(y) = P(Y<= y) = 1 - exp(-y * lambda), onde neste exemplo lambda = 1/10, temos que:
P(Y>=10) = 1 - P(Y<10) = 1 - [1 - exp(-10/10)] = exp(-1) = 0,37
P(Y<=10) = 1- exp(-1) = 0,63
Portanto, P(Y>=10) < P(Y<=10).
Gabarito: Errado
-
Sendo sincero, mas a cespe colocar uma questão desta na prova prova de escrivão é muita sacanagem.
-
Concordo ilustre colega Jhonata SrSz... NUNCA irá utilizar isso na vida funcional...
-
A função acumulada da distribuição exponencial é:

Portanto,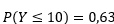 , de modo que
, de modo que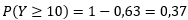 . Item ERRADO.
. Item ERRADO.
-
Meu amigo... e eu achando que sabia alguma coisa de Estatística.
-
É sério que o erro da questão não é o fato de o enunciado deixar uma hipótese impossível de acontecer ?
Qual seja: P(Y = 10 kg) > P(Y = 10 kg).
-
Negativo Delta Pragmático.
Thiago Rodrigues, resolveu de forma correta a questão. Se utiliza de integral e limites para resolver esta questão.
Porém, quem tiver um pouco de domínio matemático, e soubesse que a função exponencial em probabilidade é:
f(y) = lambda * exp(-y * lambda)
ou seja, temos uma exponencial elevando um número com sinal negativo.
Portanto, quanto maior o número, menor o valor da função.
Logo temos que P(Y<10) é maior que P(Y>10).
Sem cálculos.
-
Nem os professores do Q sabem o que comentar..
-
P(Y ≥ 10 kg) > P(Y < 10 kg).
QUESTÃO DISPENSA CÁLCULO, NÃO SE ILUDAM PELA PROBLEMÁTICA, O ENUNCIADO É MERA INTERPRETAÇÃO.
SE Y pode ser MAIOR OU IGUAL A 10 e POR OUTRO LADO, pode ser MENOR OU IGUAL A 10.
SUPÚNHAMOS QUE Y seja igual (já que pode ser maior ou igual) ----> P(Y=10)
A QUESTÃO FICARIA ASSIM:
P(Y=10) > P(Y=10)
O SINAL DE ">" ENTREGARIA A QUESTÃO, UMA VEZ QUE EM DISTRIBUIÇÕES CONTÍNUAS, A MÉDIA NO PONTO CORRESPONDE A ZERO, LOGO SERIAM IGUAIS. NÃO MAIORES.
-
Tarcísio, com todo respeito. Mas tem nada a ver isso aí. A questão quer saber sobre a probabilidade acumulada e não apenas de um ponto. Se o sinal fosse de "menos", com esse seu pensamento, teria errado a questão.
-
Cê é louco tio! To rindo de nervoso KKKKKK
-
f(x,y) = 1 - e^-yx = 1 - e ^ -0,1x10 = 1- 0,37 = 0,63 ( de 0 a 10 = 0,63 ) , logo a assertiva está errada
-
Resolvi sem cálculo algum, vamos a simples explicação:
A questão afirma que o estudo segue uma distribuição exponencial, logo, o gráfico possui assimetria positiva (a calda fica do lado direito, com isso a Média > Mediana > Moda). Temos a parte maior do gráfico a esquerda e considerando a média igual a 10, como afirma a questão, quanto mais a esquerda maior a probabilidade e quanto mais a direita menor a probabilidade, já que a calda fica a direita.
-
Caramba... kkkkkkkkkk
eu acertei achando que P era probabilidade...da fui na logica e acertei, mas nao recomendo...na prova deixaria em branco com certeza!
-
fácil P(Y ≥ 10 kg) > P(Y < 10 kg). tem o maior ou igual e menor ou igual, portanto os valores podem ser iguais e não maior
-
Melhor comentário : Tarcísio Vieira
Grata
-
A média é 10. então a probabilidade de valores menores que esse, ou valores maiores maiores que esse, É IGUAL. e não uma maior que a outra.
-
Misericórdia!
-
Questão cabulosa :( Nota de Corte da Prova foi 49 Pontos !! Cespe teve dó não .
-
Vamos por parte:
1)A distribuição exponencial é assimétrica. Logo P(Y>=10) é diferente de P(Y<10)
2)A função de distribuição acumulada é dada por:
f(x,y) = 1 - e^-λx
3) dados da questão:
E(Y)=10
P(Y) = P(Y<=y)
e^-1=0,37
4) achando o parâmetro lambda (λ):
E(Y)=1/λ
λ=1/10=0,1
5) Jogando os valores na função de distribuição acumulada:
F(y)=P(Y<10)
F(y) = 1 - e^-λx
F(y)=1 - e^-0,1*10
F(y)=1-e^-1
F(y)=1-0,37
F(y)=0,63
6) P(y<10)=0,63
p(y>=10)=1-0,63=037
então:
P(y>=10)<P(y<10)
A questão inverteu, questão errada
-
Estatística descritiva (análise exploratória de dados) ,
Medidas de Posição - Tendência Central (Media, Mediana e Moda) ?
-
GABARITO: Errado.
Sabemos que a média dessa variável é igual a 10 kg, portanto, o parâmetro λ corresponde ao inverso desse valor, isto é, 0,1. Porém, podemos resolver essa questão sem aplicar o cálculo de função distribuição acumulada F(X), como foi indiretamente sugerido.
Isso porque, ao se perguntar a probabilidade de obter um valor maior ou menor que a média, em uma exponencial, sabemos a resposta simplesmente pelo fato de ser uma distribuição assimétrica positiva. Uma distribuição assimétrica positiva tem a média maior que a mediana, desse modo, abaixo da média temos mais que 50% dos dados acumulados e consequentemente acima da média, temos uma probabilidade menor que a metade.
-
Cara, eu acho que nem estatístico ia resolver essa questão na hora da prova.
Surreal cobrar uma parada dessa ...
-
Rapaz, como é que se bota uma questão dessa sem dar a função exponencial ?
Eu acertei, mas porque desenhei o gráfico e vi que assertiva não fazia muito sentido, uma vez que os valores iniciais de uma função exponencial decrescente são mais altos, logo a área é maior...no entanto, foi sorte, pq isso pode nem sempre ocorrer, dependo do valor de x adotado.
-
Isso porque, ao se perguntar a probabilidade de obter um valor maior ou menor que a média, em uma exponencial, sabemos a resposta simplesmente pelo fato de ser uma distribuição assimétrica positiva. Uma distribuição assimétrica positiva tem a média maior que a mediana, desse modo, abaixo da média temos mais que 50% dos dados acumulados e consequentemente acima da média, temos uma probabilidade menor que a metade.
-
kkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
-
Sabemos que a média dessa variável é igual a 10 kg, portanto, o parâmetro λ corresponde ao inverso desse valor, isto é, 0,1. Porém, podemos resolver essa questão sem aplicar o cálculo de função distribuição acumulada F(X), como foi indiretamente sugerido. Isso porque, ao se perguntar a probabilidade de obter um valor maior ou menor que a média, em uma exponencial, sabemos a resposta simplesmente pelo fato de ser uma distribuição assimétrica positiva.Uma distribuição assimétrica positiva tem a média maior que a mediana, desse modo, abaixo da média temos mais que 50% dos dados acumulados e consequentemente acima da média,temos uma probabilidade menor que a metade.
fonte alfacon sou+4.0
-
Para quem não sabe calcular função exponencial e nem sabe fazer lim, realmente, questão fica muito difícil de ser resolvida.
-
Na exponencial
P(X>=média) é sempre igual a 37%
P(x<=média) é sempre igual a 63%
-
Distribuição exponencial --> F(x) = λ . eˆ( -λ.x)
Função Distribuição Acumulada --> F(y) = P(Y ≤ y) = 1 - eˆ( -λ.y)
Média --> E(x) = 1 / λ --> 10 = 1/ λ --> λ=0,1
Comando da questão -->
Calcularei
F(y) = P(Y≤y)
F(10)=P(Y≤10) = 1 - eˆ( -λ.10) =1 - eˆ(O,1x10) = 1 - . eˆ(-1)
= 1- 0,37
= 1 - 0,37 = 0,63
Ora se P(Y≤10) = 0,63, esse é maior que seu complemento com certeza
considerando que P(Y=10) é um numero bem próximo de 0
Gabarito Errado!
-
ERRADO
Resolução em 4min
https://www.youtube.com/watch?v=yqwB6uVoQrc
-
Fazendo a integral encontra os 0.63 que o R e J falou!
-
No enunciado ele diz: "variável aleatória Y é igual a 10kg".
Na pergunta ele diz: "P(Y ≥ 10 kg) > P(Y < 10 kg)."
Eu interpretei da seguinte maneira:
P(10 ≥ 10 kg) > P(10 < 10 kg), ou seja, se y é igual a 10kg ela não pode ser > e nem <, e muito menos 10 > 10, portanto a fórmula está errada.
Estou errado no raciocínio?
Sempre poderei fazer assim neste tipo de questão?
-
Mais uma vez mostra-se necessário o entendimento da estatística descritiva...
Como é sabido exponencial = assimétrica positiva
Assim, Média > mediana > moda
Desse modo, os dados acumulados até a média são ,no mínimo, maior que 50% (já que essa é maior que a mediana que particiona metade dos dados), o que nos leva a crer que a probabilidade de y ser maior que a média é menor que a dele ser menor que a média, isto é, P(y > 10) < (y < 10)
O entendimento da função acumulada de probabilidade ajuda muito nessa situação
-
Pessoal, a questão é completamente teórica, você entendendo como funciona uma distribuição contínua, mataria essa questão só de olhar....
-
A probabilidade de P(Y < 10 kg) é dada pela Função de Distribuição Exponêncial acumulada
Função de Distribuição Exponêncial acumulada
probabilidade da estar ABAIXO de determinado valor ( no caso da questão , estar abaixo de 10kg )
Fórmula:
F( x , lambda ) = 1- e-lambda. x
#1) Descobrindo o valor de lambda
Fórmula :
Média = 1/ lambda
Logo, 1/ lambda = 10
Lambda = 0,1
#2) Aplicando na Fórmuça
F( 10, 0,1 ) = 1 - e-0,1.10
F(10,01) = 1- e-1
F(10,01) = 1- 0,37 ( valor dado pelo enunciado )
F(10,01) = 0,63
Logo , a probalidade de se INFERIOR a 10 é ( 0,63) > e a probalidade de ser SUPERIOR A 10 é ( 0,37)
-
A questão DISPENSA CÁLCULOS. Apenas memorizem: em uma distribuição EXPONENCIAL a probabilidade de ser MENOR que a média é de 63% e a probabilidade de ser MAIOR que a média é de 37%. A cespe adora enfeitar questão para cobrar conceitos.
-
P(Y ≥ 10 kg) > P(Y < 10 kg).
(y=10). >. (Y=10)
0. >. 0. = no posto seria zero
(y>10). >. (Y<10)
37 >. 63. Errado
-
gab ERRADO
Para a galera que não entendeu, eu ilustrei no gráfico SEM PRECISAR FAZER CONTA, questão simples, mas que exigia uma análise.
Para responder bastava entender que Me>Mo>m
Segue o link: http://sketchtoy.com/69513148
AVANTE
-
No gráfico da exponencial:
- do 0 à média (1/lambda) = 63% da área abaixo do gráfico
- da média ao infinito = 37% da área abaixo do gráfico
Como o exercício deu que a média de Y é igual a 10, sabemos que Y<=10 é maior do que Y>=10
A questão afirma o contrário, por isso o gabarito é ERRADO
-
cade a bruna?
-
Essa questão em específico não precisa de cálculo.
Veja o gráfico
https://sketchtoy.com/69547792
-
Sendo sincero, se cair esse tipo de coisa na prova de estatística, é muito bom. É apenas a teoria de uma exponencial, deixarei aqui alguns conceitos que poderão ser úteis:
Na exponencial
- Média = E(x), que é igual a 1/lambda, que é igual ao Desvio Padrão. E(x) = 1/lambda = DP
- A frequência é simbolizado por lambda., normalmente, ocorrências/minuto.
- E(x) > Me(X) > Mo(x) - "média maior que a mediana maior que a moda" é a sequência de uma exponencial. Já em uma distribuição normal, todas são iguais.
- e-1 = 0,37, ou 37% que é o valor provável de uma ocorrência acontecer maior do que a média!
- ou seja, 0,63, ou 63% é o valor provável de uma ocorrência menor do que a média.
- A probabilidade de algo acontecer no mesmo valor da média é igual a zero, ou seja: P(x=K) = 0 (tanto na exponencial como na normal, já caiu em algumas provas)
Então no exemplo:
Se a média da variável aleatória Y é 10, o desvio padrão será 10 e a frequência (lambda) será 1/10.
P (Y> 10kg) = 0,37, ou 37% de um número acima da média de 10kgs
P (Y < 10kg) = 0,63 ou 63% de um número menor do que a média de 10kgs
ou seja: P (Y<10kg) é MAIOR que P(Y>10kg).
Gabarito = Errada.
-
Nessa questão a melhor coisa pra não haver dúvidas é colocar no gráfico, oq vem depois da média será calculado por e(exp -lambda*x) e oq vem antes da média é 1-e(exp -lambda*x), logo como a média u=1/lambda, lambda ficaria igual a 0,1, jogando na fórmula Y>=10= e(exp -lambda*x)= 0,37, logo, Y=<10=1-0,37=0,63, diante dos fatos o correto seria afirmar que P(Y ≥ 10 kg) < P(Y < 10 kg)
-
Sabe o que é engraçado: depois que passar não se faz NADA com essa matéria.
-
O negócio é o seguinte, anota no caderno e grava na cabeça!
http://sketchtoy.com/69884108
-
=
e não maior
-
-
Resolução Jhoni Zini
Tempo 33:00
https://www.youtube.com/watch?v=ny-ahIDkAmA&list=PL2PrBeiapz785m9GLV5o_NXp8RnERNXKl&index=5&t=5s&ab_channel=FocusConcursos