-
As proposições compostas do enunciado e da letra C são equivalentes,ou seja:
Se ''p'' corresponde a ''funcionário tem mais de 45 anos de idade'', ''q'' a ''realizar pelo menos um exame médico'' e ''t'' a ''tomar a vacina da gripe'',então temos que p->q^t.
Se tal proposição composta for verdadeira ou falsa,também a proposição ~(q^t) -> ~p = ~q v ~t -> ~p será,respectivamente,verdadeira ou falsa.Isto é,as duas têm tabelas-verdades iguais.
Letra C
-
Guilherme, você é capaz de me explicar por que usou a variável "t" pra resolver a questão, sendo que a letra C não menciona que ele tomou a vacina? Eu testei pela tabela-verdade e a ÚNICA que dá certo é a letra D (p--> q^t). Obrigado!
-
Olá,Vinícius(e outros(as)).
É o seguinte:
1o
Vinícius,realmente não há uma menção à proposição ¨t¨ na letra C, mas a partir de ~q v ~t -> ~p podemos verificar o ¨grau de influência¨ de ¨t¨ na referida opção.
Será que ¨ se o funcionário não realizou nenhum exame médico nos últimos dois anos, então ele não tem 50 anos ou mais de idade¨, independente se ¨t¨ é V ou F ?
Se ~q for V, independente do valor lógico de ~t, a disjunção ~q v ~t será V, e a proposição ~q v ~t -> ~p será V só se ~p for também V.
Portanto:
1-Se o funcionário não realizou nenhum exame médico nos últimos dois anos, então ele não realiza pelo menos um exame médico em algum ano( ou seja, ~q é V).
2- Se não realiza pelo menos um exame médico em algum ano, então, independente de ~t ser V ou F, ele tem mais de 45 anos de idade( de acordo com ~q v ~t -> ~p).
3- Se não tem mais de 45 anos de idade, então não tem 50 anos ou mais de idade.
-
2o:
Cuidado!!!! Há uma ligeira distinção entre ¨realizar pelo menos um exame médico por ano¨ e ¨realizar um único exame médico por ano¨. Esta última não é ¨q¨ nem ¨~q¨!!!!! O ¨realizar pelo menos um exame médico por ano¨, que é ''q'', significa que o funcionário realiza um ou mais exames por ano, e a negativa de ¨q¨nos diz que o funcionário não realiza nenhum exame em algum ano.
De fato, se ele tem entre 55 e 60 anos de idade( ou seja, mais de 40 anos), não podemos afirmar que ele realiza um único exame por ano( mas, sim, que o funcionário realiza pelo menos um por ano).
Por conseguinte, a letra D é falsa.
Aberto a criticas. :)
-
p: o funcionário tem mais de 45 anos de idade
q: o funcionário deverá realizar pelo menos um exame médico todo ano
r: o funcionário deverá tomar a vacina contra a gripe todo ano
p → (q ^ r)
Como a diretriz sempre é cumprida, a expressão acima deve sempre ser verdadeira. A tabela verdade fica assim:
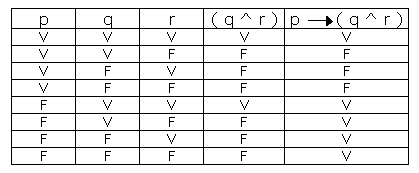
(A) Nessa resposta, está sendo dito que (q ^ r) → p. Um funcionário com idade inferior a 45 anos pode, sem ser obrigado, realizar um exame médico anualmente e tomar a vacina contra a gripe. Portanto, resposta incorreta.
(B) Se ele tem menos que 45 anos, nada se pode afirmar a respeito do funcionário, se ele toma ou não vacina, se ele realiza ou não exame médico anualmente. Portanto, resposta incorreta.
(C) Como o funcionário não realizou nenhum exame nos últimos dois anos, pode-se garantir que ele tem idade inferior a 45 anos. Se a idade dele é inferior a 45 anos, também é inferior a 50 anos, o que torna esse item correto.
(D) O erro deste item é dizer que ele realiza um único exame médico por ano, o que a empresa exige é que se realize pelo menos um exame médico por ano e não apenas um. Portanto, resposta incorreta.
(E) Este item apresenta o mesmo erro do item "A", pois um funcionário com idade inferior a 45 anos pode, sem ser obrigado, realizar um exame médico anualmente e tomar a vacina contra a gripe. Item incorreto.
-
galera,
Acho que não tem nenhuma necessidade de fazer tabelas verdades para casos como esse.
é só pensar nas possibilidades:
a) anualmente realiza um exame médico e toma a vacina contra a gripe, então ele tem mais de 45 anos de idade
Não necessariamente. Pode ser um funcionário com menos de 45 anos que realiza exames e toma vacina todos os anos.
b) tem 40 anos de idade, então ele não realiza exames médicos anualmente ou não toma a vacina contra a gripe.
Não necessariamente. Ele pode ter 40 anos e realizar exames e tomar vacina anualmente.
c) não realizou nenhum exame médico nos últimos dois anos, então ele não tem 50 ou mais anos de idade.
Correta. Se é um funcionário que cumpre as regras, então, se ele não realizou exames, é porque ele ainda não tem a idade pra isso.
d) tem entre 55 e 60 anos de idade, então ele realiza um único exame médico por ano, além de tomar a vacina contra a gripe
Não necessariamente. A questão diz "pelo menos" um exame e não um "único" exame.
e) tomou a vacina contra a gripe ou realizou exames médicos nos últimos dois anos, então ele tem pelo menos 47 anos de idade
Não necessariamente. Nos últimos dois anos funcionários de todas as idades podem ter tomado a vacina e realizado exames.
Bons Estudos!
-
p:um funcionário tem mais de 45 anos
q:realizou pelo menos um exame
r: tomou a vacina contra a gripe
p-> (q^r) = ~(q^r)-> ~p = (~qV~r) ->~p
Se não realizou nenhum exame ou não tomou a vacina contra gripe, então não tem mais de 45 anos.
-
P: Funcionário tem mais de 45 anos de idade.
q: Funcionário deverá realizar exame médico, ao menos 01 por ano (se realizar mais, também será verdadeiro)
r: Funcionário deve tomar vacina.
Passando os termos da linguagem escrita para simbólica temos: P -> q ^r
A questão fala que tudo isso ( P -> q ^r ) é verdadeiro, quando afirma: "Considerando que essa regra seja sempre cumprida,..."
Diante disso, temos: P -> q ^ r = V
O que busca-se agora é saber o valor de cada proposição simples (P, q, r), a partir da proposição composta P -> q ^r (em que a questão já disse ser verdadeira.)
Assim, para descobrir o valor de cada proposição simples, precisa ter o conhecimento das regras e das tabelas-verdade dos operadores CONDICIONAL (->), e do operador CONJUNÇÃO (^).
A regra de partida é saber que o operador CONJUNÇÃO só terá resultado Verdadeiro (verdadeiro porque a questão diz que toda ela é verdadeira), se as proposições simples que a compõe forem obrigatoriamente Verdadeiras, ou seja, se q for Verdadeiro e r também.
Substituindo:
1) P -> q ^r = V
2) P -> (q ^r) = V
3) P -> (V ^V) = V
4) P -> v = V
E isso nos revela que a proposição composta para ser Verdadeira precisa que as simples "q" e "r" sejam verdadeiras.
O segundo momento é a utilização das informações restantes. Para ela, aplica-se as regras do operador CONDICIONAL, ou seja, a sua tabela-verdade ensina que o resultado da proposicao composta de uma implicação ser verdadeiro, os valores das porposições simpoles podem ser tanto verdadeiros como falsos.
P q (P ->q)
v v V
v f F
f v V
f f V
Desse modo, e para finalizar, pode-se retornar da linguagem simbólica para a esrita, e atribuir os valores conseguidos, vejamos:
P: Funcionário tem mais de 45 anos de idade.
q: Funcionário deverá realizar exame médico, ao menos 01 por ano (se realizar mais, também será verdadeiro)
r: Funcionário deve tomar vacina.
P: pode ser v/f, isso mesmo, ou seja, o funcionário poderá ter mais de 45 anos de idade, ou menos, e a proposição composta continuará sendo VERDADEIRA;
porém,
q: só poderá ser verdadeiro, para que a proposição composta seja verdadeira;
r: só poderá ser verdadeira para que a proposição composta seja verdadeira.
Daí, basta analisar cada situação com o que pode, e o que não pode, ser aceito como combinação nas alternativas.
(continua abaixo...)
-
(continuando...)
a) anualmente realiza um exame médico e toma a vacina contra a gripe, então ele tem mais de 45 anos de idade.
ERRADO: realizar exames (q) e tomar vacina (r) podem ser feitos por funcionarios idade menor que 45 (P), ja que essa proposição simples pode também ser falsa.
b) tem 40 anos de idade, então ele não realiza exames médicos anualmente ou não toma a vacina contra a gripe.
ERRADO: realizar exames (q) e tomar vacina (r) podem ser feitos por funcionarios idade menor que 45 (P), ja que essa proposição simples pode também ser falsa.ou seja, quem tem 40 pode tomar vacina POR VONTADE PRÓPRIA, mas com 45 em diante tem que tomar OBRIGADO.
c) não realizou nenhum exame médico nos últimos dois anos, então ele não tem 50 ou mais anos de idade.
CORRETO: atenção! observe que a questão não disse que ele tinha 45, 46, 47, 48 ou 49 anos de idade. Disse que ele tinha nao tinha 50 pra cima. Verdade, que 20, 30 ou 40, nao tem masi que 50, e nao precisa realizar exame ou tomar vacina alguma.
d) tem entre 55 e 60 anos de idade, então ele realiza um único exame médico por ano, além de tomar a vacina contra a gripe.
ERRADO: Cuidado!, O funcionário terá que realiar exames sim, caso tenha mais de 45 anos, e a questao fala de 55 e 60, contudo, a alternativa que limitou em ser um UNICO EXAME, a proposição simples (q) conseiderada verdadeira não diz isso.
e) tomou a vacina contra a gripe ou realizou exames médicos nos últimos dois anos, então ele tem pelo menos 47 anos de idade.
ERRADO: quem tem menos de 45 anos ( P) também pode fazer uma coisa (q) OU ou outra (r), ja que P que é a proposicao que limita a idade, pode ser falsa ou verdadeira.
É isso, Bons Estudos, espero ter ajudado!
Sucesso!
-
Dps q vc fizer tudo isso, seu tempo vai ter acabado... hehe
Eu fiz assim:
Se > 45, então todo ano toma vacina e faz exame(não importa a quantidade)
Eu costumo fazer a comparação: Se sou paulista, então sou Brasileiro.
Paulista = ">45" ; Brasileiro = "todo ano toma vacina e faz exame"
a) anualmente realiza um exame médico e toma a vacina contra a gripe, então ele tem mais de 45 anos de idade.
Se sou brasileiro não quer dizer que sou paulista. Errado
b)tem 40 anos de idade, então ele não realiza exames médicos anualmente ou não toma a vacina contra a gripe.
Se não sou paulista, não quer dizer que não sou brasileiro. Errado
c) não realizou nenhum exame médico nos últimos dois anos, então ele não tem 50 ou mais anos de idade.
Se não sou brasileiro, não tem como ser paulista. ( No caso da questão "50 anos ou mais" está inserido em ">45" ) Certo.
d)tem entre 55 e 60 anos de idade, então ele realiza um único exame médico por ano, além de tomar a vacina contra a gripe.
Neste exemplo, é possível perceber que não tem sentido ele realizar um único exame apenas, quando a questão diz que é pelo menos um exame. Se tivesse : então ele realiza pelo menos um exame... estaria certa.
e) tomou a vacina contra a gripe ou realizou exames médicos nos últimos dois anos, então ele tem pelo menos 47 anos de idade.
Essa não tem nem sentido.
-
Essa questão não está errada, tendo em vista que a alternativa C está incompleta? Porque a alternativa C não em mencionado em momento algum sobre tomar vacina. Quando eu estava resolvendo eu descartei logo a C por estar incompleta depois não encontrei resultados nas outra e fiquei intrigado, quando olho o gabarito, letra C.
-
Questão parece complicada, mas vamos lá:
Traduzindo o enunciado temos: A-->(B/\C)
Usando a propriedade distributiva: A-->(B/\C) é igual a (A-->B)
/\ (A-->C)
Usando a equivalência lógica dentro dos parentes temos: (~B-->~A)
/\ (~C-->~A), depois era só negar a conjunção, porém não precisa porque a questão "C" está incompleta. Dá para resolver tranquilo.
Traduzindo para texto temos: Se não realizou nenhum exame médico,então não tem
mais de 45 anos de idade ou, se não tomou a vacina contra a gripe, então não tem
mais de 45 anos de idade.
Vamos para as questões:
a)
Anualmente realizou um exame médico... (errada! NÃO
REALIZOU NENHUM)
b)
Tem 40 anos de idade... (errada! A questão não afirma
qual é a idade)
c)
Não realizou nenhum exame médico nos últimos dos anos,
então ele não tem 50 ou mais anos de idade. (Correta!)
d)
Tem entre 55 e 60 anos de idade... (errada! Não tem
mais de 45 anos de idade.)
e)
Tomou a vacina contra a gripe ou ... (errada! Não tomou
a vacina)
A grande pegadinha da questão é: a letra C não foi escrita completa.
-
p -> (q/\r) equivale a ~(q/\r) -> ~p, ou seja: ~q\/~r -> ~p
Desse modo, se a afirmação "não realizou nenhum exame" for verdade, então a condição suficiente será verdadeira (isso porque V \/ F é verdade) e a condição necessária também deverá ser (isso porque V --> F é falso). Portanto, se não realizou nenhum exame, então não tem mais de 45 anos. Não ter mais do que 50 anos é, também, não ter mais do que 45 anos.
-
Srs. Se a LETRA C ta certa porque ao tirar a prova na tabela verdade ela não bate??? Pode ate bater nas regrinhas mas a tabela verdade é a prova e a prova ta dando errado, porque a segunda linha da F e pela letra C da V.
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
Alternativa A - INCORRETA. A regra não impede que uma pessoa jovem, com 20 anos, por exemplo, tome a vacina e realize o exame. Assim, o simples fato de a pessoa ter feito o exame e tomado a vacina não permite concluirmos que tem mais de 45 anos.
Alternativa B - INCORRETA. Raciocínio idêntico ao da alternativa anterior. O simples fato de a pessoa ter menos de 45 anos não permite concluir que ela não tenha realizado o exame. Também não permite concluir que não tenha tomado a vacina. A regra não impede pessoas jovens de fazer isso.
Alternativa C - CORRETA. Se a regra obrigava pessoas com mais de 45 anos a fazer o exame, então, se teve alguém que não fez o exame, certamente esta pessoa não tinha mais de 45 anos (e, consequentemente, não tinha mais de 50 anos).
Alternativa D - INCORRETA. Se a pessoa tem entre 55 e 60 anos, então a regra obriga que faça pelo menos um exame por ano (não precisa ser um único exame).
Alternativa E - INCORRETA. Análise idêntica à da alternativa "a".
-
Não consegui entender essa questão.
-
Arthur Lima | Direção Concursos
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
-
Bem complicadinha...
-
Utilizei o raciocínio:
c) não realizou nenhum exame médico nos últimos dois anos, então ele não tem 50 ou mais anos de idade.
p = ele não tem 50 anos de idade;
q = não realizou nenhum exame médico nos últimos dois anos.
isso torna a proposição verdadeira, pois só pode ser falsa se p for verdadeira e q falsa, sem qualquer outra possibilidade. Se tiver algum erro no raciocínio pode corrigir.
grato!
-
Li todos os comentários e não entendi bulhufas!!
-
Errei a questão, mas consegui entender o porquê da certa ser a LETRA C, isso que importa. Vamos em frente!
-
Apliquei a equivalência lógica.
Volta tudo, negando todas, ficando assim:
p-> (q^r) = ~(q^r)-> ~p = (~qV~r) ->~p
-
Para quem errou essa questão diversas vezes, como eu, uma dica: tente resolver através de conjunto.
Lembre-se, na condicional P --> Q, P está contido em Q.
-
Letra C.
O segredo é ter em mente que cada funcionário toma quantas vacinas e realiza quantos exames quiser por ano. Agora, se tiver mais de 45 anos, pelo menos um exame médico e tomar a vacina contra a gripe (mas, se quiser realizar 50 exames no ano, poderá).
-
fiquei feliz em saber que a maioria pensou como eu e errou kkk
-
A alternativa C realmente está correta, se uma das primeiras afirmativas forem falsas, logo ele teria menos de 45 anos, ok
Porém a alternativa D não me parece conter erro algum, quando ele fala em UM ÚNICO exame, está dentro de pelo menos um exame. Na minha visão as duas estão corretas.
-
Por que não pode ser a alternativa A?
-
Raquel Pinheiro, não pode ser a alternativa A porque, na condicional (P-->Q), P está "dentro" de Q.
-
Eu ainda não entendi essa questão.
Pois se é uma CONDICIONAL eu preciso de uma Condição = Resultado, não vice-versa.
Pra mim, o fato do funcionário não ter realizado nenhum exame não garante que ele não tenha mais de 45 (ou 50 como consta na letra C), aliás aqui ele pode ter qualquer idade.
A meu ver, a mais correta entre as opções seria a letra D, onde se cumpre a condição de ter mais de 45 anos e alcança o resultado de realizar um exame médico (onde no enunciado diz que é pelo menos um exame) e toma a vacina contra a gripe.
-
Resolvi por equivalência lógica: sendo a proposição do enunciado P --> Q temos duas equivalências para a condicional (pois é o que a questão está pedindo (equivalência)) ~Q --> ~P (inverte e nega) ou ~P v Q (nega o 1º ou mantém o 2º)
Testando a primeira equivalência ~Q-->~P (inverte e nega) já achamos a alternativa correta.
Quem fez essa questão não dificultou a nossa vida, pois deixou somente alternativas com "se...então..." - daí era só verificar qual cabe na equivalência ~Q --> ~P (inverte e nega).
Costumo simplificar por abreviações para facilitar, a proposição do enunciado ficaria assim: +45 --> EV
(E=Exame e V=Vacina)
Depois é só procurar a alternativa que mais se aproxima da equivalência ~EV --> ~ +45 (inverte e nega)
-
quanto mais estudo isso, menos entendo.....
-
A condicional do enunciado é:
Funcionário tem 45 ou mais --> faz exame E toma vacina
Para essa frase ser verdadeira, todos os funcionários com 45 ou mais anos devem fazer exame e tomar vacina todo ano. Já quanto aos funcionários com menos de 45 anos, nada foi afirmado: eles podem fazer ou não exame, e tomar ou não a vacina.
Se uma pessoa não fez exame, ela não pode ter mais de 45 (pois se tivesse, deveria obrigatoriamente ter feito exame). Portanto, você deve concordar que a frase abaixo é correta:
"Se um funcionário não realizou exame, então ele não tem 45 ou mais anos".
(da mesma forma, poderíamos dizer que "se um funcionário não tomou vacina, então ele não tem 45 ou mais anos").
Entretanto, essa alternativa não aparece entre as opções de respostas. Mas temos uma parecida na letra C:
"se um funcionário não realizou exame, então ele não tem 50 ou mais anos"
Se você concordou com a frase anterior, deve concordar com essa também. Isso porque se alguém não tem 45 ou mais anos, esse mesmo alguém também não tem 50 ou mais anos. Isto é, podemos garantir que uma pessoa que não fez exame TEM MENOS DE 50 ANOS, até porque poderíamos garantir que esta pessoa tem menos de 45 anos.
Resposta: C
Arthur Lima | Direção Concursos
-
eu sempre erro esta questão sempre sempre sempre
-
Pra mim é uma questão de equivalência.
Regras de equivalência do "se...,então":
1° regra: Nega a primeira parte, troca pelo "ou" e mantêm a segunda parte.
2° regra: mantem o conectivo se então, inverte as duas parte e nega tudo. USADA NA QUESTÃO.
-
Eu nunca consigo entender este gabarito, a letra C. Eu nem chego a avaliá-la porque paro na alternativa B que é VERDADEIRA, porque se o empregado tem 40 anos de idade ele NÃO tem mais de 50 anos, o que torna a primeira parte da bicondicional FALSA, o que faz a bicondicional VERDADEIRA para qualquer valor lógico da segunda parte. Parece até que a FCC contratou o CESPE para fazer a questão...
-
Eu acho mais uma questão de logica, vou tentar explicar.
Todo funcionário de 45 anos de idade tem que fazer pelo menos 1 exame e tomar vacina.
a- Anualmente realiza um exame médico e toma a vacina contra a gripe, então ele tem mais de 45 anos de idade.
Não necessariamente, pois pessoas abaixo de 45 anos podem fazer exame e tomar vacina. Não podemos afirmar que tem mais de 45 anos por causa dos exames e vacinas.
b- Tem 40 anos de idade, então ele não realiza exames médicos anualmente ou não toma a vacina contra a gripe.
Não necessariamente, pois funcionários abaixo de 45 anos também podem fazer exames e tomar vacinas. Não podemos afirmar que os funcionários de menos de 45 anos não fazem exames nem tomam vacinas.
c- Não realizou nenhum exame médico nos últimos dois anos, então ele não tem 50 ou mais anos de idade.
Afirmativa correta, pois sabemos que os funcionários com 45 ou mais fazem exames e tomam vacinas, se não realizou nenhum deles nos últimos 2 anos, ou seja, desde os 47, presume-se que este também não teria mais de 45 pois foge da regra.
d- Tem entre 55 e 60 anos de idade, então ele realiza um único exame médico por ano, além de tomar a vacina contra a gripe.
Não necessariamente, pois como anteriormente, funcionários abaixo de 45 anos também podem fazer exames e tomar vacinas.
e- Tomou a vacina contra a gripe ou realizou exames médicos nos últimos dois anos, então ele tem pelo menos 47 anos de idade.
Esta afirmativa esta incorreta pois, deixa claro que o funcionário fez exame OU tomou a vacina, sendo que a regra é fazer exame E tomar vacina.
Esse foi meu jeito para resolver a questão.
Espero ter ajudado!
Grato.
-
Já li todos os comentários e ainda não entendi. '-'
-
Eu só queria saber se essa questão é de equivalência?
-
#Respondi errado!!!
-
Inverte a condicional negando o primeiro termo da nova expressão e terá uma expressão semelhante a letra C
Se Não fizer exame ou Não tomar vacina, então tem mais de 45 anos
-
Matéria chata
-
Trata-se de uma condicional P -> Q ^ R.
P: o funcionário tem mais de 45 anos.
Q: o funcionário deve realizar pelo menos um exame médico.
R: o funcionário deve tomar a vacina da gripe.
Como na condicional o consequente representa um conjunto que abrange o antecedente, sabemos que para o conjunto Q^R, P é um elemento:
Q^R: {x, P, y, ...}
Ou seja, dentre todas as pessoas que tomaram a vacina da gripe e fizeram pelo menos um exame, certamente aquelas que têm mais de 45 anos também fizeram.
Com isso, eliminamos as letras A e B.
A letra D está errada porque nada pode ser dito sobre pessoas que têm entre 55 e 60 anos de idade terem que, necessariamente, fazer um único exame por ano. A questão coloca que, em vez disso, pessoas com mais de 45 anos devem fazer pelo menos um exame por ano.
A letra E também contaria a verdade do enunciado porque se alguém tomou vacina contra a gripe OU realizou exame médico nos últimos dois anos, esse alguém pode ter de 0 a 45 anos tranquilamente, não há nada que leve a concluir que a pessoa tenha 47 ou mais anos.
Por eliminação, letra C.
Para justificar o gabarito sem ser por eliminação, vale consultar o comentário do professor.