-
Primeiramente precisamos saber quais dados da questão podemos usar para resolvê-la. O dado é (1,01)-120 = 0,3 o qual podemos achar o valor de 240 meses que é o nº de parcelas pedido da questão: (1,01)-120 * (1,01)-120 = (1,01)-240
Então achamos o valor de (1,01)-240 = 0,3 * 0,3 = 0,09
Aplicando a Fómula do Fator de Valor Atual para uma série uniforme, sendo VP o valor presente e P a parcela, temos:
VP = P * [1 - (1 + i)-n]/ i ==> 100.000 = P * [1 - (1,01)-240]/ 0,01
100.000 = P * [1 - 0,09]/ 0,01
1.000 = P * 0,91
P = 1.000/ 0,91 = 1.098,901098... = 1,099,00
-
Alguem da area, pode explicar melhor essa questao? Voces conseguiram dar um nó no meu cerebro. Afinal, qual é a resposta correta?
OBRIGADO CONCURSEIROS!!!!!!!!!
-
Confudiram duas cabeças.
-
Temos: 1,01^(-240) = 0,09
e 1,01^(-240) = 1/(1,01^240)
Portanto : 1,01^240 = 1/0,09
Depois disso basta substituir na formula do sistema price.
Bons estudos
-
Valor da Divida = P(prestação) - (1+i)t - P (prestação)
i
100.000 = P - (0,09) - P MULTIPLICA POR ESTAR ANTES DO SINAL DE IGUAL
0,01
1000 = P - 0,09 -P
1000 = 0,91P
P=1000/0,91
P= APROX. 1099.00
assim na questão ele deu o valor a -120 então para achar o 0,09 é so fazer 0,3*0,3 porque 240 é o que a questão quer e é o dobro de 120
LETRA A
TENHO ESSA FORMULA COMO PADRÃO, SEMPRE QUE O EXPOENTE FOR NEGATIVO
-
Trabalhar inicialmente o dado fornecido pela questão:
(1,01) -120 = 0,3
Eu sei que precisarei saber o seguinte valor: (1,01)240 e da matemática básica eu posso desenvolver da seguinte forma:
(1,01)240 =((1,01)120)2 = ((1,01)-120)-2
Substituindo pelo valor dado pela questão:
((1,01)-120)-2 = (0,3)-2 = 1/(0,3)2 = 1/0,09
Ou seja:
(1,01)240 =((1,01)120)2 = ((1,01)-120)-2 = ((1,01)-120)-2 = (0,3)-2 = 1/(0,3)2 = 1/0,09
Calcular agora o valor da parcela usando a fórmula
P= T . (1+i)n . i /(1+i)n – 1
P = 100.000 . (1,01)240 . 0,01/(1,01)240 – 1
A partir daí é só substituir (1,01)240 pelo seu valor que é 1/0,09 e terminar a questão.
MOLEZINHA!!!!
-
Olá,
Vi que a questão gerou muita confusão, então vou tentar dar uma contribuição também, mostrando o jeito que fiz.
A fórmula que devemos utilizar para o sistema frânces é:
P = M (1 + i) n i / (1 + i )n -1
onde:
P = parcela
M = capital tomado
i = juros
n = meses
Então do problema:
P = ?
M = 100.000
i = 0,01
n = 240
Substituindo na fórmula:
P = 100.000 (1,01)240 . 0,01 / (1,01) 240 - 1
Para encontrarmos o (1,01)240:
Sabemos que (1,01)240 =((1,01)120)2
No problema foi dado com o expoente negativo:
(1,01)-120 = 1 / (1,01)120
Assim:
(1,01)120 = 1 / 0,3 = 10 / 3
(10 / 3)2 = 100 / 9
sUBSTITUINDO:
P = 100.000 100/9 . 1/10 / (100/9 - 9/9)
Simplificando:
P= 100.000/91
P= 1.098,91
-
(1,01)^-240= 0,3*0,3 = 0,09;
An_i%= 1-(1+i)^-t/ i = 1-0,09/0,01= 91
prestação= Va/An_i%
prestação = 100.000/91 = 1099
-
Não me aprofundo em mtm, e sou leigo.. mas como estou achando tudo muito complicado, e resolvi a questão seguindo outra linha de raciocínio, vou compartilhar... (não sei se esta certo.. mas cheguei no resultado apróximado): Para quase tudo, utilizo regra de 3, então fiz assim: R$ 1028 x 360 =370.080 (Total pago)Se o imóvel era R$ 100.000 concluí que R$ 270.000 seriam os juros dos 360 meses.
Ai fui pra regra de 3:270.000 esta para 360 assim como x esta para 240
270000 - 360
x - 240
(simplifiquei 360 e 240 por 120 resultado em 3 e 2)270.000 - 3
x - 2 3x = (270.000*2)
3x = 540.000
x = (540.000/3)
x = 180.000 (Este valor deve se referir aos juros em 240 meses)
Assim somamos o principal (Valor do ap) = 180.000 + 100.000 = R$ 280.000
Pra saber a prestação, dividi o valor do AP pelo número de prestações 280.000 / 240 = 1.166
Por aproximação (e achando que como considerei juros proporcionais a 360x, sendo que em período de 240x eles devem ser menores, resultando em um valor menor ao que encontrei) optei pela questão A. Raciocínio tem alguma lógica? Se a taxa de juros fosse muito maior que 1% ele daria um valor muito mais errado ?? Enfim... estou aberto a comentários.
-
Como eu fiz:
Seguindo à risca a fórmula VD = P [(1+ i)^t - 1] / (1+ i)^t . i
Dados do exercício:
VD = 100.000
i = 0,01
t (prestações) = 240
VD = P [(1+ i)^t - 1] / (1+ i)^t . i
100.000 = P[(1+ 0,01)^240 - 1] / (1 + 0,01)^240 . 0,01
100.000 = P(1,01)^240 - 1 / (1,01)^240 . 0,01
100.000 = P(1,01)^240 - P / (1,01)^240 . 0,01
Separando as frações:
100.000 = P(1,01)^240 / (1,01)^240 . 0,01 - P / (1,01)^240 .0,01
'corta' os números iguais / passa o número entre parenteses com a potência para o numerador, assim, o 240 fica negativo, vejamos:
100.000 = P/0,01 - P(1,01)^-240 / 0,01
Agora chegou a hora de trocar, como pede a questão. Ele pede 120, mas temos 240, que é o dobro, então, ao invés de substituirmos por 0,03, vamos substituir pelo dobro, ou seja, 0,09.
100.000 = P/0,01 - 0,09P / 0,01
'P' aqui equivale a um inteiro, então:
100.000 = 0,91P / 0,01
100.000 . 0,01 = 0,91P
P = 1000 / 0,91
P = 1098,90 ... aproximadamente 1099,00
Gente, seguindo a fórmula à risca, colocando os números certinhos nos devidos lugares não tem erro! A não ser que você bobear na hora da divisão, multiplicação, comer um zero, etc.
Fiz dessa maneira porque achei que com fórmula ficaria muito mais fácil de guardar. Vejo vários exemplos, fórmulas diferentes, até mais curtas, tentando levar para um caminho aparentemente fácil, mas que, na minha opinião, acaba confundindo na hora de fazer o exercício e na hora da prova pra lembrar desses 'macetes' acho que vai ser mais complicado do que lembrar da original (fórmula). Por mais que a conta tenha ficado um pouco extensa, pelo menos a probabilidade de ter um erro é menor.
Eu não sei de macetes, nem truques, estudo pelas fórmulas, então por isso estou expondo minha maneira de resolver aqui pra vocês :)
Espero ter ajudado, bons estudos.
-
Formula: P=C [(F*i)/(F-1) substituindo: C: 100.000 -- F (^-1):0,3x0,3=0,09>(1/0,09)=11,1111 -- i=0,01 -- P=100.000 [(11,11x0,01)/ (11,11 -1)]-- P= 100.000 (0,111 / 10,111) -- P=100.000 (0,01098) -- P= 1.098
---- Obs.: F= (1+i)^t
-
Nesta
questão, precisamos calcular o valor da prestação reduzindo-se o prazo para o
valor pedido no enunciado, que é de 240 prestações (meses).
Trabalhando
o dado oferecido no enunciado, (1,01) -120 = 0,3 teremos:
(1,01)
-120 = 0,3 → (1,01)
120 = 10⁄3
(1,01)240 = (1,01)120. (1,01)120 =10⁄3 .10⁄3 = 11.11
Seja P o
valor do nosso financiamento, R o valor da nova prestação, n o prazo e i a
taxa, vamos aplicar a fórmula abaixo:
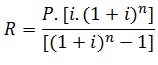
Substituindo
na fórmula acima os valores dados no enunciado:
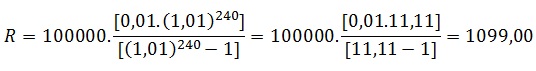
Logo a
resposta certa é a letra A.
-
temos que P=vf(i(1+i)^t/(1+i)^t-1 substituindo P=100000(0,01(1,01)^240/(1,01)^240-1 se 1,01^-120=0,3=3/10 então 1,01^120=10/3 e=1,01^240 = (1,01^120)^2 então = 100/9 que é aprox=11,11. subst na fórmula: P=100000(0,01.11,11/11,11-1) P=100000(0,1111/10,11) P=100000. 0,010989 P=1098,90. resposta certa A.
-
1.028,00 x 360 meses = 368.000 (aprox)
Se 368.000 equivale a 460% (100% do capital + 360% do juro- 1% ao mes), quanto seria 340%(100% do capital +240 % (1% ao m)
obs.: 360 meses x 1% = 360% - 240 meses x 1% = 240%
regra de três 368000 - 460%
x - 340% (resposta 272.000)
bom, 272.000 dividido por 240 = 1.133,333 (valor aproximado da alternativa A)
-
ibrahim silva, tu bebeste foi ???
-
price c*i/1-fator
fator(0.3*0.3)
100000*0.1/1-0.09
resposta a
-
Basta transformarmos para:
(1,01)^(−120) = 0,3; então: (1,01)^(120) = 10/3;
sabemos que (1,01)^(240) = (1,01)^(120) . (1,01)^(120) = 10/3 x 10/3 = 100/9 = 11,11
R = P . [(1+i)^n . i] / [(1+i)^n - 1], onde:
P = valor do financiamento de R$ 100.000,00;
R = valor da nova prestação, pedida na questão;
n = prazo de 240 meses
i = taxa efetiva mensal de juros de 1%
R = 100.000 . [(1,01)^240 . 0,01] / [(1,01)^240 - 1] =100.000 . [11,11 . 0,01] / [11,11 - 1] = 1.099,00; letra A
-
Por esta fórmula deu certo:
P = C . ( (i) ) / 1 - F
P = 100.000 ( 0,01) / 0,91
P = 1.098,90 ( aprox.)
Obs. É SEMPRE BOM SABER OUTRAS FÓRMULAS PARA RESOLVER A MESMA QUESTÃO
-
Dado: (1,01) -120 = 0,3
Dado: (1,01) -240 ============> 0,3 * 0,3 = 0,09
1 - 0,09 = 0,91
100.000/91=
a partir desse momento o candidato precisa apenas calcular os dois primeiros números do quociente, pois as alternativas não são iguais a partir do segundo número
1.000/91 = 10....
A
-
https://exatasparaconcursos.wordpress.com/2013/12/23/caixa-economica-2012-parte-1/
-
Precisamos simplesmente calcular o valor da prestação, reduzindo-se o
prazo para 240 meses. Assim como nas provas da Cespe, é dado um fator
elevado em um expoente negativo. O examinador tenta levar o candidato
inexperiente ao erro, contudo, basta sabermos um pouco de exponenciais,
que fugimos dessa fria:
Basta transformarmos para:
(1,01)^(−120) = 0,3; então: (1,01)^(120) = 10/3;
sabemos que (1,01)^(240) = (1,01)^(120) . (1,01)^(120) = 10/3 x 10/3 = 100/9 = 11,11
R = P . [(1+i)^n . i] / [(1+i)^n - 1], onde:
P = valor do financiamento de R$ 100.000,00;
R = valor da nova prestação, pedida na questão;
n = prazo de 240 meses
i = taxa efetiva mensal de juros de 1%
R = 100.000 . [(1,01)^240 . 0,01] / [(1,01)^240 - 1] =100.000 . [11,11 . 0,01] / [11,11 - 1] = 1.099,00; letra C.
-
Fiz da seguinte forma:
A = P.ain
A-> Valor Atual
P-> Prestação
ain-> Coeficiente
ain= 1- (1+i)^-n/i
1º passo: Encontrar ain
ain= 1-(1+0.01)^-240/0,01
ain= 1/0,01 - ((1+0,01)^-120)^2/0,01
ain= 1/0,01 - 0,3^2/0,01
ain= 1-0,09/0,01
ain= 0,91/0,01
ain= 91
2º Passo: Encontrar A=P.ain
100000=P.91
P= 100000/91
P= 1098,90 aprox. 1099,00
R.: Letra A
-
A: valor atual/valor presente líquido/valor a ser financiado
P: valor da parcela
i: taxa de juros
n: quantidade de parcelas
OBS: a fórmula abaixo é usada para casos em que todas as parcelas são iguais.
I) A = P*[1+(1+i)^-n]/0,01
I) 100000 = P*[1-(1+0,01)^-240]/0,01
I) 100000 = P*[1-(1,01)^-240]/0,01
(1,01)^-240 = [(1,01)^-120]*[(1,01)^-120]
(1,01)^-240 = 0,3 * 0,3
(1,01)^-240 = 0,09
I) 100000 = P*[1-0,09]/0,01
I) 100000 = P*0,91/0,01
I) 100000 = P*91
I) P = 100000/91
I) P = 1098,901...
O valor da prestação é, em reais, aproximadamente 1099,00
-
Existem duas fórmulas para encontrar o fator de valor atual (não adianta fazer mimimi, tem que memorizar essas fórmulas), uma delas é com o expoente do número de períodos negativo (vou utilizar ela por se adequar melhor aos dados fornecidos pela questão):
Fórmula do valor presente (é o valor do empréstimo/financiamento) em séries de pagamento:
Valor presente (atual) = P(prestação) x a (n,i)
Ou seja:
100.000 = P (prestação) x a (n,i)
a (n,i) = fator de valor atual
a (n,i) = 1 - (1 + i) ^ -n / i
Manipulando o dado da questão ( 1,01 ^ -120 = 0,3 ) através de uma das propriedades de potências conseguimos encontrar o fator de valor atual, depois é só jogar na fórmula do valor presente em séries de pagamento e resolver os cálculos:
Propriedade de potências:
(2 ^ 4) ^ 3 =
2 ^ (4 x 3) = 2 ^ 12
Portanto:
( (1,01) ^ -120 ) ^ 2 = (1,01) ^ -240
(0,3) ^ 2 = (1,01) ^ -240;
(1,01) ^ -240 = 0,3*0,3 = 0,09;
a (n,i) = 1 - (1,01) ^ -240 / 0,01
a (n,i) = 1 - 0,09 / 0,01
a (n,i) = 91
Valor presente (atual) = P(prestação) x a (n,i)
100.000 = P (prestação) x 91
P = 100.000 / 91
P = 1.099,00 (aproximadamente)
Gabarito = A
-
Vp=Pmt.[Ani]
Ani=A120;1% = (1-(1+i)^-n)/i...(1-(1+0,01)^-120)/0,01....(1-((1,01)^-120)^2)/0,01....(1-((0,3)^2))/0,01...(1-0,09)/0,01...0,91/0,01=91
Vp=Pmt.[Ani] => Pmt = 100.000/91 = 1098,9 --LETRA A
-
Dados fornecidos pelo item:
• Um imóvel de 100 mil reais é financiado em 360 prestações mensais, a uma taxa de juros de 1% ao mês, pelo Sistema de Amortização Francês (Tabela Price), gerando uma prestação de R$ 1.028,61;
• Reduz-se o prazo do financiamento para 240 prestações;
• (1,01) -120 = 0,3
Note que a banca informa alguns dados em seu enunciado, sendo eles:
Valor presente = VP = R$100.000,00;
j = 1% ao mês;
Número de prestações = n = 240.
Note que quando a questão quer saber qual será o valor de cada prestação.


Resposta: A
-
QUE DESGRAÇA DE QUESTÃO N DA TEMPO DE FAZER NA HORA DA PROVA ESSA CARNIÇA NÃO
-
Se vai pagar a dívida em menos tempo (em 240 meses e não mais em 360 meses), então o valor da parcela diminui, pq vão correr menos juros. E só há uma alternativa para uma parcela menor que R$ 1028,61, que é a letra A.