Questões de Proposições Simples e Compostas e Operadores Lógicos

ID

5389

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2006

Provas

Disciplina

Raciocínio Lógico

Assuntos

Sabendo que as proposições p e q são verdadeiras e que as proposições r e s são falsas, assinale a opção que apresenta valor lógico falso nas proposições abaixo.

Alternativas

Comentários

http://www.geocities.com/puc3ware/operacoes-proposicao.html

p=v; q=v; r=f; s=f

a)~f=>v ^ v; v=>v; v
b)(f=>f) ^ (p ^ q); (v) ^ (v); v ^ v; v
c)(f f) (v v); (v) (v); v v; v
d)~((f => v) V (f => v)); ~((v) V (v)); ~(v V v); ~(v); f
e)f => v (~v f); v (f f); v v; v
p=q=verdade, r=s=falso
a)
Se (não r) então ...
como r = falso, (não r) = verdade
Se (não r) tivesse sido falso, já saberíamos que o resto seria verdade, porque Se falso então qualquer coisa é verdade.
Mas como foi verdadeiro, temos que verificar o resto.
se (verdade) então p e q,
se (verdade) então (verdade e verdade).
(verdade e verdade) = verdade.
se (verdade) então verdade = verdade.
Reposta = verdade.

b)
(se falso então s) e (verdade e verdade)
como se falso então qualquer é verdade,
(r->s) = verdade.
verdade e verdade = verdade.
(verdade) e (verdade) = verdade.
resposta = verdade.
c)
(falso se somente se falso) se somente se (verdadeiro se somente se verdadeiro)
falso falso = verdadeiro.
Ex: 2=5 8=1 (é verdadeiro)
verdadeiro se somente se verdadeiro = verdade
(verdadeiro) se somente se (verdadeiro) = verdade
d)
(r->p): se então XXX. r = falso, se falso então XXX = verdade.
(s->q): se falso XXX. s = falso, se falso então independente do valor de q, (r->q = verdade.
~( (verdade) ou (verdade)) = ~(verdade).
~verdade = não verdade = falso.

e)
Como a questão queria saber qual apresentava valor lógico falso, se (d) é a resposta correta, então não precisamos tentar resolver a letra (e), pois sabemos que somente uma está correta.

Mas para ajudar quem estuda, lá vamos nós:
e)
(r->s): se r então q. se (falso) então (xxx) é sempre verdade independente do valor de xxx. (r->s) = verdade.
~p = não verdade = falso.
(~p r) = (falso falso) = verdade
(verdade) verdade : verdade se somente se verdade = verdade.

Para resolver estas questões é essencial conhecer as tabelas verdades das operações:
-> : se ... então ...
~: não
: se e somente se

Tabela de ->
V->V=V
V->F=F
F->V=V
F->F=V
Ou ainda, F->X=V (Se falso, então indendente do próximo valor, o resultado é verdade).

Tabela de ~
~V=F
~F=V

Tabela de
VV = V
VF = F
FV = F
FF = V

Bons estudos...
Tabela VerdadeA____B____(A^B)____(A v B)____(A->B)____(A<->B)V____V______V_________V_________V__________VV____F______F_________V_________F__________FF____V______F_________V_________V__________FF____F______F_________F_________V__________Vr=Fs=Fp=Vq=Va)~F->V^V A negação de F=V. Observe na tabela A=V e B=V (A^B)=VV->V = Observe na tabela A=V e B=V (A->B)=V (valor lógico verdadeiro)b)(F->F)^(V^V)Observe A=F e B=F (A->B)=V. Observe A=V e B=V (A^B)=VV^V Observe A=V e B=V (A^B)=V (valor lógico verdadeiro)c)(F<->F)<->(V<->V) Observe A=F e B=F (A<->B)=V. Observe A=V e B=V (A<->B)=VV<->V Observe A=V e B=V (A<->B)=V (Valor lógico verdadeiro)d)~((F->V)v(F->V)) Obsrve A=F e B=V (A->B)=V. ~(V v V) Observe A=V e B=V (A v B)=V~V (Negação de verdade=F, valor lógico FALSO)e) F->V<->(~V<->F) Observe A=F e B=V (A->B)=V. Observe ~V=FV<->(F<->F) Observe A=F e B=F (A<->B)=VV<->V=V (Valor lógico verdadeiro)Gabarito (d)
Alternativa d.

Análise das alternativas

Sabe-se que: VAL (p) = V; VAL (q) = V; VAL (r) = F; VAL (s) = F; onde VAL = valoração.

Substituindo as proposições por seus respectivos valores lógicos:
- a)
- V - - > V ^ V
- V - - > V
V
- b)
- (F - - > F) ^ (V ^ V)
- V ^ V
- V
- c)
- (F < - - > F) < - - > (V < - - > V)
V < - - > V

V
- d)
- ¬ ((F - - > V) v (F - - > V))
¬ ( V v V )

¬ V )

F
- e)
- F - - > V < - - > (F < - - > F )
- V < - - > V
- V
Bons Estudos!
Questão boa pra treinar.

ID

10708

Banca

ESAF

Órgão

ANEEL

Ano

2004

Provas

ESAF - 2004 - ANEEL - Técnico Administrativo

Disciplina

Raciocínio Lógico

Assuntos

Surfo ou estudo. Fumo ou não surfo. Velejo ou não estudo. Ora, não velejo. Assim,

Alternativas

estudo e fumo.

não fumo e surfo.

não velejo e não fumo.

estudo e não fumo.

fumo e surfo.

Comentários

Vamos deduzir a questão…. De uma maneira simples e pratica…. Separe em duas colunas, A e B (que correspondem às duas possibilidades do evento)

Primeiro Passo - Surfo ou Estudo (Sabemos que ele não pode surfar e estudar, logo colocamos um em cada Coluna)

Segundo Passo – Fumo ou não Surfo (Sabemos que se ele não surfa ele estuda, logo ou ele fuma ou ele estuda e se ele fuma entao ele não estudo logo ele surfa)

Terceiro Passo - Velejo ou não estudo (Sabemos que se ele não estuda ele surfa, logo ou ele Veleja ou ele Surfa, portanto se ele Veleja ele estuda)

A - Surfa / Fuma
B - Estuda / Veleja

Portanto ou ele Estuda e Veleja ou ele Surfa e Fuma, como ele diz que não veleja, podemos deduzir que ele surfa e fuma.
S:Surfa E:Estuda F:Fuma V:Veleja

Premissas:
S v E
F v ~S
V v ~E
Ora ~V

Primeiro:
Ora ~V >>Verdade

Segundo:
V(falso)v ~E(verdade)>>Verdade

Terceiro:
S(Verdade)v E(Falso) >>Verdade

Quarto:
F(Verdade)v ~S(Falso) >>Verdade

Conclusões Verdadeiras:
~V
~E
F
S
Alternativa e.

Considerando as premissas verdadeiras:

I - Surfo ou estudo. (V)

II - Fumo ou não surfo. (V)

III - Velejo ou não estudo. (V)

IV - Ora, não velejo. (V)

Pela proposição IV (em negrito):

Velejo (F) ou não estudo (V). (V)

Explicação:a negação da proposição em negrito é F e, como III é uma disjunção ("ou" - v), "não estudo" possui valor lógico V; isto é, para se garantir que uma disjunção seja V, há necessidade de que pelo menos uma proposição seja V.

I:

Surfo (V) ou estudo (F). (V)

A proposição com realce cinza é F, uma vez que é a negativa de "não estudo"; assim, "Surfo" possui valor lógico V para se garantir a veracidade de I.

Finalmente, II:

Fumo (V) ou não surfo (F). (V)

De novo, temos uma disjunção "ou" e, a proposição com realce verde é F, pois, é a negação de "Surfo"; desta forma, "Fumo" é necessariamente verdadeira.

Conclusão:

Fumo.

Surfo.

Não estudo.

Bons Estudos!
Gente, é só saber operar com as equivalências. Vocês estão complicando demais. Na hora da prova, quase ninguem tem cabeça pra raciocinar sobre variaveis. Vejam:
As proposições são do tipo (P v Q), que apesar de não ter uma forma equivalente, é parecida com a equivalente de uma proposição condicional (P -> Q), ou seja, é parecida com (~P v Q). É só reescrever nessa forma:
1) Surfo ou estudo.
~p = surto
q = estudo
p - >q = se não surto, estudo
(obs.: observe que não surtar é P, que é o contrário de ~P. Racicionio semelhante para as proposições abaixo)
2) Fumo ou não surfo.
~p = fumo
q = não surfo
p - >q = se não fumo, não surfo
3) Velejo ou não estudo.
~p = velejo
q = não surfo
p - >q = se não velejo, não surfo
Ora, não velejo
Consequencias de não velejar:
a) Não estuda
b) Surfa
c) Fuma
Resposta: E
Ou

Basta uma verdadeira para a premiss ser verdadeira.
1) Surfo OU estudo
2) Fumo OU Não surfo
3) Velejo OU Não estudo
4) Não velejo.
Partindo-se da premissa 4, que a questão afirma ser verdade que Não Velejo, temos:
3) F OU V
2) V OU F
1) V OU F
Logo, a resposta é Surfo e Fumo, não no meu caso...fé.
Esse cara não é concurseiro...
Surfa, fuma e não estuda! rsrsr
Esse ou é "disjuntivo"... Equivale ao "OU OU"
Então fiz uma tabelinha e fui cortando...
Ficou assim!
Resolução desta questão no Canal Matemadicas! Segue o link do vídeo explicativo:

https://www.youtube.com/watch?v=YIRuJ3SvaIM&index=3&list=PLBJoykwJ-tr1PS2sctioKO_9FgsB3s4Nl
Surfo ou estudo = V
V ou F = V
Fumo ou não surfo = V
V ou F = V
Velejo ou não estudo = V
F ou V = V
Não velejo = V

GABARITO -> [E]
Método Telles :)
De fato temos que saber que (não velejo é verdadeira e onde disser o contrário será falsa.)
No(OU)onde tiver falsa a outra tem que ser verdadeira.

Surfo ou estudo.
Fumo ou não surfo.
Velejo ou não estudo.
Ora, não velejo

GABARITO E
Assumindo que premissa formada por uma proposição simples (“não velejo”) é verdade, podemos voltar analisando as demais premissas do argumento:

Velejo ou não estudo.
A primeira parte desta proposição (“velejo”) é falsa. Portanto, a segunda parte precisa ser verdadeira (“não estudo”), para que esta disjunção seja verdadeira. Portanto, de fato eu não estudo.

Surfo ou estudo.
A segunda parte desta proposição (“estudo”) é falsa, pois já vimos que não estudo. Assim, a primeira parte precisa ser verdadeira, para que a disjunção seja verdadeira. Ou seja, surfo.

Fumo ou não surfo.
Novamente, a segunda parte dessa disjunção é falsa. A primeira precisa ser verdadeira. Isto é, fumo.
Com isto, vemos que:
- não estudo
- surfo
- fumo

Resposta: E
1º Assumimos que todas as premissas são verdadeiras
2º Começamos da proposição simples ''Ora, não velejO''.
3º O meu ficou assim:

Surfo (V) ou estudo (F) = V [DISJUNÇÃO SIMPLES]
Fumo (V) ou não surfo (F) = V [DISJUNÇÃO SIMPLES]
Velejo (F) ou não estudo (V) = V [DISJUNÇÃO SIMPLES]
Ora, não velejO (v) = V [PROPOSIÇÃO SIMPLES]
Assumindo que todas as proposições são verdadeiras. Então tem-se:
P:velejo
Q:fumo
S:surfo
E:estudo
S v E (surfo ou estudo) = verdadeiro; Q v ~S (fumo ou não surfo) = verdadeiro; e assim por diante.Voltando a regra das proposições, a gente precisa os valores lógicos para que cada proposição seja verdade.

A questão afirma que "não velejo" é verdadeira. Então:
~P = V
Por isso, na proposição "velejo ou não estudo" P = F e consequentemente (para que a sentença seja verdadeira) ~E = V
P v ~E = Verdadeira, se P = falso e ~E = verdadeira.
Fazendo isso com todas as sentenças tem-se que:
P:velejo (falso)
Q:fumo (verdadeiro)
S:surfo (verdadeiro)
E:estudo (falso)

Concluindo a questão, a alternativa que apresenta a sentença com valor logico verdadeiro é ~P -> Q ^ S (não velejo, assim fumo e surfo) ALTERNATIVA CORRETA LETRA E
MÉTODO DO PROFESSOR TELLES

PONTAPÉ:

ORA, NÃO VELEJO!
--------------------------------------------------------------------------------------------------------------------------------------
-> VELEJO (NEGOU, ENTÃO FALSO! CIRCULE "NÃO ESTUDO") (FALSO)
OU
-> NÃO ESTUDO (VERDADEIRO)
--------------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------------
-> SURFO (ESTUDO É FALSO, ENTÃO "SURFO" É VERDADEIRO)
OU
-> ESTUDO (COMO ACIMA NÃO ESTUDO É VERDADEIRO, "ESTUDO" É FALSO)
--------------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------------
-> FUMO (VERDADEIRO, POIS "NÃO SURFO" É FALSO)
OU
-> NÃO SURFO (COMO SURFO É VERDADEIRO ACIMA, ENTÃO "NÃO SURFO" É FALSO)
--------------------------------------------------------------------------------------------------------------------------------------

VERDADEIRO -> "NÃO ESTUDO", "SURFO" E "FUMO"
FALSO -> "VELEJO", "ESTUDO" E "NÃO SURFO"

Apenas a alternativa E é correta, pois é verdadeiro que ele SURFA E FUMA.

Espero ter ajudado!
Gabi aqui!

Primeiro: Considere todas as premissas verdadeiras, independente do conectivo...

Ora, "não velejo". Se essa afirmativa é verdadeira, logo, consigo classificar as premissas começando por "velejo". Se velejo é falso, logo, não estudo tem que ser verdadeiro para afirmativa ser verdadeira. E assim por diante. OBS: no conectivo OU tudo F dá Falso mas, como eu quero tornar a afirmativa verdadeira, pelo menos uma tem que ser verdade.

Surfo (V) ou estudo (F) = V

Fumo (V) ou ñ surfo (F) = V

Velejo (F) ou ñ estudo (V) = V

Portanto: Fumo, surfo e não estudo.
Assertiva E correta

ID

25150

Banca

CESPE / CEBRASPE

Órgão

TSE

Ano

2007

Provas

CESPE - 2007 - TSE - Técnico Judiciário - Área Administrativa

Disciplina

Raciocínio Lógico

Assuntos

Na análise de um argumento, pode-se evitar considerações subjetivas, por meio da reescrita das proposições envolvidas na linguagem da lógica formal. Considere que P, Q, R e S sejam proposições e que "Λ", "V", "¬" e "→" sejam os conectores lógicos que representam, respectivamente, "e", "ou", "negação" e o "conector condicional". Considere também a proposição a seguir. Quando Paulo vai ao trabalho de ônibus ou de metrô, ele sempre leva um guarda-chuva e também dinheiro trocado. Assinale a opção que expressa corretamente a proposição acima em linguagem da lógica formal, assumindo que P = "Quando Paulo vai ao trabalho de ônibus", Q = "Quando Paulo vai ao trabalho de metrô", R = "ele sempre leva um guarda-chuva" e S = "ele sempre leva dinheiro trocado".

Alternativas

P → (Q V R)

(P → Q) V R

(P V Q) → (R Λ S).

P V (Q → (R Λ S)).

Comentários

As proposições p e q que são as formas de como ele vai ao trabalho, não importando se de metrô ou de ônibus, dá uma idéia de opção, representado com o conector logico " V ". Já nas proposições r e s, dão idéia de consequência composta, representados por " ? ". Como toda opção tem consequência, isso é algo condicional. Então, a condição para que se tenha as ações de r e s é que se opte por uma das opções: p ou q .

A alternativa que representa é a "c".
às vezes a Cespe pede apenas para interpretar textos na prova de raciocínio lógico.

De acordo com a questão, a sentença:

"Quando Paulo vai ao trabalho de ônibus ou de metrô, ele sempre leva um guarda-chuva e também dinheiro trocado"

Pode ser resumida a:

"P ou Q, logo R e S"

Usando os símbolos que o enunciado dá:

"P v Q -> R ^ S"

Alternativa C
Só para complementar , a operação condicional muita das vezes aparece na forma de "quando...." em vez de "se ...então"
Ex:Se chove, então faz frio” é o mesmo que dizer que "Quando chove, faz frio."
Entao pode-se dizer que: Quando = -----> (se, entao) assim como a palavra sempre = -----> (se, então)?
Prova hoje.
Comento: Se Paulo vai ao trabalho de ônibus ou de metrô, então ele leva guarda-chuva e dinheiro trocado.
Seja:

P: ônibus

Q:metrô

R: guarda-chuva

S: dinheiro trocado

(PvQ) → (R^S)
O comentário de Tiago Trigo é muito pertinente.
Na boa eu sou muito ruim de RLM mas interpretando o texto acertei. AVANTEEEE pessoal.
GABARITO C

Algumas variações da condicional (➝ "se... então")
- Dado que/ já que = Q ➝ P
- Sempre que P, Q = P ➝ Q
- P a não ser que Q = ~Q ➝ P
- P, pois Q= Q ➝ P
- Como P ocorre, Q ocorre= P ➝ Q
- P somente se Q = P ➝ Q
- P apenas se Q= P ➝ Q
- Desde que P ➝ Q
- Como P ➝ Q
- Quando P ➝ Q
- P Logo Q
- P Consequentemente Q
- Q é uma consequência de/do/da P(invertida) "obs: 'é' não conta verbo"
- P é suficiente para Q (normal)
- P é necessário para Q (invertida)
A caminhada pode ser longa, mas desistir não acelera.

ID

43660

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2008

Provas

Disciplina

Raciocínio Lógico

Assuntos

"O projeto será bem-sucedido se ou o processo de desenvolvimento é o Processo Unificado ou a linguagem utilizada é Java."

Uma possível tradução da sentença acima para a lógica de predicados de primeira ordem é

Alternativas

(Sp → JI) ←→ ( Sp → Ud)

Comentários

Consideremos as seguintes proposições:Sp : O projeto será bem-sucedidoUd : Processo de desenvolvimento é o Processo UnificadoJl : linguagem utilizada é JavaPoderíamos trocar a frase da seguinte formaSe Ud ou Jl então Sp, o que equivale a (Ud ou Jl) implica SpResposta e
Questão igual "Q14551"
Questão igual "Q50302".
Depois de inúmeros exercícios de raciocínio lógico, primeira vez que vejo "... se ou ...". :(
Essa questão mistura Condicional com Disjunção EXCLUSIVA! Se alguem souber qual é a equivalência da Disjunção exclusiva (q acho é o ponto pra resolver a questão), por favor nos informem!
Obrigado
Essa questao nao e' de java. E' Raciocinio Logico
Pessoal do QC, vamos reclassificar por favor
Equivalente da Disjunção exclisiva ou...ou
ou P ou Q = P se e somente se não Q; não P se e somente se Q.
Complementando o 1° comentário, que está correto:
A questão simplesmente inverteu a Condição Suficiente (CS) e a Necessária (CN) de ordem e deixou o "então" implícito, por isso ficou mais "complexa". Veja ela na ordem natural, qual seja, CS -> CN:
SE (ou o processo de desenvolvimento é o Processo Unificado OU a linguagem utilizada é Java) [então] o projeto será bem-sucedido.
Transformando em símbolos, fica: .

Se não soubermos viver juntos como irmãos, pereceremos todos juntos como tontos. (Martin Luther King)
A alternativa menos errada é a "e". Digo isso por que ela possui apenas um erro: utilizar o operador "ou" em vez do "ou exclusivo" que foi requerido. Do resto o comentário anterior explica muito bem.
Não estou certo sobre esta questão.
O enunciado indica a presença de uma CONDICIONAL e de um OU EXCLUSIVO, o que implica, na minha opinião, a seguinte proposição, considerando:
"O projeto será bem-sucedido se ... " CONDICIONAL e
"OU o projeto ... OU a linguagem ..." OU EXCLUSIVO
( ~ ( UD <--> JI ) ) --> SP

Eu tentei chegar a alguma das alternatvas de respostas disponíveis, a partir da proposição sugerida acima, mas não consegui. Notei que se a intenção do enunciado era expor a presença de um OU NÃO EXCLUSIVO, o que consolidaria a questão como mal formulada, e portanto, devendo ser anulada, a tradução seria a da alternativa E a qual é a correta segundo a banca examinadora.
A questão é bem discutível de fato mas, de qualquer forma, podemos descartar 4 respostas pois, das letras a até d, o operador condicional é SE E SOMENTE SE. Sobra apenas a letra e.
Resolvi porque a única questão que apresenta OU jutantamente com SE, ENTÃO é a E, as demais têm SE, SOMENTE SE com OU, e a questão pede OU e SE, ENTÂO. (:
Mozart Fiscal. Vi a mesma falha.... Mas de fato dá pra sair pela "menos errada"
Isso é proposições que a banca esta analisando, (Da lógica de Predicados, temos as variáveis de Aridade) : Nesse caso unário:

Exemplo Gabarito:(Jl v Ud)→Sp

Entendendo melhor Logica de Predicados: https://youtu.be/gMpi4HO2cnY

SINTAXE DA LÓGICA PROPOSICIONAL:

LINK SOBRE : https://medium.com/@felipemaiapolo/logica-prorposicional-l6477238563b

Sobre a questão: "O projeto será bem-sucedido se ou o processo de desenvolvimento é o Processo Unificado ou a linguagem utilizada é Java."

Observação: SE (ou o processo de desenvolvimento é o Processo Unificado OU a linguagem utilizada é Java) [então] o projeto será bem-sucedido.

{Disjução - ou (V)) , {Condicional ou Implicação:se ...então (→) (⇒)

Lembrem-se que a Matemática é uma ferramenta para modelagem e abstração do “mundo real”, e a Lógica pode se constituir na LINGUAGEM pela qual descrevemos fatos e ideias sobre este mundo.

Assim como a Língua portuguesa é uma linguagem e que portanto possui uma gramática e formas de escrever corretamente uma frase que expresse alguma fato ou ideia, também a Lógica possui uma linguagem, com seus elementos e gramática, a que chamamos de SINTAXE da Lógica proposicional.

A sintaxe do Cálculo proposicional especifica os símbolos e os modos de combiná-los para formar uma expressão válida da linguagem, as quais podem ser chamadas de “fórmulas bem formadas”(fbf).

Elementos Válidos:

Letras Sentenciais – p, q, r, s, a, b, etc.

Conectivos ou Operadores Lógicos:
;
Negação – não é o caso que (∼) (¬)

Conjunção – e (&) (∧)

Disjunção – ou (V)

Condicional ou implicação: se ...então (→) (⇒)

Bicondicional: se e somente se (↔) (⇔)

Parênteses (, )

ID

64165

Banca

CESPE / CEBRASPE

Órgão

INSS

Ano

2008

Provas

CESPE - 2008 - INSS - Técnico do Seguro Social

Disciplina

Raciocínio Lógico

Assuntos

Algumas sentenças são chamadas abertas porque são passíveis de interpretação para que possam ser julgadas como verdadeiras (V) ou falsas (F). Se a sentença aberta for uma expressão da forma ∀xP(x), lida como “para todo x, P(x)", em que x é um elemento qualquer de um conjunto U, e P(x) é uma propriedade a respeito dos elementos de U, então é preciso explicitar U e P para que seja possível fazer o julgamento como V ou como F.

Se U for o conjunto de todos os funcionários públicos e P(x) for a propriedade "x é funcionário do INSS", então é falsa a sentença ∀xP(x).

Alternativas

Certo

Errado

Comentários

Quando resolvi errei por falta de atenção.A questão diz que é errado a afirmação "Todo funcionário público é funcionário do INSS" no caso a afirmação é falsa e a QUESTÂO é verdadeira.
Está questão é verdadeira? alguém que entendeu por favor explique melhor porque eu estou com dúvida.Fico no aguardo
A sentença é falsa, pois ela afirma que qualquer que seja o funcionáriopúblico ele é funcionário do INSS.COMO A ASSERTIVA DIZ QUE É FALSA, TORNA-SE VERDADEIRA PARA MARCAÇÃO NO GABARITO.
Alguem poderia explicar melhor essas questão...os comentarios não foram claros
Por favor: alguém pode, por gentileza, postar comentário mais claro sobre a questão.
Agradeço os comentários acima, mas ainda assim não estão muito claros.
ITEM CORRETO. Traduzindo a sentença “todo funcionário publico é funcionário do INSS”. Percebe-se que a a frase não está correta e o item afirma que ela não está.

Esse A de cabeça para baixo se lê "para todo" ou "todo".
Apenas complementando as informacoes do colega acima...
= para todo e qualquer x
P(x) = "x é funcionário do INSS",
logo o enunciado diz que:
Para todo e qualquer x, x e' funcionario do inss, ou Seja, o que o examinador esta perguntando e' se qualquer funcionario(x) e' funcionario do INSS. A afirmacao e' falsa. Mas tem a pegadinha final (foi nessa que eu cai...) Como no enunciado afima que e' falsa... a acertiva e' verdadeira... Questao bem elaborada para testar a atencao de quem realmente esta estudando...
Bons estudos
Questão horrível, a banca deveria especificar o que é X !!!! apenas disse que U é o universo de funcionários publicos, acho que ela quis dizer que x é qualquer funcionario publico, se foi isso a afirmativa é errada mesmo.
MARCO AURÉLIO, TAMBÉM PENSEI COMO VOCÊ, MAS DEPOIS ANALISEI MELHOR E VI QUE A FORMA COMO A QUESTÃO FOI FORMULADA ESTÁ CORRETA, POIS NO ENUNCIADO É POSSÍVEL VERIFICAR QUE "X" É UM ELEMENTO QUALQUER DO CONJUNTO "U", PORTANTO É UM FUNCIONÁRIO PÚBLICO.

VEJA:
..."Se a sentença aberta for uma expressão da forma oexP(x), lida como "para todo x, P(x)",
em que x é um elemento qualquer de um conjunto U,
e P(x) é uma propriedade a respeito dos elementos de U, então é preciso
explicitar U e P para que seja possível fazer o julgamento como V ou como F."
∀xP(x) pode ser lido como: “Para todo funcionário público, pode-se considerá-los funcionários do INSS”, ou “Todo funcionário publico é funcionário do INSS”. O que é uma afirmação falsa, pois existem funcionários públicos que não são funcionários do INSS.

A resposta é : Certo.
Precisei reler umas 10 vezes a questão e eu resolvi da maneira abaixo. O mais importante para mim foi entender o enunciado principal, antes da questão propriamente dita. Ele diz assim:
- "Expressão da forma VxP(x), lida como 'para todo x, P(x)".
- "x é um elemento qualquer de um conjunto U";
- "P(x) é uma propriedade a respeito dos elementos de U".

E a questão diz o seguinte:
- "Se U for o conjunto de todos os funcionários públicos"
- "P(x) for a propriedade "x é funcionário público do INSS"
- "Então é falsa a sentença VxP(x)"

OU SEJA (une os dois entendimentos agora):

- Se "x é um elemento qualquer de um conjunto U" ----> então x = U = todos os funcionários públicos.
- Se "P(x) é uma propriedade a respeito dos elementos de U" -----> então P(x) = funcionário público do INSS.
- VxP(x) ---> Ao pé da letra, a frase fica assim: "Para (V) todos os funcionários públicos (x), funcionários públicos do INSS (Px)."
- Traduzindo: "Todos os funcionários públicos, funcionários do INSS".

E é ERRADO afirmar isso. Ou seja, a questão está CERTA (pq ela afirma que é falso).
Correta.
Primeiro vc tem que saber o que significa os símbolos. A proposição está dizendo simplesmente: Todo funcionário público é funcionário do INSS. FALSA. Mas a questão diz que é falsa. Então a questão em si, da prova, é CORRETA. Desenhe os conjuntos em círculos se for o caso:
( ......Fpúblicos........(...Funcionários INSS....).......Fpúblicos.........)
Certo.

Resumindo.

Não é todo funcionário público que é funcionário do INSS...
Porém a assertiva nega em dizer isso....então é verdade QUE NEM TODO SERVIDOR PÚBLICO É SERVIDOR DO INSS
Certo.

Imagina que isso ai embaixo é um círculo e fica claro que todos do Inss são servidores públicos mas nem todos servidores são do Inss.

( U (P) )

Portanto ∀xP(x) é falso.
sentenças abertas não tem como julgar verdadeiro ou falso. Muito complicada essa questão.
Veja que a frase ∀ x P(x) deste item pode ser escrita como: para todo x
pertencente ao conjunto, x é funcionário do INSS. Ou melhor: todo x pertencente ao
conjunto é funcionário do INSS. Esta frase é realmente falsa, pois o conjunto
referido é formado por TODOS os funcionários públicos, de modo que certamente
alguns deles (ou a maioria) não são funcionários do INSS.
Portanto, o item está CORRETO.
Resposta
Nem todos funcionários publicos são funcionários do INSS!! Portanto sentença falsa.

Gab. certo.
Não entendi essa questão, porque já começa falando que as sentenças abertas são passíveis de interpretação... como assim? até onde eu seu as sentenças abertas não temos como julgar se elas é verdadeira ou falsa, são indeterminadas...
Layla, veja o resto da frase: Algumas sentenças são chamadas abertas porque são passíveis de interpretação para que possam ser julgadas como verdadeiras (V) ou falsas (F). Ou seja, ela têm que ser interpretadas PARA (A FIM DE QUE) que possam ser valoradas como V ou F, se não forem interpretadas não podem ser valoradas. Espero que tenha ajudado. Bons Estudos!
P(x) = x é funcionário do INSS (aquele servidor público é funcionário do INSS) = V
∀ = Para todo ou todo
∀x P(x) = Todo x é funcionário do INSS (todo servidor público é funcionário do INSS) = F

A sentença é falsa pois generaliza
U = TODOS FUNCIONÁRIOS PÚBLICO

P = FUNCIONÁRIOS DO INSS

"NÃO É TODO FUNCIONÁRIO PÚBLICO QUE É FUNCIONÁRIO DO INSS"
∀x: para todo x

P(x): x é funcionário do INSS

U: todos os funcionário públicos

∀xP(x): Todo funcionário público é funcionário do INSS.

O enunciado afirma que é falsa a sentença "∀xP(x): Todo funcionário público é funcionário do INSS". E está certo, pois nem todo funcionário público é funcionário do INSS.

Gab: C.
Pergunta Aberta.
pensei que só sentenças fechadas pudessem ser julgadas como V OU F....
obrigada Danilo Gondim pela explicação.
Gabarito: certo.

O comentário do professor Vinicius Werneck foi o seguinte:

"∀xP(x) pode ser lido como: “Para todo funcionário público, pode-se considerá-los funcionários do INSS”, ou “Todo funcionário publico é funcionário do INSS”. O que é uma afirmação falsa, pois existem funcionários públicos que não são funcionários do INSS."

Como a questão já coloca como sendo falsa a afirmativa ∀xP(x), está correta.

Boa sorte e bons estudos!
Veja que a frase  x P(x) deste item pode ser escrita como: para todo x pertencente ao conjunto, x é funcionário do INSS. Ou melhor: todo x pertencente ao conjunto é funcionário do INSS. Esta frase é realmente falsa, pois o conjunto referido é formado por TODOS os funcionários públicos, de modo que certamente alguns deles (ou a maioria) não são funcionários do INSS. Portanto, o item está CORRETO

Prof. Arthur Lima (Estratégia concursos)
Marco Aurélio, a questão fala "x é qualquer elemento de u"
Certo.
Construindo um diagrama para representar a sentença correta, temos:
O elemento x pode pertencer ao conjunto P, o que pertence também ao conjunto U, mas temos a possibilidade de o elemento x pertencer somente ao conjunto U, o que torna a sentença falsa, uma vez que ser funcionário público não garante ser funcionário do INSS.

Questão comentada pelo Prof. Josimar Padilha
Esse A de cabeça para baixo se lê "para todo" ou "todo".

ID

82432

Banca

CESPE / CEBRASPE

Órgão

EMBASA

Ano

2010

Provas

Disciplina

Raciocínio Lógico

Assuntos

A lógica proposicional trata de argumentações elaboradas por meio de proposições, isto é, de declarações que podem ser julgadas como verdadeiras (V) ou falsas (F), mas nunca como V e F simultaneamente. As proposições normalmente são simbolizadas por letras maiúsculas do alfabeto e alguns símbolos lógicos são usados para compor novas proposições. Uma conjunção, proposição simbolizada por A Λ B, é lida como "A e B" e julgada como V somente quando A e B forem V, e F, nos demais casos. Uma implicação, proposição simbolizada por A➜B, é lida como "se A, então B", e julgada como F somente quando A for V e B for F, e V nos demais casos.

A lógica de primeira ordem também trata de argumentações elaboradas por meio de proposições da lógica proposicional, mas admite proposições que expressem quantificações do tipo "todo", "algum", "nenhum" etc.

A partir dessas notações e definições, julgue o item que se segue.

Considerando que as proposições A, B, B➜C e [A Λ B]➜[C➜D] sejam V, então a proposição D será,obrigatoriamente, V.

Alternativas

Certo

Errado

Comentários

Considere o enunciado correto como:Considerando que as proposições A, B, B->C e[AvB]->[C->D] sejam V, então a proposição D será,obrigatoriamente, V.Montando o esquema todo:A(v)B(v)B(v) -> C(v)[A(v) v B(v)]->[C(v) -> D(v)]------------------------------D(v) = Conclusão verdadeira!
A                                (v)
B                                (v)
[A e B] -> [C -> D]    (v)
resolvendo:
[V e V] -> [V -> D]
[V] -> [V -> D], se o primeiro termo da implicação é V e o segundo termo é V, o resultado será V.
portanto, D deve ser V, vejamos:
[V] -> [V -> V], substituindo D
[V] -> [V], será V. Questão correta.
...Uma conjunção, proposição simbolizada
por AvB, é lida como "A e B"... aqui no caso era pra ser A OU B

O que está em negrito doi erro de digitação do site ou da prova!? Pq se foi da prova cabe recurso!
O erro de digitação muda totalmente o sentido da questão.

Onde tem "B÷C ", na realidade, é B->C. Podem olhar a prova mesmo. Da forma como a questão está, entende-se que B ou C é V. Nesse caso, C poderia ser F. Se C poderia ser F, não necessariamente D precisaria ser V.

Resumindo a conversa, a digitação muda a resposta da questão.
A = V
B = V
C = V

A (V) e B (V) -> C (V) -> D

V -> V --> D

como a proposição é V no antecedente, terá obrigatóriamente ser V no consequente para se tornar correta.

Assim, o valor de D obrigatoriamente será V
Essa questao ta bem maliciosa....

na parte onde tem [A^B] -> [C->D]

Se A ou B for Falso no primeiro colchete isso significa que sera Falso, pois para ser verdadeiro os 2 deve ser V.

ou seja, supondo que o primeiro colchete é falso [A^B], continuando no [C->D], nao necessariamente D deve ser verdadeiro, pois F F no se entao é verdadeiro.

[A^B] -> [C->D]
F    -->     F      = verdadeiro

Mas a questao é clara em dizer que A, B, B ->C sao verdadeiras,

   e que tambem é verdadeiro, logo:
                 V      -->   V          se D for verdadeiro = verdadeiro
                 V     -->    F          se D for falso          = falso

questao correta!!
Eu resolvi de uma maneira bem prática e didática essa questão, só olhar a imagem abaixo
https://scontent-gru2-1.xx.fbcdn.net/hphotos-xpf1/v/t34.0-12/12476332_1044910782215289_810645201_n.jpg?oh=4d193aca6984791f5d33244426b7eeb5&oe=56893C5D
William, seu url não dá certo!
Entendi não
):
nao concordo com a banca, ela faz essa afimaçao pegando todo o conjunto: Considerando que as proposições A, B, B➜C e [A Λ B]➜[C➜D] sejam V, então a proposição D será, logo: ela afrma que D E verdadeira e depois ela fala que D obrigatoriamente tem que V?

depois ela deixa entender que somente A,B,C sao verdadeira e pergunta que obrigatoriamente D E V ? nao entendo pois ela esta fazendo uma pergunta ou seja uma duvida, logo D pode se V ou F
Simples, se D for falso haverá a possibilidade da proposição ser falsa e para a não ocorrência do fato o D deve ser verdadeiro ai não importará os outros valores, pois com D = V será ela sempre Verdade.

ID

105049

Banca

CESPE / CEBRASPE

Órgão

TRE-MG

Ano

2009

Provas

CESPE - 2009 - TRE-MG - Técnico Judiciário - Área Administrativa

Disciplina

Raciocínio Lógico

Assuntos

Proposições são sentenças que podem ser julgadas somente como verdadeiras ou falsas. A esse respeito, considere que p represente a proposição simples "É dever do servidor promover o atendimento cordial a clientes internos e externos", que q represente a proposição simples "O servidor deverá instruir procedimentos administrativos de suporte gerencial" e que r represente a proposição simples "É tarefa do servidor propor alternativas e promover ações para o alcance dos objetivos da organização". Acerca dessas proposições p, q e r e das regras inerentes ao raciocínio lógico, assinale a opção correta

Alternativas

A tabela-verdade completa das proposições simples p, q e r tem 2⁴ linhas.

Comentários

Essa questão aborda a álgebra das proposições. É suficiente, portanto, para sua análise lembrar das propriedades dos operadores lógicos. Vamos lá:a) Correta. A negação de uma proposição composta por disjunções de proposições simples é a conjunção das negações dessas proposições simples. É uma generalização da Lei de Morgan. ~(p v q v r) = ~p ^ ~q ^ ~r.b) Errada. Pois p -> q equivale a ~q -> ~p.c) Errada. Pois, p ^ (q v r) equivale a (p ^ q) v (p ^ r). É a propriedade distributiva da conjunção em relação à disjunção.d) Errada. ~(~(~r)) equivale a ~r.e) Errada. A tabela verdade de uma proposição simples tem apenas 2 linhas.Letra A.Opus Pi.
A tabela verdade tem 8 linhas. 2 elevado ao número de proposições (3).
d) ~(~(~r))<-> r~r <-> r(~r -> r) e (r -> ~r)(r ou r) e (~r ou ~r)r e ~r R: r e ~r (Valor Lógico = Falso. Uma contradição,ou seja, uma proposição que sempre será falsa)
Sangue de Jesus tem poder.
Não entendi nada.............
A confusão aqui se deu (acho) por problema material da questao aqui... ao menos eu me confundi onde acabava a questao e onde iniciavam as alternativas... achei q a primeira equivalência era ainda enunciado.

Dizer que a proposição é equivalente é o mesmo que pedir a negação.

Daí neste caso a minha dúvida persiste só a letra d negaçao da negaçao da negaçao c/ bicondicional... se alguem puder dar o passo a passo... Grata!
Para resolver a questão é necessário entender como funciona a tabela verdade e seus conectivos.
Resumo da tabela verdade com o significado dos conectivos.
“negação = ~”, “e = ^”, “ou = v” , “ou..ou = v”, “equivalente = <=>” , “condicional = ->” , “bicondicional = <->”.
Entendedo a famigerada tabela verdade.
p = V V F F, q = V F V F, p ^ q = V F F F, p -> q = V F V V, p <-> q = V F F V, p v q =F V V F
Obs.: Nesse exemplo utilizamos (2 ? = 2²) 4 linhas. Se fossem 3 letras (p, q, r) a montagem da tabela seria (2 ? = 2³) com 8 linhas.
Resolvendo sem tabela verdade.
Proposições verdadeiras: p, q, r = V
Proposições falsas: ~p, ~q, ~r = F
Simbologia: “~ = negação”, “v = e” , “^ = ou” , “<=> = equivalente”
a) ~(p V q V r) é equivalente a ~p ^ ~q ^ ~r
Resolução:
~(V v V v V) <=> F ^ F ^ F
F v (F v F) <=> F ^ (F ^ F)
F v (F) <=> F ^ (F)
F <=> F
São equivalentes!
Analisando cada alternativa:

a) ~ (p v q v r) = ~p ^ ~q ^ ~ r (Correto).

b) p → q = ~q → ~p (Logo, alternativa errada).

c) p ^ (q v r) = (p ^ q) v (p ^ r) (Logo, alternativa errada).

d) ~(~(~r)) ← → ~r (Alternativa errada).

e) O número de linhas de uma tabela-verdade responde a 2ⁿ, onde n é o número de proposições, aqui temos 3 (p, q, r). Logo teremos 2³ linhas e não 2⁴ linhas (Errado).

RESPOSTA: (A)
Alguém pode explicar detalhadamente?
esse professor não explica naaaaaaaaada. afffffffffffffffffffffff
1º. Nessa questão, especificamente, o texto inicial serviu apenas para identificarmos que existem três proposições (p,q e r).

2º. Devemos analisar alternativa por alternativa para que possamos encontrar a correta, aplicando as regras da equivalência lógica. Vamos lá:

a) ~ (p v q v r) = ~p ^ ~q ^ ~ r

Essa alternativa pede a negação da proposição (p v q v r) que equivale a negar todas as proposições e trocar o conectivo "ou/v" por "e/^". Portanto, alternativa CORRETA.

b) p → q = ~p → ~q

Essa alternativa diz que a proposição p → q equivale a ~p → ~q, sendo que a equivalência correta seria ~q → ~p. Logo, alternativa errada.

c) p ^ (q v r) = p ^ q ^ r

Essa alternativa diz que a proposição p ^ (q v r) equivale a p ^ q ^ r, sendo que a equivalência correta seria (p ^ q) v (p ^ r), ou seja, a equivalência distributiva. Logo, alternativa errada.

d) ~(~(~r)) ← → r

Essa alternativa diz que a proposição ~(~(~r)) equivale a “r”. Nesse caso, basta atribuir um valor lógico a “r” que saberemos que a equivalência correta seria “~r”. Logo, alternativa errada.

e) A tabela-verdade completa das proposições simples p, q e r tem 2⁴ linhas.

Para calcular o número de linhas de uma tabela-verdade basta elevar o numero 2 a potencia referente ao número de proposições. Como temos 3 proposições ficaria 2³ linhas. Logo, alternativa errada.

GABARITO: Letra A
NEGAÇÃO (p v q v r) = ~p ^ ~q ^ ~ r

logo, ~p ^ ~q ^ ~ r EQUIVALE ~p ^ ~q ^ ~ r
CERTA = A
a) ~ (p v q v r) = ~p ^ ~q ^ ~ r
Correto. É só fazer a negação da primeira proposição (p v q v r) !
A negação do "ou" é negar tudo e trocar por ^

b) p → q = ~p → ~q
uma das equivalências do " →" é: ~q → ~p, mas a forma em que foi escrita no item está errada!

c) p ^ (q v r) = p ^ q ^ r
Trata-se de uma propriedade distributiva
o correto seria: (p ^ q) v (p ^ r)
para quem não entendeu : https://www.youtube.com/watch?v=NxVXKiydHvo

d) ~(~(~r)) ← → r
no interior do parêntesis externo, ele quer a negação da negação de r: ~(~r), cuja resposta é r.
Então teremos: ~(r), ou seja, ~r
(ou seja, comece resolvendo de dentro para fora)

e) A tabela-verdade completa das proposições simples p, q e r tem 24 linhas.
temos 3 proposições (p, q e r), por isso devemos elevar o número 2 ao 3: 2³.
2³ = 8 linhas
Resolvi fazendo a tabela verdade.....agora, cá entre nós, que explicação é essa desse professor, seria mais fácil ele colocar assim: "GABARITO A"..... a maior falha do QConcursos é não apresentar vídeos nessas questões de RL como é feito na maioria das de português..... lamentável!
Bons Estudos!!!
a) ~(p\/q\/r) <-> ~p/\~q/\~r

Em ~(p\/q\/r) temos a função OR, a qual só gera resultado negativo se todos os valores forem F, o que acontece somente uma vez na tabela da verdade. Após, usa-se negação (~), a qual inverte qualquer valor que ela precede. No caso, passa todos os valores da table ada verdade para F, sendo que só é V o que era F F F.

EM ~p/\~q/\~r temos a função AND, a qual só é V quando todos os valores forem V. Também só acontece 1 vez, classificando a proposição composta com uma tautologia em relação à 1°;.
Não sabia que na negação também negaria o conectivo...
Acho que uma maneira bem simples de entender essa questão, cuja alternativa correta é a primeira letra, é notar que p v q v r significa simplesmente que ou p ou q ou r é verdadeiro. Portanto é equivalente à sua negação ~ (p v q v r) que nenhuma dessas proposições é verdadeira, nem p nem q nem r, ou seja, todas são falsas, portanto a conjunção de suas negações ~ p ^ ~ q ^ ~ r é verdadeira. Acho que traduzindo o logiquês é isso.
Questão que a primeira vista parece que vai lhe da um trabalhão, mas logo na alternativa "a" você da de cara com uma lei de morgam, uma simples distribuitiva. fácil de resolver.

Moral da historia: Nem tudo que parece ser dificil, é o que realmente é.

ID

141985

Banca

CESPE / CEBRASPE

Órgão

TRE-MT

Ano

2010

Provas

Disciplina

Raciocínio Lógico

Assuntos

Em um debate político, os candidatos A, B e C trocaram acusações entre si.

O candidato A afirmou que B mente. O candidato B disse que A ou C mentem.
O candidato C afirmou que A mente.

Considerando essas informações, os símbolos lógicos anteriormente mencionados e ➜ — que significa "se ..., então" — e ↔ — que significa "se, e somente se" -, e as proposições: P: "Apenas A mente";
Q: "Apenas B mente" e R: "A e C mentem", assinale a opção correspondente à proposição que é valorada como verdadeira.

Alternativas

Comentários

A diz: "B mente"B diz: "A ou C mentem"C diz: "A mente"A única possibilidade das afirmações não se contradizerem é:A menteB diz a verdadeC diz a verdadeEntão.V(P) = VV(Q) = FV(R) = Fa) V e F = Fb) F ou F = Fc) ~P v Q --> F ou F = Fd) V ou F --> V e F ... V --> F = Fe) V e F <--> F ou F ... F <--> F = V:)
I - A afirmou que B mente
1º situação: A fala a Verdade: concluimos que B fala a Mentira
2ª situação: A fala a Mentira: concluimos que B fala a Verdade
II - B disse que A ou C mentem
1º situação: B fala a Mentira. Para ser Falso o que B fala, então os dois tem que ser falso (ver tabela da disjunção), ou seja: A mentir ou C mentir tem que ser falso, portanto A fala a Verdade ou C fala a verdade
2ª situação:B fala a verdade. Para ser Verdade o que B fala, basta um dos dois temos ser Verdadeiro (ver tabela da disjunção), ou seja:
* A fala a Verdade ou C falar a Verdade
* A fala a Verdade ou C falar a Mentira
* A fala a Mentira e C fala a Verdade
Como vimos que A fala a Mentira então o C só pode falar a Verdade
III - C afirmou que A mente
1º situação: C fala a Verdade. Se C fala a Verdade ele diz que A fala a Mentira, mas vimos no início da questão que A fala a Verdade. Então há uma contradição e essa não será nossa resposta. Passemos para 2ª situação
2ª situação: C fala a Verdade e A fala a Mentira
Conclusão geral: A fala Mentira, B fala Verdade e C fala Verdade;
---------------------------------------------------------------------
Contnuando...
P: Apenas A mente --> Verdadeiro
Q: Apenas B mente --> Falso
R: A e C mentem --> Falso

Agora é só resolver nas altern
Supondo que o candidato A diz a verdade, concluímos que:

Candidato C mente, pois ele afirma que o candidato A mente.

Candidato B mente, então A e C falam a verdade. (Temos aqui uma inconsistência, pois vimos que C mente!)

Assim chega-se a conclusão que o candidato A mente. Logo A mente e B, C falam a verdade, com isso as proposições Q e R são falsas e P é verdadeira. Testando cada alternativa:

a) V ^ F = F

b) F v F = F

c) ~[V ^ (~F)] = ~[V ^ V] = ~ V = F

d) V v F ➜ V ^ Q = V ➜ F = F

e) V ^ F ↔ (~V) v F = F ↔ F v F = F ↔ F = V

Reposta: Alternativa E.
Nao entendi nada, mesmo lendo os comentarios dos colegas.
Gab> E
FERNANDA, AS PROPOSIÇÕES FICARAM ASSIM:

P: Am APENAS
Q: Bm APENAS
R: Am ^ Cm

DUAS PROPOSIÇÕES SIMPLES E UMA COMPOSTA... DEVEMOS ESCOLHER UMA DAS SIMPLES A ATRIBUIR O VALOR LÓGICO:

P: Am APENAS = VERDADEDEIRA
Q: Bm APENAS = ......
R: Am ^ Cm

''P'' SENDO VERDADEIRA OBRIGATORIAMENTE ''Q'' SERÁ FALSA POR CONTA DO ''APENAS''... INDO PARA A ''R'' FICARÁ V ^ F QUE É IGUAL A FALSO.

P: Apenas A mente --> Verdadeiro
Q: Apenas B mente --> Falso
R: A e C mentem --> Falso

INDO PARA AS ALTERNATIVAS, SUBSTITUÍMOS OS VALORES:

A - P^Q = V^F = FALSA (ERRADO)
B - QvR = FvF = FALSA (ERRADO)
C - ~[P^(~Q)] = ~(V^V) = (F^F)= FALSA (ERRADO)
D - PvR --> (P^Q) = VvF --> (V^F) = V-->F = FALSA (ERRADO)
E - P^Q (~P)vQ = V^F FvF = F F = VERDADEIRO (GABARITO)
não entendi
eu posso definir, então, quantos falam a verdade? Pois se houve uma inconsistência, essas afirmações não servem.
MUITO DIFÍCIL, GALERA!!!

Só consegui matar essa questão com a dica do colega Vinicius Menti: em 5 minutos você resolve a parada.

Primeiro, monte uma tabela com os candidatos na vertical e horizontal.

Depois, fixe o mentiroso na linha vertical e, horizontalmente, examine as falas de cada candidato.

No final, o mentiroso será aquele da linha horizontal que contiver APENAS 1 F.

A: B mente; A B C

B: A ou C mentem; A   F   V V

C: A mente.   B V   F F

  C F V   F

* Explicando a tabela:

Na 2ª linha, o candidato A foi fixado como mentiroso.

→ A (1ª lin / 2ª col) disse que "B mente". Se ele é o mentiroso, então o que ele disse é mentira (F da 2ª lin / 2ª col);

  → B (1ª lin / 3ª col) disse que "A ou C mentem". Então diz a verdade, porque quem mente é A (V da 2ª lin / 3ª col);

→ C (1ª lin / 4ª col) disse que "A mente". Então diz a verdade, porque quem mente é A (V da 2ª lin / 4ª col).

Segue-se o mesmo raciocínio nas demais linhas, fixando, um por um, os demais candidatos como mentirosos e analisando as falas de cada candidato na horizontal.

Como se vê na tabela, a linha que contem apenas 1 F é o do candidato A. Logo, apenas A mente.

Se apenas A mente, então somente a proposição P é verdadeira, pois P sendo excludente, Q e R tornam-se proposições falsas.

A) P ^ Q B) Q v R C) ~[P ^ ( ~Q )]   D) (P v R) → (P ^ Q)   E) (P ^ Q) ↔ [(~P) v Q)]

V ^ F = F   F v F = F   ~(V ^ V)    (V v F) → (V ^ F) V ^ F F v F

  F v F = F   V → F = F        F    ↔     F = V

* GABARITO: LETRA "E".

Abçs.
O candidato A afirmou que B mente.
Opções 1: A mente e B fala a verdade ou B mente e A fala a verdade
O candidato C afirmou que A mente.
Opções 2: A mente e C fala a verdade ou C mente e A fala a verdade.
O candidato B disse que A ou C mentem.
Opções 3: Se B mente, A fala a verdade e C fala a verdade (não bate com as opções 2, bate com as opções 1)
ou se B fala a verdade, A mente e C fala a verdade. (bate com as opções 2 e 1)

Logo por exclusão, conclui-se que B fala a verdade, A mente e C fala a verdade

Assim fica:
P = Apenas A mente (V)
Q= Apenas B mente (F)
R = A e C mentem (F)

P ^ Q = F ; Q V R = F; ~[P ^(~Q)] = F; P V R ->(P ^ Q)=F; P ^ Q<-> ~P V Q = V
Isso é obra do tinhoso...
O raciocínio do professor está correto. Mas, pra quem prefere usar uma tabela da verdade, olhem esta parte deste vídeo:
https://youtu.be/jBbUACsjOPc?list=PLNKZPo-igK8DvqyoWQ94cOu9OomL_NbXa&t=50
Pra quem não puder assistir, ele sugere que se use hipóteses e, no caso em que a maior parte de afirmativas for afirmativa, devemos assumir que esta é a verdade.
Agora, convenhamos, esta questão é pra perder tempo, muito ridícula hehe.
NAo entendi a conclusão do professor. Se A mente, então B fala a verdade. Se B fala a verdade que A mente tudo certo, mas fala que C também mente, então como o professor conclui que C fala a verdade se B dizendo a verdade diz que ele mente. Aff Professor pula etapas de raciocínio, não dá pra acompanhar se não se tem a carga de raciocínio que ele pressupõe que se tem,..
estranho o comentario do professor, pois:
se A fala a verdade, entao a proposiçao "apenas A mente" deveria ser F, e na resoluçao da letra "e" ele coloca P = V. nao entendi
resolvi assim:
O candidato A afirmou que B mente.
O candidato B disse que A ou C mentem.
O candidato C afirmou que A mente.
suponhamos que A fale mentira.
B entao fala a verdade dizendo que A ou C mentem.
por sua vez, C afirma que A mente.
P: apenas A mente. V (correto)
Q: apenas B mente. F (errado, pois sabemos que B fala a verdade)
R: A e C mentem. F (errado, pois é A ou C que mente, no caso sabemos que é A que mente.
= V^F <-> FvF = F<->F = V
Resolução de RLM deveria ser em vídeo!!!! Só acho. Vai a dica Qconcursos.
Não dá certo estudar RL as 21:10 =((((((((((((((((((((((
Não entendi nada do comentário do professor, aff que raiva desses comentário de RLM escritos, viu, apesar de que muitas vezes pelo comentários dos colegas é possível entender.
Eu posso dizer que esta eu resolvi de forma superficial, mas fui testando aquelas que eu verifiquei que estavam erradas:

Primeiro, deve ser realizado o problema e descobrir que A mente ou fala a verdadde.

Depois, verificando as alternativas a partir desse presuposto podemos inferir que A e C não podem estar mentindo simultaneamente.

Se verificarmos a C) ela está incongruente e dá um resultado do tipo "A não mente, e B diz a verdade (não podemos precisar porque é Ou, quem diz a verdade é C ou A)

e) A mente e A e B mente SE E SOMENTE SE A diz a verdade ou B mente. Logo C, diz a verdade. Não me diga...
Dica para as pessoas que também não gostam de algumas questões com as respostas digitadas pelos professores : Clica em "não gostei" na questão e fala o motivo, ou seja, as questoes de RLM devem ser respondidas em vídeo.
A explicaçao do professor e merda é a mesma coisa.
Amigos, esta é uma questão dificil. Vou tentar explicar:

A proposição P: Apenas A mente, nos leva a concluir que B e C falam a verdade.

C diz que A mente. a proposição P diz isso.

B diz que ou A ou C mentem. Como a proposição P diz, A mente, então B está dizendo a verdade.

assim val(P) = V; val(Q) = F; val(R) = F

fazendo as valorações das alternativas, ficarei com a alternativa E.) P e Q se e somente se, não P ou Q

Reparem que val(P e Q) = F e val(não P ou Q) = F. Desse modo, o se e somente se terá valor Verdadeiro. Resposta: Alternativa E
Primeiro a gente considera falar a verdade e mentir como V ou F para A, B e C. Então observamos que A e C são contraditórias. Logo B é sempre verdadeira pois ou A ou ~ A (que equivale a C), B é uma tautologia. Portanto A que é a negação de B é uma contradição, sempre falsa. Se A é falsa C é verdadeira.

P é V, pois sabemos que A é F e B e C são V.

Q é F, pois B é sempre V.

R é F, pois A e C são contraditórias e não podem ser ambas F.

Então é só calcular o valor de verdade das opções.

Alternativa e.

Pois a equivalência é verdadeira se ambos os termos são verdadeiros ou ambos falsos. Nesse caso são ambos falsos pois P e Q se somente se ~ P ou Q admite no primeiro termo que Q é verdadeira, o que é falso, e no segundo que ~ P ou Q são verdadeiras, mas são ambas falsas.
Essa é uma questão para resolver em 30 segundos:
1) A = ~B
2) C = ~A
3) B = ~A ou ~C
------------------
4) Substituindo (2) em (3), B = C ou ~C = V => B = V
5) Substituindo (4) em (1), A = ~B = ~V = F => A = F
6) Substituindo (5) em (2), C = ~A = ~F = V => C = V
Portanto, P = V, Q = F, R = F
Agora basta calcular o valor verdade de cada alternativa. A única alternativa com valor V é a letra "e".
os comentarios dos amigos deu para entender um pouco
texto

O candidato
A afirmou que B mente.
O candidato B disse que A ou C mentem.
O candidato C afirmou que A mente.
Considerando essas informações, os símbolos lógicos anteriormente mencionados e ➜ — que significa "se ..., então" — e ↔ — que significa "se, e somente se" -, e as proposições:

Resposta:
P: "Apenas A mente"; = V

Q: "Apenas B mente" e = F

R: "A e C mentem", = F

P e Q <-> ~P V Q
V e F <-> F V F
F <-> F
VERDADE
texto

Se apenas A mente (P), não tem como apenas B mentir (Q) , muito menos A e C (R), logo a bi condicional se encaixa no perfil testado.

(não sei como é com cada um, mas é questão de prática mesmo; testo só no raciocínio, sem nada de escrita a priori, depois que confirmo, valido na escrita, pois é mais rápido)

Resposta:
P: "Apenas A mente"; = V

Q: "Apenas B mente" e = F

R: "A e C mentem", = F

P e Q <-> ~P V Q
V e F <-> F V F
F <-> F
VERDADE

AVANTE..
Quem tiver um link de algum vídeo dessa resolução pf me mande

ID

149320

Banca

FCC

Órgão

TJ-SE

Ano

2009

Provas

Disciplina

Raciocínio Lógico

Assuntos

Considere as seguintes premissas:

p : Trabalhar é saudável
q : O cigarro mata.

A afirmação "Trabalhar não é saudável" ou "o cigarro mata" é FALSA se

Alternativas

p é falsa e ~q é falsa.

p é falsa e q é falsa.

p e q são verdadeiras.

p é verdadeira e q é falsa.

~p é verdadeira e q é falsa.

Comentários

Para que a afirmação "Trabalhar não é saudável" ou "o cigarro mata" seja falsa, é necessários que "Trabalhar não é saudável" seja falsa e também "o cigarro mata" seja falsa.Logo p : "Trabalhar é saudável" é verdadeira eq : "O cigarro mata" é falsa. Resposta: D
1° passo: montar a tabela verdade
P-Trabalhar não é saudável
Q-cigarro mata
P Q ~P    ~P ou Q
F F   V       V
F V   V       V
V F   F       F
V V   F      V

2° passo: comparar:
afirmação "Trabalhar não é saudável" ou "o cigarro mata" é FALSA se
Resp.: p é verdadeira e q é falsa.
Para resolver a questão é necessário montar a tabela
p     q    p v q     ~p     q     ~p v q
V      V       V          F        V           V
V     F       V         F        F           F
F      V      V         V        V           V
F      F       F         V         F          V
Para a preposição ~P v Q ser falsa, a preposição P tem que ser V e a Q tem que ser F.
Resposta letra D.

Não é preciso montar a tabela verdade!!!
Basta saber que para o conectivo OU ser falso são necessários os dois valores falsos. Se a negação de P tem que dar falso, logo, P é verdadeiro. Se Q tem que ser falso, logo, Q é falso. PRONTO!!

P = V
~P = F
Q = F
~P V Q = F V F = F
"Trabalhar não é saudável" ou "o cigarro mata" corresponde a (~p) ou (q)
para que a afirmativa seja falsa é preciso que:
(~p) = seja Falsa ------ O que implica em (p) ser verdadeira
(q) = seja Falsa

Ou seja, (p) verdadeira e (q) falsa
p : Trabalhar é saudável
q : O cigarro mata.

A afirmação "Trabalhar não é saudável" ou "o cigarro mata" é FALSA se.

Essa questão foi posta em duas etapas, na primeira as duas proposições eram verdadeiras, na segunda a primeira parte era negativa e a segunda positiva.
Mas devemos saber que ~ + ~ vira verdadeiro e positivo + ~ vira negativo.
p : Trabalhar é saudável
q : O cigarro mata.

A proposição ~p tem sempre o valor oposto de p

A Afirmação só será verdadeira na disjunção se AMBAS forem falsas

( ~p)Trabalhar não é saudável ou (q) o cigarro mata
F F = F

Por esta razão as proposições serão:

p : Trabalhar é saudável - Verdadeira

q : O cigarro mata - Falso

~p : Trabalhar não é saudavel - Falso FAFALSOf
"Trabalhar não é saudável" ou "o cigarro mata" é a frase ¬p v q.

Pela regra da correspondência temos que ¬p v q = p -> q (Se p, então q)

Pela tabela verdade do Se/Então (->) temos falso somente quando V -> F = F

P         Q       P->Q
V         F        F
V       V        V
F         V        V
F         F        V

Logo a resposta é P = V e Q = F, ou seja, p é verdadeira e q é falsa. Letra D)
Quando não temos uma resposta temos que pegar uma proposição equivalente.
Veja a proposição que foi dada:
A afirmação "Trabalhar não é saudável" ou "o cigarro mata".
Colocando em simbologia: ~ A v B
A equivalência disso é " se A então B" (A --> B)
Agora me diga, qual a única possibilidade de o "se... então" ser falso? Quando a primeira é V e a segunda é F.
Logo a resposta é a letra D.
NO CONECTIVO OU BASTA APENAS UM SER VERDADEIRO PARA QUE A SENTENÇA SEJA VERDADEIRA, ELE SÓ SERÁ FALSA QDO AS DUAS FOREM FALSAS
SENDO ~P V Q (ISTO SERÁ QUE SER FALSO) OU SEJA F F
a) P (f) ~Q (F) { V V } VERDADEIRA
B) P(F) Q (F) ....V F VERDADEIRA
C) P E Q V ...VERDADEIRA
D) P(V) Q (F)......F F (FALSA)
E) ~P (V) Q (F) ...V F ( VERDADEIRA)
Considere as premissas abaixo:

p: Trabalhar é saudável

q: O cigarro mata.

A proposição “Trabalhar não é saudável" ou "o cigarro mata" é uma disjunção:

~p v q

Assim, de acordo com a tabela–verdade, a mesma será falsa se as premissas acima forem V e F para p e q respectivamente.

RESPOSTA: (D)
p : Trabalhar é saudável
q : O cigarro mata.

"Trabalhar não é saudável" ou "o cigarro mata" é FALSA se
FALSO OU FALSO = FALSO
Trabalhar não é saudável ( é ~p) = FALSO ---> p : Trabalhar é saudável (verdadeiro)
o cigarro mata (é q) = FALSO --> q : O cigarro mata. (falso)
letra d =p é verdadeira e q é falsa.
Gente, qual a resposta ?

O site fala que é D, mas o comentário do professor é (B). Eu considero a letra b também. Segue abaixo o comentário do professor
Vinícius Werneck , Prof. de Matemática (UERJ) e Mestre em Geofísica (Observatório Nacional)
Considere as premissas abaixo:
p: Trabalhar é saudável
q: O cigarro mata.
A proposição “Trabalhar não é saudável" ou "o cigarro mata" é uma disjunção:
~p v q
Assim, de acordo com a tabela–verdade, a mesma será falsa se as premissas acima forem V e F para p e q respectivamente.
RESPOSTA: (B)
para o conectivo "ou" >>> basta uma ser verdadeira que toda a proprosição é verdadeira.logo,conclui-se que :
A) p é falsa e ~q é falsa. >>> no comando da questão o (P ) esta negado ~p ( trabalhar não é saudável então fica assim na a) foi dito que P é falso ,então ~p é verdadeiro

ERRADO: basta uma V para que toda proposição seja verdadeira , já temos um V.

B) ocorre o mesmo que aconteceu na letra A). foi dito que P é falso ,então ~p é verdadeiro
ERRADO: basta uma V para que toda proposição seja verdadeira , já temos um V.

C) p e q são verdadeiras. no comando da questão "o cigarro mata" é verdadeiro é o que se afirma na alternativa
ERRADO: basta uma V para que toda proposição seja verdadeira , já temos um V.

(A CORRETA)
D) p é verdadeira e q é falsa. se p é verdadeiro ,então a negação ~p é falso a proposição fica
(~p v q ) ---------------->>>>>>>> (f v f ) = F .
nesse caso não o correu nenhuma V para que fica-se verdadeiro .então ,é essa alternativa que permite que toda a proprosição seja falsa .
CORRETA. O QUE SE PEDE NA QUESTÃO
E) ~p é verdadeira e q é falsa. >>> no comando da questão o (P ) esta negado ~p ( trabalhar não é saudável se é verdadeira ,então .

ERRADO: basta uma V para que toda proposição seja verdadeira , já temos um V.
bOns Estudos !
Cada um resolve a sua maneira. Mas no caso basta negar toda a proposição composta e você chega à conclusão pedida na questão.
Assim:
Trabalhar não é saudável (ou) o cigarro mata.
Trabalhar é saudável (e) o cigarro não mata.
Negação da Disjunção.
Para clarear as coisas, sempre monte uma tabelinha verdade.

pVq
V
V
V
F
De acordo com o enunciado, temos: ~pVq

Vejam que a única possibilidade de a disjunção ser falsa é com F/F. Portanto, temos que colocar o V no ~p e F no q. Negando o V do ~q, temos F e assim a resposta correta é:

D) p é verdadeira e q é falsa
p: Trabalhar é saudável
q: cigarro mata
considerando p v q como uma afirmação verdadeira, então, para que ~p v q = falso teremos:
p = v então ~p = F
q = v então q = V
F v V = Falso - para que isto seja falso, precisamos que p e q sejam ambos falsos
F v F = Falso
então
1° Trabalhar é saudável (p = v)
2° Cigarro não mata (q = f)
Não consigo entender esta questão. Boiei................... já pelejei dois dias. Ai que burro...
Não se esqueça do conectivo (V)
Eu acho que a FCC errou na pergunta. Ela está perguntando que quando a afirmação será FALSA SE. Ora, se o CONECTIVO É OU, só será FALSA se ocorrer F ou F, o restante é verdadeiro,,
Concordo com o Rodrigo, se temos o conectivo OU basta uma ser verdadeira.
No caso para ser falsa com o conectivo OU as duas afirmações devem ser falsas.
Partindo da afirmação " Trabalhar não é saudável " ou " o cigarro mata " . Para esta afirmação ser falsa tanto a primeira afirmação quanto a segunda têm quer serem falsas. Logo, trabalhar é saudável e o cigarro não mata .Concluo assim que a premissa( P): trabalhar é saudável é (V), e a premissa( Q): o cigarro mata é ( F) porque o cigarro nao mata. Portanto letra d.
Veja o vídeo que gravei com a resolução dessa questão:
https://youtu.be/jtCkucgNNGM
Professor Ivan Chagas
Todo mundo, para mim, aqui explicou a mesma coisa e eu não entendi nada. Até pegar a deixa do Kratos Confidere e investigar mais a fundo.

Na explicação dele, ele dizia:

Trabalhar não é saudável (ou) o cigarro mata.

Trabalhar é saudável (e) o cigarro não mata.

Ou seja, para você negar uma conjunção existem regras. Por exemplo, para negar a disjunção inclusiva, você usa a conjunção.

P ou Q ...........................vira ......................P e Q.

Negando a afirmação dada anteriormente seguindo a regra:

"Trabalhar não é saudável" ou "o cigarro mata" = Trabalhar é saudável E O cigarro não mata.

Trabalhar não é saudável era F, virou V.

Cigarro mata era V, virou F.

Se você der uma olhada na Tabela Verdade a conjunção E.

V F F

Ou seja, um precisa ser V e outro precisa ser F, para dar F - considerando a Regrinha da Negação dita anteriormente.
Resolução comentada: http://gabaritandoeconcursos.blogspot.com.br/2016/07/raciocinio-logico-questao-resolvida-de_7.html
Considere as premissas abaixo:

p: Trabalhar é saudável

q: O cigarro mata.

A proposição “Trabalhar não é saudável" ou "o cigarro mata" é uma disjunção:

~p v q

Assim, de acordo com a tabela–verdade, a mesma será falsa se as premissas acima forem V e F para p e q respectivamente.

RESPOSTA: (D)

Fonte: QC
p: Trabalhar é saudável

q: O cigarro mata

O enunciado quer saber quando é que essa afirmação vai ser falsa: "Trabalhar não é saudável" ou " o cigarro mata" Essa afirmação pode ser representada por: ~p v q

Vamos construir a Tabela-Verdade:

p q ~p (~p v q) Então, (~pvq) vai ser falsa se p for V, q for F e ~p for falso.

V V F V Gabarito: d) p é verdadeira e q é falsa

V F F F

F V V V

F F V V
Concordo com o colega Rodrigo Talmelli. O fragmento "A afirmação "Trabalhar não é saudável" ou "o cigarro mata" é FALSA se " abre a interpretação de que a questão só quer saber a negação da proposição composta ~p v q, e não a negação da proposição equivalente a ~p v q. Apesar de eu entender a resolução da questão, talvez esta devesse ser anulada.

Quem quiser debater, pode mandar mensagem no privado.
Grato a Núbia Pattinson
Considere as seguintes premissas:

p: Trabalhar é saudável

q: O cigarro mata.

A afirmação "Trabalhar não é saudável" ou "o cigarro mata" é FALSA se

Para responder, primeiro precisamos conhecer a tabuada do “ou”, onde tudo F dá F.

Para que a afirmação acima seja falsa, portanto, será necessário que as duas proposições ligadas pelo conectivo “ou” sejam falsas.

Para que as duas proposições sejam falsas, elas devem negar/contrariar proposições tidas como verdadeiras.

Logo, para que a proposição “trabalhar não é saudável” seja falsa, é necessário que a proposição “trabalhar é saudável” seja tida como verdadeira. Logo, “p” é verdadeira e sua negação”~p”, falsa.

E para que a proposição “o cigarro mata” seja falsa na afirmação, seria necessário que a proposição “q”, escrita lá em cima, dissesse exatamente o contrário: “o cigarro não mata” e fosse tida como verdadeira(apesar de parecer loucura rs).

Assim, o gabarito é: “p” teria que ser verdadeiro e “q” teria que ser falso. Pois a afirmação negaria a proposição “p” que é verdadeira, tornando-a falsa e afirmaria “q”, tendo-a como falsa.

Assim, ambas as proposições seriam tidas como falsas NA AFIRMAÇÃO e a tabuada do “ou” se cumpriria.

Desculpem-me por ter me estendido. Se eu fosse fumante, talvez aceitasse a proposição “o cigarro mata” como falsa com mais facilidade. Nesse ponto os fumantes se deram bem. rs
~(~p v q) <-> p ^ ~q

Leis de Morgan.

Bizu = troca tudo
Obrigado Jéssica , sua explicação está melhor que a do professor!
Você contribui muito com seu comentário!
Abraços.
Sério! Não entendi!!
Boa questão

#TRT2019
https://www.youtube.com/watch?v=jtCkucgNNGM o professor descomplicou aqui
Veja que “Trabalhar não é saudável” é a negação da proposição p, isto é, ~p. Já “o cigarro mata” é a própria proposição q. Portanto, o exercício nos deu uma proposição ~p ou q.

Vimos que uma disjunção (“ou”) só é falsa se ambas as proposições que a constituem sejam falsas. Portanto, vemos que a disjunção do enunciado será falsa quando ~p for falsa e q for falsa. Entretanto, para que ~p seja falsa, o seu oposto (isto é, p) deve ser verdadeira.

Assim, “Trabalhar não é saudável ou o cigarro mata” será falsa quando p for verdadeira e q for falsa.

Resposta: D
A) Sabemos que a Questão do tipo: ~P ou Q então é só aplicar nessa Formula

A) ~F v ~F = V v V = V

B) ~F v F = V v F = V

C) ~V v V = F v V =V

D) ~V v F = F v F = F Gabarito

E) ~(~V v F) V v F = V
~(~V) Nega a primeira vez ele vira F, Depois que Negar a segunda Ele Vira V
Essa foi bem bolada porque foi apresentada a equivalente de p -> q (~p v q). Aí perguntaram: qual é a negação disso? E quem enxergou essa situação foi direto no p(V) e q(F). V -> F

Isso está na alternativa D.

ID

150910

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2008

Provas

CESGRANRIO - 2008 - BR Distribuidora - Analista de Sistemas Júnior - Engenharia de Software

Disciplina

Raciocínio Lógico

Assuntos

Se Ana sabe que Beatriz tem acesso ao sistema de almoxarifado, então Ana não fez um pedido. Ou Ana fez um pedido ou a senha de Beatriz foi descoberta. Se Carlos conversou com Ana, então Ana sabe que Beatriz tem acesso ao sistema de almoxarifado. Ora, nem a senha de Beatriz foi descoberta nem Beatriz conhece Carlos. Logo:

I - Ana fez um pedido;

II - Ana sabe que Beatriz tem acesso ao sistema de almoxarifado;

III - Carlos não conversou com Ana;

IV - Beatriz conhece Carlos.

São verdadeiras APENAS as conclusões

Alternativas

I e II

I e III

II e III

II e IV

III e IV

Comentários

Basta testar as alternativas ou prestar atenção na ultima frase:
I verdade (ela não descobriu a senha)
II mentira (então Ana não fez um pedido)
III verdade (se Ana não sabe de Beatriz ela não falou com Carlos)
IV mentira (a frase nega as duas opções)
P: Ana sabe que beatriz tem acesso ao sistema de almoxarifado
Q: Ana fez pedido
R: A senha de Beatriz foi descoberta
S: Carlos conversou com Ana
T: Beatriz conhece Carlos

"nem a senha de Beatriz foi descoberta nem Beatriz conhece Carlos"

Logo,
R é Falso
T é Falso

Agora rescrevendo o enunciado da questão usando quantificadores lógicos:

P -> ~Q :V
Q v R :V
S -> P :V

Resolvendo,
para QvR, lembrando que R é Falso, Q deverá ser Verdadeiro para termos resultado Verdadeiro.

P->~Q, sabendo agora que Q é Falso, só terá como resultado Verdadeiro quando P for Falso

S->P só terá resultado verdadeiro (quando P for falso) quando S for Falso.

Portanto,
P é Falso
Q é Verdadeiro
S é Falso
R e T são Falsos
Para resolver esta questão basta organizar as proposições e usar a penúltima declaração (A senha de BEATRIZ NÃO foi descoberta). A última declaração não tem nada haver com as proposições~~(Beatriz não conhece Carlos)~~

Obs: Cada declaração tem que ter o valor VERDADE seguindo as tabelas verdades das operações(&, OR, XOR, SE ENTÃO, SE SOMENTE SE)
Começando com a proposição 2:
   (VERDADE)                               (FALSO)
2 - Ou Ana fez um pedido OU a senha de Beatriz foi descoberta.
Obs: A primeira proposição deve ser VERDADE para a sentença ser verdadeira.
Logo a Ana fez um pedido. VERDADE OU FALSO = VERDADE

1 - Se Ana sabe que Beatriz tem acesso ao sistema de almoxarifado, (FALSO)
           então Ana não fez um pedido. (FALSO) pois Ana FEZ o pedido
obs: Para que este proposição seja verdade, é preciso ter um FALSO na declaração SE.
Logo, Ana NÃO sabe que Beatriz tem Acesso ao sistema. Se fosse verdade, ficaria:
SE VERDADE Então FALSO = FALSO.
Como eu falei, o resultado das proposições devem ser VERDADE.

                       (FALSO)
3 - Se Carlos conversou com Ana,
então Ana sabe que Beatriz tem acesso ao sistema de almoxarifado. (FALSO)
Obs: Para que esta proposição seja verdadeira, a declaração do SE deve ser FALSA
para que tenhamos SE FALSO ENTÃO FALSO = VERDADE.

Logo:
Ana fez um pedido;
Carlos não conversou com Ana;
I e III

Segue as tabelas utilizadas:
Uma vez que: A SENHA DE BEATRIZ NÃO FOI DESCOBERTA, logo I - ANA FEZ UM PEDIDO (OU ANA FEZ UM PEDIDO OU ~~A SENHA DE BEATRIZ FOI DESCOBERTA~~), se ANA FEZ UM PEDIDO, logo ANA NÃO SABE QUE BEATRIZ TEM ACESSO AO SISTEMA (~~Se Ana sabe que Beatriz tem acesso ao sistema de almoxarifado~~, então Ana não fez um pedido. ANA FEZ UM PEDIDO) , até aqui eliminamos a II:

~~II - Ana sabe que Beatriz tem acesso ao sistema de almoxarifado;~~

ANA NÃO SABE QUE BEATRIZ TEM ACESSO AO SISTEMA (~~Se Carlos conversou com Ana~~, então Ana sabe que Beatriz tem acesso ao sistema de almoxarifado.), logo III - CARLOS NÃO CONVERSOU COM ANA

E por último nem NEM BEATRIZ CONHECE CARLOS, logo eliminamos a ~~IV - BEATRIZ CONHECE CARLOS~~

I - ANA FEZ UM PEDIDO - CORRETO
III - CARLOS NÃO CONVERSOU COM ANA - CORRETO

Vamos lá.

1) Vamos lembrar das tabelas verdades

A	B	SE -> ENTÃO	E	OU
V	V	V	V	V
V	F	F	F	V
F	V	V	F	V
F	F	V	F	F

2)
    2.1) Se Ana sabe que Beatriz tem acesso ao sistema de almoxarifado, então Ana não fez um pedido.
    2.2) Ou Ana fez um pedido ou a senha de Beatriz foi descoberta.
    2.3) Se Carlos conversou com Ana, então Ana sabe que Beatriz tem acesso ao sistema de almoxarifado.

3) Vamos associar os argumentos, fornecidos no enunciados, a letras.

P: Ana sabe que beatriz tem acesso ao sistema de almoxarifado = F
Q: Ana fez pedido = V
R: A senha de Beatriz foi descoberta = F
S: Carlos conversou com Ana
T: Beatriz conhece Carlos = F

4) Começando a análise:

    a) Ora, nem a senha de Beatriz foi descoberta nem Beatriz conhece Carlos; Logo, concluímos que tanto a letra R quanto a letra T são falsas.

    b) Partindo para a análise do item 2.2 temos:
---> Ou Ana fez um pedido ou a senha de Beatriz foi descoberta (Q ou R).
---> Para a assertiva ser tida como verdade teremos que ter Q como Verdadeiro, pois o R já é falso ( A senha de Ana não foi descoberta ). V ou F = V

    c) Partindo para a Análise do item 2.1 temos:
---> Se Ana sabe que Beatriz tem acesso ao sistema de almoxarifado, então Ana não fez um pedido ( P -> ñ Q ).
---> Para a assertiva ser tida como verdade teremos que ter P como falso, pois __ -> F = V (basta olhar a tabela verdade e verificar que a única possibilidade é P ser falso).

d) fazendo a mesma coisa para o item 2.3 obteremos como resposta que S tem de ser Falso.

### Após isso vamos para os itens a serem avaliados ####

I - Ana fez um pedido; = V

II - Ana sabe que Beatriz tem acesso ao sistema de almoxarifado; = F

III - Carlos não conversou com Ana; = V

IV - Beatriz conhece Carlos. = F

ID

152407

Banca

CESPE / CEBRASPE

Órgão

TRE-MG

Ano

2009

Provas

Disciplina

Raciocínio Lógico

Assuntos

Proposições são sentenças que podem ser julgadas somente como verdadeiras ou falsas. A esse respeito, considere que p represente a proposição simples "É dever do servidor promover o atendimento cordial a clientes internos e externos", que q represente a proposição simples "O servidor deverá instruir procedimentos administrativos de suporte gerencial" e que r represente a proposição simples "É tarefa do servidor propor alternativas e promover ações para o alcance dos objetivos da organização". Acerca dessas proposições p, q e r e das regras inerentes ao raciocínio lógico, assinale a opção correta.

Alternativas

é equivalente a Imagem 006.jpg

é equivalente a Imagem 008.jpg

é equivalente a Imagem 010.jpg

A tabela-verdade completa das proposições simples p,q,r tem 2⁴ linhas.

Comentários

b) ~q -> ~p

c) p _^ (q v r) é equivalente a (p _^q) v ( p _^r)

d) ~(~(~r)) = ~r , logo ~r <->r é Falso.

e) A tebela-verdade tem 2³ linhas (pois são 3 proposições)

:)

Como calcular o número de linhas
Número de linhas
2? =
Número de valorações

a) 2? = 2¹ = 2
p

b) 2? = 2² = 4
p ^ q

p	q
V	V
V	F
F	V
F	V

c) 2? = 2² = 4
(p ^ q) condicional q

p	q
V	V
V	F
F	V
F	V

d) d) 2? = 2³ = 8
(p ^ q) condicional r

p	q	r
V	V	V
V	V	F
V	F	V
V	F	F
F	V	V
F	V	F
F	F	V
F	V	F

Resumo da tabela verdade com os conectores “e” ^ “ou” v “condicional” e “bicondicional”

p ^ q

p condicional q

p bicondicional q

p v q

alternativa A.
pois parte do conceito de Leis de Morgan:
exemplo 1: equivalência a ~p ^ ~q ^ ~r.
exemplo 2: ~( p ^ q ^ r ) eqquivalência a ~p v ~q v ~r.
A (a) está correta, isso eu concordo, porem o que está erado na (d)? Ao preencher suas linhas achei todas as oito (F), mais notem que esta questão, ao meu ver, poderia ser anulada. A (d) NÃO estabelece parâmetros para o aluno resolver entre certo ou errado.
Ou seja, faltou algo nesta acertiva.
Pheliphe, nas sucessivas negações, basta você ir anulando uma negação com outra.
Ex: Se há duas negações( ~ ~) estas duas se anularam e o que vier após elas será a verdade.
Veja como fica em uma frase:
Não vou à praia, não! Estes dois "nãos" se anulam e o que a frase quer dizer é, na verdade: Vou à praia.

Agora vejamos a letra D da nossa questão:

~(~(~r) ) se e somente se r.
Veja que podemos anular uma negação com a outra e sobrará
~r se e somente se r. De modo que independente do valor de r, a questão será falsa, pois no momento em que um dos "r" for verdadeiro o outro "~r"será falso, e sabemos que para que a questão fosse verdadeira, ambos os valores de "r" teriam que ser verdadeiros ou ambos teriam que ser falsos.
Paulo Sampaio....na "E" você disse que há 23 linhas, como isso? você está enganado, pois 2³ = 8, ou seja, 8 linhas.

Bons Estudos!!!
a)~(p\/q\/r) é equivalente a ~p^~q^~r de acordo com a regra de equivalencia. Quando há negação (~) na frente da expressão, alteram-se todos os valores assim com o operador. Logo, \/ torna-se ^, e o oposto. Na tabela da verdade, ficam todos resultados F, com exceção da ultima linha: V.
LEI DE De Morgan

A B ¬A ¬B A ∧ B ¬ (A ∧ B) ¬A ∨ ¬B
V V F F V F F
V F F V F V V
F V V F F V V
F F V V F V V

ambas negação de A ∧ B
pra não zerar?
CESPE é você?

ID

279451

Banca

CONSULPLAN

Órgão

Prefeitura de Itabaiana - SE

Ano

2010

Provas

Disciplina

Raciocínio Lógico

Assuntos

Sejam os conjuntos: A = { x ∈ N / 1 ≤ x < 5 }; B = { x ≤ Z /-3 < x ≤ 4 } e C = { x ∈ N / x ≤ 3 } Pode-se concluir que:

Alternativas

(A ∪ B ) ∩ (B ∪ c) = A ∩ C

( A ∩ C ) ∪ ( B ∩ C ) = C ∩ B

( A ∩ B ) ∪ ( B ∩ C ) = A ∪ C

( A ∪ C ) ∩ ( B ∩ C ) = B ∩ C

(A ∩ B ) ∩ ( B ∩ C ) = A ∩ B

Comentários

Na questão A= {xeN/ 1<= x <5} ou seja = x pertence a numeros naturais tal que 1 menor igual a x que é menor que 5, assim 1,2,3,4;
Na questão B= {xeZ/ -3 x <=4} ou seja = x pertence a numeros inteiros tal que menos 3 x menor igual a 4, assim -2,-1,0,1,2,3-4;
Na questão C= {xeN/ x<= 3} ou seja = x pertence a numeros naturais tal x menor igual a 3, assim 0,1,2,3,;

Analisando as questões temos a letra C: (A intersecção com B) União (B intersecção C) = A União com B

A intersecção com B = 1,2,3,4
B Intersecção com C = 0,1,2,3
A União dos dois resulta em 0,1,2,3,4
que é igual a
A U C = 0,1,2,3,4

Abraços
Fazendo a montagem dos conjuntos:
A={0,1,2,3,4}
B={-2,-1,0,1,2,3,4}
C={0,1,2,3}

Fazendo primeiramente a união:
AUB=>B ---- A={0,1,2,3,4} U B= {-2,-1,0,1,2,3,4} => B={-2,-1,0,1,2,3,4}
AUC=>A ---- A={0,1,2,3,4} U C={0,1,2,3} => A={0,1,2,3,4}
BUC=>B --- B={-2,-1,0,1,2,3,4} U C={0,1,2,3} => B={-2,-1,0,1,2,3,4}

A interseção:

A e B=> A   A={0,1,2,3,4} e B=~~{-2~~,-1,0,1,2,3,4} =>   A={0,1,2,3,4}
A e C => C A={0,1,2,3,4} e C={0,1,2,3} =>  C={0,1,2,3}
B e C => C B={-2,-1,0,1,2,3,4} e C={0,1,2,3} =>  C={0,1,2,3}

* desculpem-me o uso do "e"

Fazendo as resoluções das questôes:

a) (A U B) e (B U C)= B e B, então A e C está errado
b) (A e C) U ( B e C) = C U C, então C U B está errado
c) (A e B) U ( B e C) = A U C, então a alternativa está correta
d) (A U C) e (B U C) = A e B, então B e C está errado
e) (A e B) e ( B e C) = A e C, então A e B está errado

Logo, a alternativa correta é a letra c)
Naturais se restringe aos positivos!!
Shyrleide Martins, seu raciocínio está correto, mas atente para o fato de que o conjunto A= { 1, 2, 3, 4}, visto que no enunciado da questão é informado que 1 é menor ou igual a x, então o conjunto A não contém 0.
Questão fácil, porém trabalhosa.
Nossa Senhora, que sono essa professora comentando a questao kkkk Desisto
questao completamente desgraçada. Pra que o infeliz do avaliador faz uma coisa assim? É um infeliz!
{XEN/1<=X<5}= Se X é maior ou igual a 01, o Zero entra no conjunto?
Trabalhosa, mas não impossível! UFFA!
Deu trabalho, mas valeu a pena.

GABARITO "C"
Cuidado. Não pode ter 0 no conjunto A, tal como informado pela Shyrleide Martins.

ID

282700

Banca

FGV

Órgão

CODESP-SP

Ano

2010

Provas

FGV - 2010 - CODESP-SP - Técnico em Agrimensura - Tipo 1

Disciplina

Raciocínio Lógico

Assuntos

André, Bruno, Carlos e Maria estão em uma festa num grande salão retangular ABCD, de dimensões AB=6m e BC=8m. André, Bruno e Carlos estão, respectivamente, nos vértices A, B e C do salão, enquanto Maria está exatamente no centro do salão. Em determinado momento, André, Bruno e Carlos caminham em linha reta até Maria. Sendo a, b e c as distâncias percorridas, respectivamente, por André, Bruno e Carlos, tem-se que

Alternativas

a<b<c

a=c<b

a=b<c

b=c<a

a=b=c

Comentários

Gab: E
As diagonais de um quadrado ou de um retângulo são iguais, ou seja, independente de partir de algum vértice, a distância até o centro será a mesma.
D = SQRT( B^2 + H^2)

Caso queira saber porque essa equação surgiu, imagine um retângulo e corte ele ao meio, dividindo em 2 triângulos retângulos, já que é inviável eu desenhá-lo aqui (eu tentei, mas não saiu do jeito esperado)
Uma das maneiras de se encontrar a diagonal é calcular a hipotenusa do triângulo retângulo inferior ou superior.

Diremos que a largura é L(parte de baixo) e a altura, H (parte vertical), ou seja, AB = largura e BC = altura (sim, pode ser o contrário, não tem problema)

D^2 = L^2 + H^2 , em que D é diagonal

D = SQRT(L^2 + H^2) SQRT == raiz

como só iremos pegar metade da diagonal

X = 1/2 * SQRT(L^2 + H^2) ou D/2 = 1/2 *SQRT(l^2 + H^2)

X = 5m (8^2 +6^2) = 100; SQRT(100)= 10; 10/2 = 5

P.S.: Obviamente, não precisava fazer o cálculo, basta saber que as diagonais possuem as mesmas distâncias, entretanto, decidi deixar aqui para fins lúdicos, àqueles que não saibam essa informação
Tendi foi nada..
DESENHEI UM RETÂNGULO COMO CITA A QUESTÃO E COLOQUEI AS VÉRTICES AB E BC APÓS ISSO COLOQUEI ANDRÉ NO A, BRUNO NO B E CARLOS NO C. MARIA NO MEIO DO RETÂNGULO E OS TRÊS VÃO CAMINHAR ATÉ MARIA QUE ESTÁ NO CENTRO OU SEJA OS TRÊS VÃO CAMINHAR A MESMA DISTÂNCIA.
A=B=C.
GABARITO E
PMCE 2021!!
O 6m é só para encher linguiça, a distância principal é os 8m, como Maria foi para o meio, o retângulo "foi cortado ao meio", como A,B,C estavam no vértice, os três caminharam a mesma distância, 4m.
Traça-se uma semi reta a partir do meio da largura 6m, paralela ao comprimento de 8m até atingir ao ponto Médio que é M. Vai dar 4 m.

Traça-se a diagonal de A ou B até M, formando um triângulo retângulo.

Usa-se Pitágoras

x²=(8/2)² + (6/2)²
x² = 4² + 3²
x² = 16 + 9
x² = 25
x = V25
x = 5, sendo x a distância de A ou B ou C até M

comprova-se A=B=C

#RUMOAPMCE
OS 3 VÃO PERCORRER EXATAMENTE 5 METROS ATÉ CHEGAR A MARIA
OS 3 VÃO PERCORRER EXATAMENTE 5 METROS ATÉ CHEGAR A MARIA
OS 3 VÃO PERCORRER EXATAMENTE 5 METROS ATÉ CHEGAR A MARIA
Triângulo notável 3,4 e 5!

ID

282706

Banca

FGV

Órgão

CODESP-SP

Ano

2010

Provas

FGV - 2010 - CODESP-SP - Técnico em Agrimensura - Tipo 1

Disciplina

Raciocínio Lógico

Assuntos

Se x é A, então y é B. Se y não é B, então z é C. Sabe-se que z não é C. Logo, tem-se obrigatoriamente que

Alternativas

x é A.

x não é A.

y é B.

y não é B.

z é C.

Comentários

Se x é A (?), então y é B (V) =V
Se y não é B (F), então z é C (F) =V
Sabe-se que z não é C.

Logo, tem-se obrigatoriamente que (Y é B)
GAB. C

-Se X é A (Não tem como afirmar), então Y é B (V) = F ou V
-Se ~Y é B (F), então Z é C (F) = V

-~Z é C
Gaba. C

De trás para frente: Afirmou-se que Z não é C, então esta é verdadeira.
Ele depois diz: Se Y não é B, então Z é C, mas Z NÃO é C, então o Y é B.
Finalmente: Se X é A, então Y é B, bom, Y é B então o X pode ser A ou não, isso não torna esta condição obrigatória.
fiz assim:
X=A
Y=B
Y ~ (NN FOR) B: Z É C
SE Z NN É C: Y VAI SER B.
X=A -> Y=B (V)

~Y=B -> Z=C (V)

~Z=C (V)

Quando a questão não informar nada, deverá ser considerado que todas as proposições são verdadeiras, sendo assim:

Se Z não é igual a C, ou seja, "Z=C"(F), e na condicional, não se admite o Vera Fischer (V e F), "~Y=B" obrigatoriamente será falso.

Se "~Y=B" é falso, "Y=B" é verdadeiro, podendo o "X=A" ser verdadeiro ou falso, eliminando as alternativas "a" e "b", já que não é possível valorá-la, e deixando claro que não pode ser a letra "d", já que "Y=B"

Além disso, a própria questão afirma que o Z não é igual ao C, eliminando assim a letra "e".

Gabarito: Letra C.
Resumindo, pega-se de trás para frente.

Z ñ C (v)

se Y ñ B (f), então Z é C (f)

se X é A (f), então Y é B (v)

logo Y é B, item C

#RUMOAPMCE
Como eu resolvi essa questão:
peguei as sentenças e transformei na equivalência do "ou"
Logo ficou assim:
Premissa 1 -> X não é A ou Y é B
Premissa 2 -> Y é B ou Z é C
premissa 3 -> Z não é C
Como Z não é C e, na premissa 2 fala que, ou Y é B ou Z é C, então só corto o Z é C
da premissa 2 e tenho o Gab Y é B

Essa foi a maneira mais rápida que me fez chegar no resultado, não é a melhor, mas acredito que seja simples, quando uso a tabela me confundo e nunca
chego no resultado. Qualquer equívoco meu dar um salve que é noix haha
Xa ---> Yb ~Yb ---> Zc se Zc é falso, ~Yb só pode ser falso, pq VF na condicional é Falso. voltamos assim pra primeira sentença, que Yb é verdadeiro. não podemos dizer se Xa é F ou V, pois na condicional ambos podem ser verdadeiros. portanto, gabarito letra C. Y é B

ID

313135

Banca

CESPE / CEBRASPE

Órgão

TJ-ES

Ano

2011

Provas

CESPE - 2011 - TJ-ES - Cargos de Nível Superior - Conhecimentos Básicos (somente para os cargos 3, 4, 5 e 17)

Disciplina

Raciocínio Lógico

Assuntos

Considerando as proposições simples p e q e a proposição composta S:[ (p→q) ∧ (~q) ]→(~p), julgue os itens que se seguem.

Considerando todos os possíveis valores lógicos das proposições p e q, é correto afirmar que a proposição (p→q) ∧ (~q) possui valores lógicos V e F em quantidades iguais.

Alternativas

Certo

Errado

Comentários

Se fiz corretamente...

p   q      (p→q) ∧ (~q)

V   V      V ∧   F   = F
V   F    F ∧   V   = F
F   V      V ∧   F   = F
F   F      V ∧ V = V

"Si vis pacem parabellum"
Errado. Montando a tabela verdade toda:

p         q        (p->q)         ~q        ~p        (p->q) ^ (~q)       [(p -> q) ^(~q) -> (~p)
v           v               v                 f              f                     f                                     v
v           f                f                 v              f                     f                                     v
f            v               v                 f              v                    f                                     v
f            f                v                 v             v                    v                                     v
A proposição composta S é uma tautologia, possui valos verdadeiro para todas as combinações dos valores lógicos de suas proposições simples.
e só fazer o teste lógico
nA(V) > B(V)=V B=V,POIS NO ENTÃO V COM F = F
nA=V
CONCLUSÃO B=V
CONSIDERE AS PREMISSAS VERDADEIRAS
É simples: a questão remete ao conectivo e que possue só um valor lógico V e três F.
(p→q) ∧ (~q)

Conectivo "^" só aceita duas verdades para ser verdadeiro, então nada de quantidade igual, 1v e 3f.

Estude e confie!
QUESTÃO ERRADA
Não precisa perder tempo montando a tabela verdade, vejamos:
vamos substituir (p --> q) por "X" e (~ q) por "Y", logo:
X ^ Y só é verdadeiro quando os dois elementos são verdadeiros (V ^ V), nas outras 3 opções (V ^ F), (F ^ V) e (F ^ F) é falso.
concluindo: 1V e 3F
S:[ (p→q) ∧ (~q) ]→(~p) = TAUTOLOGIA (VVVV)

(p→q) ∧ (~q): = (FFFV)

GABARITO ERRADO
Errado.

Questão simples, pessoal vendo pelo no rabo do tatu .ha ha ha

Valores lógicos das proposições :

P= v
Q=v
¬Q=f

Logo, a proposição (p→q) ∧ (~q) possui 2 valores lógicos V e 1 valor F .
O resultado deu FFFV, porém em toda tabela verdade há seis F/V cada... acho que a pegadinha está aí.

ID

344896

Banca

MOVENS

Órgão

Prefeitura de Manaus - AM

Ano

2010

Provas

Disciplina

Raciocínio Lógico

Assuntos

A sentença “Hoje não nevou, então Lucas não foi patinar e Gustavo não foi à escola” é corretamente representada por

Alternativas

~ p ∨ ( ~ r ∧ ~ q )

~ p ∧ ( ~ r ∨ ~ q )

~ p → ( ~ r ∧ ~ q )

p → ( ~ r ∧ ~ q )

Comentários

c-

conjunção - E

nao - ~

ID

361057

Banca

MOVENS

Órgão

Prefeitura de Manaus - AM

Ano

2010

Provas

MOVENS - 2010 - Prefeitura de Manaus - AM - Técnico - Assistente Administrativo - Tipo a

Disciplina

Raciocínio Lógico

Assuntos

A sentença “Hoje não tem luar, então Sandra não foi ao trabalho e Lúcia não foi à Igreja.” pode ser corretamente representada por:

Alternativas

~ p ∨ ( ~ r ∧ ~ q )

~ p ∨ ( ~ r ∧ ~ q)

~ p → ( ~ r ∧ ~ q )

p → ( ~ r ∧ ~ q )

Comentários

Gabarito C.

O se..então é representando por ''-->'', então eliminamos A e B. Agora bastava adicionar o sinal de negação (~) antes de cada proposição, conforme a alternativa C.

ID

494926

Banca

CESPE / CEBRASPE

Órgão

CGE-PB

Ano

2008

Provas

CESPE - 2008 - CGE-PB - Auditor de Contas Públicas

Disciplina

Raciocínio Lógico

Assuntos

A controladoria geral (CG) de determinado estado realizou e concluiu, em 2007, 11 auditorias operacionais e 42 inspeções; emitiu 217 pareceres técnicos, sendo 74 referentes a licitações de obras, 68 referentes a análises de prestação de contas, 71 referentes a análises de rescisão de contrato de trabalho; o restante desses pareceres referiam se a orientações e outros assuntos.

Proposições são sentenças que podem ser julgadas como verdadeiras — V — ou falsas — F —, mas não como ambas. Considerando que todas as proposições contidas no texto acima são verdadeiras e supondo também que a proposição “Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções” seja verdadeira, assinale a opção que, por conseqüência dessas premissas, é uma proposição verdadeira.

Alternativas

Se foi produzido relatório final, então foram realizadas e concluídas 42 inspeções.

Foi produzido relatório final.

Foram realizadas e concluídas mais de 42 inspeções.

Foi produzido relatório final se e somente se foram realizadas e concluídas 42 inspeções.

Não foram realizadas nem concluídas 42 inspeções, mas foi produzido relatório final.

Comentários

Não entendi essa... Alguém pode me explicar?
Acho que o raciocínio era este: “Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções” , então como em 2007 o Estado realizou e concluiu 42 inspeções, logo foi produzido relatório final.
A única situação em que uma proposição p >> q é falsa é quando p = V e q = F
Vamos a frase: Se (não foi produzido relatório final) então ( não foram realizadas e concluídas 42 inspeções). Frase com valor lógico verdadeiro. Ou seja, ela não tem essa combinação acima.
Ela poderá ser: Se V então V; Se F então V ;Se F então F >> Possibilidades que a deixam com valor lógico verdadeiro. Até aí tudo bem?
Vamos lá! Temos que saber qual dessas 3 combinações se refere a esta frase antes de irmos para as alternativas.
No enunciado ele considerou que tudo o que está dizendo nesse texto é verdadeiro:
A controladoria geral (CG) de determinado estado realizou e concluiu, em 2007, 11 auditorias operacionais e 42 inspeções; emitiu 217 pareceres técnicos, sendo 74 referentes a licitações de obras, 68 referentes a análises de prestação de contas, 71 referentes a análises de rescisão de contrato de trabalho; o restante desses pareceres referiam se a orientações e outros assuntos.
Ora, se tudo o que está nesse texto é verdadeiro, vamos pegar a informação que nos interessa: concluiu 42 inspeções
Se essa informação é verdadeira, concordam que a informação não concluiu 42 inspeções é falsa?
Já sabemos que não concluiu 42 inspeções é falsa. Sabemos se não concluiu o relatório é falso ou verdadeiro? Com certeza! Como?
Vamos lá! Lembram que eu disse no inicio que a combinação para uma proposição Se, então só será falsa quando a primeira for verdadeira e a segunda for falsa?
Pois é! Sabendo que a segunda é falsa a primeira não pode ser verdadeira porque o enunciado disse que a proposição: "Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções” é verdadeira. Para isso a frase "não foi produzido relatório final" é falsa. Ou seja essa proposição é Se F então F = V.
Invertendo as duas frases para verdades tempos as seguintes frases:
I - Foi produzido relatório final
II - Foram realizadas e concluídas 42 inspenções
Analisando as alternativas chegamos a primeira frase. Alternativa B
Fazendo a Tabela - Verdade para a proposição “Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções", afim de sabermos a valoração de cada premissa contida nela, e sabendo que a mesma também é verdadeira, temos:

Obs.: “Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções", pode ser reescrita como: A→B.

Logo, de acordo com a tabela-verdade, a proposição A é garantidamente F, pois no caso em que a mesma aparece como V, a proposição A→B pode ser F ou V. Assim se A é falsa, então ~ A é:

Foi produzido relatório final.
Resposta: Alternativa B.
negação dupla resulta em uma afirmação.
Perfeita sua explicação Willian Silva!!! Obrigada.
Com a explicação ficou mais fácil de entender
Não entendi o ~ A ?? Alguém pode me ajudar please !
Willian Silva, por quê o lance de converter as expressões para verdadeiras no final ? Não entendi.
Cleber, normalmente o raciocínio lógico trabalha com as informações verdadeiras. Descobrimos as informações falsas. Para saber quais são as verdadeiras , invertemos.
O enunciado diz: ''Considerando que todas as proposições contidas no texto acima são verdadeiras''

A: Se foi produzido relatório final,

B: então foram realizadas e concluídas 42 inspeções

P1: A --> B = VERDADEIRA
V --> V = VERDADEIRA

P2: ~A --> ~B = VERDADEIRA
F --> F = VERDADEIRA

C: A = VERDADEIRA

GABARITO ''B''
Galera, pra quem boiou com as explicações dadas aqui nos comentários e com a do professor, vou tentar simplificar.

O próprio enunciado diz que as informações contidas nele são verdadeiras. Também nos dá uma proposição "Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções" que vamos convenientemente chamar de ¬A --> ¬ B

Aí que tá o pulo do gato pra questão toda! Lendo o texto, sabemos que foram realizadas e concluídas 42 inspeções, logo ¬B = F!
A nossa condicional está assim ¬A --> F. O enunciado nos disse que ela também é verdadeira! Então ¬A tem que ser F, logo ¬A = F.

Fiquei matutando aqui o porquê de a alternativa A) não ser considerada correta, eis o motivo: "Se foi produzido o relatório então foram realizadas e concluídas 42 inspeções" pode ser escrita assim: A -- > B, que também seria verdadeira, porquê deduzimos os valores das proposições, mas ela não foi considerada a correta, pelo simples fato que você não precisaria deduzir coisa alguma, sabendo que B = V (tá no texto, logo, de acordo com o enunciado é verdade) a proposição seria verdadeira INDEPENDENTEMENTE de você saber o valor de A!

Já na alternativa B), você necessariamente teria que saber o valor de A para respondê-la, ela é "a mais correta".
Obrigado Paulo Melo.

Temos a proposição : “Se não foi produzido relatório final, então não foram realizadas e concluídas 42 inspeções”

P= ñ foi produzido relatório final
Q= ñ foram realizados 42 inspeções
R= ñ foram concluídos 42 inspeções

p->(q^r) = V (proposição é verdadeira, conforme o texto)

p=?
q e r = f (A controladoria geral (CG) de determinado estado realizou e concluiu, (...) 42 inspeções; conforme o enunciado do texto realizou-se e concluíram-se 42 inspeções, logo q e r são falsas na proposição)

p-> (f^f)(conjunção com termo falso é f)=V
p->f=v

Então para que a proposição seja verdadeira, "p" tem que ser falso, por causa da condicional.

f->f = V

Continuando, por que a alternativa "A" está incorreta? porque no restante do enunciado temos:
"assinale a opção que, por conseqüência dessas premissas, é uma proposição verdadeira.

Nós só descobrimos o valor de "p" por causa do valor das premissas "q" e "r"!

Já "q" e "r", nós descobrimos por causa do enunciado.

Então já que o P= não foi produzido relatório final e P é falso, logo é Verdade que "Foi produzido relatório final".

Gabarito: B
A e B CORRETAS
Essa é genial!
A proposição é escrita como A→B
a proposição A é garantidamente F, pois no caso em que a mesma aparece como V, a proposição A→B pode ser F ou V. Assim se A é falsa, então ~ A é:
Meu DEUS quanto blá blá blá..... nesses comentários.

É simples.

O conectivo (Se---> então) quando o termo PRECEDENTE for (F)also, a sentença SEMPRE será verdadeira e ponto final.

Gabarito letra (B)

Bons estudos.

ID

547180

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Técnico de Projetos, Construção e Montagem Júnior - Elétrica

Disciplina

Raciocínio Lógico

Assuntos

Em uma sacola existem três bolas: uma grande (G), uma média (M) e uma pequena (P). Uma delas é azul, outra é vermelha e a terceira é amarela. Sabe-se que

• a bola G ou a bola P é de cor azul.
• a bola G é vermelha ou a bola M é amarela.
• a bola M ou a bola P é de cor amarela.
• a bola M ou a bola P é de cor vermelha.

Considerando que, nesse contexto, usa-se o ou excludente, as cores das bolas G, M e P são, respectivamente,

Alternativas

vermelha, amarela e azul.

azul, amarela e vermelha.

azul, vermelha e amarela.

amarela, vermelha e azul.

amarela, azul e vermelha.

Comentários

''Considerando que, nesse contexto, usa-se o 'OU' excludente'' = Disjunção exclusiva (OU... OU...).

Então temos:

ou G ou P de cor Azul;

ou G de cor Vermelha, ou P de cor Amarela;

ou M ou P de cor Amarela;

ou M ou P de cor Vermelha.

Se P pode ser Amarela ou Vermelha, então ''P de cor Azul'' é Falso e G é Azul. ''G de cor Vermelha, ou P de cor Amarela'' também são falsas, logo P é Vermelha e M é Amarela.

Gabarito: C.
Nesse tipo de questão, o ideal é fazer uma tabela e colocar na vertical as cores e horizontal os tamanhos e chutar uma cor para cada tamanho, depois vai desenrolando a questão lembrando que OU é exclusão Ou...Ou
Ex: Chutei que o G era azul e deu certo de primeira, mas nem sempre é assim!

ID

599380

Banca

CESPE / CEBRASPE

Órgão

EBC

Ano

2011

Provas

CESPE - 2011 - EBC - Cargos de Nível Superior - Conhecimentos Básicos - Cargo 4 Advocacia

Disciplina

Raciocínio Lógico

Assuntos

Considerando as proposições simples P e Q e a proposição composta R simbolizada por ( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q ), julgue os itens subsequentes.

Se P tem valor lógico F, então, independentemente de Q ser V ou F, R será sempre F.

Alternativas

Certo

Errado

Comentários

O texto do enunciado possui um erro de grafia e será corrigido em breve. Entretanto se olharmos na prova original:
(PVQ) ^ ~P -> (P^Q)v~Q

Tabela verdade de "Se, então" (->) só é falsa em: V -> F
Tabela verdade de "e" (^) será falsa se uma das variáveis também for falsa.
Tabela verdade de "ou" (v) será falsa somente quando as duas variáveis forem falsas.

Desta forma, se olharmos apenas para (P^Q)v~Q veremos que para ser falso dependerá diretamente de que Q seja VERDADE.

Resposta = ERRADO
A questão nos dá P: F

R = (PvQ)^(~P) --> (P^Q)v(~Q) ,

(PvQ)^(~P) --> (P^Q)v(~Q):F somente se (PvQ)^(~P):V e (PvQ)v(~Q):F

(PvQ)^(~P):V quando PvQ:V e somente quando Q:V essa preposição será verdadeira!

Se Q fosse falso, ficaria assim: (PvQ)^(~P) = (VvF)^V = V^V = V

Item errado

Boa Sorte!
Resolvi assim:

se o conectivo da primeira parte da proposição R é o "e", para que essa primeira parte seja VERDADE é preciso ser "verdade e verdade", se P tem valor lógico verdadeiro, o ~P tem que ser obrigatoriamente falso, o que torna falsa a primeira parte da proposição composta R.

se for falsa a primeira parte de uma proposição composta cujo conectivo é o "se... então", NUNCA ELA PODERÁ SER FALSA, será sempre verdadeira.

bons estudos a todos....
Amigos e colegas,

eu estou encontrando uma grande dificuldade de estudar lógica.

Alguém tem algum macete?

Não consigo inserir as alterações das afirmações nos exercícios.

Eu agradeço

bons estudos a todos
A quertão está errada!
Fiz assim:
R: ( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )

Se P é F e Q é V então R será F
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
FvV ^ V -> F^V v F
V ^ V -> F v F
V -> F
F

Se P é F e Q é F então R será V
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
F v F ^ V -> F^F v V
F ^ V -> F v V
F -> V
V
Conclui-se que vai depender do valor lógico de Q. Então R vai ser V ou F de acordo com o valor de Q. E não sempre Falso como afirma a questão.
Bons estudos a todos!!
R será sempre V.
Retificando o comentário do colega "alucard", nem sempre o valor será V, pois, como diz o enunciado, independente de Q ser V ou F, quando V, o resultado será F, contradizendo assim a generalização do prezado.

Usei a boa e velha tabela verdade:

~P	~Q	P∨Q	P ∧ Q	( P∨Q ) ∧ ( ~ P )	( P ∧ Q ) ∨ ( ~ Q )	( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
F	F	V	V	F	V	V
F	V	V	F	F	V	V
V	F	V	F	V	F	F
V	V	F	F	F	V	V

Colega Bruno Arcari,
Eu também tenho dificuldades em estudar lógica e o único "macete" que encontrei foi estudar muito esta matéria.
Fiz curso isolado, assisti todas as aulas do site euvoupassar (Prof. Tiago Pacífico) e resolvo muitas questões em pelo menos 1 dia da semana.

Força de vontade, determinação e fé em Deus chegaremos lá.
Fiz exatamente como a colega Michelle Canto.
Resolvi a questão com VALOR DE Q(FALSO) E Q(VERDADEIRO) preservando o P que foi dado como falso no enunciado da questão!
Fiz desta forma para economizar tempo, que é muito precioso nas nossas provas.
Admiro os colegas que conseguem inferir com segurança, apenas pelos conectivos. Ainda não cheguei neste nível.
Não sei se fiz certo, porém acertei a questão. Caso eu tenha feito errado, por favor me corrijam.
Só temos duas opções para o Q: V e F
opção 1: colocando o q com V e permanecendo o P como F, conforme o enunciado:
(F v V) ^ V -> (F ^V) v F =
V ^V -> F v F=
V -> F= F ( na condicional a unica combinação que dá Falso é VF)

Opção 2: colocando o q com F e permanecendo o P como F, conforme o enunciado:
(F v F) ^V -> (F v F) v V=
F ^ V -> F v V=
F -> V= V ( na condicional quando a primeira for F, independente do valor lógico da segunda, a proposição será Verdadeira.)

Sendo assim, os resultados, nas duas opções são distintos, tornando a questão errada.
GABARITO: ERRADO

Senhores, não precisamos complicar o que se pode fazer de maneira simples, matei a questão com menos de um minuto sem sequer pegar a caneta! Leia...

Primeiramente, se você está com dificuldade nessa matéria, não tem mistério: DECORE a tabela-verdade. "Mas a matéria de lógica eu não preciso entender?" Sim e Não, pra essa parte da matéria, se você não tiver decorado a tabela, pode até achar respostas, mas vai levar um tempo que na hora da prova você não terá, portanto, DECORE:
http://1.bp.blogspot.com/_ivjE3SCM2dY/TC63urmmpdI/AAAAAAAAC0A/_bMuIccc0zg/s1600/Quest%C3%A3o+166-1.JPG

RESOLUÇÃO:

( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )

Diz a questão: P = "F", Q pode ser "V" ou "F", mas o resultado será sempre "F"

Observe que numa CONDICIONAL, se V → F = F mas se (independente de ser V ou F) → V = V será verdadeiro sempre

Portanto, basta que a "segunda parte" ( P ∧ Q ) ∨ ( ~ Q ) tenha a mera POSSIBILIDADE de ser VERDADEIRA

Conforme já estabelecido pela questão: P = "F"
Consideremos que Q pode ser "V" ou "F", podemos escolher. Vamos atribuir um valor "F": Q = "F"

( P ∧ Q ) v ( ~ Q )
( F ∧ F ) v ( ~ F )
F v V = V

Logo, temos que: (independente de ser V ou F) → V = V repare que o resultado, nesse caso, vai ser SEMPRE verdadeiro, contrariando a questão, que afirmou não haver essa possibilidade e, consequentemente, o item está errado.

Talvez pareça complicado, mas com o tempo a gente pega o jeito da coisa!
A dificuldade é para todos, fé, foco e persistência! Forte abraço
Analisando a questão,

RESPOSTA: ERRADO
Senhores, sei que cada um tem uma maneira de estudar, contudo numa questão simples como esta utilizem a tabela verdade é o método mais seguro, meu resultado após a resolução deu VVFV, então nem sempre dará "F" como afirma a questão, como também nem sempre dará "V", pois temos uma contingência.
"Estude, pois a consequência lógica deste estudo será tua aprovação".
Sem tabela, só precisam ser feitos duas verificações para constatar o valor da conclusão. Sabe-se que o valor de P é falso, então:

1ª hipótese: Q (V):

[(PvQ) ^(¬P)]-->[(P^Q)v(¬Q)]
[(f v v)^(v)] -->[(f^v)v(f)]
[v^v] -->[fvf]
v--->f FALSA

2ª hipótese: Q (F)

[(PvQ) ^(¬P)]-->[(P^Q)v(¬Q)]
[(f v f)^(v)] -->[(f^f)v(f)]
[f^v] -->[fvf]
f--->v VERDADEIRA

Portanto, se o Q for Verdadeiro, R será falso. Gabarito ERRADO
( P v Q ) ^ ( ~P ) ----> ( P ^ Q ) v ( ~Q )
F V F
____________
F

Vou parar por aqui, já é o suficiente para resolver a questão, neste caso, independentemente de qualquer valor adicional,a preposição será verdadeira, pois na tabela verdade da condicional(----> ) só será F quando a primeira preposição for V e a segunda F.
Errado.

Simplifique, doí menos.:-P

Tá vendo o sinal da condicional? Pois é, sabemos que na condicional só é FALSO quando V ---> F.

Suponhamos que P: ( P∨Q ) ∧ ( ~ P )
e que Q: ( P ∧ Q ) ∨ ( ~ Q )

Logo, P-->Q = ?
F --> F= V ou F ---> V= V
Gabarito: ERRADO.

Isso mesmo, Juliana. Também pensei dessa forma.

Na condicional sabemos que só é FALSO quando a primeira proposição tem valor lógico verdadeiro e a segunda falso.

Então, se P é falso, independentemente do valor lógico de Q a proposição já pode ser considerada verdadeira, observem:

R= P ---> Q = F ---> V= V

R= P---> Q = F --->F= V

Qualquer coisa, ficarei grato se mandarem uma mensagem!

Bons estudos! Feliz ano novo!!
Atribuindo valor V para Q, temos:
(F v V) ^ (~F) → (F ^ V) v (~V)

V ^ V → F v F
V→F = F

Atribuindo valor F para Q, temos:
(F v F) ^ (~F) → (F ^ F) v (~F)

F ^ V → F v V

F→V = V

Gab: ERRADO
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
Substituindo P=F
(FvQ)^(V)->(F^Q)v(~Q)
Retirando os elementos neutros...
Q->~Q
fazendo uma mini tabela
V F F
F V V
Gabarito: Errado
GAB. ERRADO

Se "Q" for FALSO, então "R" será VERDADEIRO.

TORNANDO A QUESTÃO ERRADA!
GAB E
O ou é o de boas, e só admite uma falsidade (F v F: F)
Errado, pois dependendo do valor lógico (V/F) atribuído ao '' Q '', a proposição R poderá ser verdadeira ou falsa.
Minha humilde contribuição. Conseguimos matar a questão,rapidamente, pegando apenas a 1a parte

a 2a parte vou chamar de = ?

(P v Q) ^ (~Q) -> (P^Q) v (~Q)
F v F ^ V
F ^ V
F
F-> ? = V
Logo, Gabarito E. A questão erra ao dizer independentemente.

O Q sendo F, R será Verdadeiro!!

Fé na Vitória!!!

ID

599383

Banca

CESPE / CEBRASPE

Órgão

EBC

Ano

2011

Provas

CESPE - 2011 - EBC - Cargos de Nível Superior - Conhecimentos Básicos - Cargo 4 Advocacia

Disciplina

Raciocínio Lógico

Assuntos

Considerando as proposições simples P e Q e a proposição composta R simbolizada por ( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q ), julgue os itens subsequentes.

Considerando todos os possíveis valores lógicos V ou F para as proposições P e Q, é correto afirmar que a proposição (PVQ)Λ(~ P) possui 3 valores lógicos F.

Alternativas

Certo

Errado

Comentários

Resposta: Certo!

Primeiro vamos corrigir o enunciado: Considerando todos os possíveis valores lógicos V ou F para as proposições P e Q, é correto afirmar que a proposição (P v Q) ^ (~ P) possui 3 valores lógicos F.

Agora é só fazer a tabela verdade:

P	Q	~P	(P v Q)	(P v Q) ^ (~P)
V	V	F	V	F
V	F	F	V	F
F	V	V	V	V
F	F	V	F	F

Q199792. Considerando todos os possíveis valores lógicos V ou F para as proposições P e Q, é correto afirmar que a proposição (PvQ)^(~ P) possui 3 valores lógicos F.

Certo ou Errado?

Resolução

Temos todos os possíveis valores lógicos (PvQ)^(~ P):

PvQ ~ P (PvQ)^(~ P)

V V V

V F F

F V F

F F F

Sendo assim, para qualquer valor de P e Q, a preposição (PvQ)^(~ P) terá três valores F.

Item certo

Boa Sorte!
Resposta: Certo!!!
É só construir a tabela verdade:
P Q ~P (P v Q) (P v Q) ^ (~P)
V V F V F
V F F V F
F V V V V
F F V F F
Bons estudos!!!
Decore as regras abaixo e questões como essa você não perde tempo precioso fazendo tabela verdade.
Conjunção (^) (e): Só será VERDADEIRA se ambas as proposições forem VERDADEIRAS. ( V e V);
Disjunção (v) (ou): Só será falsa se ambas as proposições forem FALSAS. (F e F);
Condicional (→) (Se... Então...): Só será FALSA se a primeira proposição (antecedente) for VERDADEIRA e a segunda proposição (consequente) for FALSA. (V e F).
Bicondicional: (<->) (Se e somente se): Só será VERDADEIRO quando as duas proposições forem VERDADEIRAS OU AS DUAS PROPOSIÇÕES FOREM FALSAS. ( V e V); (F e F)
De posse das regras:
Considere como A = (PVQ) e B = (~ P)
A ^ B -> Nessa proposição, onde existe uma CONJUNÇÃO, só existirá um valor lógico VERDADEIRO. Logo, como são duas proposições admitindo-se quatro linhas (já que (~P) é uma negação do P), então, haverá 3 valores lógicos F.

Não Desista!
Bons Estudos.
SÓ LEMBRANDO : PARA SABER QUANTAS LINHAS TEM A COLUNA DA TABELA É SÓ PEGAR 2 ELEVADO AO NUMERO DE PROPOSIÇÕES ( aqui está algo importante - saber o que é prop. simples da composta ) .

NO CASO DA QUESTÃO AQUI : 2 elevado a duas proposições ( o P e ~P é a mesma coisa, visto que a negação só troca o valor logico, não a proposição em si, e é isso que as provas tentam pegar os candidatos despercebidos - mais vc é ninja e sabe disso )

GABARITO CERTO... tem um amigo aqui em baixo que fez a tabela..veja.
Pessoal, a tabela verdade do conectivo conjunção(^) possuem apenas 1 valor verdadeiro e 3 valores falsos, correto a questão.
v /v=v
v / f=f
f / v=f
f / f=f
so da para responder fazendo a tabela... pelo menos nao perde muito tempo fazendo isso
P Q   (P v Q) ^ (~P)

V V    (V v V) ^ (F) = F
V F    (V v F) ^ (F) = F
F V    (F v V) ^ (V) = V
F F    (F v F) ^ (V) = F
Gaba: CERTO!
Dá pra fazer sem usar a Tabela-Veritatis, se não vejamos:
(P v Q) ^ (~ P)
(V v F) ^ (F)
V ^ F
F
Menos tempo perdido!
Analisa-lo-emos quando Q é falso que são 2vezes
teremos (P v F) ^ (~P) = p^~p (famosa contradição) então daqui já temos 2 F
Agora quando Q é verdadeiro que são 2 vezes
(P v V) ^ (~P)= v^(~p)= ~p ~p é V quando p é F e é F quando p é V então temos +1falso

totalizando 3 falsos.
Tabela é pros fracos, valeu!
GAB C
Nem precisa fazer tabela .. basta olhar o símbolo do Λ (exclusivo), que é o conectivo central e que admite apenas 1 verdade e 3 valores falsos, daí já mata a questão.
Minha contribuição.

P..Q..~P....(P v Q) (P v Q) ^ (~P)
V..V....F.........V..................F
V..F....F.........V..................F
F..V....V.........V.................V
F..F....V.........F..................F

Abraço!!!

ID

599749

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Analista de Sistemas Júnior - Engenharia de Software

Disciplina

Raciocínio Lógico

Assuntos

No cálculo proposicional, os operadores lógicos { ¬ , Λ , V , → , ⇔ } podem ser deduzidos a partir dos operadores

Alternativas

{Λ , V }

{¬ ,Λ )

{⇔ , V}

{⇔ ,→ }

{→ ,Λ }

Comentários

Alguém sabe como resolver essa questão??
na verdade não tenho a miníma idéia, mas tenho comigo que os operadores mais complexos "Se,então"; "Se, e somente se", derivem dos mais básicos "não";"E"; "Ou"... mas agora a lógica para se chegar a eles não sei.
Entendo que o operador "não" é básico e não pode ser deduzido.
A única alternativa que contém o "não" é a letra B, portanto é a correta, independente de qualquer outra coisa.
Gostaria que alguém confirmasse se meu raciocínio está correto.
Vamos pegar pelo mais complexo.

Dedução do Bicondicional
p <-> q
Podemos representar equivalentemente como (p -> q) ^ (q -> p), que pode por sua vez, ser representado equivalentemente como (~p v q) ^( ~q v p).
Essa última fórmula pode ainda ser deduzida para através de De Morgan: ~(p ^ ~q) ^ ~(q ^ ~p).
Temos por fim apenas ^ e ~.

Dedução do Condicional
p -> q, equivale a ~p v q, que por sua vez pode ser representado equivalentemente por ~(p ^ ~q).
Temos por fim apenas ^ e ~.

Dedução do OU
p v q equivalente pode ser ~ ~p v ~ ~q. Vale lembrar que Dupla Negação, equivale à própria proposição.
Colocando a negação em evidência, podemos ter ~ (~p ^ ~q).

Portanto, a partir dos operadores ~ e ^, conseguimos deduzir os demais.
Utilizei a lógica da precedência, onde a negação e a conjunção precedem os outros operadores lógicos, logo imaginei que os demais operadores lógicos podem ser deduzidos a partir destes 2. Não sei se minha conclusão está coerente, mas esse pulo do gato me fez acertar a questão. Sempre virão questões assim e o "PULO DO GATO" é a única saída nessas horas!
Significado de A partir de
loc. Gram. Geralmente utilizado para demarcar o início de uma contagem, ordenamento, medida e/ou posição.
Sinônimo de a partir de: a começar de
lógica da precedência do ordenamento: ¬ , Λ , V , → , ⇔ questão B corresponde a ordem( a começar de )
As prioridades são:
~ ^ v --> <-->
De acordo com o cálculo proposicional, é sabido que a prioridade dos operadores lógicos são: {¬, ^, v, → e ←→}.

Assim, os operadores lógicos podem ser deduzidos a partir de “¬” e “^”.

RESPOSTA: (B)
Acertei a questão mas não entendi nada.
Existem situações em que temos sequência de conectivos. Ordem de precedência entre os conectivos:

1º operador: “NÃO”

2º operador: “E”

3º operador: “OU”

4º operador: “SE ENTÃO”

5º operador: “SE E SOMENTE SE”
Vamos para a dedução. Precisamos de dois instrumentos lógicos o "não, ¬" e o "e, ^" e duas proposições arbitrárias
p,q
p sozinha é simples
¬p é a negação de p
p ^ q (conjunção)
negue p e q
¬p v ¬q ( obtemos a disjunção)
faça a equivalência dessa anterior com a condicional
p-->¬q ( obtemos a condicional)
faça essa condicional ir e voltar e teremos a bicondicional
(p-->¬q)^(¬q-->p) é equivalente à p<->¬q (bicondicional)
negue a bicondicional p -v- ¬ q (disjunção exclusiva)
Ufa acabamos...
Mas se quiser continuar a brincadeira, expresse p como conjunto
e coloque um A inteiramente dentro do conjunto p
logo temos para todo A A é p
Agora coloque um B que esteja no conjunto do p mas não inteiramente
logo existe pelo menos um B que é p
Por último coloque um C que não está em p
Nenhum C é p

ID

599755

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Analista de Sistemas Júnior - Engenharia de Software

Disciplina

Raciocínio Lógico

Assuntos

Dadas as proposições atômicas P, Q e R do cálculo proposicional, afirma-se que

Alternativas

¬ (P ∨ Q) ∧ R está na forma normal conjuntiva, e P∧ R, na forma normal disjuntiva.

(P ∨ ¬ Q) ∧ R está na forma normal conjuntiva, e (P ∧ Q) ∨ ¬ R, na forma normal disjuntiva

(P ∨ Q) ∧ R está na forma normal conjuntiva, e ¬ (P ∧ Q) ∨ R, na forma normal disjuntiva.

(P ∨ Q) está na forma normal conjuntiva, e ¬ (P ∧ Q) ∨ R, na forma normal disjuntiva.

(P∧ Q) está na forma normal conjuntiva, e ¬ (P ∨ Q), na forma normal disjuntiva.

Comentários

O que é pedido na questão:
"Dadas as proposições atômicas P, Q e R do cálculo proposicional, afirma-se que
(A) ¬(P ∨ Q) ∧ R está na forma normal conjuntiva, e P ∧ R, na forma normal disjuntiva.
(B) (P ∨ ¬Q) ∧ R está na forma normal conjuntiva, e (P ∧ Q) ∨ ¬R, na forma normal disjuntiva.
(C) (P ∨ Q) ∧ R está na forma normal conjuntiva, e ¬(P ∧ Q) ∨ R, na forma normal disjuntiva.
(D) (P ∨ Q) está na forma normal conjuntiva, e ¬(P ∧ Q) ∨ R, na forma normal disjuntiva.
(E) (P ∧ Q) está na forma normal conjuntiva, e ¬(P ∨ Q), na forma normal disjuntiva."
Não concordo com o gabarito, se alguém souber resolver de forma que a LETRA B seja a correta, poste um recado para mim com o número da questão
COMENTANDO:
a) ERRADO
¬(P ∨ Q) ∧ R => (¬P ∧ ¬ Q) ∧ R está na forma normal conjuntiva ("e") - CERTO
P ∧ R - ERRADO, está na forma conjuntiva ("e")

b) ERRADO
(P ∨ ¬Q) ∧ R está na forma normal conjuntiva ("e") - ERRADO
(P ∧ Q) ∨ ¬R, na forma normal disjuntiva ("ou") - ERRADO

c) ERRADO
(P ∨ Q) ∧ R está na forma normal conjuntiva ("e") - ERRADO
¬(P ∧ Q) ∨ R => (¬P ∨ ¬Q) ∨ R, na forma normal disjuntiva ("ou") - CERTO

d) ERRADO
(P ∨ Q) - ERRADO, está na forma disjuntiva ("ou")
¬(P ∧ Q) ∨ R => ¬(P ∨ ¬Q) ∨ R, na forma normal disjuntiva - CERTO

e) ERRADO
(P ∧ Q) está na forma normal conjuntiva ("e") - CERTO
¬(P ∨ Q) => (¬P ∧ ¬ Q) - ERRADO, está na forma conjuntiva ("e")
Vamos analisar cada uma das assertivas:

A1) ¬(P ∨ Q) ∧ R está na forma normal conjuntiva,
"¬(P ∨ Q) ∧ R", não pode ser analisada diretamente, temos que passar para:
(¬P ∧ ¬Q) ∧ (R ∧R), ou seja, não está em nenhuma forma normal, por isso está errada.

A2) e P ∧ R, na forma normal disjuntiva.
"P ∧ R", não pode ser analisada diretamente, temos que passar para:
(P ∨ P) ∧ ( R ∨ R), ou seja, está na forma normal conjuntiva.

A) A1 está errada e A2 está errada.

---------------------------------------------------------------------------------------------

B1) (P ∨ ¬Q) ∧ R está na forma normal conjuntiva,
(P ∨ ¬Q) ∧ R <==> (P ∨ ¬Q) ∧ (R ∨ R) e está na fnc.

B2) e (P ∧ Q) ∨ ¬R, na forma normal disjuntiva.
(P ∧ Q) ∨ (¬R ∧ ¬R) e está na fnd.

B) B1 correta e B2 correta. GABARITO

---------------------------------------------------------------------------------------------

C1) (P ∨ Q) ∧ R está na forma normal conjuntiva,
(P ∨ Q) ∧ R <==> (P ∨ Q) ∧ (R ∨ R) e está na fnc.

C2) e ¬(P ∧ Q) ∨ R, na forma normal disjuntiva.
(¬P ∨ ¬Q) ∨ (R ∨ R), não está em nenhuma forma normal.

C) C1 correta e C2 errada.

---------------------------------------------------------------------------------------------

D1) (P ∨ Q) está na forma normal conjuntiva,
(P ∨ Q) <==> (P ∧ P) ∨ (Q ∧ Q) e está na fnd.

D2) e ¬(P ∧ Q) ∨ R, na forma normal disjuntiva.
¬(P ∧ Q) ∨ R <==> (¬P ∨ ¬Q) ∨ (R ∨ R) e não está em nenhuma forma normal.

D) D1 errada e D2 errada.

---------------------------------------------------------------------------------------------

E1) (P ∧ Q) está na forma normal conjuntiva,
(P ∧ Q) <==> (P ∨ P) ∧ (Q ∨ Q) e está na fnc.

E2) e ¬(P ∨ Q), na forma normal disjuntiva.
¬(P ∨ Q) <==> (P ∧ ¬Q) <==> (P ∨ P) ∧ (¬Q ∨ ¬Q) e está na fnc.

E) E1 correta e E2 errada.
ALGUÉM PODE EXPLICAR ESSE GABARITO?

Ao meu ver, iria na letra E.
Ao simples fato de analisar os conectivos, concluirmos gabarito B. ^ + v = B
ou fazer eliminação e ficar com a mais certa.
Uma boa explicação a respeito das Formas Normais Conjuntivas e Disjuntivas tem aqui neste site > http://www.pucsp.br/~logica/Proposicional2.htm
Uma fórmula é normal conjuntiva (FNC) se, e somente se:

a) no máximo contem os conectivos ~, ∨ e ∧ ;

b) ~ somente tem alcance sobre as letras proposicionais;

c) não aparecem sinais de negação sucessivos como ~ ~ ;

d) ∨ não tem alcance sobre ∧ , isto é, não há expressões do tipo p ∨ ( q∧ r ).

Exemplos: (~p ∨ q ) ∧ (r ∨ s ∨ p ) , ~ p ∨ q , ~q

Uma fórmula é normal disjuntiva (FND) se, e somente se:

a) no máximo contem os conectivos ~ , ∧ e ∨ ;

b) ~ somente tem alcance sobre as letras proposicionais;

c) não aparecem sinais de negação sucessivos como ~ ~ ;

d) ∧ não tem alcance sobre ∨ , isto é, não há expressões do tipo p ∧ ( q ∨ r ).

Exemplos: p ∨ (q ∧ r ) ∨ (∼ q ∧ p ) , ~ p ∧ q , ~q , ~ p ∨ q

ID

607156

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Analista de Sistemas Júnior - Processos de Negócios - 2011

Disciplina

Raciocínio Lógico

Assuntos

No cálculo proposicional, dada a fórmula (P → Q) → (¬ P Λ Q), exatamente em quantas valorações do par (P, Q) essa proposição assume o valor verdade?

Alternativas

Comentários

Gabarito Letra C

(P → Q) → (¬ P Λ Q)

(V → V) → (F Λ V)
          V → F
            F

(F → F) → ( V Λ F)
     V → F
            F

(F → V) → ( V Λ V)
       V → V
            V

(V → F) → ( F Λ F)
         F → F
           V

Portanto só será 2 vezes

bons estudos

ID

607165

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Analista de Sistemas Júnior - Processos de Negócios - 2011

Disciplina

Raciocínio Lógico

Assuntos

Considere as cláusulas C1 e C2, representadas, respectivamente, pelos conjuntos { ¬ A(x),B(x)} e { A(g(y)),B(y)}.
Um resolvente dessas cláusulas é

Alternativas

{B(x), B(y)}

{B(g(y)), B(y)}

{ ¬ A(x), A(g(x))}

{¬ A(x), A(g(x)), B(x)}

{¬ A(x), B(x), A(g(y)), B(y)}

Comentários

Entendi nada dessa questão.
Eu consegui chegar na resposta da questão pensando em conjuntos...
{ ¬ A(x),B(x)} - Se o elemento "x" não está no conjunto A, então ele está no conjunto B.
{ A(g(y)),B(y)} - Se o elemento "y" está no conjunto G, e G pertence ao conjunto A, logo ele também pertence ao conjunto B.
Sendo assim, eu imaginei o elemento B sendo o Universo, e os conjuntos A e G estariam dentro dele.
Logo a única resposta que faz sentido seria...
{B(g(y)), B(y)} - Se o elemento "y" está no conjunto G, o qual está dentro do conjunto B, logo "y" pertence ao conjunto B.

Nesse raciocínio as demais questões não fariam sentido, porém não sei se é o raciocínio correto. =/

ID

607168

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Analista de Sistemas Júnior - Processos de Negócios - 2011

Disciplina

Raciocínio Lógico

Assuntos

Considere as proposições a seguir.

I - ¬ ( A Λ B ) ↔ ( A → ¬ B)

II - ¬ (A→ ¬ B) → ((A V ¬ B ) Λ (¬ A V B))

III - ((A→ B) → A) → A

IV - ((A V B) Λ (¬ A V C )) → (B V C )

São tautologias as proposições apresentadas em

Alternativas

I e IV, apenas.

II e III, apenas.

I, II e III, apenas.

II, III e IV, apenas.

I, II, III e IV.

Comentários

Gabarito Letra E

Todas são tautológicas, para saber se há tautologia, atribui para todas as proposições simples o valor F
A = F
B = F
C = F

¬ ( A Λ B ) ↔ ( A → ¬ B)
¬ ( F Λ F ) ↔ ( F → V)
¬ F↔ V
V↔ V = VERDADEIRO

¬ (A→ ¬ B) → ((A V ¬ B ) Λ (¬ A V B))
¬ (F→ V) → ((F v V) Λ (V v F))
¬ V → (...)
F → (...) independentemente do valor aqui a sentença será VERDADEIRA.

((A→ B) → A) → A
((F→ F) → F) → F
(V → F) → F
F → F = VERDADEIRO

((A V B) Λ (¬ A V C )) → (B V C )
((F V F) Λ (V v F)) → (F v F)
F Λ V → F
F → F = VERDADEIRO

bons estudos
Renato, sempre funciona?
Dica do Renato funciona. Senão estamos lascados. Fiz a tabela e leva muito tempo.
Não funciona sempre. Não tenho o código aqui agora, mas já fiz questões que esse macete não funfou.
Eu fiz diferente, como o avaliador não disse que era falsa, considerei tudo como verdade. Só coloquei como falsa as que estão com símbolo de negação.

A = V, B = V e C = V

Lembrem-se, é importante saber a precedência das operações, sempre devemos começar pelos parenteses.
Ordem de precedência dos conectivos: ~ ∧ ∨ ∨ → ↔

Vamos às operações:

I - ¬ ( A Λ B ) ↔ ( A → ¬ B)
¬ ( V Λ V ) ↔ ( V → F)
¬ V ↔ F
F ↔ F
V - Verdadeiro

II - ¬ (A→ ¬ B) → ((A V ¬ B ) Λ (¬ A V B))
¬ (V→ ¬F) → ((V V F ) Λ (F V V))
¬ (V) → ((V ) Λ (V))
F → V
V - Verdadeiro

III - ((A→ B) → A) → A
((V→ V) → V) → V
( V → V) → V
V → V
V - Verdadeiro

IV - ((A V B) Λ (¬ A V C )) → (B V C )
((V V V) Λ (F V V)) → (V V V )
(V Λ V) → V
V → V
V - Verdadeiro

Espero ter ajudado.
Rascunho para itens I e II

A ~A B ~B
V F   V F
V F   F V
F V   V F
F V   F V

I)

A^B ~(A^B) A->~B <->
V F F V
F V V V
F V   V V
F V   V V (Tautologia)

II)

A->~B ~(A->~B)
F V
V F
V F
V F

Logo: Como no item II temos o operador -> o pedaço ((Av~B)^(~AvB)) não pode ser Falso para primeira linha

(Av~B) ~AvB ((Av~B)^(~AvB))
V V V

Tautologia.

Apenas as opções de resposta C e E tem I e II como tautologias, e em ambas temos a opção III como tautologia, logo não precisamos fazer a tabela verdade da opção III só precisamos fazer da opção IV.

IV)

A ~A B C (AvB) (~AvC) ((AvB)^(~AvC)) (BvC) ->
V F V V V V V V V
V F V F V   F F V V
V F F V V V V V V
V F F F V F F F V
F V V V V V V V V
F V V F V V V V V
F V F V F V F V V
F V F F F V F F V

Tautologia.
CUIDADO

Testei o esquema do Renato em vários casos e funcionou de fato, mas neste aqui não:

((P e Q) ---> R) ou R

Assumindo F para todas as letras:

((F e F) ---> F) ou F

(F ---> F) ou F

V ou F = V.... mas a proposição é FALSA para P=V;Q=V;R=F

Substituindo os alores na fórmula:

((V e V) ---> F) ou F

(V ---> F) ou F

F ou F = F...logo, não é tautologia...

ID

607174

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Analista de Sistemas Júnior - Processos de Negócios - 2011

Disciplina

Raciocínio Lógico

Assuntos

Considere as sentenças da lógica de primeira ordem a seguir.

I - ∃x ∃y A(x,y) Λ ¬ ∃x A(x,x)

II - ∀ x ∀y A (x,y) Λ ¬ ∀ x A (x,x)

III - ∀ x ∀ A ( x, y) → ¬ ∀ xA (x, x)

São insatisfatíveis APENAS as sentenças apresentadas em

Alternativas

III

I e II

II e III

Comentários

Reconhecer o tipo de uma sentença facilita a sua tradu¸cão para a linguagem da l´ogica de predicados. Veja outros exemplos:

– “Toda cobra ´e venenosa”: ∀X[cobra(X) → venenosa(X)]

– “Os rem´edios s˜ao perigosos”: ∀X[remedio(X) → perigoso(X)]

– “Nenhuma bruxa ´e bela”: ∀X[bruxa(X) → ¬bela(X)]

– “Alguns políticos não são honestos”: ∃X[politico(X) ∧ ¬honesto(X)]
é inglês? kkkk

ID

609628

Banca

PONTUA

Órgão

TRE-SC

Ano

2011

Provas

PONTUA - 2011 - TRE-SC - Técnico Judiciário - Área Administrativa

Disciplina

Raciocínio Lógico

Assuntos

Sejam as seguintes proposições P: Carlos fala francês, Q: Carlos fala inglês e R: Carlos fala alemão. Dada a seguinte proposição:

É falso que Carlos fala inglês ou alemão, mas que não fala francês.

Assinale a alternativa que traduz de maneira CORRETA a proposição acima para a linguagem simbólica:

Alternativas

~((Q∨ R)∧~ P).

(P∨Q)∧~R.

~ (P∧~R).

(P∧Q)∨~(P∧R).

Comentários

Pessoal,

Essa calculadora pode auxiliá-los a compreender as nomenclaturas: http://www.calculadoraonline.com.br/tabela-verdade
GABARITO A
É FALSO QUE CARLOS FALA INGLÊS (~Q) OU ALEMÃO (R) E NÃO FALA FRANCÊS (~P)
Logo,
~((Q∨R)∧~P)
DICA: Sempre que aparecer "É falso que" , "É mentira que" , substitua pela negação.

Outra parte que pode confundir é o conectivo "MAS". Observe que ele dá ideia de simultaneidade, poderia ser substituído pelo "E".
A questão nos deu as seguintes proposições representadas pelas letras logo a frente destas:
P: Carlos fala francês
Q: Carlos fala inglês
R: Carlos fala alemão
Mas para resolver você tem que saber também que a disjunção ("OU") é simbolizada por v; que a negação pode ser simbolizada por ~ ; e que o "mas" nesse caso terá o mesmo simbolo da conjunção ^ . Então, vamos substituí-las:
É falso que Carlos fala inglês ou alemão, mas que não fala francês.
~ Q v R ^ ~ P
Ou seja, incluindo-se os parenteses para organização, vemos que a resposta é
~((Q∨ R)∧~ P), "letra A"
Essa questão resolvi por eliminação, vejam como resolvi. A afirmativa diz o seguinte: "É falso que Carlos fala inglês ou alemão, mas que não fala francês". Nas alternativas a única que começa com a proposição Q, ou seja, Carlos fala inglês é a letra A.
Veja o vídeo que gravei com a resolução dessa questão:
https://youtu.be/R6Hl0W8n8dU
Professor Ivan Chagas
esse já passou no concurso só ficou aqui a alma pra nos inspirar

ID

609820

Banca

PONTUA

Órgão

TRE-SC

Ano

2011

Provas

PONTUA - 2011 - TRE-SC - Analista Judiciário - Área Judiciária

Disciplina

Raciocínio Lógico

Assuntos

Sejam as seguintes proposições P: Marcos é alto, Q: Marcos é elegante. Dada a seguinte proposição:
Não é verdade que Marcos é baixo ou elegante.
Assinale a alternativa abaixo que traduz de maneira CORRETA a proposição acima para a linguagem simbólica:

Alternativas

~ P ∧ ~ Q.

P ∨ (~ P ∧ Q).

~ (~ P ∨ Q).

~ (~ P ∨ ~ Q).

Comentários

Temos que desmembrar a frase.

P: Marcos é alto,
Q: Marcos é elegante

1º - NÃO É VERDADE = NEGAÇÃO (~)
2º - marcos é baixo = ~P (Negação de P, já que marcos é alto.)
3º - e = ^ (conjunção)
4º - elegante = Q

Juntando a frase temos:
Não é verdade (~) que Marcos é baixo(~P)e(^)elegante(Q..)
~(~P^Q)
Não concordo com a questão uma vez que a negação de "Marcos é alto" seria "Marcos não é alto" e jamais "Marcos é baixo"

Marcos também poderia ser de estartura mediana, correto.
Marcos é baixo não é negação e sim oposto de Marcos é alto.
Negação é: Não é verdade que Marcos NÃO É ALTO.
Galera, aqui estão os significados dos símbolos:

CONECTIVO NOTAÇÃO DENOMINAÇÃO E ^ Conjunção Ou V Disjunção Então ... --> Condicional Se e somente se <-> bicondicional Não ~ Negação
Tendo em vista isso, sendo as proposições P: Marcos é alto, Q: Marcos é elegante. Dada a seguinte proposição:
Não é verdade que Marcos é baixo OU elegante.

Não e verdade que Marcos é baixo, "então ele é alto": ~(~P)
Ou elegante: v Q, então ficará: ~(~P v Q)
Márcio, você trocou os símbolos não é e (^) é ou (v).
Portanto gab: C

ID

622243

Banca

FCC

Órgão

TRT - 2ª REGIÃO (SP)

Ano

2008

Provas

FCC - 2008 - TRT - 2ª REGIÃO (SP) - Técnico Judiciário - Área Administrativa

Disciplina

Raciocínio Lógico

Assuntos

Dadas as proposições simples p e q, tais que p é verdadeira e q é falsa, considere as seguintes proposições compostas:
(1) p ∧ q ; (2) ~p → q ; (3) ~(p ∨ ~q) ; (4) ~(p ↔ q)
Quantas dessas proposições compostas são verdadeiras?

Alternativas

Nenhuma.

Apenas uma.

Apenas duas.

Apenas três.

Quatro.

Comentários

como vc soube qual conectivo estava no lugar da "?"
Não entendi. Como vc sabe qual conectivo substitui o "?" em cada questão?
Postagem incorreta! Não dá para resolver a questão! Só quem já a viu em outro lugar...
Pessoal, é só ir no arquivo da prova(PDF) e ver o conectivo...

(1) p^q_____________V ^ F = F
(2) ~p->q____________F -> F = V
(3) ~(pv~q)___________~(V v V = V) = F
(4) ~(p<->q)___________~(V<->F = F) = V

Só para não haver dúvidas, resolvi os que estão entre parênteses primeiro...
Assim fica impossível resolver a questão.
sem conectivo fica meio complicado né... aff questões bizarras
Pô galera... mt fácil resolver a questão mesmo não aparecendo os conectivos. Basta vocês clicarem ali no link, em frente o campo "`PROVA" e depois abrir a prova e procura a questão... pra quem ainda tiver com preguiça de fazer isso, os conectivos são:

(1) p ∧ q
(2) ~p → q
(3) ~(p ∨ ~q)
(4) ~(p ↔ q)

Só não resolve agora quem não quiser! kkk
Gab letra C

Eu juro que tentei explicar aqui,mas como sou um tanto ruim de didatica,prefiro "passar a bola" para este otimo video que vi no youtube.Tem varios com todos os conectivos.

Avaliem depois

Raciocínio Lógico 05 - Conectivo se...então - Condicional - YouTube
Se alguém pudesse por gentileza explicar detalhadamente essa questão, o que significam esses símbolos para que eu possa chegar na resposta, eu agradeceria.
E desculpe a ignorância mas isso é grego pra mim, não consegui entender nada, então se alguém souber explicar de uma forma simples e direta será muito válido!

Grata.
Vou tentar, Carolina:

Dadas as proposições simples p e q, tais que p é verdadeira e q é falsa, considere as seguintes proposições compostas:
(1) p ∧ q ; (2) ~p → q ; (3) ~(p ∨ ~q) ; (4) ~(p ↔ q)
Quantas dessas proposições compostas são verdadeiras?

O ~ é a negação da proposição. Assim, quando p for verdadeira, ~p será falsa, por exemplo.
O símbolo ∧ é uma Conjunção. Nela, a proposição composta (p ∧ q) só será verdadeira quando as duas proposições simples que a integram forem verdadeiras tb.
Como a questão afirma que p é verdadeira e q é falsa, a proposição composta 1 [p ∧ q] será falsa.
O simbolo → é uma Condicional. Nela, a proposição composta (~p → q) só será falsa quando a primeira proposição simples for verdadeira e a segunda proposição simples for falsa. Como a questão afirma que p é verdadeira, sua negação (~p) será falsa. Assim, a proposição composta 2 [~p → q] será verdadeira, pois (~p) é falsa e (q) é falsa tb.
O simbolo ∨ é uma Disjunção. Nela, a proposição composta ~(p ∨ ~q) só será falsa quando as duas proposições simples que a integram forem falsas. Como a questão afirma que q é falsa, sua negação (~q) será verdadeira. Assim, (p ∨ ~q) será verdadeira, já que (p) é verdadeira e (~q) é falsa. Mas, a proposição composta é negada fora dos parênteses ~(p ∨ ~q). Sendo assim, como tínhamos afirmado que era verdadeira, com sua negação a proposição composta 3 [~(p ∨ ~q)] será falsa.
Por últímo, temos uma Bicondicional, representada por ↔. Nela, a proposição composta ~(p ↔ q) só será verdadeira quando as duas proposições simples que a integram forem verdadeiras, ou quando ambas forem falsas. Assim, como (p) é verdadeira e (q) é falsa, segundo a questão, a propocição (p ↔ q) será falsa. Porém, como o símbolo de negação a antecede, a proposição composta 4 [~(p ↔ q)] será verdadeira.

Desse modo, a resposta correta é letra C (proposições 2 e 4 são verdadeiras).

Uma dica que um professor deu pra decorar quando uma condicional (aparentemente o mais difícil de lembrar) é falsa, é só pensar em Vera Fischer = Falsa, nessa ordem.
Proposição simples verdadeira, segunda proposição simples falsa, resultado da proposição falso.

Nesse blog tem tabela-verdade pra ficar mais fácil de entender: http://logicocom.blogspot.com.br/2010/06/tabelas-verdade.html
CORRETA: C
Faça a leitura da questão com cuidado, é simples a questão
Definição Proposição Composta.
Sentenças que podem ser fragmentadas em mais de uma proposição.
Ex: Há vida após a morte. Proposição Simples.
Ex: Se passo no concurso, então fico feliz. Proposição Composta.
P ^ Q = V e F = F
~P ---> Q = F então F = V
~P v ~Q = F ou V = V
~(P <---> Q) = F se e somente se F = V
Bons ESTUDOS. RUMO AO DEPEN ou A.P.F
Levando em conta que = P é verdadeiro
Q é falso

(1) P ^ Q : Conjunção = Só é verdadeiro se todas as proposições simples forem verdadeiras

Como Q é falso (dito no enunciado)

A proposição (1) é falsa!

(2) ~P -> Q : Condicional = só é falso se o antecedente for verdadeiro e o consequente falso

Q é falso porém... se P é verdadeiro, (não P) ~P é falso

A proposição (2) é verdadeira!

(3) ~(P v ~Q) : Disjunção = Como o sinal de negação está fora do parênteses, indica que está negando a proposição

P v ~Q
Para negar uma disjunção = nega as proposições simples e troca disjunção "ou" (v) por conjunção "e" (^)
aplicando...

~P ^ Q : Conjunção = Uma conjunção só é verdadeira se todas as proposições simples forem verdadeiras
~P e Q são falsos..

A proposição (3) é falsa!

(4) ~(P <-> Q) : Bicondicional = Para negar um bicondicional é só tranformá-lo em disjunção exclusiva ( V)

P v Q : Disjunção exclusiva = sempre será verdadeira se os valores das proposições simples forem diferentes

P verdadeiro diferente de Q falso

A proposição (4) verdadeira!
Vou tentar explicar a vocês a alterantiva 4

~(p ↔ q) - primeiramente entendam, p é verdadeira e q é falsa, de acordo com o enunciado correto? Como já foi exposto, uma bicondicional somente será falsa quando ambas forem verdadeiras, ou ambas forem falsas. Logo, se negarmos o p e q bicondicional com e seu respectivos valores ficará assim. ~p ↔ ~q correto? Até aê tudo bem, todavia, negando o p que é verdadeiro ele passa a ser falso, e o q que é falso passa a ser verdeiro, pois houve uma NEGAÇÃO, ou seja, troca-se seu valor, negando-o. Entao, devido a isso, a alternativa fica ~p ↔ ~q, visto que o p é verdadeiro e negando-o passa a ser falso e o q e faso que negando-o
f f passa a ser verdadeiro. A grande questão, o P é falso? Não, e o Q é verdadeiro? Também não, logo, ambas são falsas. Pois nem o P e falso, e nem o Q e verdadeiro, logo o valor das duas continua sendo F F, ao contrario do que ela quer demonstrar, ao induzir o candidato que uma e Falso por ser verdadeiro e mudar pra falso, e a outra é verdadeira por mudar pro falso e ser falso, o que nao condiz com a realidade, pois ao negar-se ambas, trocam-se seus valores, que continuam sendo falsos. Espero ter sido claro. É bem complexa a questão, para os que dizem que é simples, com certeza já devem ser Juizes ou promotes, e lhes falta humildade, que é a principal inimiga de quem estuda. Digo por experiências.
aguardo sete dessas na minha prova, (risos)
muito bom, Fernanda!!!!!!!!!!!!!!!!
De acordo com os dados da questão e com a tabela-verdade de cada proposição composta:

p ^ q = V ^ F = F

~p → q = ~V → F = F → F = V

~(p ∨ ~q) = ~(V v ~F) = ~(V v V) = F ^ F = F

~(p ↔ q) = (p ∧ ~q) ∨ (q ∧ ~p) = (V ∧ V) ∨ (F ∧ F) = V v F = V

RESPOSTA: (C)
Ciro Ciarlini, acho que complicou demais algo simples. Além disso, a bicondicional produz o valor verdadeiro se ambas as proposições forem verdadeiras ou ambas falsas, e não o contrário como tu disse.
V V = V
F F = V
V F = F
F V = F
Questão muito boa,ajuda a raciocinar os conectivos lógicos,gostei!
Apenas DUAS
(1) p ∧ q - v e f = F (2) ~p → q = ~(v) → f = (f) → f = V (3) ~(p ∨ ~q) = (~p e q) = f e v = F (4) ~(p ↔ q) = ou p ou q = ou v ou f = V
Para poder responder qq questão de proposição composta, temos que ter um conhecimento básico de CONECTIVOS LÓGICOS.

CONJUNÇÃO: será "V" quando tudo for "V".

DISJUNÇÃO: será "F" quando tudo for "F".

CONDICIONAL: será "F" quando seu antecedente for "V" e seu consequente for "F", dessa forma: V F

DISJUNÇÃO EXCLUSIVA: será "V" quando tudo for diferente => V F, F V

BICONDICIONAL: será "V" quando tudo for igual: => V V, F F

QUESTÃO

1- p ^ q= F

2- ~p->q= V

3- ~(pv~q)= ~p^q = F

4- ~(pq)= p v q= V. Está requer um pouco de atenção, para negar uma BICONDICIONAL, faz uma DISJUNÇÃO EXCLUSIVA. " LEIS DE MORGAN"

BONS ESTUDOS GALERA!!!

___________________

O que queremos? Passar no concurso.

E quando queremos? É irrelevante.
Se P é Verdadeiro e Q é Falsa

Depois é só resolver as proposições:

p ∧ q: Errada pois Q tem que ser Falsa

~p → q: p ∧ ~ q, Certa pois Q fica Falsa

~(p ∨ ~q): ~ p ∧ q, Errada pois Q tem que ser Falsa e P tem que ser Verdadeira

~(p ↔ q): p ∧ ~ q: Certa, pois Q está Falsa e P Verdadeira.

Logo temos apenas duas proposições compostas verdadeiras.
De acordo com os dados da questão e com a tabela-verdade de cada proposição composta:

p ^ q = V ^ F = F

~p → q = ~V → F = F → F = V

~(p ∨ ~q) = ~(V v ~F) = ~(V v V) = F ^ F = F

~(p ↔ q) = (p ∧ ~q) ∨ (q ∧ ~p) = (V ∧ V) ∨ (F ∧ F) = V v F = V

RESPOSTA: (C)

Fonte: QC
Primeiro passo: Tabela verdade

1)

p    q   p ^ q

V    V    V
V    F    F
F    V    F
F    F    F , portanto será F.

2)

p    q    ~p = q

V   V    F     V
V   F    F     F
F   V    V     V
F   F    V     V, portanto será V.

3)

p      q    ~p    ~q ~p * q

V     V   F      F       F
V   F   F        V       F
F   V       V        F       F
F   F       V        V       V, portanto será F.

4)

p       q       ~p      ~p=q

V       V       F         F
V       F       F         V
F       V       V         V
F       F       V         F, portanto será V.

Segundo Passo: Analisar

Há então duas verdadeiras, letra C.

Símbolos:

= é bicondicional;

* é dinjunção.
Macete do "Se... então":

Só a Vera Fischer é Falsa!

V->F - F

Todas as demais serão verdadeiras!
De acordo com os dados da questão e com a tabela-verdade de cada proposição composta:

p ^ q = V ^ F = F

~p → q = ~V → F = F → F = V

~(p ∨ ~q) = ~(V v ~F) = ~(V v V) = F ^ F = F

~(p ↔ q) = (p ∧ ~q) ∨ (q ∧ ~p) = (V ∧ V) ∨ (F ∧ F) = V v F = V
Cuidado...Bicondicional >iguais da Verdadeiro

ou exclusivo>diferentes da verdadeiro.

Essa foi a parte principal da questão.
Vejamos a solução mais rápida, através da tabela verdade. Do enunciado, sabemos que p é V e q é F.

Resposta: C.
Até eu que odeio essa matéria achei a questão top kkkkkk

Essa sim mede conhecimento sem pegadinha fdp!

Abraços e até a posse!
Ao meu ver, nenhuma delas são proposições compostas, mas são todas simples. Posso estar enganado?
C
Apenas duas.

ID

638137

Banca

FUMARC

Órgão

PRODEMGE

Ano

2011

Provas

Disciplina

Raciocínio Lógico

Assuntos

Considere as duas proposições abaixo em que Q representa o conjunto dos números racionais.

(I) (∀x ∈ Q) (∀y ∈ Q) (x< y -> (∃r ∈ Q) (x< r < y)).

(II) (∃q ∈ Q) (∀r ∈ Q) (r>0 -> 0 ≤ q< r).

Supondo que (I) e (II) sejam verdadeiras, é CORRETO afirmar que

Alternativas

q > 0.

q < 0.

q = 0.

q = 1.

Comentários

Aparece apenas interrogações, alguem me da uma luz?
sou bom de chute, acertei, mas entender que é bom nada. alguém sabe resolver isso?
a interpretação geral nos serve para chegar a resposta certa, o ideal é necessario analisar todos elementos da questão, estetica, conteudo e aplicação teorica.

No meu caso eu fiz o seguinte, I e II, FF= F ou FF= V como a questão informa que são iguais e verdadeiras logo temos que a logica é FF= V.
Espera um pouco: 0 é um número racional?
LETRA C

(I) (∀x ∈ Q) (∀y ∈ Q) (x< y -> (∃r ∈ Q) (x< r < y)) -> Leitura= Para todo X pertencente aos número Racionais, todo Y pertence aos Racionais, tal que: Se y maior que x então(Existe pelo menos um r pertencente aos número Racionais tal que r é maior que x e menor que y) - Essa primeira proposição é totalmente dispensável para a resolução da questão.

(II) (∃q ∈ Q) (∀r ∈ Q) (r>0 -> 0 ≤ q< r) -> Leitura= Existe pelo menos um q pertencente aos racionais, para todo r pertencente aos racionais tal que se r maior que 0 então q maior ou igual a 0 e menor do que r.

O importante agora e testar as respostas na segunda proposição:

b) q < 0 -> A proposição II fala que q tem que ser MAIOR OU IGUAL A 0, logo essta está dispensada
a) q > 0 -> A proposição diz: "Para todo r pertencente aos Racionais tal que se r>0..." logo o r pode ser 0,00000001 se q for 0,1 a condição não é satisfeita, já que estamos falando PARA TODO R
d) q = 1 -> 1 é maior do que 0, logo caímos no problema anterior
c) q = 0 -> Eliminando as demais temos essa como certa, reparem que se q for igual 0 qualquer número de r maior do que 0 satisfaz a proposição II

ID

672268

Banca

CONSULPLAN

Órgão

TSE

Ano

2012

Provas

CONSULPLAN - 2012 - TSE - Técnico Judiciário - Área Administrativa

Disciplina

Raciocínio Lógico

Assuntos

Observe as proposições lógicas simples P, Q e R.

• P: Hoje é dia de Natal.

• Q: Eu vou ganhar presente.

• R: A família está feliz.

As proposições ~P, ~Q , ~R são, respectivamente, as negações das proposições P, Q e R. O conectivo “e” é representado pelo símbolo ∧, enquanto o conectivo “ou” é representado por ∨ . A implicação é representada por →.

A proposição composta (~P ∧ R) → Q corresponde a

Alternativas

Hoje é dia de Natal e a família está feliz e eu vou ganhar presente.

Hoje não é dia de Natal e a família está feliz ou eu vou ganhar presente.

Se hoje não é dia de Natal e a família está feliz então eu vou ganhar presente.

Se hoje é dia de Natal ou a família está feliz então eu vou ganhar presente.

Comentários

• P: Hoje é dia de Natal. • Q: Eu vou ganhar presente. • R: A família está feliz. (~P ∧ R): Hoje não é dia de Natal e a família está feliz. (~P ∧ R) → Q: Se Hoje não é dia de Natal e a família está feliz então eu vou ganhar presente.
nao entendi... o pq da modificação da frase...
É complicado quando se tem interrogações nos lugares dos conectivos.
Apesar de ter acertado a questão, eu acredito que a proposição composta "Hoje não é dia de Natal e a família está feliz ou eu vou ganhar presente" também está correta.
você tem uma condicional (~P ? R) - Q
você tem 2 opções
(~P ^ R) - Q
(~p ou R ) - Q

P Hoje é dia de Natal
Q Eu vou Ganhar presnte
R A família está feliz
como é uma condicional e o parêntesis no inicio o Se vem antes na frase e depois o então

Se  hoje não é dia de natal  e a família está feliz então eu vou ganhar presente
Se hoje não é dia de natal ou a família está feliz então eu vou ganhar presente

A respota é Se  hoje não é dia de natal  e a família está feliz então eu vou ganhar presente letra C
Na verdade a proposição composta está desconfigurada aqui no site QC, na prova ela apareceu da seguinte forma: (~P ^ R) -> Q

Bons estudos!
P : Hoje é dia de Natal.
Q : Eu vou ganhar presente.
R : A família está feliz.
(~P ^ R): Hoje não é dia de Natal e a família está feliz.
(~P ^ R) -> Q : Se hoje não é dia de Natal e a família está feliz então eu vou ganhar presente.
Resposta Letra "C".
Questão pra vc não zerar na prova :D
somente para representar os simbolos em frases
Que fácil...

Podia ser sempre assim :/
sério isso?
Assita à resolução desta questão no Youtube em https://youtu.be/gBVE2qqSRpY
Olá pessoal,

Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/OJP2dYAx5KA

Professor Ivan Chagas
www.gurudamatematica.com.br
        Como “P = Hoje é dia de Natal”, então:
~P = Hoje NÃO é dia de Natal

               Assim, a conjunção (~P ∧ R) pode ser escrita como:
“Hoje NÃO é dia de Natal E a família está feliz”

               Portanto, a condicional (~P ∧ R) → Q corresponde a:
“SE hoje não é dia de Natal e a família está feliz, ENTÃO eu vou ganhar presente”
Resposta: C

ID

683818

Banca

MOVENS

Órgão

Prefeitura de Manaus - AM

Ano

2010

Provas

MOVENS - 2010 - Prefeitura de Manaus - AM - Analista - Fisioterapia

Disciplina

Raciocínio Lógico

Assuntos

A lógica é a “arte do bem pensar”, defendem alguns autores. As fórmulas bem formadas da linguagem da lógica proposicional são construídas a partir de símbolos do alfabeto e de várias regras.

– Este animal é um coelho ou um cachorro.
– Não é um coelho.
– Logo, é um cachorro.

Acerca das proposições acima, assinale a opção correta.

Alternativas

(p ∨ q) ∧ ~ p ∴ q

(p ∧ q) ∧ ~p ∴ q

(p → q) ∧ ~p ∴ q

ID

683821

Banca

MOVENS

Órgão

Prefeitura de Manaus - AM

Ano

2010

Provas

MOVENS - 2010 - Prefeitura de Manaus - AM - Analista - Fisioterapia

Disciplina

Raciocínio Lógico

Assuntos

A sentença “Hoje não nevou, então Lucas não foi patinar e Gustavo não foi à escola” é corretamente representada por

Alternativas

~p ∨ (~r ∧ ~q)

~p ∧ (~ r ∨ ~ q)

~p → (~r ∧ ~ q )

p → (~r ∧ ~q)

ID

706531

Banca

CESPE / CEBRASPE

Órgão

TC-DF

Ano

2012

Provas

CESPE - 2012 - TC-DF - Auditor de Controle Externo

Disciplina

Raciocínio Lógico

Assuntos

Com a finalidade de reduzir as despesas mensais com energia elétrica na sua repartição, o gestor mandou instalar, nas áreas de circulação, sensores de presença e de claridade natural que atendem à seguinte especificação:

P: A luz permanece acesa se, e somente se, há movimento e não há claridade natural suficiente no recinto.

Acerca dessa situação, julgue os itens seguintes.

A especificação P pode ser corretamente representada por p ↔ (q Λ r ), em que p, q e r correspondem a proposições adequadas e os símbolos ↔ e Λ representam, respectivamente, a bicondicional e a conjunção

Alternativas

Certo

Errado

Comentários

Perfeito!
A especificação P pode ser corretamente representada por p↔(q^r), em que p, q e r correspondem a proposições adequadas e os símbolos ↔ e ^ representam, respectivamente, a bicondicional e a conjunção.
Depois da bicondicional (↔) aparecem duas proposições ligadas pela conjunção: (q) há movimento e (r) não há claridade natural suficiente no recinto.
A especificação P pode ser corretamente representada por p ↔ (q Λ r ), em que p, q e r correspondem a proposições adequadas e os símbolos ↔ e Λ representam, respectivamente, a bicondicional e a conjunção

Péssima digitação. Não sei como o colega acima conseguiu fazer a questão nestas condições!!!
Vacilei no "r", pois como a frase é uma negação pensei que seria "~r".
Eu tive a mesma dúvida do colega acima.

Porque não é ~r?
Temos que tirar da cabeça que se em uma proposição aparecer um "não" ela será ~p (exemplo)

A questão mostra um proposição já feita "Não há claridade natural", portanto a negação seria "Há claridade natural".

Bons estudos.
As proposições estão corretas, mas interpretei da seguinte maneira ( P ↔ Q) Λ R. Acredito que foi falta de interpretação mesmo, pois a primeira parte da questão no meu ponto de vista P: Luz a acesa se e somente se Q: Há movimento.
Certo
Pessoal acho que para resolver a questão deve-se interpretar o PODE!!!
Claro, como falou os colegas, que já existe uma bicondicional pronta (P:), mas a questão perguntou se ela PODE ser representada por p ↔ (q Λ r ). PODE para isso basta que p, q e r sejam falsos, na bicondicional F e F é verdadeiro.
A especificação P pode ser corretamente representada por p ↔ (q Λ r ), em que p, q e r correspondem a proposições adequadas e os símbolos ↔ e Λ representam, respectivamente, a bicondicional e a conjunção.correto- os símbolos representam bicondicional (tb =)& conjunção ('&'; '/\'). p & r são as outras proposições:, há movimento e não há claridade natural suficiente no recinto.
Finalmente o pessoal do CESPE/UNB criou juízo e está elaborando questões sensatas. (Depois de tantas reclamações)
P: a luz permanece acesa se, e somente se, há movimento e não há claridade.
Destrinchando a proposição:
p: a luz permanece acesa;
q: há movimento;
r: não há claridade;
sendo:
<-> o símbolo da bicondicional "se, e somente se"; e
Λ o símbolo da conjunção "e".
Dessa forma, a representação simbólica da proposição P é:
p <-> (q Λ r)
Portanto, questão correta.
Procedi da seguinte maneira: há três verbos na frase, ou seja, três proposições logicas, que podem ser valoridas (atribuir valor)
PRIMEIRA: a luz PERMANECE acessa, que denominarm p
SEGUNDA; Há movimento, deniminaram q
TERCEIRA: não HÁ claridade natural suficiente no recinto, denominaram r
São dois os conectivos: SE, SOMENTE SE (bicondicional) representado por: <---> ; E (conjunção) ^
Assim temos p <---> ( q^ r)
r não está negativo porque a proposição indica que há claridade, embora,não seja suficiente.
Destrinchando a proposição:

p: a luz permanece acesa;

q: há movimento;

r: não há claridade;

Bem o que a Kémmely disse mesmo.
Coloquei a alternativa como errada. O meu raciocínio foi que primeiro devemos resolver o "se somente se" e depois o "e", desta forma ficaria assim: (p<->q)^r
Alguém pode me ajudar?
sacanagem do cespe em considerar o "não" parte da proposição ao invés de negação... tenho feito questões do cespe e sempre, SEMPRE o maldito considera o não como negação sem deixar claro.... Agora me diz, como adivinhar quando o não é negação ou parte da proposição? Como saber se o cara que escreveu a frase "Marcelo não é gordo" tah falando que isso é A ao invez de ~A?
exemplos onde o cespe considera o não como negação sem deixar claro Q88402 , Q259810, e varias outras que o "não" aparece( preguiça de ficar caçando elas aqui)..se eu fosse considerar o "não" como parte da proposição ao invéz de negação da proposição teria errado.

Anita
P se somente se ( Q e R)
a luz acende se e somente se 1- tem movimento E 2- nao tem luz
Não sei te explicar cara, na leitura ficou claro pra mim q a luz só acende se tem movimento e não tem luz natural( as duas coisas juntas).. pela sua lógica a luz acende se tem movimento...e depois de acesa ela vai verificar se tem luz natural e se caso tiver ela apaga... não a luz não acende...pois tem 2 coisas que precisam estar acontecendo juntas pra q ela acenda.. a condição (Q e R) não se separa ... pra , sei lá, ficar mais facil de entender chame (Q e R) de S.... P se somente se S
O CESPE só quis saber se a estrutura lógica estava correta, independente do valor lógico das proposições
Tão certo quanto o ar que eu respiro, aleluia.
De acordo com o enunciado, considera-se convenientemente as seguintes proposições simples:

p:            “A luz permanece acesa."

q:            “Há movimento."

r:             “Não há claridade natural suficiente no recinto."

                Sendo assim, a especificação P pode ser escrita: p ↔ (q Λ r )

RESPOSTA: CERTO
Questão perfeita!
Já errei uma questão por isso e aprendi a regra:

Uma negação (¬ ou ~) é uma MODIFICAÇÃO no valor lógico.

O fato de ter um "não" não quer dizer que é uma negação
Só vai ser uma negação se alterar o valor lógico.
Exemplo:
P: o céu é azul (é uma sentença)
~P: o céu não é azul (é a negação dessa sentença)
Porém, a sentença poderia vir:
P: o céu não é azul (é uma sentença)
~P: o céu é azul (é a negação dessa sentença)

Simples!
Obrigada Lucas, minha dúvida foi exatamente sobre isso!

ID

773794

Banca

CESPE / CEBRASPE

Órgão

MEC

Ano

2011

Provas

CESPE - 2011 - MEC - Nível Superior - Conhecimentos Básicos - Todos os Cargos

Disciplina

Raciocínio Lógico

Assuntos

Se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (PV¬Q)→(P∧R) será falsa.

Alternativas

Certo

Errado

Comentários

Gabarito errado

A questão informa que apenas uma será verdadeira. Vamos resoolver por hipóteses

1º situação: P(V) ; Q(F); R(F) = então a preposição será falsa;

2º situação: P(F) ; Q(V); R(F) = então a preposição será Verdadeira. Na condicional, caso o antecedente for falso, pouco importa o consequente, será verdadeiro.

3º situação: P(F) ; Q(F); R(V) = então a preposição será falsa.
Contruindo a tabela verdade verifica-se: P/Q/R em V/F/F, em F/F/V e em F/V/F, se sendo assim, aplicando cada conectivo no final se apenas uma das proposições forem verdadeiras o resultado será: F, F e V.
Logo, se apenas uma das proposições forem verdadeiras o resultado será falso duas vezes e também verdadeiro uma única vez.
Gabarito errado.
Usando o Q=V
(PV¬Q)→(P∧R)=F
(Fv¬V) -> (F^F)=F
(FvF) -> (F^F)=F
F -> F =V
Na condicional:
1- três possibilidades do resultado ser verdadeiro;
2- Quando a primeira proposição for falsa, independente do valor lógico da segunda, o resultado será verdadeiro;
3- apenas um caso de Falso: VF= F
Não concordei com a resposta da questão, pois se atribuírmos valor verdadeiro para a proposição P, o resultado final será falso.
Qual a regra para gabaritar uma questão como essa?

Se tivermos P=V, Q=F, R=F (Resultará em F)

Se tivermos P=F, Q=V, R=F (Resultará em V)

Se tivermos P=F, Q=F, R=V (Resultará em F)

Se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (PV¬Q)→(P∧R) poderá sim ser Falsa, ou seja, estaria a questão correta. Ocorre que ela não seria sempre falsa, ela teria 2 opções para ser falsa e 1 opção onde seria verdade.

Por que o gabarito é a alternativa “Errado”? Alguém poderia ajudar?

Boa sorte a todos!
(PV¬Q)→(P∧R)

SE ATRIBUIRMOS VALORES... 1 TEM QUE SER VERDADE...
P (f)
Q(v)
R(f)
ISSO NÃO FOI ALEATORIO..rsrs..é para provar que com apenas um verdade pode ser que obtenhamos um resultado verdadeiro
VAMOS SUBSTITUIR A PROPOSIÇÃO COM OS VALORES
F v ~V -> F^V Isso é igual a: FvF -> F que dará F-> F que sabemos que no condicional é igual a verdade
GABARITO ERRADO
Se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (PV¬Q)→(P∧R) será falsa.
Sabendo-se da regra que uma condicional pra ser FALSA, a primeira proposição (antecedente) tem de ser Verdadeira e a segunda proposição (consequente) ser Falsa.
P → Q
V → F
   F
1º Possibilidade:
P = V
Q = F
R = F
Para melhor simplificar a explicação considere A como (PV¬Q) e B como (P∧R)

A = (Pv ~Q)
A = (V v V)
A = V

B = (P ^ R)
B = (V ^ F)
B = F

A → B
V → F
    F

2º Possibilidade:

P = F
Q = V
R = F

A = (Pv ~Q)
A = (F v F)
A =     F

B = (P ^ R)
B = (F ^ F)
B        F

A → B
F → F
    V

3º Possibilidade:

P = F
Q = F
R = V

A = (P v ~Q)
A = (F v V)
A =     V

B = (P ^ R)
B = (F ^ V)
B =    F

A → B
V → F
    F

Se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (PV¬Q)→(P∧R) será falsa.
ERRADO!!
NÃO SERÁ FALSO em todas as possibilidades em que apenas uma das proposições seja Verdadeiro, pois tal preposição (PV¬Q)→(P∧R) ADMITE também UMA possibilidade com valor lógico VERDADEIRO.
O comentário do Fábio Dourado esta condizente, mas complicado de entender. Basta construir a tabela verdade:
P Q R (Pv¬Q) (P^R) (Pv¬Q)-->(P^R)
V V V V V V
V V F V F F
V F V V V V
V F F V F F
F V V F F V
F V F F F V
F F V V F F
F F F V F F

Onde estão grifados, são os casos em que apenas uma das proposições serão verdadeiras. Note que nem sempre a conclusão será verdadeira, portanto assertiva falsa
Simplificando!

Se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (PV¬Q)→(P∧R) será falsa.

Escolhi o ( R ) para atribuir o valor verdadeiro.

Se...então ( ----> ) só será falsa quando a primeira proposição for verdadeira e a segunda falsa.
V ----> F = F

( P V ¬Q ) ---> ( P ^ R )
F F F V
F F = verdade
Gabarito: ERRADO.

O comentário do colega Fábio dourado é bem explicativo, vale a pena ler.
A proposição poderá ser Falsa ou Verdadeira.

GAB. ERRADO
De acordo com a tabela-verdade da condicional, temos a seguinte situação onde a mesma é falsa:

V → F

O enunciado nos afirma que se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (P v ¬Q)→(P ^ R) será falsa. Vamos então testar cada situação:

i) P = V e Q, R = F

(P v ¬Q)→(P ^ R) = (V v ¬F)→(V ^ F) = (V v V)→(V ^ F) = V→F = F

ii) Q = V e P, R = F

(P v ¬Q)→(P ^ R) = (F v ¬V)→(F ^ F) = (F v F)→(F ^ F) = F→F = V

iii) R = V e P, Q = F

(P v ¬Q)→(P ^ R) = (F v ¬F)→(F ^ V) = (F v V)→(F ^ V) = V→F = F

Assim, na situação (ii), vemos que se apenas umas das proposições P, Q ou R for verdadeira,
a proposição (P v ¬Q)→(P ^ R) não será falsa.

Resposta: Errado.
Gabarito Errado. Se Q for verdadeiro, a proposição será verdadeira!
Entendi errado o enunciado.
...
mas é o seguinte ...
.
se tiver uma chance de umas das letras ser V e o resultado puder ser V ---> o item está errado.
.
veja:
.
se Q = V --------- ~ Q = F
F v F --> F ^ F -------- (V)
.
ERRADO.
O enunciado está mal escrito, pois vejamos: "Se apenas umas das proposições P, Q ou R for verdadeira, então a proposição (PV¬Q)→(P∧R) será falsa."
.
Ou seja, deixa entender que "basta apenas" 1 CONDIÇÃO (colocando uma preposição V e as outras F) ser Falsa, e então a resposta seria Certo.
E vemos que temos duas possibilidades darão V e uma possibilidade F.
.
Isso daria Gabarito C...
.
Questão fácil de responder mas difícil de entender o que se pede.
1° caso --> Considerando os seguintes valores ( apenas P verdadeiro)

P = V (P v ~Q) --> (P ^ R)

Q = F (~Q = V) V v F --> V ^ F

R = F   V --> F     ( Valor Falso)

2° caso --> Considerando os seguintes valores ( apenas Q verdadeiro)

P = F (P v ~Q) --> (P ^ R)

Q = V (~Q = F) F v F --> F ^ F

R = F   F --> F     ( Valor Verdadeiro)

3° caso --> Considerando os seguintes valores ( apenas R verdadeiro)

P = F (P v ~Q) --> (P ^ R)

Q = F (~Q = V) F v V --> F ^ V

R = V   V --> F     ( Valor Falso)

Dessa forma, concluímos que quando P = F / Q = V / R = F ( 2° caso) a proposição e verdadeira.
Errada
É uma contingência.
apenas umas... PQP! JÁ ANULOU A ESQUESTAO.
Gabarito Errado. Se Q for verdadeiro, a proposição será verdadeira!
GAB E
O ou admite um falso, logo no se então começando com F, a proposição será Verdadeira.

ID

776452

Banca

CESGRANRIO

Órgão

Chesf

Ano

2012

Provas

CESGRANRIO - 2012 - Chesf - Profissional de Nível Superior - Analista de Sistemas

Disciplina

Raciocínio Lógico

Assuntos

Sejam P, Q e R conjuntos não vazios quaisquer para os quais são verdadeiras as seguintes premissas:

premissa 1: P ∩ Q = Ø

premissa 2: Q ⊂ R

Se a notação X indica o complementar do conjunto X, então tem-se que

Alternativas

R ⊂ P

R ∩ Q ≠ Ø

R ∩ P ≠ Ø

Q ∩ P = Ø

P ∩ R ≠ Ø

Comentários

Não é possível visualizar corretamente as operações lógicas.
Enviei um questionamento aos administradores do site.
Nunca vi isso na minha vida.
Não vizualizo a relação entre P e R para responder.
Relembrando:
Dados dois conjuntos A e B, o complementar de B em A, designado por A∖B, é o conjunto cujos elementos são os elementos de A que não pertencem a B:

Ex.

{1,2,3}∖{1,2} = {3};{1,2}∖{1,2,3} = ∅.
Assim, voltando para a nossa questão:

O complementar de P em Q (Q\P), é o próprio conjunto Q, e o complementar de Q em P (P\Q), é o próprio conjunto P, visto que P ∩ Q = Ø.

Ou seja, Q\P = Q e P\Q = P.

Logo:

a) Errado,

Pois se Q ⊂ R, então R não pode estar contido em Q, visto que Q\P = Q.

b) Errado.

Se P\Q = P, então R ∩ P = Ø

c) Correto.

Como Q\P = Q, então R ∩ Q realmente nunca será vazio.

Resposta: Alternativa C.
Hã? Quê?

ID

787591

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2012

Provas

CESGRANRIO - 2012 - Petrobras - Todos os Cargos - Grupo C - Nível Médio I

Disciplina

Raciocínio Lógico

Assuntos

Dadas duas proposições lógicas, p e q, tem-se que a expressão (~p ∨ q) ∧ (~q ∨ p )é logicamente equivalente à expressão

Alternativas

p↔q

p→q

(~p)→(~q)

(p ^ q) ^ ~(p ^ q)

(p ^ q) ^ (~p ^ ~q)

Comentários

P Q ~P ~Q ~P v Q e ~Q v P

V V F F V V V

V F F V F V F

F V V F V F F

F F V V V V V

única que é equivalente é a letra A
Tenho dificuldades em gravar as equivalências... Então, na maioria das vezes perco um pouco de tempo montando a tabela verdade. Que nesse caso a tabela verdade de (~p v q) ^ (~q v p) é igual a tabela verdade de p<->q (se somente se), ou seja dá V F F V. Como o colega David Oliveira fez.
Gab: A

~p v q é equivalente a: ~(~p ) --> q ou seja p -->q (negação da negação resulta em afirmação)

~q v p é equivalente a: ~(~q) --> p ou seja q -->p (negação da negação resulta em afirmação)

Juntando temos: p-->q ^ q-->p que é equivalente a p <--> q

FONTE: GISELE TELES, QCONCURSOS
Equivalências de raciocínio logico que você deve decorar:

P --- > Q = ~Q --- > ~P

P --- > Q = ~P v Q

P < --- > Q = Q < --- > P

P < --- > Q = ~P < --- > ~Q

P < --- > Q = ~Q < --- > ~P

P < --- > Q = (P --- > Q) ^ (Q --- > P)

OBS: Nem precisa negar, apenas substituir.

Alternativa A
Tabela-Verdade da expressão do enunciado:

p q ~p ~q    ~p v q ~q v p    ~p v q ^ ~q v p

v    v f   f v v v

v f   f v f   v f

f     v    v f    v    f   f

f    f v   v v v   v

Tabela-Verdade do P<-->Q (Se e somente se) só admite valores iguais (bicondicional)

p q        P<-->Q

v    v    v

v f        f

f     v       f

f    f      v

Resposta letra A
(~p ∨ q) ∧ (~q ∨ p )é logicamente equivalente à expressão

p↔q. PORTANTO, ALTERNATIVA A.

ID

788737

Banca

CESGRANRIO

Órgão

Transpetro

Ano

2012

Provas

CESGRANRIO - 2012 - Transpetro - Analista de Sistemas Júnior - Infra-Estrutura

Disciplina

Raciocínio Lógico

Assuntos

Considerando os predicados: chefe(x) significando que x é chefe, departamento(x) significando que x é um departamento e chefia (x, y) significando que x chefia y, a restrição “Todo chefe chefia um departamento” pode ser expressa pela seguinte fórmula da lógica de predicados de primeira ordem:

Alternativas

Comentários

GABARITO >>> D

Traduzindo: (1, 2, 3, e 4 são a mesma coisa)

1) "TODO CHEFE CHEFIA UM DEPARTAMENTO"

2) "SE É CHEFE, ENTÃO CHEFIA UM DEPARTAMENTO"

3) "(CHEFE) → (CHEFIA ^ DEPARTAMENTO)"

4) "(CHEFE) → (DEPARTAMENTO ^ CHEFIA)"

Perceba que o gabarito foi o número 3, com uma alteração para o (4), ou seja, "(CHEFE) → (DEPARTAMENTO ^ CHEFIA)", o "DEPARTAMENTO foi invertido com a CHEFIA, mas isso não altera nada, pois o conectivo "^" tanto faz "de frente para trás ou de trás pra frente".

Bons estudos!
entendi foi nada.

ID

788740

Banca

CESGRANRIO

Órgão

Transpetro

Ano

2012

Provas

CESGRANRIO - 2012 - Transpetro - Analista de Sistemas Júnior - Infra-Estrutura

Disciplina

Raciocínio Lógico

Assuntos

Dado que W, Y e Z são proposições no contexto do Cálculo Proposicional, podendo assumir valores falsos ou verdadeiros, conclui-se que

Alternativas

se W é contradição, então Imagem 055.jpg

é tautologia.

se Y é contradição, então Imagem 056.jpg

é tautologia.

se Z é tautologia, então Imagem 057.jpg

é contradição.

se W e Y são contradições, então Imagem 058.jpg

é tautologia.

se W e Y são tautologias e Z contradição, então Imagem 059.jpg

é contradição.

Comentários

Y sendo uma contradição é falso, assim: y -> z, só pode ser uma tautologia, pois para o "então " ser falso, o "y" deveria ser verdadeiro e o "z" falso. Qualquer outra combinação dará resultado verdadeiro (tautologia). Resposta certa letra B.
Na condicional somente sera FALSO (contradição) se a p=V e q=F, se p=F sempre será verdadeiro a condição.

p --> q

V --> F = F

F --> V = V

Y --> Z

F --> V = V
Não entendi as explicações dos colegas, alguém poderia explicar um pouco mais detalhado? Ou poderiam indicar para o professor comentar? Obrigada!
Eu nunca ia acertar uma questão dessa.
Sendo Y uma contradição (ou seja, assumindo apenas o valor falso), para qualquer valor de Z, Y → Z será verdadeiro. Portanto, uma tautologia.
contradição é, em qualquer situação, falso. quando a proposição suficiente de uma inferencia é falsa, independentemente do valor da proposição necessária, esta inferencia será sempre verdadeira.

uma inferencia será falsa somente qiando a proposição sufuciente por verdade e a necessária por falsa.

ID

815266

Banca

AOCP

Órgão

TCE-PA

Ano

2012

Provas

AOCP - 2012 - TCE-PA - Assessor Técnico de Informática - Analista de Segurança

Disciplina

Raciocínio Lógico

Assuntos

Considere as proposições:

p: “Brito pilota aviões";
q: “Brito pilota motos";
r: “Brito pilota carros".

Assinale a alternativa que apresenta uma possível linguagem simbólica para a sentença: “Brito pilota carros e aviões ou Brito não pilota aviões e não pilota motos".

Alternativas

( p ∧ r ) ∨ [(~ p ) ∨ ( ~ q )]

( p ∨ r ) V ~ ( p ∧ q )

( p ∧ r ) V ~ ( p ∨ q )

( p ∧ r ) ∧ ~ ( p ∧ q )

( p ∧ r ) ∨ [( ~ p ) ∧ q )]

Comentários

Gabarito Letra C

Transformando a frase em letras:

Brito pilota carros e aviões ou Brito não pilota aviões e não pilota motos
[ r ^ p ] v [ ~ p ^ ~ q ]

Dessa forma ficaria assim:

[p ^ r] v [~p ^ ~q] ----------------> a segunda premissa é exatamente a negação da disjunção, que pode ser reescrita assim:

[p ^ r] v ~[p v q]

bons estudos
(p ^ r) v (~p ^~q) estaria certo ?
lembrar da equivalencia da negacao da disjuncao
A negação de ^ é v . Sendo assim o correto é ~ (p v q), pois equivalerá a = ~p ^~q.

Gabarito: letra C.
Não entendo a AOCP. Geralmente ela pede a equivalência e dá como certo a negação. A equivalência seria P and R or ~(P and Q)
Alguém sabe explicar pq a letra A não serve?
negação de E ...é OU ( V )
Letra A não serve pois não existe negação que inverta a última porta lógica 'OU, OR, V".

Dá pra se chegar à resposta por eliminação, mas a banca forçou a barra pois a resposta é um equivalência lógica, não uma leitura direta por símbolos (simbólica).
Não esquecer de negar o ^ dentro dos parênteses.

Negação de ^ é Ou
O problema dessa questão, na verdade não é nem a questão em si, mas sim o anunciado. O anunciado diz" Leitura por simbolos". Sendo que a resposta é um equivalência lógica, não uma leitura direta por símbolos (simbólica).
Uma coisa é pedir equivalência outra é pedir apresentação em forma de símbolos!! tnc kkk
Larissa Almeida
A Letra A não serve pelo seguinte motivo:

( p ∧ r ) ∨ [(~ p ) ∨ ( ~ q )]

O conectivo da questão deve ser o E ( Brito não pilota aviões e não pilota motos). No caso desta assertiva como as negações estão entre parênteses não irão alterar o sinal da preposição, que continuará sendo OU, o que torna a assertiva errada.
Espero que tenha entendido.

ID

818260

Banca

Exército

Órgão

EsFCEx

Ano

2011

Provas

Exército - 2011 - EsFCEx - Oficial - Magistério Matemática

Disciplina

Raciocínio Lógico

Assuntos

Analise as afirmativas a seguir, colocando entre parênteses a letra “ V" quando se tratar de proposição verdadeira e a letra “F" quando se tratar de proposição falsa. A seguir, assinale a alternativa que indica a sequência correta.

( ) É primo, todo número α tal que α = n² + n + 41 onde n ∈ IΝ.

( ) Dados três inteiros consecutivos, um deles é múltiplo de 3.

( ) Se x e y são inteiros não nulos, então mmc(x,y) . mdc(x,y) = |xy|

( ) Para todo inteiro positivo t tem-se que 4 ^t ≡ 1 + 3t (mod9).

Alternativas

F – V – V – V

F – F – V – V

F – V – F – V

V – F – V – F

V – V – F – F

Comentários

Dados três inteiros consecutivos, um deles é múltiplo de 3.

Por que não poderia ser -1, 0, +1; 0, 1, 2; ou -2, -1, 0?????

ID

818269

Banca

Exército

Órgão

EsFCEx

Ano

2011

Provas

Exército - 2011 - EsFCEx - Oficial - Magistério Matemática

Disciplina

Raciocínio Lógico

Assuntos

Sejam as afirmações sobre Lógica Matemática:

I. considere a, b e c proposições simples e o valor lógico da proposição
A : a → b é verdadeiro. Então, os valores lógicos das proposições compostas B : (a∧c) → (b ∧ c) e C: (a V c) → (b V c) são verdadeiro e falso, respectivamente.

II. é válido o argumento: “Todo número primo é ímpar e nenhum número ímpar é par. Portanto, existe um número primo que é par”.

III. considerando A = {1,2,3} e B = [ - 1,1 ] então a proposição ∃x ∈ A, ∃ y ∈ B;|x-y| = 2/3 é verdadeira.

IV. sejam p e q proposições simples então P:~ (p → q) ∧ [ ( ~ p ∧ q ) V ~(p V q)] é uma contradição.

Assinale a alternativa correta:

Alternativas

somente II está correta

somente I e II estão corretas

somente III e IV estão corretas

somente I, II e III estão corretas

somente I, III e IV estão corretas

Comentários

Gab. C

???
questão para Mestre de matemática

ID

818278

Banca

Exército

Órgão

EsFCEx

Ano

2011

Provas

Exército - 2011 - EsFCEx - Oficial - Magistério Matemática

Disciplina

Raciocínio Lógico

Assuntos

Analise as afirmativas a seguir, colocando entre parênteses a letra “V” quando se tratar de proposição verdadeira e a letra “F” quando se tratar de proposição falsa. A seguir, assinale a alternativa que indica a sequência correta.

( ) A relação R sobre R definida por xRy ⇔ x ≤ y é não anti-simétrica.

( ) A aplicação: ƒ: N x N → N; ƒ(x,y) = xy pode ser estendida aos racionais.

( ) A função g: N → Q tal que g(n) = 2n tem lim g(n) ≠ 0.
(n+1)! ^n→+∞( ) Se h: [α,b] → R é derivável, ∃c ∈ (a,b) ; h(b) - h(a) = h'(c) (b - a).

Alternativas

F – V – V – F

V – V – F – F

F – F – V – V

F – F – F – V

V – F – V – V

Comentários

Gab. D

???

ID

829690

Banca

CESGRANRIO

Órgão

Innova

Ano

2012

Provas

CESGRANRIO - 2012 - Innova - Analista de Sistemas Júnior

Disciplina

Raciocínio Lógico

Assuntos

Na avaliação de um computador, foram feitos testes exaustivos da taxa de falhas nas operações de acesso à memória. Seja p uma proposição representando que um acesso à memória foi bem sucedido, e q, uma proposição representando que houve sobrecarga de tensão. Foi constatado nos testes que, em todas as situações em que o acesso à memória falhou, houve sobrecarga de tensão, fato que pode ser representado pela fórmula ¬ p → q da lógica proposicional. Em um novo teste, constatou-se que não houve sobrecarga de tensão. Sobre esse novo teste, e considerando-se os resultados obtidos nos testes anteriores, pode-se deduzir que

Alternativas

¬ p

p ^ q

¬ p ^ ¬ q

Comentários

como nao houve sobrecarga então subtende-se que o resultado foi p
Eu encontrei como resposta a letra E. Fazendo ~(~p -> q)... Por que este não é o gabarito?
todas as situações em que o acesso à memória falhou, houve sobrecarga de tensão...

Se ao final ele diz que não houve sobre carga de tensão, logo, deduz-se que a memória não falhou

E memoria não falhar = memoria bem sucedida = P
Vamos primeiro organizar os dados da questão:

p: Acesso à memória foi bem sucedido

q: Houve sobrecarga de tensão

A questão também informa que foi constatado nos testes que, em todas as situações em que o acesso à memória falhou, houve sobrecarga de tensão, fato que pode ser representado pela fórmula ¬ p → q da lógica proposicional.

O que a questão realmente quer saber é o que aconteceu com o acesso á memória no novo teste. Nesse caso não é possível negar a proposição composta ¬ p → q, pois a única informação que foi passada é que não houve sobrecarga de tensão.

¬ p → q é equivalente a ¬ q → p

Sendo ¬ q representando que não houve sobre carga de tensão. Ou seja, se não há sobrecarga de tensão o acesso a memória é bem sucedido, representada por p. Por isso gabarito letra "b"
Tanto pela negação como pela equivalência podemos encontrar a resposta.

Temos a seguinte preposição na questão: ~P->Q. Como quero ~Q, podemos negar ou ir pela equivalência, vejamos

NEGAÇÃO: P ^ ~Q

EQUIVALÊNCIA: ~Q ->P ou P v Q (essa não vale, pois queremos é ~Q)

Daí vamos às alternativas

a)q (Nas análises até encontramos o Q, mas queremos é o ~Q - item ERRADO)

b)p (Nas análises encontramos P - item CERTO)

c)¬ p (Nas análises encontramos P - item ERRADO)

d)p ^ q (Nas análises encontramos a proposição P ^ ~Q - item ERRADO)

e)¬ p ^ ¬ q (Nas análises encontramos a proposição P ^ ~Q - item ERRADO)

GABARITO: B
P: Bem sucedido

Q: Houve sobrecarga de tensão

Premissa 1 : ¬ p → q

Premissa 2: ¬ q    Em um novo teste, constatou-se que não houve sobrecarga de tensão ( por isso ¬ q na premissa 2 )

Conclusão: ? A conclusão é o que se pede no comando da questão.

Considerando que as premissas são verdadeiras, chegamos a que:

¬ q = V por consequência q = F

¬ p = F por consequência p = V (Conclusão)

Premissa 1 : ¬ p → q _F__→ _F_ = (V)   para que essa premissa seja verdadeira ¬ p tem que ser falso.

Premissa 2: ¬ q (V)

Conclusão: p

acho q é isso..espero ter ajudado!!!

abs

ID

829693

Banca

CESGRANRIO

Órgão

Innova

Ano

2012

Provas

CESGRANRIO - 2012 - Innova - Analista de Sistemas Júnior

Disciplina

Raciocínio Lógico

Assuntos

A lógica de predicados de primeira ordem foi escolhida para representar um conjunto de restrições que um modelo de dados deve satisfazer para adequar-se a um novo sistema. Considere os predicados P(v), representando que v é um pedido, I(w) representando que w é um item, e C(v,w) representando que w consta em v,para quaisquer variáveis v e w.

Qual a fórmula que pode ser usada para representar que, em qualquer pedido, consta ao menos um item?

Alternativas

∀ x ∀(P(x)∧ι(y)∧C(x,y)

∃x∃yP(x)∧ι(y)∧C(x,Y))

∀x(P(x) -> ∀y(ι(y) C(x,y)))

∀(P(x) -> ∃y(ι(y)∧C(x,y)))

∃x(P(x)∧∀y(ι(y) C(x,y)))

Comentários

Vai pela lógica...

Para todo e qualquer = A virado de cabeça para baixo...

Existe pelo menos um = E virado para a esquerda...

Só achar a opção que contenha a sequencia... A ao contrario p(v) seguido de E ao contrário... :D
Resolve analisando o comando da questão que fica bem mais fácil.

"Em qualquer pedido, consta ao menos um item".

• "Em qualquer pedido": mesma coisa que falar em TODO pedido (já sabe que vai ter que ter um A invertido na resposta).

• "...ao menos um...": mesma coisa que falar em ALGUM item (já sabe que vai ter que tem um E invertido na resposta).

Depois, o negócio é traduzir o que ele pede:

∀(P(x) ∃y(ι(y)∧C(x,y)))

Para todo modelo de informações de dados, pelo menos um item vai constar no pedido.

ID

829696

Banca

CESGRANRIO

Órgão

Innova

Ano

2012

Provas

CESGRANRIO - 2012 - Innova - Analista de Sistemas Júnior

Disciplina

Raciocínio Lógico

Assuntos

Considere que três fatos acerca de situações pertinentes ao domínio de um sistema são representados pelas proposições p, q e r da lógica proposicional. Para que o módulo A desse sistema seja executado, basta que aconteçam ambos os fatos p e q simultaneamente. Por sua vez, para que o módulo B seja executado, é suficiente que um entre os fatos q e r aconteça. Uma situação na qual, certamente, ambos os módulos são executados, está representada por

Alternativas

(p ˅ q) ˅r

(p ˅ q) ˄r

(p ˄ q) ˅r

p ˄(q ˅r)

p ˄(q ˄r)

Comentários

Alguém pode explicar ?
Vamos fazer por exclusao

a) (p ˅ q) ˅ r. Entre p ˅ q, pode ser p. p ˅ r, pode ser r logo, nao acontece A nem B

b) (p ˅ q) ˄ r. Entre p ˅ q, pode ser p. p ˄ r, tambem nao acontece A

c) (p ˄ q) ˅r. Entre p ˄ q, acontece os 2, mas quando tem ˅r, pode ser apenas r. nao acontece A nem B

d) p ˄(q ˅r). Entre q ˅r, pode acontecer r. p ˄ r, nao acontece A

e) p ˄(q ˄r). Aqui acontecem os 3 logo, acontece A e B
Minha conclusão foi a seguinte: A= P^Q B= Q^R ... nesse caso pra dá A e B foi a letra E. P ou (Q ou R)
Segue a explicação:

Vou representar V como 1 e F como 0.

Se temos 3 proposições, logo temos 2^3 possibilidades de entradas nesse sistema,

p q r

1 1 1

1 1 0

1 0 1

1 0 0

0 1 1

0 1 0

0 0 1

0 0 0

A partir das 3 entradas temos as condições: para ligar o Mod A (p ^ q) e para ligar o Mod B (q v r)

p q r p ^ q q v r

1 1 1 1 1

1 1 0 1 1

1 0 1 0 1

1 0 0 0 0

0 1 1 0 1

0 1 0 0 1

0 0 1 0 1

0 0 0 0 0

A partir daí, foi dito que se quer acionar todo o sistema, então temos que acionar o Mod A e o Mod B, ou seja, um e (^) outro.

p q r p ^ q q v r (p ^ q) ^ (q v r)

1 1 1 1 1 1

1 1 0 1 1 1

1 0 1 0 1 0

1 0 0 0 0 0

0 1 1 0 1 0

0 1 0 0 1 0

0 0 1 0 1 0

0 0 0 0 0 0

Observem que só temos duas possiblidades de "ligar" esse sistema:

p q r p ^ q q v r (p ^ q) ^ (q v r)

1 1 1 1 1 1

1 1 0 1 1 1

Quando p, q e r estão "ligados" ou quando p e q estão "ligados" e r "desligado".

Assim p ˄(q ˄r) liga o sistema, pois 1 ^ (1 ^ 1) = 1 (sistema ligado)

p q r p ^ q q v r (p ^ q) ^ (q v r)

1 1 1 1 1 1

p ˄(q ˅r) não há garantia que o sistema será ligado

p q r p ^ q q v r (p ^ q) ^ (q v r)

1 1 1 1 1 1

1 1 0 1 1 1

1 0 1 0 1 0

E assim por diante...

Detalhe: se somente p e q estão "ligados" já é o suficiente para o sistema funcionar, independemente do estado r (vide segunda combinação da tabela verdade completa). Mas não temos essa alternativa como resposta. Então, das respostas possíveis apresentadas, a alternativa E é a única que liga o sistema.

ID

868450

Banca

CESPE / CEBRASPE

Órgão

TRE-MS

Ano

2013

Provas

CESPE - 2013 - TRE-MS - Analista Judiciário - Análise de Sistemas

Disciplina

Raciocínio Lógico

Assuntos

Considere a seguinte sentença: O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas, da mesma forma, o caráter do homem é forjado pelas dificuldades que ele passa. Se P, Q e R são proposições simples e convenientemente escolhidas, essa sentença pode ser representada, simbolicamente, por

Alternativas

Comentários

Bom, eu fui por eliminação. Entendi que o "se, e somente se" seria o que mais se aproximaria de "da mesma forma".
Concordo com o Luka.

Nunca fiz uma prova que a Bicondicional (se, e somente se) fosse descrito desta maneira. (da mesma forma)

Gabarito A
Eu fiz pelo E ( ^ ) e depois pela bicondicional < -- >
Eu fui por eliminação.A única certeza que eu tinha era que a proposição deveria conter o conectivo " e " (^)

e que são 3 proposições:

P: O vinho é produzido pelo pisar das uvas
Q:o caráter do homem é forjado pelas dificuldades que ele passa
R: o azeite é obtido pelo prensar das azeitonas

P ^R corresponde a :O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas

então procurei dentre as alternativas

aquela que tivesse o conectivo " e" ( ^ ) e as 3 proposições, e então encontrei a alternativa "A" :D

Não poderia ser a alternativa D pois não tenho o conectivo ou (v) na frase
Pessoal, uma bicondicional é um termo usado em lógica proposicional que significa "se e somente se" ,ou seja, A implica em B como B implica em A. Como na questão temos "da mesma forma", logo podemos deduzir que a proposição P^Q implica em R, ou vice versa, sendo representada então por (P^Q)<-->R.Uma confusão que poderia haver mas que não consta no rol das opções seria confundir "da mesma forma" com o conectivo --->,ou seja,representa-la por
(P^Q)-->,este conectivo expressa uma implicação, ou condicional é a indicação do tipo "SE...ENTÃO", indicando que uma condição deve ser satisfeita necessariamente para que a outra seja verdadeira. Por exemplo, a expressão: "Se João esquia, Maria nada" é uma implicação. Logo, não há dúvida que a alternativa correta é a "A".

Avante!!!!!!!!!
Como se tem 3 proposições de cara já podem ser eliminadas as letras b e c, que apresentam apenas 2 proposições.
A partir dai é só se lembrar a nomenclatura de cada termo ^ = e (mas, embora), v = ou, ->= se... então, <-> se e somente se(da mesma forma)
Como o CESPE está inovando heim? Está pegando termos sinônimos. Ou seja, conjunções para deixarmos a ver navios. Mas para isso tem o site: "questões de concuros", para nos deixar apto a essas mudanças/ inovações da banca. Bons Estudos!
O símbolo ⇒ tautologia (implicação lógica) "da mesma forma"
O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas, da mesma forma, o caráter do homem é forjado pelas dificuldades que ele passa.

da mesma forma = se, e somente se
Pessoal, alguém pode esclarecer a diferença da forma de representação dos símbolos de equivalencia e bicondicional? O símbolo utilizado na questão parece mais com equivalência.
Perfeita a observação da Alessandra. O sinal utilizado na letra A não é o da bicondicional ( <-->), mas sim o sinal de equivalência. O sinal <--> é "se e somente se". Já o sinal <=> é de equivalência. Note que há uma diferença nas "setas", onde uma é seta simples e outra é seta dupla.
Assim, na equivalência de proposições, podemos dizer que "se corro então nado" é equivalente a "não corro ou nado", que simbolicamente seria A --> B <=> ~A v B.
Na questão, o 'da mesma forma", funciona como equivalência. Assim, dizer que o vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas é o mesmo que (é equivalente) dizer que o caráter do homem é forjado pelas dificuldades que ele passa.
Resumindo, na letra A o sinal <=> não é da bicondicional, mas sim de equivalência.
Fonte: Professor Brunno Lima (aula do site: euvoupassar.com.br)
Essas questões do CESPE de múltipla escolha me fazem ter pesadelos... que saudades das questões C ou E :(
A princípio, fiquei sem saber o que responder, porque, como a maioria aqui, confundi o símbolo da bicondicional com o da equivalência. No entanto, após perceber que era o símbolo da equivalência, é possível chegar facilmente à conclusão de que "da mesma forma" significa equivalência. Portanto, temos a conjunção "P e Q" equivalente a R.
Os comentários dos colegas sobre bicondicional podem confundir quem ainda está começando a matéria. E o comentário com mais votos está errado. Por favor, curtam o comentário do colega ortiz_rj que é o único correto e com a melhor explicação.
Acho forçar a barra considerar "da mesma forma" = se somente se ... Blza que em múltipla escolha dava pra marcar a correta por eliminação.
Se fosse de C ou E teria errado fácil, pois pensei mais lógico considerar P^Q^R.
Complicado ....
Observa-se que na proposição P: “O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas, da mesma forma, o caráter do homem é forjado pelas dificuldades que ele passa.”, existe uma conjunção “e”.

O trecho “da mesma forma”, dá o sentido claro de uma bicondicional, onde “O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas...”, é uma Hipótese (ou antecedente) e “...o caráter do homem é forjado pelas dificuldades que ele passa.”, é uma conclusão (ou consequente).

Sendo assim, podemos reescrever a proposição como: (P ^ R) ←→ Q.

RESPOSTA: (A)
DÚVIDA:
Houve a inversão das proposições R e Q por que é uma regra? Ou nao precisaria usar as letras na ordem dada pela questão (P, Q e R)?
P: O vinho é produzido pelo pisar das uvas
Q:o caráter do homem é forjado pelas dificuldades que ele passa
R: o azeite é obtido pelo prensar das azeitonas

P ^R corresponde a :O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas
...
(P^Q) < = > R
Sinônimos da bicondicional : "da mesma forma" , "tal e qual" , "tanto quanto", "assim como"
Chutei muito nessa questão e só chutei porque não era de C ou E, pois, pra mim, nenhuma das alternativas tinha a resposta. Nunca vi, nem em questões, nem professores dizendo que o tremo "da mesma forma que" pode ser trocado pelo "se somente se".
Boa essa questão!! o CESPE testa a todo momento sua capacidade de pensamento!! Meu Deus que banca abençoada...

A letra A está conforme a montagem da proposição somente as letras não estão necessariamente na ordem!
Vi nos comentários, inclusive no do professor que o símbolo da resposta é bicondicional, no entanto, concordo e acho mais lógico o que alguns colegas comentaram, de ser equivalência. E agora? alguém pode confirmar se é bicondicional ou equivalência?
Embora o símbolo da questão NÃO ser o da bicondicional (<->), mas sim, o símbolo de EQUIVALÊNCIA LÓGICA, para a CESPE:

(Q313206 ) "Considere que as proposições sejam representadas por letras maiúsculas e que se utilizem os seguintes símbolos para os conectivos lógicos: ∧ – conjunção; ∨ – disjunção; ⇒ – condicional; ⇔ – bicondicional [...] "
Não faz sentido algum ser bicondicional, voto com os colegas que isso é uma equivalência , para ser bicondicional seria o mesmo que dizer assim

O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas, da mesma forma, o caráter do homem é forjado pelas dificuldades que ele passa.

O vinho ser produzido pelo pisar das uvas e o azeite ser obtido pelo prensar das azeitonas, É CONDIÇÃO SUFICIENTE E NECESSÁRIA PARA O caráter do homem ser forjado pelas dificuldades que ele passa.

Faz algum sentido? Uma coisa depende da outra?

Isso é uma equivalência, uma metáfora, algo utilizado para remeter a outra coisa, com sentido equivalente

Obs: apesar disso, não sei se a intenção da banca foi essa (equivalência) pois o sinal da condicional na letra C e E estão com as setinhas grossas também...
Essa eu acertei por exclusão..

Pra mim a resposta seria P ^ Q ^ R
Eu teria marcado P ^ Q ^ R. Não tinha, fui na menos ruim e acertei. Mas não entendi com clareza.
"da mesma forma" dá ideis de "se e somente se"? Já anotei... Cespe não é brinquedo viu... Essa banca impressiona
P: O vinho é produzido pelo pisar das uvas
Q:o caráter do homem é forjado pelas dificuldades que ele passa
R: o azeite é obtido pelo prensar das azeitonas

P ^R corresponde a :O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas

...

(P^Q) < = > R
GABARITO: A
Bem sem noção ou o que equivale ao jeito Cespe. Se e somente se <===> para representar "o caráter do homem é forjado pelas dificuldades que ele passa". Esses avaliadores deveriam parar com as drogas.
Porque é invertida as posições de Q e R ?
Dão ideia de se e somente se:
Da mesma forma
Assim como
GABARITO A

>> É a segunda questão que eu vejo do Cespe em que trata o SE, SOMENTE SE como ''EQUIVALENTE A ALGO'' ''IGUAL A ALGO'' '' DA MESMA FORMA QUE''
A expressão “da mesma forma” indica a estrutura bicondicional (...SE E SOMENTE SE...)

São expressões sinônimas do “...SE E SOMENTE SE...”:
...da mesma forma...
... do mesmo modo...
... tal e qual...
... tanto quanto...

Temos que
- "O vinho é produzido pelo pisar das uvas" = P
- "e" = ^
- "o azeite é obtido pelo prensar das azeitonas" = R
- "da mesma forma" <-->
- "o caráter do homem é forjado pelas dificuldades que ele passa" = Q
P ^ R <--> Q

Gabarito letra A
Questão
Considere a seguinte sentença: O vinho é produzido pelo pisar das uvas e o azeite é obtido pelo prensar das azeitonas, da mesma forma, o caráter do homem é forjado pelas dificuldades que ele passa. Se P, Q e R são proposições simples e convenientemente escolhidas, essa sentença pode ser representada, simbolicamente, por

P "Considere a seguinte sentença: O vinho é produzido pelo pisar das uvas"
R "o azeite é obtido pelo prensar das azeitonas"
Q "o caráter do homem é forjado pelas dificuldades que ele passa"

"e" representado por ^ (conjunção)
"da mesma forma" representado por ↔ (bicondicional)

Expressões sinônimas do "...SE E SOMENTE SE..."
- Da mesma forma;
- Do mesmo modo;
- Tal e qual;
- Tanto quanto.
Gabarito letra A ✅

ID

868453

Banca

CESPE / CEBRASPE

Órgão

TRE-MS

Ano

2013

Provas

CESPE - 2013 - TRE-MS - Analista Judiciário - Análise de Sistemas

Disciplina

Raciocínio Lógico

Assuntos

Considere a seguinte sentença: A beleza e o vigor são companheiras da mocidade, e a nobreza e a sabedoria são irmãs dos dias de maturidade. Se P, Q e R são proposições simples e convenientemente escolhidas, essa sentença pode ser representada, simbolicamente, por

Alternativas

Comentários

Não há relação disjuntiva nem condicional entre as 2 proposições, sendos estas conjuntivas. O mais difícil da questão é ver que são apenas 2 proposições
Concordo com o colega acima,o dificil da questão é identificar que são apenas 2 proposições

P : A beleza e o vigor são companheiras da mocidade
R:a nobreza e a sabedoria são irmãs dos dias de maturidade

Observe que são 2 sujeitos mas apenas um predicado,o que configura uma preposição simples

O que liga as proposições é o conectivo "E" (^)

Portanto podemos representá-la da seguinte forma:

P ^ R

Alternativa : D
ALTERNATIVA "D"

Entendo da seguinte forma, no período correspondente, temos duas orações, que são representadas por duas proposições simples, que ligadas ao conectivo (^) formam uma proposição composta:
1ª - A beleza e o vigor são companheiras da mocidade, e (^)
2ª - a nobreza e a sabedoria são irmãs dos dias de maturidade.
Notem que para cada oração destacada há apenas um verbo, logo, teremos duas proposições simples. Simbolicamente representada por:
OBS: No período, não importa se o sujeito é simples ou composto, para reconhecermos quantas proposição simples há dentro desse período, basta separarmos as orações por meio dos verbos.
Importante lembrar!!! Proposição é uma declaração/afirmação que admite um atributo (V ou F).

Bons estudos...
Nossa colega michelle pacheco está correta. O comentário postado por gabriela segue incorreto. Não considera o sujeito da oração e sim o verbo. Após questionar a concurseira michelle ela apresentou referências em sites a minha pessoa comprovando que realmente a mesma apresentou argumentos corretos. Perfeito seu comentário!!!!
Avante!!!!!!
Fiquei com uma duvida depois do comentario de Frederico Brito, onde eu interpretei que para distiguir as preposições tem que ver o verbo. E se houver uma questão com varios verbos?

Ex: Maria correndo e pulando vai à casa da vovo, e João sorrindo e cantando vai à casa do vovô.

E aí ? Alguem poderia explicar.

Grata.
E eu consegui visualizar P e R, mas o enunciado pede o Q!
Alguém pode comentar isso? acaso podemos ignorar uma
sugestão do enunciado?
Olá Raquel, tomei a liberdade de responder sua dúvida.
Bem, com relação à identificação dos verbos, é preciso cuidado/cautela ao analisar o item, isso porque já vi o Cespe cobrando questões de forma técnica/conceitual e até mesmo interpretativa, causando um certa confusão. Mas, quanto ao exemplo trazido, temos:
Ex: Maria correndo e pulando vai à casa da vovó, e João sorrindo e cantando vai à casa do vovô.
Simbolicamente poderíamos representá-la (P ^ Q), sendo:
P = Maria correndo e pulando vai à casa da vovó, ----- Suj. Simples (Maria); correndo e pulando (formas nominais do verbos "correr x pular" - gerúndio); verbo principal (ir)
e = conjunção
Q = João sorrindo e cantando vai à casa do vovô. ----- Suj. Simples (João); correndo e cantando (formas nominais dos verbos "correr x pular" - gerúndio); verbo principal (ir)
Espero ter ajudado, bons estudos...
SÓ HÁ 2 PROPOSIÇÕES SIMPLES QUE SE LIGAM COM A CONJUNÇÃO ''E''... NÃO VEJO A TERCEIRA.

GABARITO ''D''
Muito bom MIchelle!
É só contar os verbos, só há dois verbos ("são")
MOLE, MOLE, GALERA!!!

Eu fiz diferente, alcançando o mesmo resultado:

(P ^ Q) ^ (R ^ S)

P ^ R

Temos um antecedente E um consequente.

Logo, P ^ R, em que P representa 2 proposições simples (P ^ Q) e R representa 2 proposições simples (R ^ S).

* GABARITO: LETRA "D".

Abçs.
Duas proposições simples conectadas pela conjunção.

Letra D
Tá engraçadinha essa Cespe.
A sentença:"A beleza e o vigor são companheiras da mocidade, E a nobreza e a sabedoria são irmãs dos dias de maturidade." é uma conjunção, onde pode ser corretamente separada como:

P = A beleza e o vigor são companheiras da mocidade

Q = a nobreza e a sabedoria são irmãs dos dias de maturidade.

Assim temos:

P ^ Q = "A beleza e o vigor são companheiras da mocidade, E a nobreza e a sabedoria são irmãs dos dias de maturidade."

Resposta: Alternativa D.
CUNVEEEEEEEEEEESAA!!!!!
CESPE "trollando" com a terceira proposição. Banca mítica!
Essa Cespe já é jaguara, querendo colocar proposição aonde não tem
Admiro-me não ser P, Q, R e S. Porque com P, Q e R dá pra ver que tem alguma coisa errada.
Duas proposições simples conectadas pela conjunção.

Letra D
eles tentar confundir com algo fácil
Não colocou RESPECTIVAMENTE, resolveram usar:
P= A beleza e o vigor são companheiras da mocidade, E(^) R= a nobreza e a sabedoria são irmãs dos dias de maturidade
Alternativa A) P^R
✅Gabarito Letra D.
P^R
- Cespe tentando fazer pegadinha colocando mais de uma proposição.
A beleza e o vigor são companheiras da mocidade, E a nobreza e a sabedoria são irmãs dos dias de maturidade
Bons estudos!
poderia ser Q^R ( se tivesse no gabarito) ou P^R. Vamos separar as informações da sentença em análise: “A beleza e o vigor são companheiras da mocidade, e a nobreza e a sabedoria são irmãs dos dias de maturidade”.
Observe atentamente a expressão “A beleza e o vigor são companheiras da mocidade”. Este "e" que liga os
elementos (beleza, vigor) não é o conectivo conjunção, pois o predicado “companheiras da mocidade” é
único, de modo que essa proposição toda é simples. O mesmo se aplica à expressão “a nobreza e a sabedoria
são irmãs dos dias de maturidade”, por isso temos apenas duas proposições simples ligadas pelo conectivo
conjunção.
Podemos, convenientemente, escrever as expressões do seguinte modo:
P: A beleza e o vigor são companheiras da mocidade.
R: A nobreza e a sabedoria são irmãs dos dias de maturidade.
Sendo assim, a sentença "A beleza e o vigor são companheiras da mocidade, e a nobreza e a sabedoria são
irmãs dos dias de maturidade" pode ser representada por P ∧ R.

Fonte: estratégia concursos.
Li vários comentários e não achei nenhum lugar em vários documentos que tenho para estudo, explicando porque a segunda preposição passa a ser chamada de "R".
Ainda acho q é o simples P ^ Q
Se P, Q e R são proposições simples e convenientemente escolhidas.

Por esse motivo a proposição recebeu o nome R, como poderia ser Q.

ID

901963

Banca

VUNESP

Órgão

PC-SP

Ano

2013

Provas

VUNESP - 2013 - PC-SP - Investigador de Polícia

Disciplina

Raciocínio Lógico

Assuntos

Considerando os conectivos usuais de negação, disjunção (inclusiva), conjunção e implicação (material), assinale a alternativa correta.

Alternativas

Não existem tautologias só com o conectivo de implicação.

Não existem tautologias com o conectivo de conjunção.

Não existem contradições sem que ocorra o conectivo de negação.

Não existem contradições com apenas uma letra sentencial (considerando que ela pode ser utilizada mais de uma vez).

Existem tautologias que só possuem os conectivos de disjunção e conjunção.

Comentários

x	y	x^y	x v y	x=>y	~x	~y	~x v ~y	y=>(x=>y)	(~x v ~y) ^ (y=>(x=>y)	x ^ ~x
v	v	v	v	v	f	f	v	v	v	f
v	f	f	v	f	f	v	v	v	v	f
f	v	f	v	v	v	f	v	v	v	f
f	f	f	f	v	v	v	v	v	v	f

resolvendo a tabela verdade, resolve-se a questão!
bem trabalhosa...

Questãozinha chata!
Se vc se contradiz, vc é e não é algo ao mesmo tempo, então não há como haver uma contradição sem uma negação.
São contradições: A então não A; A e não A.
Para mim a letra "E' também está correta
Neste exemplo:
(A ^ B) u (A u ~A) é uma tautologia e só possui os conectivos de disjunção e conjunção
Letra C de Com certeza vocÊ terá que estudar muito, nessa eles pegaram mais pesado...
E) Existem tautologias que só possuem os conectivos de disjunção e conjunção: (v) e (^)

(A ^ B) v (¬A)v(¬B)
Nesse caso a banca considerou a negação como conectivo e deixou isso bem claro na questão .
É o tipo de questão que deve ser lida algumas vezes , então é melhor deixar para o final da prova .
Renato...e se tivermos X, Y e Z?
A LETRA "E" NÃO ESTA CORRETA POIS A BANCA CONSIDEROU O MODIFICADOR LÓGICO COMO CONECTIVO.
Depois de errar e refletir, percebi o que o examinador quis dizer... Na verdade, de que forma ele quis confundir o candidato: Citou que uma tautologia pode ser composta apenas pelos conectivos, sendo que, sem elementos, não há tautologia!!!! Elementos são o "cerne" da proposição
COMENTÁRIO:

Para resolver essa questão, desenha-se a tabela verdade e aplica-se um contra exemplo a cada alternativa, até encontrarmos a verdadeira, assim:

a) Alternativa falsa, pois encontramos um contra exemplo que contradiz a afirmação.

b) Alternativa falsa, pois encontramos um contra exemplo que contradiz a afirmação.

c) Alternativa correta, pois pela definição, Contradição é toda proposição cujo valor lógico não é tautológico. Singelamente, é possível afirmar que a contradição consiste na afirmação e negação simultâneas de uma mesma coisa, na mesma decisão.

Letra C.
Tipo de questão que deve-se prestar atenção no enunciado.
Letra E, está errada pois o examinador deixou claro que negação tbm deve ser considerado conectivo.
Sendo assim, não existem Tautologias sem negação. Letra C !
c) Não existem contradições sem que ocorra o conectivo de negação.
Descordo pois (P <-> Q) <-> (P v Q)
Não tem negação e é contradição
Não é?
EXEMPLOS QUE SE ELIMINA, DE PRIMEIRA, A LETRA E:
Pv(~P)
P->P
P<->P
Pv(~P)

TODOS ESSES EXEMPLOS GERAM UMA TAUTOLOGIA

FÉ EM DEUS E BONS ESTUDOS!
c) Alternativa correta, pois pela definição, Contradição é toda proposição cujo valor lógico não é tautológico. Singelamente, é possível afirmar que a contradição consiste na afirmação e negação simultâneas de uma mesma coisa, na mesma decisão.
Como se resolve isso no papel? Tem que inventar as formulas ate achar alguma que elimine a alternativa? kkkk
CONSIDERE = VUNESP solicitou SOMENTE (E, OU e SE...ENTÃO) para está questão especificamente.

==================================================================================================

os operadores lógicos : (se...e somente se) e o (ou exclusivo) não foram considerados,pela VUNESP, nesta questão conoforme enunciado. " Considerando os conectivos usuais de negação, disjunção (inclusiva), conjunção e implicação (material)"

==================================================================================================

Montando a seguinte tabela:

============================================================================================================

P Q E OU SE... ENTÃO

V V V V V

V F F V F

F V F V V

F F F F V

Logo,

c) Não existem contradições..........sem que.......ocorra o conectivo de negação.

não existe falso..................sem que.......ocorra uma falsidade.

apenas a linha V V que sempre teve como resultado V
Pessoal, não é válida a proposição composta (p<->q)^(p v q), pois o enunciado disse:
"Considerando os conectivos usuais de negação, disjunção (INCLUSIVA), conjunção e implicação (material), assinale a alternativa correta."
  (p q) ^ (p v q)

P Q    (p<---> q) (p v q) (p<--> q) ^ (p v q)

V V V F F

V F F V   F

F V F V    F

F F V F   F

Ícki Φ ,você não esta usando uma disjunção inclusiva ( V ) conforme o enunciado pede e sim uma disjunção EXCLUSIVA ( v ).

Nosso colega Gaio Quaresma está correto.
Sacanagem pedirem 50% de aproveitamento em cada matéria no concurso da policia civl SP/2018. Principamente em raciocinio lógico, uma vez que tal disciplina não se mostra essencial para a carreira policial, bem como não avalia a inteligência do candidato.
A) Não existem tautologias só com o conectivo de implicação.

Realmente, existem tautologias com outros conectivos tbm.
#interpretação
Pode dar essa ideia tbm né , o "só"? Ou to enganada...
Vejamos cada alternativa:

a) Não existem tautologias só com o conectivo de implicação.
ERRADO. A condicional p-->p é uma tautologia.

b) Não existem tautologias com o conectivo de conjunção.
ERRADO. A proposição abaixo tem o conectivo conjunção, e é uma tautologia: (p e p) --> p.

c) Não existem contradições sem que ocorra o conectivo de negação.
CORRETO. Repare que sempre que escrevemos uma contradição, ela contém a negação: “p e ~p”, “p se e somente se ~p” etc. Alguns autores entendem que existem contradições sem a negação, como: “sou gordo e sou magro”. Em tese essa é uma contradição sem o uso da negação. Mas repare que é possível interpretar que ser magro é a negação de ser gordo (se só existirem essas duas classificações), de modo que “sou magro” na verdade significa “não sou gordo”, ou seja, essa frase seria “sou gordo e não sou gordo”, contendo, ainda que implicitamente, o conectivo de negação.

d) Não existem contradições com apenas uma letra sentencial (considerando que ela pode ser utilizada mais de uma vez).
ERRADO. A frase “p e ~p” é uma contradição com apenas uma letra sentencial.

e) Existem tautologias que só possuem os conectivos de disjunção e conjunção.

ERRADO. Observe que tautologias usando a disjunção e/ou a conjunção, como “p ou ~p” e “(p e p) --> p”, sempre usam também outro conectivo.

Resposta: C
Não existem contradições sem que ocorra o conectivo de negação ????

Dá para fazer a contradição de uma proposição utilizando o conectivo (ou...ou) também.
Exemplo: OU P OU P= FALSO
Disjunção exclusiva só será verdadeira se forem diferentes.
reparem no enunciado ! ele nao menciona disjunção exclusiva.
Eu não entendi a explicação de porque a E está errada. Alguém tem um exemplo com frases?
Lembrem-se de que P v ~ P é sempre TAUTOLOGIA.
Alguém poderia me explicar a D e a E ? pq estão erradas ?
GAB: C

Não existe contradições sem que ocorra o conectivo de negação.

Isso se dá porque, ao analisarmos os conectivos considerados pela questão (ou; e; se... então), não existe situação em que, para que ocorra uma contradição, não haja pelomenos uma preposição negativa.

Para o conectivo "ou" ter valor negativo deve-se ter as duas preposições negativas;
Para o conectivo "e" deve-se ter pelo menos uma das preposições negativas;
Para o conectivo "e... então" deve-se ter o consequente negativo.
https://www.youtube.com/watch?v=ilUE1jPP0V4&t=1903s MIN 24:05
Gabarito: C
Por menos questões assim kkkkkk
que negócio é esse tautologia? chato mesmo!
Aprendi que: "Está claro e está escuro" é uma contradição e não possui conectivo de negação, ou seja, não entendi essa matéria ainda.
solução compacta:

A: errada, por conta de "p --> p"

B: errada, por conta de "~(p e ~p)"

C: correta, propriedade da negação

D: errada, por conta de "p e ~p"

E: errada, mesmo motivo da letra C.

ID

939625

Banca

CESPE / CEBRASPE

Órgão

IBAMA

Ano

2013

Provas

CESPE - 2013 - IBAMA - Analista Ambiental - Tema 2

Disciplina

Raciocínio Lógico

Assuntos

Considere que as proposições sejam representadas por letras maiúsculas e que se utilizem os seguintes símbolos para os conectivos lógicos: ∧ – conjunção; ∨ – disjunção; ⇒ – condicional; ⇔ – bicondicional.
Nesse sentido, julgue os itens seguintes.

A proposição “Se João implica com Maria e Maria implica com João, então evidencia-se que a relação entre João e Maria é conflituosa” pode ser corretamente representada por [P ⇒ Q) ∧ (Q ⇒ P)] ⇒R

Alternativas

Certo

Errado

Comentários

A proposição é: Se João implica com Maria e Maria implica com João, então evidencia-se que a relação entre João e Maria é conflituosa.

Dessa forma:

João implica com Maria = P
Maria implica com João = Q
Relação entre João e Maria é conflituosa = R

A representação correta seria:
(P ∧ Q) ⇒ R
O CONECTIVO CONDICIONAL É:
IMPLICA EM, DIFERENTE DE IMPLICA COM...

ISSO PARA PEGAR O CANDIDATO DESATENTO E SER INDUZIDO A PENSAR QUE AS PROPOSIÇÕES INICIAIS TRATARIAM DE CONDIÇÕES.

MUITO LEGAL A PEGADINHA.
Na verdade, não foi essa a pegadinha Fagner.

A pegadinha da questão é que ela dá a entender que se trata de uma bicondicional (nada tendo a ver com o verbo implicar), pois um pratica uma ação em relação ao outro e vice-versa.
Acontece que essa relação entre os dois é diferente de uma bicondicional.
Seria uma bicondicional se fosse: "João implica com Maria se e somente se Maria implica com João", ou então: "Se Maria implica com João, então João implica com Maria, e se João implica com Maria, então Maria implica com João". E, assim sendo, a questão estaria correta.
P: Se joão implica com maria
Q: Maria implica com João
R: A relação entre Maria e João é conflituoso

Ficaria assim:
(P ∧ Q) ⇒ R
O FAGNER BERNARDINO DE LIMA esta certo, sim!!!
A pegadinha está principalmente em implicar em/com, que são bem diferentes em lógica, mas que na hora da prova pode derrubar muita gente.
Rodrigo e Fagner:

Não pude deixar de manifestar: Infelizmente, vcs estão errados, quanto à regência do verbo implicar.

Implicar é um verbo transitivo direto, quando assume o sentido de acarretar, envolver: A compra de um carro implica gastos desnecessários;

Quando assume o sentido de ter implicância, brigar, discutir, a sua transitividade passa a ser indireta e exige a preposição: O aluno implica com o professor, pois seu sentido é o aluno briga com o professor e não o aluno implica em professor ou o aluno implica professor. Mesmo porque, implicar em é diferente de implicar com.... Eu não posso dizer João implica em Maria, como sugeriu Fagner.

Desculpem-me por tratar de regência em questões de raciocínio lógico.

Mas considero que, nesse caso, até a regênciado verbo Implicar algo ou implicar com, faz parte de um raciocínio lógico, não matemático, mas cultural.
Um comentário extra:
Detestei essa nova ordenação e a renomeação dos assuntos de Raciocínio Lógico, aqui no site. O que era perfeitamente ordenado conforme os nomes dos assuntos cobrados nos editais de concurso, foi mudado pra um único tema: "p. Raciocínio Lógico-Psicotécnico". Os outros assuntos são referentes a matemática e nada se confunde com Raciocínio Lógico.
Já solicitei à equipe QC a revisão dessa "infeliz" mudança de assuntos e a reordenação de acordo como estava antes. Quem concordar, e quiser ajudar, fica o apelo a vcs para enviarem à equipe QC (Através do link "Atendimento") a sugestão de reordenação dos assuntos, conforme estava listada anteriormente aqui no site!
Grato!
GABARITO: ERRADO
Um meio mais fácil de perceber se o verbo implicar é ou não uma condicional, reside na quantidade de verbos e na relação de causa-consequência estabelecida pela condicional.

Note que o verbo implicar (VTI = ter implicância), neste caso, não está relacionado a uma condicional, pois se trata apenas de uma ação isolada que não resulta em outra, como ocorre na condicional. Observe a diferença:

"Chover implica fazer frio" – Neste caso, há uma condicional, pois há uma relação de causa-consequência. O fato de chover (CAUSA) resulta em fazer frio (CONSEQUÊNCIA);
Observe também que nesta sentença há a presença de dois verbos, logo temos duas proposições simples ligadas por um conectivo lógico, resultando em uma proposição composta.
Na sentença "Se João implica com Maria e Maria implica com João, então evidencia-se que a relação entre João e Maria é conflituosa", percebe-se que há apenas um verbo em cada sentença e não há a relação de causa-consequência estabelecida pela condicional, logo temos duas proposições simples ligadas APENAS pelo conectivo "e". Logo, o gabarito correto é:
P ^ Q → R
Conheçam e inscrevam-se no meu canal no youtube, pois sou professor de Matemática e gravei alguns vídeos com dicas e bizus de Matemática e Raciocínio Lógico.
Link do canal: https://www.youtube.com/channel/UC_FQm8aivYBf2q6ga1rxklw
Face: JULIO CESAR SALUSTINO
Realmente não entendi o motivo de não ser um condicional. Como posso perceber a diferença num caso como esse em que Se então representa apenas P contra uma situação de fato condicional?
“Se João implica com Maria e Maria implica com João, então evidencia-se que a relação entre João e Maria é conflituosa
P: João implica com Maria
Q: Maria implica com João
R : relação conflituosa.
P ^ Q ---> R
A Implica COM B é diferente de A implica B.
Proposição P: "João implica com Maria"
Proposição Q: "Maria Implica com João
Proposição R: "A relação de João e Maria é conflituosa
P ^ Q ---> R
MAS CUIDADO! Se a proposição acima fosse equivalente a [P ⇒ Q) ∧ (Q ⇒ P)] ⇒R o gabarito seria Certo. Então ainda é necessário conferir se as proposições são equivalentes para definir a resposta. Recomendo a tabela verdade
De todo modo, as proposições não são equivalentes e portanto o gabarito: E
São equivalentes, por exemplo:
P ^ Q ---> R = ~R ---> ~P v ~Q = (~P v ~Q) v R
É sabido que a proposição “Se João implica com Maria e Maria implica com João, então evidencia-se que a relação entre João e Maria é conflituosa”, contém uma condicional e uma conjunção, logo podemos reescreve-la da seguinte maneira:

(P ^ Q) ⇒R

Onde:

P = João implica com Maria

Q = Maria implica com João

R = evidencia-se que a relação entre João e Maria é conflituosa

O enunciado afirma que a proposição acima pode ser corretamente representada por:

[(P ⇒ Q) ^ (Q ⇒ P)] ⇒R

Nem se aplicarmos a lei de Morgan nesta proposição, chegaremos a proposição correta, (P ^ Q) ⇒R.

RESPOSTA: ERRADO
Eu vejo P e Q então R
(P ^ Q) -> R

GAB. ERRADO
É PARA TER CUIDADO :

João implica com Maria : uma única proposição. ( ideia que João é intimão...kkk..todo mundo já sofreu disso...cuidado com sentido.)

João implica Maria : A-> B.

FORMAS DE SE EXPRESSAR UMA CONDICIONAL: Se A, B.

B, se A.

Todo A é B.

A implica B.

A somente se B.

A é suficiente para B.

B é necessário para A.

FONTE : Apostila Raciocínio Logico.

GABARITO 'ERRADO"
E simples a palavra implica quer dizer implicancia.
Esse 'IMPLICA' da frase é apenas um verbo e não o 'implica' como sinônimo de 'condicional'. Temos que ficar ligados nessas pegadinhas..
Comentário fraco do professor... o que adianta ser mestre e estudante de pHD se não consegue transmitir, elucidar a pegadinha da banca? A maldade com a língua portuguesa? Eu caí que nem um bobo na questão. Afoito, um pouco nervoso de uma questão anterior que errei não consegui compreender quando fiz na primeira vez. Resolvi ela automaticamente substituindo cada implicar por uma condicional e fui induzido pela maldade da banca! Implicar aqui é sinônimo de irritar, qualquer coisa do tipo. Agora mais calmo vejo isso com clareza. Pra ver como estar num ´bom dia´ para resolver uma prova tem influência.
Excelente comentário do Professor, que explicou super bem e claro, além de conseguir transmitir o raciocínio. Quem não entendeu precisa ver mais vídeo aulas.
Está muito fácil ver que a proposição pode ser representada por (A ^ B) -> C

Eu tive a impressão que a banca tentou convencer que é possível usar a propriedade distributiva na condicional, o que não é possível. Tanto é que se você simular uma propriedade distributiva, dará algo parecido com o que diz o enunciado. Utilizando essas letras que eu propus, vejam:

(C --> A) ^ (C --> B)

Não sei se a banca induziu a pensar dessa maneira. Só um palpite. Todos nós sabemos que não é possível distributiva em condicinal.
boa tentativa, cespe
Vamos separar os conectivos para identificarmos as preposições simples: “Se João implica com Maria e Maria implica com João, então evidencia-se que a relação entre João e Maria é conflituosa”
Já podemos concluir que esta frase possui dois conectivos: Condicional (Se... então) e a conjunção (e).
Podemos resumir da seguinte forma:
Proposição P: "João implica com Maria" Proposição Q: "Maria Implica com João Proposição R: "A relação de João e Maria é conflituosa Ficando da seguinte forma: P ^Q R
Portanto, nosso gabarito está errado.
(P ^ Q) -> R
GAB: ERRADA

É nítida na representação o erro. [P ⇒ Q) ∧ (Q ⇒ P)] ⇒R

o CERTO é: [P^Q] ->( R)

ID

939628

Banca

CESPE / CEBRASPE

Órgão

IBAMA

Ano

2013

Provas

CESPE - 2013 - IBAMA - Analista Ambiental - Tema 2

Disciplina

Raciocínio Lógico

Assuntos

Considere que as proposições sejam representadas por letras maiúsculas e que se utilizem os seguintes símbolos para os conectivos lógicos: ∧ – conjunção; ∨ – disjunção; ⇒ – condicional; ⇔ – bicondicional.

Nesse sentido, julgue os itens seguintes.

A proposição “Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia” pode ser corretamente representada por P∧Q.

Alternativas

Certo

Errado

Comentários

Correto.
Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia.
P ^ Q
somente complementando o ótimo comentário acima, o CESPE vem mudando sua maneira de elaborar questões e o que poderia confundir o candidato nessa questão seria aquela vírgula após a palavra "expressão". Mas com eficiência nosso colega deixou clara a resolução da questão.

Realmente é P^Q.

Força galera!
A banca tenta confundir colocando proposições gigantescas, é bom ficar atento para não se perder. Apesar de expressões enormes não passa de uma proposição simples ;)
QUESTÃO CORRETA
Para melhor visualização, destaco primeiramente os verbos e conectivos, vejamos: A proposição
“Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia” pode ser corretamente representada por P∧Q.
Observem que temos duas proposições simples que ligadas a um conectivo, representam uma proposição composta.
Onde:
P: Fiscalizar os poderes constituídos é um dos pilares da democracia (proposição simples, representada por um único verbo "É" = "SER", quanto ao verbo "FISCALIZAR", apenas, se apresenta como uma das formas nominais do verbo, ou seja, "infinitivo")
e (conectivo = conjunção, representada pelo símbolo ∧)
Q: garantir a liberdade de expressão, outro pilar da democracia (proposição simples, representada por um único verbo "É" = "SER", o qual está elíptico na oração, por meio da "," - agora, quanto ao verbo "GARANTIR" segue o mesmo raciocínio do verbo "FISCALIZAR", são apenas formas nominais do verbo).
Portanto, a proposição acima poderia ser corretamente representada por P∧Q.
Caso alguém entenda diferente e puder contribuir, agradeço.
Apenas complementando a resposta do colega acima, esta é a famosa vírgula vicária, que promove a supressão de um termo, neste caso o verbo E´.

ABS
Pessoal!!!

Cada proposição possui obrigatoriamente um verbo???

Espero que possam responder minha pergunta.
Obrigada desde já ;)
Bons estudos!
Não necessáriamente, Rafaela, pois: "2 + 3 = 7" é uma preposição simples e falsa.
bem como, " se natalense, brasileiro", (A --> B) também é uma proposição sem verbo.
Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia......... se ambos sao considerados pilares da democracia não poderia ser representado por P v Q, ou seja, tanto um quanto o outro sao considerados pilares? Mesmo que tal possibilidade fosse aceita....este fato não mudaria a resposta da questão, já que a forma P ^ Q também PODERIA representar a proposição dada!

O que voces acham?
Dá pra pensar que é até uma pegadinha! rsrs
SIMPLES E RÁPIDO: PERCEBA QUE A VÍRGULA ANTES DA PARTE "outro pilar" vem no lugar do verbo "é", portanto temos dois verbos, dois sujeitos, duas orações com sentido, uma conjunção E implícita, logo a representação está correta.
a vírgula está relacionada com a economia linguística - coesão do texto.
Resolvi assim:

“Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia”
1 - Fiscalizar os poderes constituídos é um pilar da democracia (P)
2 - garantir a liberdade de expressão é um pilar da democracia (Q)
Fiscalizar os poderes constituídos é um pilar da democracia E garantir a liberdade de expressão é um pilar da democracia
P^Q
Reescrevendo a proposição:

“Fiscalizar os poderes constituídos é um dos pilares da democracia e outro pilar da democracia, é o de garantir a liberdade de expressão.”

Assim:

P = Fiscalizar os poderes constituídos é um dos pilares da democracia

Q = outro pilar da democracia, é o de garantir a liberdade de expressão.

Ou seja: P ^ Q

Resposta: Certo.
É necessário ficar atento, pois essa assertiva é basicamente simples mas se tratando de CESPE sempre achamos que existe uma pegadinha.

GAB CERTO
Essa questão tenta pegar quem já está mais "avançado".
A proposição “Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia” pode ser corretamente representada por P∧Q.

Certo. Duas ideias ligadas ao conectivo ''e''.
@Luciana Serrano, a proposição desta questão é composta.
Sinceramente essa cespe é um absurdo, concordo e assino embaixo que isso é uma proposição composta, mas de tanto fazer esse tipo de questão com o verbo implícito com o gabarito dizendo que era uma proposição simples ( DA PRÓPIA CESPE ) , já não sei mais o que faço --'.
, = é
Gabarito: CORRETO

Novamente devemos reescrever a frase identificando os conectivos e as preposições simples:
• “Fiscalizar os poderes constituídos é um dos pilares da democracia e garantir a liberdade de expressão, outro pilar da democracia”.
Podemos verificar que esta frase possui apenas um conectivo: A conjunção (e).

Podemos representar as preposições simples da seguinte forma:
P = Fiscalizar os poderes constituídos é um dos pilares da democracia
Q = garantir a liberdade de expressão, outro pilar da democracia

Desta forma, esta frase pode ser representada da seguinte forma: P ^ Q, portanto, gabarito correto.

Fonte: ESTRATÉGIA CONCURSOS
✅Gabarito Certo.
"Fiscalizar os poderes constituídos é um dos pilares da democracia e( ^ ) garantir a liberdade de expressão, outro pilar da democracia”
- P ^ Q é a representação da proposição composta
Bons estudos!✌
que ridículo
foi o equivalente a dizer "X é pilar da democracia e Y é pilar da democracia"
FISCALIZAR os poderes [...] e GARANTIR a liberdade [...]
P ^ Q

Correto

ID

955138

Banca

CESPE / CEBRASPE

Órgão

MPU

Ano

2013

Provas

CESPE - 2013 - MPU - Técnico Administrativo

Disciplina

Raciocínio Lógico

Assuntos

Nos termos da Lei n.º 8.666/1993, “É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração”. Considerando apenas os aspectos desse mandamento atinentes à lógica e que ele seja cumprido se, e somente se, a proposição nele contida, — proposição P — for verdadeira, julgue o item seguinte.

O gestor que dispensar a realização de nova licitação pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a referida lei.

Alternativas

Certo

Errado

Comentários

Eminentes colegas,

Alguém saberia dizer por que essa questão foi considerada errada?

Saudações a todos.
Simples,
Sendo P1 "quando não aparecerem interessados em licitação anterior"
Sendo P2 "esta não puder ser repetida sem prejuízo para a administração"

Conforme o enunciado, "Considerando apenas os aspectos desse mandamento atinentes à lógica e que ele seja cumprido se, e somente se (<-->)"

Dessa forma, é necessário que ambas as premissas sejam verdadeiras ou falsas, para que a proposição seja verdadeira.

Tabela verdade:

V V V
V F F
F V F
F F V
Obrigado, senhor Raphael. Já ajudou a clarear um pouco mais.

Então, não dá para saber se o gestor descumpriu ou não a lei, sem considerar a premissa P2 (se a licitação poderá ser repetida sem prejuízo para a Administração). Nesse caso, para tornar a assertiva correta, uma adaptação seria trocar "descumprirá" por "poderá descumprir".

Saudações.
Primeiramente devemos atentar para o fato de que devemos considerar apenas os aspectos lógicos, ou seja, nada de tentar resolver a questão pela lógica da lei. Então vamos achar as proposições e transformá-las em letras para não sermos contaminados pelo que está escrito:

~A: não aparecerem interessados em licitação anterior
~P: esta não puder ser repetida sem prejuízo para a administração
D: dispensável a realização de nova licitação

Lembro que "quando" equivale a "se". Montando a proposição composta temos:

~A e ~P --> D

Diante da proposição, quando a questão afirma que "o gestor dispensa a realização de nova licitação" o D é verdadeiro, sendo o D verdadeiro a proposição ~A e ~P --> D só pode ser verdadeira, logo a lei não é descumprida e sim cumprida.

GABARITO: ERRADO
As proposições lógicas são afirmações de sentido completo, em que é atribuída uma característica a um sujeito, sendo avaliada apenas em verdadeiro ou falso.

Análise do texto 1:
Na frase dada, temos 3 proposições.

“É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração”.
proposição A: é dispensável a realização de nova licitação;
proposição B: não aparecerem interessados em licitação anterior;
proposição C: esta (licitação anterior) não puder ser repetida sem prejuízo para a administração.
Veja, que todas as proposições seguem a definição, inclusive a proposição C, que é a mais longa. Repare que a proposição C não pode ser dividida em outras proposições, pois não faria sentido dizer:
C1: esta (licitação anterior) não puder ser repetida
C2: esta (licitação anterior) sem prejuízo para a administração.

Os conectivos da frase são "quando" e "e". Então, da frase tiramos a proposição P de que fala o texto 2:
P = (B^C) -> A
O termo antecedente (à esquerda da seta) é parte do grupo maior, o consequente (indicado a direita da seta). Por isso, mesmo que o texto esteja escrito na ordem inversa (fala-se antes de A para depois falar-se em B e C), a proposição P só pode ser escrita dessa forma.

Análise do texto 2:
"Considerando apenas os aspectos desse mandamento atinentes à lógica e que ele seja cumprido se, e somente se, a proposição nele contida, — proposição P — for verdadeira"

A primeira informação é sobre a restrição para resolver os itens. Não podemos usar conhecimentos da Lei 8666/93. Apenas podemos avaliar as proposições pela lógica.
A segunda informação é que a lei só será cumprida (proposição L) se e somente se a proposição P for verdadeira. Ou seja, o texto informa que L e P são equivalentes, terão o mesmo valor. Isso só acontece na primeira e última linhas da tabela verdade de Q = L <--> P
L  P  Q
V  V  V
V  F  F
F  V  F
F  F  V
Considerando tudo isso exposto no comentário acima, segue a resposta do item:

O gestor que dispensar a realização de nova licitação pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a referida lei.

A forma mais demorada para demostrar isso é pela tabala verdade contendo todas as possíveis combinações de B, C, A, (B^C) e P.

Porém existe uma forma mais rápida de chegar a resposta, conhecer a tabela verdade da "implicação" (->).
No texto 2 temos a informação de que a licitação esta dispensada. Ou seja, o valor de P é verdade.

P = (B^C) -> A
Como A é verdadeiro (licitação dispensada), o valor de P também é verdadeiro, independentemente do valor de (B^C).
Se P é verdadeiro e L tem valor igual a P, logo temos que L é verdadeiro!
L verdadeiro siginifica cumprir a Lei. O item afirma que a Lei foi descumprida e por isso é um item ERRADO.
A: é dispensável a licitação
B: não apareceram interessados na licitação anterior
C: a licitação não pode ser repetida sem prejuízo à administração

P: (B^C)->A

Tendo em mente a tabela verdade do condicional "se", sabe-se que sempre que a consequência for verdadeira a proposição será verdadeira também. Assim, ainda que cause prejuízo a administração e tenham aparecido interessados na licitação anterior, logicamente, a proposição "p" está correta, já que A é verdadeira - a licitação foi dispensada. Assertiva correta.
Considerei a questão Errada, por ela mensionar ''...pelo simples fato...'', enquanto que ela precisava das duas premissas p estar certa.
```
Aqui vai outra explicação partindo do básico pra quem ainda tá com dúvida
```
1º Passo: identificar os elementos da questão

a) Quem é essa tal de proposição P?
- A proposição P é o que está contido na Lei, ou seja, P = "É dispensável ... quando ... administração".
- A palavra "quando" já dá a ideia de que estamos diante de uma proposição condicional, já que "Se A, então B" é o mesmo que "Quando A, então B".
- Voltando à proposição P: Quando acontecer o quê, então vai acontecer o quê? Ora, quando "não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo pra adm", então "será dispensável a realização de nova licitação".
- Percebemos que tem um conectivo "e" ali no meio da condição, então vamos dividir as orações em duas estruturas: Vamos representar "não Aparecerem interessados em licitação anterior" por ~A e "esta não puder ser Repetida sem prejuízo para a administração" por ~R. O resultado, por sua vez, vamos representar por "D" (dispensável).
- Logo: Se ~A e ~R, então D. Ou seja: ~A ^ ~R --> D

b) A questão fala que só há cumprimento da lei se e somente se P for verdadeiro.
- Vamos representar Cumprimento da lei por C.
- Já sabemos que "se e somente se" é uma bicondicional e que, pra ser verdadeira, as duas sentenças só podem ser ambas verdadeiras ou ambas falsas.
- Traduzindo, fica: C <--> P.

2º passo: comparar as proposições com o item da questão

a) O que diz o item?
- "O gestor que dispensar a realização de nova licitação pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a lei."

Vamos destrinchar a sentença:
1. Não apareceram interessados em licitação anterior (ou seja, ~A).
2. O gestor dispensa a realização de nova licitação (ou seja, D).
3. O gestor, fazendo isso, está descumprindo a lei (se cumprir a lei é C, então descumprir é ~C).

Já temos as seguintes proposições:
C <--> P
P: ~A ^ ~R --> D

b) Mãos a obra!
- Pra sabermos se ele Cumpriu (C) ou Descumpriu (~C) a lei, temos que verificar se P é verdadeiro (V) ou falso (F) na hipótese trazida pelo item.
- Sabemos que a licitação foi dispensada, logo, D é verdadeiro.
Ou seja, P: ~A ^ ~R --> V
- Sabemos que uma conjunção (estrutura com o conectivo ^) só será verdadeira se ambas as sentenças forem verdadeiras (acontecerem). Ora, o item diz que só aconteceu uma das sentenças (~A), logo essa conjunção é falsa! Ou seja, P: F --> V
- Sabemos também que só há uma forma de um condicional ser falsa: Se a condição for V e o resultado for F. Não é o caso dessa hipótese! Se a condição for F e o resultado for V, a condicional é verdadeira! Logo, P = V
- Se P = V, então C é verdadeiro, ou seja, a lei é cumprida!
- O item diz que a lei é DESCUMPRIDA (~C), portanto o item é falso.
Na vida real, quando você for servidor público, nunca dispense uma licitação sem ter certeza que atende todas as condições que a lei determina, princípio da legalidade estrita, o agente público no exercício da função pública só pode fazer o que a lei determina, o raciocínio desta questão só serve para o dia da prova e nas questões de raciocínio lógico OK, no meu entender não se deve colocar em uma prova uma questão como esta, seria mais adequado não usar os artigos da lei neste tipo de questão.
Ótima resolução do Prof. Vitor Menezes:

http://exatasparaconcursos.wordpress.com/2013/06/04/rlq-mpu-2013-parte-1/
A: é dispensável a realização de nova licitação;
B: não aparecerem interessados em licitação anterior;
C: esta não puder ser repetida sem prejuízo para a administração.

UMA DÚVIDA: Pq a proposição extraída do enunciado da lei não poderia ser assim:

A <--> (B^C)

???
não sou novo nisso...mas achei o enunciado realmente confuso...
e mt estranho quando verificamos que se a licitação for dispensada, independente do motivo, não ha descumprimento da lei, mt pelo contrario, aih ocorre de pronto o entendimento que a lei foi cumprida..
A questao expoe que se a preposiçao P for verdadeira há necessariamente o cumprimento da lei e depois de refletir um pouco sobre o assunto não sei se consigo concordar....
bem só expus minha reflexão aqui.
bom estudo a todos.
Podemos entender de 2 formas:
D= É DISPENSÁVEL a realização de nova licitação
I= quando não aparecerem INTERESSADOS em licitação anterior E
R= esta não puder ser REPETIDA sem prejuízo para a administração”.
a proposição ficaria:
(¬ I ^ ¬R) => D
A questão diz que a proposição será sempre verdadeira D=V; e I ou R= V ou F
Tanto o I como o R sendo falso ou verdade a proposição dará verdade então ele cumprirá a lei e a questão diz que ele DEScumprirá. este é o erro da questão.
O gestor que DISPENSAR a realização de nova licitação pelo simples fato de não ter aparecido INTERESSADOS em licitação anterior DESCUMPRIRÁ a referida lei.
Quebrando a proposição P “É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração”, temos:

D: é dispensável a realização de nova licitação

I: aparecerem interessados em licitação anterior

R: esta não puder ser repetida sem prejuízo para a administração

É sabido que a palavra “quando” remete ao condicional, reescrevendo a proposição P de uma forma conveniente:

“Se não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração, então é dispensável a realização de nova licitação.”

P: (~ I ^ ~R) → D

O enunciado nos diz que o gestor dispensa a realização de nova licitação, logo D é verdade.Quando temos o consequente da condicional verdadeiro, não importa o antecessor, toda a condicional será verdadeira.

Assim ele cumprirá a referida lei independentemente do valor lógico de (~ I ^ ~R).

RESPOSTA: ERRADO
Errado
- NO BICONDICIONAL PARA SER VERDADEIRO AS DUAS PROPOSIÇÕES SÃO VERDADEIRAS OU SÃO FALSAS
- LOGO: se é dispensável a realização de nova licitação quando não aparecem interessados em licitação anterior (V) se , e somente se, está não puder ser repetida sem prejuízo para administração (V) . V <---> V = V
- se é dispensável a realização de nova licitação quando não aparecem interessados em licitação anterior (F) se , e somente se, está não puder ser repetida sem prejuízo para administração .(F). F<---> F = V

~ILA ^ ~PSR -> DNL
Pessoal, quanto à resolução da questão, tudo bem! Mas como posso considerar que a DISPENSA eh verdadeira se quem me diz isso não é o enunciado, e sim a assertiva que vou julgar ser V ou F?

Isso que ainda não consegui entender. Alguém poderia me ajudar?
Deus do céu, não precisa de 3 kilos de texto pra justificar a questão, é mais simples:
A: É dispensável a realização de nova licitação
B: Aparecerem interessados em licitação anterior
C: Esta pode ser repetida sem prejuízo para a administração
P: A <-> (~B^~C) = Verdadeiro
Ora, na assertiva ele diz que A e B são verdadeiros, mas nada sobre C, então:
V <-> (V ^ ~C) = Verdadeiro.
Caso C seja verdadeiro, o servidor não descumpriu a lei. Já que não há como afirmar algo com certeza (há ambiguidade em uma das proposições, C) a questão como um todo está errada.
O funcionário público só pode fazer o que a lei determina. Se a lei determina, não estará descumprindo a lei. No caso em pauta é interpretação lógica.
Nos termos da Lei n.º 8.666/1993, “É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração”.

Considerando apenas os aspectos desse mandamento atinentes à lógica e que ele seja cumprido se, e somente se, a proposição nele contida, — proposição P — for verdadeira, julgue os itens seguintes.

O gestor que dispensar a realização de nova licitação pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a referida lei.

Quebrando a proposição P “É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração”, temos:

D: é dispensável a realização de nova licitação

I: aparecerem interessados em licitação anterior

R: puder ser repetida sem prejuízo para a administração

É sabido que a palavra “quando” remete ao condicional, reescrevendo a proposição P de uma forma conveniente:

“Se NÃO aparecerem interessados em licitação anterior e esta NÃO puder ser repetida sem prejuízo para a administração, então é dispensável a realização de nova licitação.” NEGAÇÕES

P: (~ I ^ ~R) ---> D

TABELA VERDADE DA CONDICIONAL
a b a-->b
V V V
V F F
F V V
F F V

SE O ANTECEDENTE É VERDADEIRO ENTÃO A PROPOSIÇÃO É TODA VERDADEIRA, POIS ELE DIZ QUE A PROPOSIÇÃO 'P' É VERDADEIRA.
ASSIM ELE CUMPRIRÁ A REFERIDA LEI.
O QUE O ENUNCIADO DIZ É QUE ELE NÃO CUMPRIRÁ, O QUE NÃO É VERDADE.
GABARITO ERRADO.

Assistir o vídeo do professor Vitor Menezes https://exatasparaconcursos.wordpress.com/2013/06/04/rlq-mpu-2013-parte-1/
Questão bastante complexa!
Este video explica!!
https://www.youtube.com/watch?v=W2aRiytoht4
Bons estudos.
Acertei esta questão sem usar tabelas-verdade ou armando a proposição P em condicional ou bicondicional.
No final do enunciado afirma que o gestor "...descumprirá a referida lei".
Como o procedimento está nos termos da lei 8.666/1993, ele não descumprirá a lei.
Questão errada. Bons estudos, colegas.
quilos e quilos de textos por uma resolução bem simples. k
Gab: ERRADO
Pessoal,

Não poderíamos apenas pensar da seguinte maneira:

A lei diz que é DISPENSÁVEL a licitação CASO não apareçam interessados.

DISPENSÁVEL = não necessária

INDISPENSÁVEL=necessária / importante

Portanto se o gestor dispensou pelo fato de não ter havido interessados ele NÃO descumpriu a lei.

Creio ser simples, se eu estiver errado por favor me corrijam.

Abraços...
AI QC LEI 8666 EM RACIOCÍNIO LÓGICO AH ESSAS HORAS ACHO Q É UM SINAL P/ PARAR POR HJ KKKKKKKKKKKKKKKKKKKK
adriano isso é raciocinio, e nao direito adm.
ERRADO

Tínhamos 2 condições para a dispensa da licitação :

( I ) - É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior

( II ) - esta não puder ser repetida sem prejuízo para a administração

Como no enunciado ele disse que era "se somente se " = Bi Condicional

Haveria a necessidade das duas condições para o descumprimento da lei

e ele só fala na (I) condição .

O gestor que dispensar a realização de nova licitação pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a referida lei.
Resolvi essa questão da forma como foi dada no enunciado, ou seja, A > (B ^ C).
Procurei em outros fórum e vi várias resoluções dessa questão partindo da mesma premissa que a da maioria dos comentários, ou seja, (B ^ C) > A.
Só que parece tão claro que a condicional vem antes da conjunção que não vejo porque de resolvê-la da segunda forma.
Alguém poderia "encontrar" o erro de da premissa de eu está partindo de A > (B ^ C), e não de (B ^ C) > A?
Di Alley, a palavra Quando indica o início da condicional, por isso a parte "É dispensável a realização de nova licitação" é o consequente.
É muito estranho ver pessoas acertando com um fundamento totalmente equivocado. Não se trata de bicondicional, é apenas condicional mesmo. A explicação do professor está bem sintética, mas é a correta.

Pela lógica, mesmo se não ocorrer nenhuma das condições anteriores, o gestor pode dispensar a licitação. Nessas horas, você deve esquecer o princípio da legalidade estrita. Em condicional, só dá falso se o consequente for falso e o antecedente verdadeiro.
Eu acertei o gabarirto (ERRADO) fazendo da seguinte maneira:

p: "...quando não aparecerem interessados na licitação anterior"

q: " ... esta não puder ser repetida sem prejuízo para a administração"

n: " É dispensável a realização de nova licitação..."

Temos três proposições simples formando uma composta, e dois conectivos para analisarmos (a conjunção primeiro, e a condicional depois). Pela tabela da conjunção, só é V se ambas (p e q) forem V; e, pelo contexto, apenas p é V ( "...pelo simples fato de não ter aparecido interessado em licitação anterior"), sendo q F. Dessa forma, já temos o primeiro resultado (p ^ q é F). Depois, pegamos esse resultado e analisaremos com a proposição n, que é V (pois o administrador já dispensou a licitação). Pela tabela da condicional, só V-->F dá F, sendo V em todo o resto, o que nos dá o resultado F --> V = V para a proposição composta.

Pela fórmula: "Se p e q, então n" - p ^ q --> n

F --> V == V (Pela lógica sentencial a proposição é VERDADEIRA, então o administrador cumpriu a lei.)
questão bonita, mas não hora eu errei rsrs

proposição P = cumprir a lei
p = ~I ^ ~R --> D
- o gestor já dispensou a licitação, logo D é Verdadeiro
- antes da dispensa, é sabido que não acudirem interessados, logo ~I é verdadeiro

só com essas duas informações, eu sei que a proposição ~I^ ~R --> D toda é verdadeira, pois mesmo sem saber o ~R, o resultado de ~I^ ~R seja ele V ou F gerará uma tabela verdade de condicional verdadeira:
V -->V =V
F -->V = V

se, independente do prejuizo ~R, a condicional só pode ser verdadeira, P é verdadeiro e P significa o cumprimento da lei

resposta: não há descumprimento da lei se realizar a dispensa de licitação apenas por não acudirem interessados em licitação anterior
Os comentários dos professores de Ráciocinio Lógico deveriam ser todos por VÍDEOS.
Errado

Entendi da seguinte forma:

“É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração”.

Como trata se de uma BiCondicional (<-->) "... e que ele seja cumprido se, e somente se, a proposição nele contida..."

É necessário que ambas as informações sejam ou verdadeiras ou falsas para que a proposição composta seja verdadeira.

Tabela verdade:
(<-->)
V V V
V F F
F V F
F F V

"O gestor que dispensar a realização de nova licitação pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a referida lei."

Não descumprirá porque para que seja verdadeira (descumprir a lei) ambas as informações devem ser F ou V como mostra a tabela verdade. Como a questão informa apenas a primeira informação, então não é suficiente para julgar se o gestor descumpriu a lei.

Sou novo nesse tipo de questão. Qualquer bobagem minha é só dar um toque.

Bons estudos.

Take it easy...
É dispensável a realização de nova licitação quando não aparecerem interessados em licitação anterior e esta não puder ser repetida sem prejuízo para a administração.

F F= >V

Meus amigos, fiquei um com um pouco de duvida a respeito da questão. comente a respeito para que eu possa ter um melhor intendimento.
Gabarito errado

Entendi que a questão manda Considerar apenas os aspectos à lógico. Sendo assim deconsiderei a lei e considerei apenas que a preposição P é verdadeira. Sabendo que uma BICONDICIONAL para ser verdadeira precisa de VV ou FF e que P = V, basta analisarmos a preprosição Q(...não ter aparecido interessado em licitação anterior...) para saber se o gestor irá ou não infringir a lei.
No caso da questão, a preposição Q é verdadeira de acordo com o enunciado. Logo VV=V, então o gestor não estará infringindo a lei.
Marquei C, pq achei que era INEXIGIVEL. e não dispensável. Pq na inexigibilidade é quando a licitação for deserta? Alguém me explique..
Licitação Deserta
A Licitação Deserta é aquela que nenhum proponente interessado comparece ou por ausência de interessados na licitação. Neste caso, torna-se dispensável a licitação quando a Administração pode contratar diretamente, desde que demonstre motivadamente existir prejuízo na realização de uma nova licitação e desde que sejam mantidas todas as condições preestabelecidas em edital.

https://www.licitacao.net/licitacao_deserta_e_fracassada.asp
a questão é de rlm e nego colocando explicação de lei kkkk
Marquei C pq entendi que pelo simples fato de não aparecer interessados, não daria o direito de não repetir o procedimento. Para não caracterizar descumprimento o gestor teria que repetir a licitação, salvo comprovado que o ato de repetir o procedimento fosse causar prejuízo a administração.
Marquei C pq entendi que pelo simples fato de não aparecer interessados, não daria o direito de não repetir o procedimento. Para não caracterizar descumprimento o gestor teria que repetir a licitação, salvo comprovado que o ato de repetir o procedimento fosse causar prejuízo a administração.
Marquei C pq entendi que pelo simples fato de não aparecer interessados, não daria o direito de não repetir o procedimento. Para não caracterizar descumprimento o gestor teria que repetir a licitação, salvo comprovado que o ato de repetir o procedimento fosse causar prejuízo a administração.
GENTE... ou os comentários estão na questão ERRADA ou está aparecendo para mim errado!
A questão é de LICITAÇÃO e só vejo comentários de RACIOCÍNIO LÓGICO. WTTTTTFFFF!? O.o

Se fosse só 1, de boa, mas 43, é demais.
SE É dispensável... discricionariedade !!!
É RLM agora ?
Nos termos da Lei 8.666/93.... Vc vem observar os comentarios achando q vai encontrar respostas sobre o assunto de licitações e se depara com RLM kkkkkkk
A QUESTÃO É DE RACIOCÍNIO LÓGICO.

O ENUNCIADO DESTA QUESTÃO ESTÁ INCOMPLETO...

A QUESTÃO DIZ: "... considerando apenas os aspectos desse mandamento atinentes à LÓGICA E QUE ELE SEJA CUMPRIDO se, e somente se, a proposição nele contida, - proposição P - for verdadeira, julgue os itens seguintes."
Pelo que entendi a questão está falando de LICITAÇÃO DESERTA, que é quando não aparece ninguém interessado na licitação. Então para dispensar, a administração tem que analisar se realizando uma nova licitação causa prejuízo, se causar ai sim ela pode contratar diretamente e dispensar a licitação.

CERTA - Porque ele descumprirá a referida lei.
a questao é de raciocinio logico !!!!
Neste primeiro item da resolução, vamos aproveitar para fazer uma análise mais detalhada da frase do enunciado. Veja que ela pode ser reescrita assim:

“Se não aparecerem interessados em licitação anterior E esta não puder ser repetida sem prejuízo para a administração, ENTÃO é dispensável a realização de nova licitação”.

Repare que esta frase apresenta um caso onde a licitação é dispensável, mas ela NÃO IMPEDE que a licitação seja dispensável em outros casos TAMBÉM. Resumindo, temos:

P: (não aparecerem interessados E não puder repetir) --> dispensável

Portanto, a frase do enunciado apresenta um caso onde a licitação é dispensável (quando ocorrerem duas condições: não aparecer interessado e não puder ser repetido), mas NÃO IMPEDE que a licitação também seja dispensável quando ocorrer apenas uma dessas condições. Item ERRADO, pois não podemos afirmar que a lei foi descumprida.

Em outras palavras, a lei é descumprida apenas quando a proposição P for falsa. Como P é uma condicional, precisamos que a primeira parte dela seja Verdadeira e a segunda seja Falsa, isto é, precisamos ter V-->F. Isto só ocorre quando:

“não aparecem interessados” é V;
“não puder repetir” é V; e
“dispensável” é F (ou seja, a licitação é indispensável).

Como não foi dito que a licitação era indispensável, nada podemos afirmar sobre o gestor.

Resposta: E
Questão fácil, porém, está faltando um pedaço de texto muito importante para a sua resolução, qual seja: "considerando apenas os mandamentos atinentes à lógica, e que ele seja cumprido, se, e somente se, a proposição nela contida - proposição P - for verdadeira, julgues os itens seguintes:

Perceba, sem esse texto seria impossível considerar ou não que a lei foi cumprida, pois esse texto nos informa que a lei será cumprida quando a proposição for verdadeira.

Veja a questão completa no seguinte vídeo postado pelo colega Alexandre Ferreira:

https://www.youtube.com/watch?v=W2aRiytoht4
DEU BOM MISTURAR RLM COM A LEI DO CAPETA
GAB;ERRADO
Errado, pois tomando A, B e C como:

A (não aparecerem interessados em licitação anterior)
B (esta não puder ser repetida sem prejuízo para a administração)
C (É dispensável a realização de nova licitação)

A sentença será escrita na seguinte ordem = A ^ B ---> C (Pois o "Quando" traz o Se-Então)

A^B é condição suficiente e C condição necessária.

Dessa forma temos que ter A^B para resultar em C -

Ou seja: pela proposição, se acontecer só A (não aparecerem interessados em licitação anterior) não necessariamente resultará em C.

Bons estudos!
LICITAÇÃO DESERTA -> LICITAR / DISPENSAR -> Discricionariedade do ADM
Mistura com estatística inferencial e vai criar uma bomba atômica de estudos kkkkkk
A questão É de raciocínio lógico.
Se não fosse de raciocínio lógico estaria correta!
Não perca tempo!
Vá direto ao comentário do ALEX NASCIMENTO
Bicondicional! Olhem o caput da questão!!!!
porque pegar um texto que pela coerencia gramatical tem uma resposta lógica e pedir pra aplicar uma lógica que contradiz a coerência. a única coisa que esta questão mede é a capacidade do concorrente de abstrair da realizadade.
https://www.youtube.com/watch?v=DeQt-O4UKTY&ab_channel=NEAFConcursos
ERRADO

Teoria: Na condicional para ser verdade, o antecessor poderá ser verdadeiro ou falso, desde que o sucessor seja verdadeiro, sempre será verdadeiro. (V/F -> V = V)

A questão diz:
"É dispensável a realização de nova licitação (A - V/F) quando (->) não aparecerem interessados em licitação anterior (B - V) e esta não puder ser repetida sem prejuízo para a administração”.

E só pega a parte marcada e diz que (pelo simples fato de não ter aparecido interessado em licitação anterior descumprirá a referida lei - (B - V) ),o argumento é FALSO (estará descumprido a lei) então vamos simbolizar e ver se é isso mesmo:

É dispensável a realização de nova licitação (A - V/F) quando não aparecerem interessados em licitação anterior (B - V) = FALSA? (Lembra da teoria?)

A (V/F) -> B (V) = VERDADEIRO

Continue estudando. Você vai conseguir!
Algo lógico não precisa ser coerente, e às vezes nos guiamos pela coerência.
Errei mais uma por esse fato.
P1: A -> (B^C)
P2: A -> B
-------------------
C: A ^ (¬B v ¬C)

Aplicando o método da conclusão falsa, perceberemos ser falsa a assertiva.

Detalhes:
1º "Quando" = "se, então"
2º "pelo simples fato" equivale à "pois" que equivale à "se, então"
3º "descumprirá a referida lei" equivale à negação da proposição inicial e a conclusão proposta pela a assertiva.
Deve ser a argumentação dada pelos governantes aos tribunais de contas kkkk
A primeira coisa a se fazer é colocar a proposição na forma correta. Observe que a presença do " QUANDO " implica em uma condicional disfarçada. A forma correta é:

Se não aparecerem... e esta não puder... ENTÃO é dispensável nova licitação.

A partir daqui começa a brincadeira. Vamos então para a pergunta, que diz que NÃO APARECEU INTERESSADO e se isso implica em DESCUMPRIMENTO DA REFERIDA LEI.
Substituindo a informação dada em nossa proposição, na forma correta, temos:
V /\ (?) --> V
Observe que independente do valor de (?) a condicional será sempre VERDADEIRA, ou seja, é DISPENSÁVEL a nova licitação. A questão diz que ele descumprirá a lei, ERRADO, pois é dispensável.

ID

965137

Banca

CESPE / CEBRASPE

Órgão

ANS

Ano

2013

Provas

CESPE - 2013 - ANS - Analista Administrativo

Disciplina

Raciocínio Lógico

Assuntos

Com relação às proposições lógicas, julgue os próximos itens.

A proposição “A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino” estaria corretamente representada por P -> Q, em que P e Q fossem proposições lógicas convenientemente escolhidas.

Alternativas

Certo

Errado

Comentários

Questão Certa

Seria o mesmo que: "Se a escola não prepara com eficácia o jovem para a vida, então o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino", pois traz uma relação de condicional. O problema é que há um erro no enunciado apresentado pelo Questão de Concursos (P ? Q) que deveria ser uma seta apontada para o "Q" (P → Q), mas na prova consta certinho a setinha, ou seja, muita gente irá errar por conta desse ponto de interrogação!
Obrigado Gisele!

Estava eu quebrando a cabeça para tentar entender a questão rs
Vlw Gisele vc é a melhor alguém tá querendo zoar com a gente :)
Só pra constar:

P é : O ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino.
Q é: A escola não prepara com eficácia o jovem para a vida.

P --> Q

Note que a questão deixa claro que as proposições devem ser convenientemente escolhidas.

O "pois" que determina essa ordem, do contrário não teria sentido.

Se o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino, então a escola não prepara com eficácia o jovem para a vida.
Separando e reescrevendo convenientemente a frase:
“A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino”
Vemos que a proposição acima contem uma relação de causa e efeito, configurando assim uma condicional. Ficando atento para a palavra-chave “pois”, onde a mesma trocará a ordem dos termos dentro da condicional, temos:
Se o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino, então a escola não prepara com eficácia o jovem para a vida.
Separando:
P: o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino
Q: a escola não prepara com eficácia o jovem para a vida
Como se trata de uma condicional, temos um valor lógico verdadeiro para (P-->Q).
Resposta: Certa.
A questão está certa. Discordo da Gisele e do comentário do professor. Concordo com o Eleizomar.
POIS determina que a segunda parte é a causa. De fato existe uma relação de condicional.
“A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino”
P -> Q
P: o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino
Q: A escola não prepara com eficácia o jovem para a vida
Se o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino, então a escola não prepara com eficácia o jovem para a vida.
Outro raciocínio:
A falta do ensino profissionalizante é a causa, uma condição suficiente para que o jovem não seja preparado com eficácia.
Sempre que uma condição é suficiente, temos uma relação de condicional: A -> B, sendo
A: a condição
B: a consequência
Nesse caso, eu diria que a conjunção coordenativa explicativa pode se desdobrar em uma condicional sim. Vejam bem:

Se ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino --->então a escola não prepara com eficácia o jovem para a vida.

PORTANTO, FIQUEM LIGADO COM CERTAS CONJUNÇÕES, COMO O "POIS"

Bons estudos, e que Deus vôs acompanhe!!!
Concordo com o comentário do elziomar, peço para o Professor verificar seu comentário, e , se necessário, alterá-lo pf
em primeiro vem a causa e depois a consequencia.

matéria sem vergonha! até o professor se enrola.
Porque não ~P -> ~Q ?? alguém??
Tiago, também poderia ser ~P ---> ~Q ( se ele considerasse P como sendo "a escola prepara com eficácia o jovem para a vida" e Q "o ensino profissionalizante faz parte do currículo da grande maioria dos centros de ensino").
Mas como a questão fala que "estaria corretamente representada por P ---> Q, em que P e Q fossem proposições lógicas convenientemente escolhidas", subentendesse que o examinador escolheu as proposições como P sendo "a escola NÃO prepara com eficácia o jovem para a vida" e Q "o ensino profissionalizante NÃO faz parte do currículo da grande maioria dos centros de ensino".
Deixando, assim, o gabarito CERTO.
Espero ter ajudado
“SE A escola não prepara com eficácia o jovem para a vida, ENTÃO pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino”
PARA A CESPE ''POIS'' PASSA IDEIA DE CONDICIONAL (se...então...)

GABARITO CORRETO
Sempre que, toda vez que, quando, como e pois equivalem-se ao operador lógico "se... então" da condicional, portanto a substituição ficaria representada da seguinte forma:
Se o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino, então a escola não prepara com eficácia o jovem para a vida.
Gabarito: Certo
Bom estudo!
E ai galera!

Só pra constar, a questão está certa! O impressionante é, além dos comentários errados de algumas pessoas, um professor comentar erroneamente essa questão! Isso é um absurdo, mas enfim.

Eu não sei se estou certo em meu raciocínio, mas, acredito que a questão esteja certa pelo seguinte motivo: a conjunção "pois" troca a ordem do termo "antecedente" pelo termo "consequente". Como assim?

O termo "antecedente" vem acompanhado pela expressão "SE", ou seja, ele é a condição suficiente (a causa). Já o termo "consequente" vem acompanhado pel expressão "ENTÃO", ou seja, ele é a condição necessária (a consequência).

Ou seja, toda vez que, em uma condicional, tivermos a conjunção "pois", esses termos, antecedente e consequente, estarão alterados. Veja de novo a proposição da questão:

- “A escola não prepara com eficácia o jovem para a vida (é a consequência e acompanha o ENTÃO; é o "Q"), pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino (é a causa e acompanha o SE; é o "P")”.

Perceberam que os termos estão trocados? Logo, se fossemos representar a proposição corretamente, teríamos que representá-la por P->Q, onde a ordem original das proposições seriam retomadas e, aí, teríamos que, SE o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino (P), ENTÃO a escola não prepara com eficácia o jovem para a vida (Q)".

Notaram que, quando eu tenho a conjunção "pois", a representação, ou seja, os seus termos ficam invertidos (Q->P), mas, ao representar essa proposição com a condicional "se.. então", esses termos voltam para posição original (P->Q)?

Espero ter ajudado!

FOCO NA MISSÃO!
A banca já fez questão parecida dando um resultado diferente. Na época da prova entraram com recurso alegando isso, mas não sei qual foi a resposta. ".
Por que ~P => ~Q estaria errado?
“A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino”
O se está do lado do pois --------Pois = se.
~Q→~P é equivalente à P→Q.
Além do mas, a questão diz: em que P e Q fossem proposições lógicas convenientemente escolhidas.
podem caracterizar uma condicional : QUANDO, COMO, PONTANTO, LOGO, POIS , PORQUE, eu fiz uma musica nao esqueço mais!! rsrsrs
Se a escola não prepara com eficácia o jovem para a vida, então o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino.
P -> Q
QUESTÃO CORRETA
Já resolvi questões com o POIS sendo condicional invertido, já essa não. Como vou diferenciar? é foda.
Exatamente Gabriel Almeida!!!!!!!
Em todas as questões o "pois" e seus sinônimos iniciam uma "inversão" para o Cespe!!!
Mas, nesse caso, eu posso chamar de P--> Q ; Q -->P; A --> B; B -->A... Qualquer joça rsrs
Obrigadinha!!!! ;) ;)
Já resolvi questões com o POIS sendo condicional invertido, já essa não. Como vou diferenciar?
P e Q fossem proposições lógicas convenientemente escolhidas.
Questão não marcou qual letra era cada proposição,portanto, neste caso tanto faz a posição. Só entenda que pois tem sentido de - Se..então.
Gabarito: CERTO
Comentário do Professor:
Separando e reescrevendo convenientemente a frase “A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino” e ficando atento para a palavra-chave “pois”, temos:
Reescrevendo: Se a escola não prepara com eficácia o jovem para a vida, então o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino
Separando:
P: a escola não prepara com eficácia o jovem para a vida
Q: o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino
Como se trata de uma condicional, temos um valor lógico verdadeiro para (P?Q), logo a resposta é certa.
Vi alguns comentários equivocados, pois para a banca CESPE é sim condicional invertido.
Portanto: Se o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino então a escola não prepara com eficácia o jovem para a vida.
Logo, como a questão diz que P e Q deverão ser convenientemente escolhidas, então fazemos:
P: o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino
Q:a escola não prepara com eficácia o jovem para a vida.
e temos P->Q
Seguinte, em regra, onde tem CAUSA e CONSEQUÊNCIA, da pra fazer uma condicional.
Pra saber as relações de causa e consequência tem que pegar uma perninha la do português, são várias as conjunções que cumprem essa tarefa, o pois é, mas nem sempre, uma delas.

A causa é sempre a condição suficiente e a consequência é sempre a condição necessária.
Mais uma pra anotar
Sinônimos do se, então " →, condicional"

- É uma consequência

- Se.., (Se, e depois a vigula)

- Como...,

- Quando...,

-Sempre que...,

- Consequentemente

- Pois (ordem invertida)
Não precisaria ter i sinal de não antes delas? Porque é uma negação
MTA ATENÇÃO:
Não é pq tem a palavra "NÃO" que é uma negação.
Felipe Frosi, essa informação que a banca coloca:

em que P e Q fossem proposições lógicas convenientemente escolhidas.

Justamente é para deixar claro que o "não" não importa na questão, pois ela não "batizou" quem são P e Q, veja dois exemplos

1) A menina pulou na grama e o menino não cantou , pode ser representada por P^Q em que P e Q fossem proposições lógicas convenientemente escolhidas. - CORRETO

2) agora com as proposições "batizadas" :

P: a menina pulou na grama

Q: O menino cantou

A menina pulou na grama e o menino não cantou , pode ser representada por P^Q - ERRADO, pois aqui a questão "batizou" o Q, aí deveria ser P^~Q

espero ter ajudado!
Aprendi errando que pois é implicação! Essa eu acertei!
Tão bom ver a evolução da gente em RLM kkkkk

A questão só disse se que eram convenientemente escolhidas, não marcou antes as proposições.
pois = se...então...

SE a escola não prepara com eficácia o jovem para a vida, ENTÃO o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino.

P=a escola não prepara com eficácia o jovem para a vida

Q= o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino.

logo, P->Q

RESPOSTA CORRETA
Se fosse avaliar pelo português, a conjunção "pois" pode ter valor conclusivo ou explicativo, mas não de condição. Vai entender esse RLM....
Concordo contigo.

Mas não é português, e lá realmente a questão estaria errada, rs.
Se o ensino fizesse parte do currículo... então a escola prepararia com eficácia o jovem para a vida.
conectivo POIS....SINÕNIMO SE ENTAO.
GABARITO CORRETO
"Pois" = Inversão do "Se, então".
Se o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino, então a escola não prepara com eficácia o jovem para a vida.
"Se não puder se destacar pelo talento, vença pelo esforço".
Complementando os comentários dos colegas:
- Sinônimos do conectivo ''se..então'' para a banca CEBRASPE: Quando, portanto, como, logo, desde que (inversão), sempre, todo, somente se, pois (invertido).
- ATENÇÃO: Cuidado com o termo “é consequência de”. Para ser condicional, deve ter dois verbos: um antes e outro depois. Exemplo: Passar é consequência de estudar.
Bons estudos!
Sem mimimi a questão quer saber se o enunciado pode ser representado por P->Q
ela não mencionou quem era P ou quem era Q, então concluímos que Q e P pode estar em qualquer ordem

ID

965140

Banca

CESPE / CEBRASPE

Órgão

ANS

Ano

2013

Provas

CESPE - 2013 - ANS - Analista Administrativo

Disciplina

Raciocínio Lógico

Assuntos

Com relação às proposições lógicas, julgue os próximos itens.

A expressão “Como não se indignar, assistindo todos os dias a atos de violência fortuitos estampados em todos os meios de comunicação do Brasil e do mundo?” é uma proposição lógica que pode ser representada por P -> Q , em que P e Q são proposições lógicas convenientemente escolhidas.

Alternativas

Certo

Errado

Comentários

Errada,

não pode ser uma proposição lógica por ser uma sentença interrogativa.

Lembrar: Sentenças interrogativas não são proposições!!

Complementando o comentário do colega acima:

Não é proposição lógica	É proposição lógica...
Sentenças imperativas	Sentença declarativa
Ex. Vá ao aeroporto.	(avaliadas em V ou F, nunca em ambos)
Sentenças interrogativas
Ex. Quantos cachorros você tem?
Sentenças exclamativas
Ex. Quanta coisa legal!
Sentenças optativas
Ex. Feliz natal! Parabéns!
Sentenças abertas
Ex. Ele é jogador de futebol (ele quem?); A cidade é bonita (que cidade?)
Paradoxos
Ex. Um homem diz que está mentido. Ele diz a verdade, ou ele mente?

Minha única dúvida é em relação a essas "sentenças abertas" aí... no comentário da Thaís
Lembrando que para ser uma proposição lógica, a sentença nunca poderá ser:
Imperativa, interrogativa, exclamativa, aberta, paradoxo e optativa.
Para ser uma preposição lógica, a sentença deverá ser declarativas.
Logo, como a sentença do enunciado não é declarativa e sim interrogativa, a resposta é errado.
Errado, sentença interrogativa! Não podemos atribuir valor lógico.
Gabarito. Errado.
sentenças interrogativas não possuem valores lógicos.

BONS ESTUDOS!!!!
Muito boa sua explicação Layse.
Não tenho muito que acrescentar aos comentários dos colegas, apenas esclarecendo que uma proposição é uma declaração na qual podemos sempre atribuir um valor lógico a mesma, ou Falso ou Verdadeiro.
Lembrar dos princípios basilares:
Princípio da Identidade ---> Se uma proposição é verdadeira então ela é logicamente verdadeira, se for falsa então será logicamente falsa.
Princípio do terceiro excluído ---> Uma proposição só pode ter dois possíveis valores lógicos, V ou F não podendo existir um terceiro.
Princípio da não contradição ---> Uma proposição não pode ser verdadeira e falsa simultaneamente.
Complementando: declaraçoes interrogativas, exclamativas, sem verbo, verbos no imperativo e sentenças abertas nao representam UMA PROPORSIÇAO SIMPLES. APENAS PARA REFORÇAR.
A questão acima não representa uma proposição.
Não há proposições em frases:

Interrogativas; Ex: Como é o seu nome?, O jogo foi quanto?
Exclamativas; Ex: Feliz aniversário!
Imperativas (Com sentido de ordem); Ex: Faça isso! , Estude mais!, Leia aquele livro.

Toda proposição deve:
Ser uma oração com sujeito e predicado;
Possuir valores lógicos, ou seja, Verdadeiro ou falso;
Ser declarativa, ou seja, não pode ser interrogativa, exclamativa e nem imperativa.
Não é proposição:

sentenças abertas -> Ex: x+2=5 (uma vez que não se sabe o valor de x)
perguntas?
exclamações!
ordens
Viu "interrogação"? Esquece preposição. Ah, vale também para "exclamação"!
alguem saberia me dizer o que significa proposicoes logicas convenientemente escolhidas? nao entendo este convenientemente...
Perguntas, exclamações, ordens, sentenças abertas, não são preposições!
Sentença aberta, não tem como valorar.
Errada
Frases interrogativas não são proposições.
Lembrando que para ser uma proposição lógica, a sentença nunca poderá ser:

Imperativa, interrogativa, exclamativa, aberta, paradoxo e optativa.

Para ser uma preposição lógica, a sentença deverá ser declarativas.

Logo, como a sentença do enunciado não é declarativa e sim interrogativa, a resposta é errado.

PROFESSOR QC
Essa foi dada. O problema é quando for exclamativa que dependendo do contexto pode ser considerada também uma proposição.
https://www.youtube.com/watch?v=dTpx65YVLOY
Melhor que ficar dependendo de regra Neymar, ou da amante... ou quaisquer outras.
Gabarito: ERRADO
Não são preposições:
==> Imperativa, interrogativa, exclamativa, aberta, paradoxo e optativa
Nas frases interrogativas não são preposições lógicas, sendo assim, não pode ser representada por P→Q.
Fonte: ESTRATÉGIA CONCURSOS
Bizu que peguei aqui no qc:

NÃO são proposições -> "PESO"

Perguntas
Exclamações
Sentenças abertas
Ordem
primeiramente não é nem proposição kkkkkkkkkkkkk
ERRADO

PESO não são proposições
Pergunta
Exclamação
Sentença aberta (ex: x+2= 3 - desde que não seja definido o valor de x)
Ordem
ERRADO,
NÃO é sequer uma proposição.

❌ FRASES INTERROGATIVAS
❌ FRASES EXCLAMATIVAS
❌ FRASES ABERTAS
❌ PARADOXOS
INTERROGATIVA NÃO É PROPOSIÇÃO

fonte: Jhoni Zini

ID

971446

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Nos termos do Edital n.º 9/2012 – DGP/DPF, de 10/6/2012, do concurso público para provimento de vagas no cargo de escrivão de polícia federal, cada candidato será submetido, durante todo o período de realização do concurso, a uma investigação social que visa avaliar o procedimento irrepreensível e a idoneidade moral inatacável dos candidatos. O item 19.1 do edital prevê que a nomeação do candidato ao cargo fica condicionada à não eliminação na investigação social e ao atendimento a outros requisitos. Com base nessas informações, e considerando que Pedro Henrique seja um dos candidatos, julgue o item seguinte.

Considere que sejam verdadeiras as proposições “Pedro Henrique não foi eliminado na investigação social" e “Pedro Henrique será nomeado para o cargo". Nesse caso, será também verdadeira a proposição “Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo".

Alternativas

Certo

Errado

Comentários

Consideramos segundo a questão:
"Pedro Henrique não foi eliminado na investigação social" = V
"Pedro Henrique será nomeado para o cargo" = V

Logo, na proposição “Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo” temos F -> F = V

Considerando a proposição "PH não foi eliminado na investigação social" como P e "PH será nomeado para o cargo" como Q, ambas verdadeiras. Então a proposição " Se PH foi eliminado na investigação, então ele não será nomeado para o cargo", ~P - > ~Q, será verdadeira, pois na condicional ambas alternativas falsas torna a proposição verdadeira. Veja tabela verdade.

P	Q	~ P	~Q	~P -> ~Q
V	V	F	F	V
V	F	F	V	V
F	V	V	F	F
F	F	V	V	V

Resolução:

já que a pergunta diz que a proposiçao é verdadeira :

~E: Pedro Henrique não foi eliminado na investigação social
N: Pedro Henrique será nomeado para o cargo

Então ficaria assim:
   v      v
~E ^ N         v    * Na conjunção para ser verdadeiras todas as premissas devem serem verdadeiras também

f        f
E --> N v    * Na condicional para ver falso a proposiçaõ deve ser v -> f como as duas premissas são falsas logo seu valor será verdadeiro

Resposta Certa
Considere que sejam verdadeiras as proposições “Pedro Henrique não foi eliminado na investigação social” e “Pedro Henrique será nomeado para o cargo”. Nesse caso, será também verdadeira a proposição “Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo”.

primeira sentença verdadeira ok conforme o enunciado

segunda sentença é uma negagação verdadeira Se Pedro foi eliminado não será nomeado (isso é a mais pura verdade) Lógica
P1: “Pedro Henrique não foi eliminado na investigação social”

P2: “Pedro Henrique será nomeado para o cargo”

P3: “Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo”.

p: Pedro Henrique foi eliminado na investigação social,

q: ele não será nomeado para o cargo.

Aqui, P3 é uma condicional, logo, vemos que no mesmo p é falso, então, independentemente do valor lógico de q, P3 será verdadeiro.

A resposta é: Certo.
"~P" "P"
P=>~Q
F => F = V
Pedro Henrique não foi eliminado na investigação social      ^            Pedro Henrique será nomeado para o cargo
                         VERDADEIRA                                                                               VERDADEIRA

Se Pedro Henrique foi eliminado na investigação social,        ---->                então ele não será nomeado para o cargo.
                        FALSA                                                                                                   FALSA

Tabela do Se...então
V ---> V   = V
V ---> F =   F
F ---> V = V
F ---> F = V
essa f[

fácil dmais
Pedro Henrique não eliminado = V
Pedro Henrique eliminado = F

Já mata a questão = V

Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo
não foi eliminado ( ~ I ) = V

nomeado ( N ) = V

I se então ~ N

F se então F = V
p = Pedro Henrique não foi eliminado na investigação social; (V)

q = Pedro Henrique será nomeado para o cargo; (V)

p -> q (só será falso se: p = Verdadeiro; q = Falso)

Proposição proposta: “Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo.”

Pedro Henrique foi eliminado na investigação social; (F)

Pedro Henrique não será nomeado para o cargo; (F)

F -> F = Verdadeiro

GABARITO: CERTO
Só lembrar que a condicional é falso quando for "Vera Fischer".
CORRETO: Pois a primeira proposição era falsa, haja vista ser uma negação da proposição “Pedro Henrique não foi eliminado na investigação social”. E sendo falsa a primeira, toda frase será verdadeira.
Lembrem que se em uma proposição condicional (A -> B), a primeira proposição for falsa, toda a frase será verdadeira, independente do conteúdo da segunda.
CERTO
TRADUZINDO:

Ele será nomeado se ele não for eliminado!

Se ele for eliminado , então ele não sera nomeado.
Ambas são proposições verdadeiras:

p: Pedro Henrique não foi eliminado na investigação social
q: Pedro Henrique será nomeado para o cargo

Agora, veja a proposição dada: “Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo”. Ela pode ser reescrita como: ~p → ~q.
Como p=V e q=V, essa condicional fica: F → F (que é verdadeiro).

Alternativa CORRETA.
SE PEDRO FOI ELIMINADO, ENTÃO NÃO SERÁ ELIMINADO.

P-->Q

F-->F = VERDADE

GABARITO= CORRETO
P ->Q(V ->V), se as negamos: ~P-> ~Q( F - >F) continua sendo verdadeira a implicação.
A única linha em que as proposições P e Q são verdadeiras, tem como ~P->~Q verdadeira, também:

| P | Q | ~P | ~Q | ~P->~Q |
| V | V | F | F | V |
Que venha assim na minha prova, amém kkk
O cuidado com a questão é assumir que p1 e p2 são verdadeiras. Não comece pelo teste da conclusão falsa, pq eu errei assim
VAMOS LA.
“Pedro Henrique não foi eliminado na investigação social" VERDADEIRO
Pedro Henrique foi eliminado na investigação social FALSO.

não precisamos nem olhar o restante!
o precedente sendo FALSO, qualquer valor lógico do CONSEQUENTE fará a sentença ser Verdadeira.
NA CONDICIONAL, ¨F¨ DE FLAMENGO, NA FRENTE, SEMPRE SERÁ VERDEIRO.
Na condicional,se o antecedente for F,todo o resto será verdadeiro F>>F=Falsa
Essa questão poderia ser resolvida rapidamente com o seguinte: SEMPRE que o ANTECEDENTE DE UMA CONDICIONAL FOR (F) , não importa o restante,pois o resultado da proposição composta será VERDADEIRO GABARITO = C
Minha contribuição.

Tabela Verdade da Condicional:

V -> V = V
V -> F = F
F -> V = V
F -> F = V

Abraço!!!
Nega e mantem=Neymar
“Pedro Henrique não foi eliminado na investigação social" (V)
P

“Pedro Henrique será nomeado para o cargo" (V)
Q

“Se Pedro Henrique foi eliminado na investigação social, então ele não será nomeado para o cargo".

~P ------> ~Q = V
F---------- F

GABA: CORRETO uma vez que também será verdadeira a proposição proposta pela banca.
Pedro Henrique não foi eliminado na investigação social = V
Pedro Henrique será nomeado para o cargo = V
Se Pedro Henrique foi eliminado na investigação social (F), então ele não será nomeado para o cargo (F).
F -> F = V

ID

971458

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2013

Provas

CESPE - 2013 - Polícia Federal - Escrivão da Polícia Federal

Disciplina

Raciocínio Lógico

Assuntos

Suspeita-se de que um chefe de organização criminosa tenha assumido as despesas de determinado candidato em curso de preparação para concurso para provimento de vagas do órgão X. P1: Existe a convicção por parte dos servidores do órgão X de que, se um chefe de organização criminosa pagou para determinado candidato curso de preparação para concurso, ou o chefe é amigo de infância do candidato ou então esse candidato foi recrutado pela organização criminosa para ser aprovado no concurso; P2: Há, ainda, entre os servidores do órgão X, a certeza de que, se o candidato foi recrutado pela organização criminosa para ser aprovado no concurso, então essa organização deseja obter informações sigilosas ou influenciar as decisões do órgão X. Diante dessa situação, o candidato, inquirido a respeito, disse o seguinte: P3: Ele é meu amigo de infância, e eu não sabia que ele é chefe de organização criminosa; P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou. Considerando essa situação hipotética, julgue os itens subsecutivos.

Com fundamento nas proposições P1, P2, P3 e P4, confirma-se a suspeita de que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso.

Alternativas

Certo

Errado

Comentários

Errado.
Obserque que na estrutura P1, a proposição A é Falso, logo o resultado da condicional será Verdadeiro, e não tem-se como confirmar o valor de C, já que a proposição será Verdadeira.
Não confimando C, não há como confirmar a premissa P2: C -> (D V E) : ?
Logo, não há o que se concluir ( D v E ), questão errada.
Pela preposição P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou é possível inferir que o chefe da organização criminosa não custeou o curso de preparação para o concurso do candidato, uma vez que é informado que "ele (chefe da organização criminosa) não pagou".

A preposição P4 pode ser quebrada em:

P = Pedi a ele que pagasse meu curso de preparação
Q = Ele não pagou

logo, como a palavra "mas" é uma conjunção, podemos representar a preposição P4 como:

P4: P ^ Q

e como P4 é verdadeiro então podemos concluir que P ^ Q necessariamente tem que ser verdadeiro e a única forma de P ^ Q ser verdadeiro é P (Pedi a ele que pagasse meu curso de preparação) ser verdadeiro e Q (Ele não pagou) também ser verdadeiro. Chegando a conclusão que o chefe da organização criminosa não pagou.
Como vc sabe que a P4 é verdadeira, se a questão não afirma isso...

obg
Essa questao foi bem dificil,Respondendo ao amigo Reginaldo,Por se tratarem de premissas,P1,P2,P3 e P4. Quando a questao não explicitar deve-se deduzir que a ultima premissa é a conclusão,no caso P4 é a conclusão,partindo da idéia que todas as premissas devem ser consideradas verdadeiras,deve se buscar os valores logicos das proposiçoes que estao dentro das premissas,com isso vc conseguira ver que a P4 é falsa,fazendo com que a P4 seja uma contradição,por não concordar em valor que deveria ser verdadeiro,putz é dificil explicar,espero que tenha ajudado em algo,se não ajudou em PN eu entendo,é foda mesmo!
Luciano Pereira,

Posso estar enganado, mas acho que não é por ai. Olha a pergunta da questão:

"Com fundamento nas proposições P1, P2, P3 e P4, confirma-se a suspeita de que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso."

Ele perguntou com fundamento nas 4premissas e não só na P4. E como não dá pra valorar os itens da P2, não tem como confirmar se o chefe da organização criminosa pagou não, sendo assim a questão é ERRADA.
Considerando essa situação hipotética, julgue os itens subsecutivos.

Antes de resolvermos os itens abaixo, vamos fazer uma pequena análise das proposições P1, P2, P3 e P4.

A premissa P1 é uma proposição composta do tipo se A então (B ou C), onde
A: um chefe de organização criminosa pagou para determinado candidato curso de preparação para concurso;
B: o chefe é amigo de infância do candidato;
C: esse candidato foi recrutado pela organização criminosa para ser aprovado no concurso

A premissa P2 é uma proposição composta do tipo (se D então (E ou F)), onde
D: o candidato foi recrutado pela organização criminosa para ser aprovado no concurso
E: essa organização deseja obter informações sigilosas
F: influenciar as decisões do órgão X

A premissa P3 é uma proposição composta do tipo (G e H), onde:
G: Ele é meu amigo de infância
H: eu não sabia que ele é chefe de organização criminosa

A premissa P4 é uma proposição composta do tipo (I e J), onde:
I: Pedi a ele que pagasse meu curso de preparação
J: ele não pagou

As tabelas verdade citadas na resolução dos itens são:

CONDICIONAL
A B se A então B
V V V
V F F
F V V
F F V
(Se A então B ) só é valorada como “F” quando A for valorada como “V” e B for valorada como “F”. Nos demais casos, o resultado é sempre “V”.

CONJUNÇÃO
A B A e B
V V V
V F F
F V F
F F F
(A e B ) só é valorada como “V” quando A for valorada como “V” e B for valorada como “V”. Nos demais casos, o resultado é sempre “F”.
Com fundamento nas proposições P1, P2, P3 e P4, confirma-se a suspeita de que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso.

ERRADO - Para resolvermos este item, devemos observar se a conclusão é consequência das premissas, supondo que essas premissas sejam simultaneamente verdadeiras, independente dos respectivos conteúdos.

Sendo assim, para que se confirme a suspeita de que o chefe de uma organização criminosa tenha custeado para o candidato curso de preparação para o concurso, seria necessário que, na premissa P1, a proposição A fosse valorada como V.
No entanto, não se pode afirmar que a proposição A é “V” uma vez que, para que a premissa P1 seja valorada como “V”, tanto faz se a proposição A for “V” ou“F” (veja a tabela verdade do se A então B ).
Além disso, para que premissa P4 seja valorada como “V”, tanto I quanto J devem ser valoradas como “V” (veja a tabela verdade de conjunção) e a proposição J afirma o seguinte: “ele não pagou”
P1: Existe a convicção por parte dos servidores do órgão X de que, se um chefe de organização criminosa pagou para determinado candidato curso de preparação para concurso, ou o chefe é amigo de infância do candidato ou então esse candidato foi recrutado pela organização criminosa para ser aprovado no concurso;
p: um chefe de organização criminosa pagou para determinado candidato curso de preparação para concurso,
q: o chefe é amigo de infância do candidato
r: então esse candidato foi recrutado pela organização criminosa para ser aprovado no concurso;
P2: Há, ainda, entre os servidores do órgão X, a certeza de que, se o candidato foi recrutado pela organização criminosa para ser aprovado no concurso, então essa organização deseja obter informações sigilosas ou influenciar as decisões do órgão X.
s: essa organização deseja obter informações sigilosas ou influenciar as decisões do órgão X.
P3: Ele é meu amigo de infância, e eu não sabia que ele é chefe de organização criminosa;
t: eu não sabia que ele é chefe de organização criminosa;
P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou.
C: “A organização deseja obter informações sigilosas ou influenciar as decisões do órgão X”.
Escrevendo em símbolos lógicos:
P1: p→(q v r)
P2: r→s
P3: q^t
P4: ^~p
C: conclusão
Considerando a proposição P3 como verdade, q é verdadeira, logo em P1, isso levaria r ser falsa, por se tratar de uma disjunção exclusiva, assim, levaria a conclusão que (q v r) é verdade.
Mas como P1 é uma condicional, não podemos concluir o valor lógico de p, isso nos leva a resposta: Errado.
PEDI PARA PAGAR, MAS ELE NÃO CUSTEOU
V ^ V = VERDADEIRO

GABARITO ERRADO
A questão conversou demais, porém muito simples. O candidato foi claro em suas palavras:

P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou.
V ^ V = V
Partindo do pressuposto que a proposição P4 seja falsa, o valor lógico de P (o qual o professor disse que não tem como atribuir) passa a ser verdadeiro. Todas as premissas serão verdadeiras e a conclusão falsa, logo o argumento é inválido.
Típica questão pra deixar em Branco e economizar tempo p as de mais.
Enunciado Grande para fazer o candidato perder tempo, porém a questão é simples... Vc mata pela conclusão e pela preposição P4 que inválida tudo
Como nso se pode confirmar P2, nao se pode concluir que seja uma conclusao valida. A alegacao de muitos de que a questao traz P4 como verdadeira, pelo simples fato de ser premisssa, nao tem nada haver, senao basta considerar tudo o que for premissa como verdadeiro e nunca haverá nada para se fazer.
Está errado porque nao é possível avaliar a validade do argumento, ja que pelo métodos das premissas verdadeiras ou pelo método das premissas verdadeiras e conclusao falsa nao é possível definir se a premissa 2 é F ou V. Portanto, nao é possivel chegar a conclusao que afirma a questao.

GABARITO: E.
GAB: Errado

Com fundamento(com base nelas ou confiando nelas) nas proposições P1, P2, P3 e P4, confirma-se a suspeita de que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso. Não confirma-se a suspeita.

Partindo do pressuposto que as premissas são verdadeiras então: P1, P2, P3 e P4 são verdadeiras.
Só a P4 responde a questão

P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou. (V)

Variações do conectivo E: mas / nem.

Na conjunção (E) para ser verdadeira, todas as proposições tem que ser verdadeira.
Aqui a questão traz “p” como conclusão para as premissas. Vamos forçá-la ser falsa e, se as premissas puderem se tornar verdadeiras, esse argumento será inválido e nada se pode concluir. Portanto: p = F.

P4: y ^ V. Para ser verdadeira: y = V.

P3: q ^ w. Para ser verdadeira: q=V e w=V.

P1: F → q v r. A condicional já é verdadeira, independente de q v r.

P2: r → s v t. As letras podem assumir qualquer valor. Logo, a premissa pode ser tornada verdadeira.

Assim, concluímos que a partir de uma conclusão falsa, as premissas tornam-se verdadeiras. O argumento é inválido e não é possível afirmar que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso.

Alternativa ERRADA.
Percebi que atribuindo V ou F à P4, a assertiva será sempre errada.
Olha, fico realmente chateada com o CESPE.
A proposição P1 dessa questão é simbolizada como

P-->(Q v R)

Nessa outra questão, foi escrita da mesma maneira com o início SE e no final com o ENTÃO.
“Se Josué foi aprovado no concurso e mudou de cidade, então Josué mudou de emprego”

E ficou simbolizada como (P /\ Q)--> R

Po, assim fica difícil... alguém sabe o motivo?
Ele não pagou
Não se trabalha com hipóteses e como a questão não deu indícios de que o chefe da ORCRIM pagou, então GAB: E
Só lendo as premissas já se sabe que o chefe não pagou.
Como a questão não informou qual é a conclusão, considera-se P4 como conclusão. Então P4 é considerada VERDADEIRA.

Para que P4 seja verdadeira, temos
Pedi a ele que pagasse o curso (A), mas(e) ele não pagou (B) [ representando: A ^ B ]

Para que a proposição A ^ B seja verdadeira é necessário que as duas sejam verdadeiras, portanto A(V) ^ B(V) = V

Se B é verdadeira e diz que "ele NÃO pagou", então afirmar que o chefe da organização criminosa pagou o curso para o candidato é FALSA.

Ou seja, não podemos confirmar a suspeita de que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso.

###Não tenha medo de "perder" (gastar) tempo entendendo como chegar à resposta, pois só assim você aprenderá!

Vamos juntos
Questões longas, com texto grande do Cespe, geralmente trazem as respostas nas próprias proposições BASTA INTERPRETAR OS TEXTOS para ser mais rápido e objetivo na hora da prova:
Questão:
Com fundamento nas proposições P1, P2, P3 e P4, confirma-se a suspeita de que o chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso.

P1: Confirma
P2:Confirma
P3: Ele é meu amigo de infância, e eu não sabia que ele é chefe de organização criminosa.

Veja que a proposição confirma a suspeita de um suposto chefe de organização criminosa, mas em nenhum momento cita o custeamento de curso de preparação para concurso como em P1, P2 e P3 confirmam.

P4: Confirma

Logo a questão está errada.
Essa questão é do tipo 2A (pra quem está estudando com direção)---- classificação

vem 3 tipos de conectotes

e-----> verdadeiro
se então -------> falso
ou ou------> falso

daí vai deixando as premissas verdadeiras e falsas segundo os conectores.
Pedi a ele que pagasse meu curso de preparação, mas ele não pagou.
MAIS UM POUCO E A GENTE ESTÁ RESOLVENDO UMA QUESTÃO DE MATEMÁTICA
Aquele tipo de questão que vale a pena deixar em branco... meia hora pra responder errado... fala sério... acertar o resto já é suficiente.
Força e Honra!
A resposta está na P4.
P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou.
(P ^ ~Q) =
Conclusão: O chefe de organização criminosa tenha custeado para o candidato curso de preparação para o concurso. => (Q) =

para a premissa 4 ser verdadeira, Q(conclusão) deve ser falsa.
(P ^ ~Q) = V
(Q) = F
P1 não deveria ser (a → vb vc) ?
Questão mal elaborada. Você tem que adivinhar que P4 é a conclusão.
Matei a questão pelo final: P4: Pedi a ele que pagasse meu curso de preparação, mas ele não pagou
português kkkkk interpretação de texto

ID

975109

Banca

UEPA

Órgão

PC-PA

Ano

2013

Provas

UEPA - 2013 - PC-PA - Papiloscopista Policial

Disciplina

Raciocínio Lógico

Assuntos

Considere as proposições seguintes:

p: Paulo apresentar uma queixa

q: o Delegado investigará

r: Ricardo será preso

A linguagem simbólica da proposição composta “Não é o caso em que,se Paulo apresentar uma queixa, então, o delegado investigará e Ricardo será preso” é:

Alternativas

~[ p ↔( q Λ r ) ]

~[ p → (q Λ r ) ]

~[ p V (q Λ r ) ]

~[ p Λ (q V r ) ]

~[ p → (q V r ) ]

Comentários

Quando a questão colocou a condicionante "se" => ja ficariamos entre as alternativas b e e. Agora se ele for investigado independentemente da probablidade de comprovarem ele será preso. por isso que deve terem eliminado os parenteses... por nao terem que comprovar a veracidade, ai ficaria assim se ele for investigado sera preso, portanto alternativa B.
Romeu da uma olhada nessa blz
Não entendi bolhufas de nada, não seria ~[p>(q ^ r)] ? alguém poderia me explicar?
pessoal, só pra avisar. o site "questão de concurso" errou nessa questão.
A alternativa "b" é:
~[ p-> (q ^ r) ] e não ~[ p (q → q Λ r ) ]
já confirmei na prova
Erro de digitação do site!

Na prova a alternativa b é: ~[ p-> (q ^ r) ]
~[ p -> (q ^ r) ]
Gabarito. B.
é só se ligar nos conectivos.
De acordo com o enunciado e utilizando a linguagem simbólica, tem-se:
“Não (~) é o caso em que,se Paulo apresentar uma queixa (p), então (→) , o delegado investigará (q) e (Λ) Ricardo será preso (r)”

Assim, ~[ p → (q Λ r ) ]

Resposta B)
Não é o caso em que,se Paulo apresentar uma queixa, então, o delegado investigará e Ricardo será preso

~[ p → (q Λ r ) ]

esta negando ~

P-->= SE ENTÃO

Q = DELEGADO

R= RICARDO

E = ^

AGORA MONTA

~[ p → (q Λ r ) ]

GABARITO= B

ID

1004506

Banca

CESPE / CEBRASPE

Órgão

DETRAN-ES

Ano

2010

Provas

CESPE - 2010 - DETRAN-ES - Assistente Técnico de Trânsito

Disciplina

Raciocínio Lógico

Assuntos

Considerando a sentença “sempre que um motorista passar em excesso de velocidade por um radar, se o radar não estiver danificado ou desligado, o motorista levará uma multa”, julgue o item subsecutivo.

Se forem falsas as afirmações “o radar estava desligado” e “o motorista levou uma multa”, então a sentença “se um motorista passou em excesso de velocidade por um radar e este não estava danificado ou desligado, então o motorista levou uma multa” será verdadeira, independentemente dos valores lógicos das outras proposições simples que a compõem.

Alternativas

Certo

Errado

Comentários

ACREDITO QUE A QUESTÃO SEJA UM PROPOSIÇÃO SIMPLES.
Alguém mais pode contribuir?
(se um motorista passou em excesso de vel. por um radar e este ñ estava danificado ou desligado), (então o motorista levou uma multa)

(pode ser V ou F - não especificaram) (V - RADAR DESLIGADO É F)    (F)

Primeiro se faz a expressão (se um motorista passou em excesso de velocidade por um radar e este não estava danificado ou desligado)

se V e V = V

se F    e V = F

Então a primeira expressão poderá ser verdadeira ou falsa

Agora se faz a expressão como um todo

(se um motorista passou em excesso de vel. por um radar e este não estava danificado ou desligado), (então o motorista levou uma multa

(RESULTADO 1)     V -> F = F

(RESULTADO 2) F -> F = V

Então os resultados possíveis são verdadeiro ou falso, então a afirmação da questão está errada
“sempre que um motorista passar em excesso de velocidade por um radar ^ se o radar não estiver danificado ou desligado -->

V/F V/F F

o motorista levará uma multa.

F

Como é uma condicional que termina com F, só posso dizer que será sempre verdadeira se os demais derem como resultado F, se for V, será uma proposição falsa.
Professor Paulo Henrique do EuVouPassar, respondeu a assertiva:

Vamos 'quebrar' a proposição:

'um motorista passou em excesso de velocidade por um radar' = M1

'o radar estava danificado' = R1

'o radar estava desligado' = R2 = F

'o motorista levou uma multa' = M2 = F

Já que M2 = F e a proposição deve ser V (a questão diz isso...), então a 1ª parte da condicional deve também ser F (F -> F = V). Ou seja:

(M1 ^ ~(R1 v R2)) = F

=> (M1 ^ ~(R1 v F)) = F

Aqui, usaremos a técnica 'Advogado do Diabo': vamos provar o contrário que a questão nos pede!

Olha só, se tivermos M1 = V e R1 = F (valor lógicos possíveis), teremos:

V ^ ~(F v F)

= V ^ ~(F)

= V ^ V = V

Assim, a condicional ficaria V -> F = F, diferente do que a questão propôs.

Item errado.

At.te, CW.

https://www.euvoupassar.com.br/artigos/detalhe?a=quem-manda-e-voce-2011-parte-23
P: O motorista passou em excesso de velocidade por um radar
Q: O radar estava desligado
Z: O motorista levou uma multa

A sentença será representada pela seguinte forma:

(P ^ ~Q) ---> Z

Na questão diz que as preposições Q e Z são falsas, logo ficará da seguinte forma:

(P ^ V) ---> F

logo, para ela ser verdadeira, a preposição P tem que ser falsa. Caso a preposição P seja verdadeira, a sentença será falsa.

GAB. - E
P Q ~Q P-> ~Q
V V F F
V F V V
F V F V
F F V V

Logo,será incorreto.
se um motorista passou em excesso de velocidade por um radar e este não estava danificado ou desligado, então o motorista levou uma multa.

p ^ ( q V r ) ----->>>> s
ERRADO

P (motorista ..velocidade) Q (radar desligado-estragado) R (multa)

P v Q -> R

V F F
V -> F

EXISTE A POSSIBILIDADE DE SER FALSO.

ID

1012198

Banca

CESPE / CEBRASPE

Órgão

TCE-RO

Ano

2013

Provas

CESPE - 2013 - TCE-RO - Agente Administrativo

Disciplina

Raciocínio Lógico

Assuntos

A respeito da proposição “Após a maiúscula vitória da seleção brasileira de futebol sobre a França neste domingo, não há mais quem não aposte todas as suas fichas no sucesso da seleção canarinho na Copa das Confederações”, julgue os próximos itens.

Caso essa proposição seja verdadeira, a probabilidade de que algum torcedor não aposte todas as suas fichas no sucesso da seleção canarinho na Copa das Confederações é nula.

Alternativas

Certo

Errado

Comentários

CERTO!

Se a proposição diz que "não há mais quem não aposte todas as suas fichas no sucesso da seleção", é a mesma coisa que dizer: "todos apostam suas fichas no sucesso da seleção". Portanto, se essa proposição é verdadeira, então a probabilidade de que algum torcedor não aposte todas as suas fichas no sucesso da seleção na Copa das Confederações é mesmo nula.

Foco, força e fé!
A proposição no enunciado nos diz que "não há mais quem não aposte todas as suas fichas no sucesso da seleção", isso equivale a dizer que todo mundo aposta as fichas na nossa seleção.

Assim, se a proposição é tomada como verdadeira como diz o enunciado, teremos zero chance de algum torcedor torcer contra a seleção, pois 100% deles torcem a favor da mesma.

Logo a resposta é Certo.
Essa questão acaba sendo um peguinha para programador, pois vemos 0 como algo diferente de nulo.
Eu fiz assim:
P(AUB) = P(A) + P(B) <--- isso tem que dar 100% ou 1 já que a probabilidade varia de 0 a 1
Onde: P(A) = todos apostam todas as fichas
P(B) = alguém não aposta todas as fichas
Portanto:
1 = 1 + P(B)
P(B) = 1 - 1
P(B) = 0 (nulo)
NA CONDICIONAL SE FOSSE FF, A PROPOSIÇÃO NAO DARIA V
?
AINDA NAO ENTENDI :(
Quando nego duas vezes estou tornando a frase verdadeira,,, mera questão de interpretação, pelo menos foi assim que entendi
entendi assim: "...não há mais quem não aposte..." =todos

"...a probabilidade de que algum torcedor não aposte todas as suas fichas ..."

negação de quantificador:

1) nenhum, troca por algum

2) algum, troca por nenhum ou pelo menos um

3) todo , troca por algum ou pelo menos um ou existe
Gabarito: CERTO

-----

Fiz da seguinte forma:

Transformei o período numa proposição conjuntiva. Então ficou assim:

“Após a maiúscula vitória da seleção brasileira de futebol sobre a França neste domingo, não há mais quem não aposte todas as suas fichas no sucesso da seleção canarinho na Copa das Confederações”

-----

A seleção brasileira de futebol ganhou da França neste domingo E não há mais quem não aposte todas as suas fichas no sucesso da seleção canarinho na Copa das Confederações"

-----

A assertiva informa que a proposição é verdadeira, logo sabemos que na conjunção para ser verdadeira só temos um jeito: "V^V". Então se as duas proposições são verdadeiras, realmente, a probabilidade de que algum torcedor não aposte todas as suas fichas no sucesso da seleção canarinho na Copa das Confederações é NULA.
NEGAÇÃO DO "NENHUM" É "PELO MENOS UM"

"não há mais quem não aposte" = V

"a probabilidade de que algum torcedor não aposte todas as suas" = F
Se "não há mais quem não aposte" é porque "todos apostam". Se todos apostam, é nula a possibidade de algum não apostar.

Gab. Certo.
Questão bem feita... Sentei na graxa, mas identifiquei meu erro.

A qustão induz o candidato ao erro de pensar que se trata de proposição composta p -> q verdadeira

Seguindo nessa lógica, o candidato verifica que F -> F é verdadeiro, então a aposta geral pode ser falsa.

Na verdade trata-se de proposição simples e de interpretação direta. É o que está escrito mesmo. Todos vão apostar? Beleza, todos vão apostar...
questao desse tipo no cespe...ate fico desconfiado.
A proposição no enunciado nos diz que "não há mais quem não aposte todas as suas fichas no sucesso da seleção", isso equivale a dizer que todo mundo aposta as fichas na nossa seleção.

Assim, se a proposição é tomada como verdadeira como diz o enunciado, teremos zero chance de algum torcedor torcer contra a seleção, pois 100% deles torcem a favor da mesma.

Logo a resposta é Certo.

Qconcursos

ID

1013443

Banca

FUNDATEC

Órgão

PROCERGS

Ano

2012

Provas

Disciplina

Raciocínio Lógico

Assuntos

Dadas as proposições: p: “Ana é saudável.” q: “Paulo está gripado.”

Uma forma de se representar a proposição ~(p ^ ~q) em linguagem corrente é:

Alternativas

“Ana não é saudável e Paulo não está gripado.”

“Não é verdade que Ana não é saudável e Paulo não está gripado.”

“Ana não é saudável ou Paulo não está gripado.”

“Se Ana é saudável, então Paulo está gripado.”

“Se Ana não é saudável, então Paulo não está gripado.”

Comentários

Para resolver esta questão, eu utilizei a tabela da verdade (mas com certeza há outras formas mais fáceis e rápidas de resolver)…
Criei primeiro uma tabela da proposição do enunciado: ~(pˆ~q) Essa tabela resultará em V F V V
Depois, fui testando as outras proposições… E a única que deu o mesmo resultado (V F V V) foi a da letra d.
Resolvendo-se pelo caminho de tabela-verdade, demora-se 3 dias fazendo-se somente essa questão. Fazemos a negação da conjunção E e o resultado será uma disjunção OU para se achar a resposta foi feita uma equivalencia da disjunção OU que encontramos uma condicional Se ..Então conforme a letra D. Mas é necessário saber as equivalencias e negações, senão vc ficará só fazendo essa questão na prova via tabela-verdade. Abraço
Não concordo com o Gabarito. Alguém poderia me explicar porque é a letra D. Acho que seria letra C.
Resolvendo a negação dos parênteses seria
~(p ^ ~q) = ~p v q
ou seja, "Ana não é saudável ou Paulo não está gripado."

Alguém poderia me explicar o porque da letra D?
Revendo minhas anotações de Raciocínio Lógico, cheguei à seguinte forma de solucionar a questão:
Nas respostas não há a negação da proposição, mas há sua equivalente.
Sabendo que no conectivo SE ENTÃO não há negação de tudo (não se nega a primeira, mas nega a segunda), e que o conectivo SE ENTÃO é substituido por E (^) podemos fazer a seguinte relação:
SE ENTÃO = ~(p --> ~q) é igual a p ^ ~q
A questão traz ~(p ^~q)
Então inverti, acrescentando as negações e ficou assim:
~(~(p --> q)
De agora em diante não inverti os conectivos, só neguei as afirmações conforme:
~(~(se Ana é saudável então Paulo está gripado)
~(se Ana não é saudável então Paulo não está gripado)
Se Ana é saudável então Paulo está gripado.

Os especialistas por favor me desculpem e me corrijam se eu estiver errada, pois realmente não sou da área...
o operador lógico é ^ ( e ) e não o SE ENTÃO Gabarito com certeza está errado.
O correto seria letra a .
Assim como os colegas, achei a letra C como resposta, mas acho que a D tbm cabe para responder a questão, pois é uma equivalência de "se P então Q" assim como "não P ou Q". Alguém saberia mais?
Bom, corrijam-me se eu estiver errado, mas Se Ana é Saudável "E" Paulo Não está gripado, o modificador ~ (negação) faz com que Ana não seja saudável e Paulo esteja gripado, sendo assim, não haveria gabarito, tô certo?
Ou no máximo, a letra C, por colocar a disjunção!
~ (P ^ ~Q) <=> ~P v Q como não encontrei a resposta continuei ...
~P v Q <=> P -> Q
(na disjunção se negar um -> copia o outro)
A equivalencia negativa de ( P --> Q) é ( ~ P v Q) e a sua negação ~ ( ~ P v Q) seria P ^ ~ Q, todas tem o mesmo valor logico!!!
~(p ^ ~q) = ~p v q <=> p --> q (sempre devemos lembrar disto!) = “Se Ana é saudável, então Paulo está gripado.” 'D'

Bons Estudos por ai! ;D
A negação de ~(p ^ ~q) é ~ p v q.
Que seria: "Ana não é saudável ou Paulo está gripado".
Mas como não há essa alternativa, usaram uma das duas equivalentes, nesse caso a afirmação condicional: p -> q.
Concordo com a Brenda.
~(p ^ ~q) = ~p v q <=> p --> q
d) “Se Ana é saudável, então Paulo está gripado.”
d) pois possui a mesma tabela verdade que ~(p ^ ~q)
~(p ^ ~q) - v v f v
p -> q - v v f v
Nao consigo entender essa questão!!
P Q ~Q ~P (P^~Q) ~(P^~Q) ~P^~Q ~(P^~Q) ~Pv~Q P->Q

V V F F F V F V F V

V F V F V F F V V F

F V F V F V F V V V

F F V V F V V F V V
Não erro mais. :)
Gente, entendi da seguinte maneira me corrijam se eu estiver errada;
Não seria a letra C, pois a mesma pra ser correta teria que ser: Ana não é saudável ou Paulo está gripado --> ~P \/ Q

Portanto como não existe esta alternativa fica correta a letra D, Pois é uma das equivalências da condicional que na verdade a mesma que esta presentada na frase. P --> Q
Abrindo a proposição ~ (p ^ ~q) temos ~p v q, o que é equivalente a:

“Ana não é saudável ou Paulo está gripado.”

Mas essa resposta não existe nas alternativas, isso sugere que devemos encontrar uma equivalência da mesma, assim:

Sabemos que a equivalência da condicional p ➟ q = ~p v q, assim:

“Ana não é saudável ou Paulo está gripado.” = “Se Ana é saudável, então Paulo está gripado.”

Agora podemos encontrar a alternativa correta, ou seja, letra D.
Essa é a nossa velha relação da condicional muito cobrada:
p --> q <=> ~p v q ...sabendo disso resolve a questão
Outra muito cobrada é a negação da condicional:
p --> q, para negar isto vc olha para o q e nega usando a condicional:
p --> q <=> ~q --> ~p
p: “Ana é saudável.” q: “Paulo está gripado.”
~(p ^ ~q)

Primeiro faz-se a negação das proposições e conectivo, então:
~(p ^ ~ q) = (~P) V (Q)
O conectivo E vira OU e as proposições são negadas.
Como não tem nenhuma alternativa com essa resposta (~P V Q) " Ana NÃO é saudável OU Paulo está gripado" temos que achar seu EQUIVALENTE.

Daí tem que decorar equivalência mesmo para facilitar, como vi o SE nas alternativas, lembrei da equivalência do condicional SE:
P ->Q = ~ (~P V Q)
"Se Ana é saudável, então Paulo está gripado"
-------------------------------------------------------------
Obs:
O SE também tem outra equivalência que inverte a ordem a segunda proposição e se nega ambas. No caso da frase ficaria:
P->Q = ~Q -> ~P
" Se Paulo não está gripado, então Ana não é saudável"
Errei feio, mas a questão só queria saber se você sabe negar proposições compostas e suas representações equivalentes!
montando a tabela verdade
p / q / ~q / (p ∧ ~q) / ~(p∧~q)
V/ V / F/ F / V
na primeira linha já da pra resolver. afirmando que 'p' seja verdadeiro, 'q' verdadeiro, então ~q é F.
para conjunções, ambas precisam ser verdadeiras para ter valor verdadeiro. logo: (p e ~q) é F.
Daí, a negação de (p ∧ ~q) é V.
a sentença inteira verdadeira, que é como dizer "Se Ana é saudável então Paulo está gripado."
~(p ^ ~q) = ?
p ^ ~q = ~(p -> q) - (é igual à negação do condicional, conhecimento prévio).
~(p ^ ~q) = ?
~(~(p -> q)) = ?
~~ = negação de negação = afirmação!
~(~(p -> q)) = p -> q !!!!!
Resolvendo a expressão você chega fácil na frase "Ana não é saudável ou Paulo está gripado".
O problema que não tem essa frase nas alternativas, logo você tem que procurar a equivalente.
~p ou q = p -> q
Ai fica "Se Ana é saudável então Paulo está gripado".
Acho que faltou na pergunta ''''EQUIVALENTE'''''
compartilho da mesma opinião do colega Jose Santos ,a questão não deixa clara que esta querendo a equivalência
Entendi que a questão pede uma linguagem corrente, não proposição equivalente!
Demorei mas consegui entender,

para acerta essa questão você tem que entender que: ~(p ^ ~q) é igual a (~p v q)

Sabendo disso, você tem que saber também que uma das equivalências possíveis do condicional é (~p v q), logo, isso equivale a (p->q)
Questão claríssima! Segue o baile!
No primeiro momento eu errei a questão porque não reparei a negação na frente do parêntese, mas a questão é clara e a banca não precisa dizer que, quer a equivalência, isso, é de conhecimento prévio. Na dúvida vai para tabela verdade.
Questão versa sobre equivalência de conectivos:

Na proposição ~(p ^ q) = ~p v q = se p então q
EQUIVALÊCIA DA EQUIVALÊNCIA
Primeiro Nega!

Depois faz a equivalência do "ou" v.

*Nega a primeira "se então" mantem a segunda.
Para o povo que não assina:

Abrindo a proposição ~ (p ^ ~q) temos ~p v q, o que é equivalente a:

“Ana não é saudável ou Paulo está gripado.”

Mas essa resposta não existe nas alternativas, isso sugere que devemos encontrar uma equivalência da mesma, assim:

Sabemos que a equivalência da condicional p ➟ q = ~p v q, assim:

“Ana não é saudável ou Paulo está gripado.” = “Se Ana é saudável, então Paulo está gripado.”

Agora podemos encontrar a alternativa correta, ou seja, letra D.
Na verdade se formos negar a questao seria "Ana nao é saudavel OU paulo esta gripado"..
como nao tem essa resposta, deve se pressupor que trata-se de uma equivalencia.

A logica seria, se a primeira for Falsa, a segunda tem que ser verdadeira, e troca o OU por Se Entao.
ficaria como resposta a Letra D.

Se Ana nao é saudadel (1 falsa)

Entao Paulo esta gripado (2 verdadeiro)

ID

1032859

Banca

CESPE / CEBRASPE

Órgão

MTE

Ano

2013

Provas

CESPE - 2013 - MTE - Auditor Fiscal do Trabalho - Prova 1

Disciplina

Raciocínio Lógico

Assuntos

Julgue os itens subsequentes, relacionados a lógica proposicional.

A sentença “O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos” pode ser corretamente representada, como uma proposição composta, na forma P->Q, em que P e Q sejam proposições simples convenientemente escolhidas.

Alternativas

Certo

Errado

Comentários

ERRADA

Consertando o enunciado de acordo com o que foi aplicado na prova; o "P÷Q" na questão, na realidade é se P então Q:

É uma proposição é simples. Não há a presença de conectivos (por mais que exista o “e” na proposição, ele não está sendo utilizado com o intuito de unir proposições simples e portanto, não faz desta proposição uma composta.
mas " é uma consequencia" nao introduz uma condicional nao?
tipo:
"Se estudar , serei aprovado"
"ser aprovado é uma consequecia de ter estudado"

"se alguem poder ajudar, entao ficarei grato" kkkkk
o termo chave é CONSEQUÊNCIA

Montando a proposição
SE há um número excessivo de impostos incidentes sobre a folha de pagamentos ENTÃO há o crescimento do mercado informal, com empregados sem carteira asssinada.
DICA: veja os verbos. Só há um no caso. Não é só porque tem a palavra "consequência" que já é condicional. Não há uma proposição completa, ou melhor, uma ideia completa em "O crescimento do mercado informal, com empregados sem carteira assinada". E daí que seja assim?

Um exemplo de condicional seria:
Se o crescimento do mercado informal decorre de empregados sem carteira assinada, então há [como consequência] o número excessivo de impostos incidentes sobre a folha de pagamentos. (S -> P)
Ainda não entendi. Alguém poderia explicar melhor?
mais hem???? matéria do cão.
Questão ERRADA!
Tentarei esclarecer as dúvidas pertinentes dos colegas abaixo:
A questão quer saber tão somente se ela é SIMPLES ou COMPOSTA.
Ela é simples, porque não há a presença de conectivos como "...e...", "...ou...", "ou...ou...", "se...então..."(ou o se, valendo-se de que o 'então' esteja implícito na questão.) ou o "...se somente se...".
Na questão, o examinador diz que se trata de uma condicional, mas notem que não há emprego do se...então... ou apenas do "se"(com o "então" implícito) considerando assim a questão como ERRADA.
É somente isso que a questão quer saber pessoal, se há emprego de conectivo ele é composta, se não há ela é simples.
Espero ter sanado as dúvidas dos demais colaboradores abaixo.
Bons estudos a TODOS!
=)
Obrigada pela explicação, Concurseiro Focado! Agora entendi!
"O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos” Divide-se em primeira proposição: "O crescimento do mercado informal" A segunda proposição: "empregados sem carteira assinada" Terceira proposição: "é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos" Portanto seria a primeira proposição e a segunda como causa e a terceira como consequência. Logo: P^Q->R
Bom pessoal marquei errado porque não ha incidência de verbos ou conectivos
proposição simples, logo nao pode ser representada como a questão afirma. Agora o colega dizer que tem 3 proposições... Ta de sacanagem.
Seria correto de fosse ¬P->Q.
Seria correto de fosse ¬P->Q.
Errado
Não existe uma proposiçao composta no enunciado e sim uma simples, pois nao ha presença de conectivos.
Ter a palavra "consequência" na frase não significa na lógica que ela é representada pelo conectivo Se então (-->)
Não leiam o comentário do Jocelio, ele viajou...
Gabarito. Errado.
para ser uma preposição P->Q tinha que possuir o conectivo do condicional se..., então.
pra mim, a resposta é P apenas.......
Melhor não ir nessa onda de "se não tiver conectivo explícito não é condicional". Nesse mesmo ano de 2013, na prova para analista da ANS, o Cespe cobrou a seguinte questão (Q321710):

“A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino” estaria corretamente representada por P -> Q, em que P e Q fossem proposições lógicas convenientemente escolhidas."

E deu o gabarito como CERTO.

Ainda não consegui chegar em uma conclusão lógica capaz de explicar o porque da diferenciação entre os dois casos. Contudo, é um fato que se repete nas provas do Cespe que a presença da conjunção "pois" é entendida como presença de condicional (-->) enquanto a presença da palavra "consequência" não o é.

Espero ter ajudado.
Ao lermos a sentença, percebe-se que há ausência de conectivos lógicos, o que a leva ser uma proposição simples. Não se deve cometer o erro em considerar a palavra “consequência” um conectivo.
Resposta: Errado.
Façam sempre a pergunta ao verbo. Notem que só possui um sujeito , ou seja , n é uma proposição composta.
Nem Deus para entender a cabeça desses lógicos quando eles começam a se meter no português...
Só porque não tem verbo??? Não faz sentido isso... O que dizer desta frase então: "O mercado informal cresce como consequência de altos impostos serem pagos". É uma proposição composta então?

Por causa do uso do termo consequência, como nosso colega falou?
Estou em dúvida entre essas duas interpretações.
Pessoal, espero que os ajude:
Ao analisar uma assertiva como esta faço quase uma análise sintática, tentando indentificar os termos que integram a oração através do sistema S-V-C (sujeito, verbo e complemento), verifico quais conectivos presentes e por fim a semântica da coisa...
Apesar de no campo do abstrato, tenho mitigado minhas dúvidas acerca da classificação de proposições lógicas desta forma e tem dado certo!

Abraço a todos!
ERRADO - Vou aproveitar o exemplo de um amigo abaixo para explicar a diferença

1º CASO - “A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino” estaria corretamente representada por P -> Q, em que P e Q fossem proposições lógicas convenientemente escolhidas." (CERTO)
Percebe-se que nesse primeiro caso há 2 proposições, pois elas estão representadas por 2 orações (que podem ser valoradas como V ou F):
P1: A escola (sujeito) não prepara (verbo) com eficácia o jovem para a vida (complemento)
P2: o ensino profissionalizante (sujeito) não faz (verbo) parte do currículo da grande maioria dos centros de ensino (complemento)
E essas duas orações são ligadas pelo conectivo lógico "pois", que estabelece uma relação de consequência/causa (Também poderia ser utilizado "consequência", "causa", "se... então", "quando")

2º CASO (Essa questão) - A sentença “O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos” pode ser corretamente representada, como uma proposição composta, na forma P->Q, em que P e Q sejam proposições simples convenientemente escolhidas. (ERRADO)
Nesse caso há somente 1 proposição (simples), pois temos apenas 1 oração (que pode ser valorada em V ou F)
P: O crescimento do mercado informal (sujeito), com empregados sem carteira assinada (aposto explicativo), é (verbo) uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos (complemento)

Que também poderia ser reescrita:
P': O número excessivo de impostos incidentes sobre a folha de pagamentos (sujeito) é (verbo) a causa do crescimento do mercado informal, com empregados sem carteira assinada (complemento)

As orações P e P' dão a ideia de causa e consequência, porém para caracterizar proposições compostas elas deveriam ser representadas por 2 orações, o que não é o caso.

Vou postar aqui mais alguns vários exemplos para que possam fixar melhor, use sempre o conceito do nº de orações que possam ser valoradas como V ou F (lembre-se que frases no imperativo, exclamativo, interrogativo ou optativas ou abertas não podem ser valoradas, portanto não são proposições lógicas):

Q368660  (CESPE - 2014 - CADE - Nível Médio - Conhecimentos Básicos)
A sentença “Os candidatos aprovados e nomeados (sujeito) estarão subordinados (Locução verbal) ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais (complemento)” é uma proposição lógica composta. (ERRADA)

Q355836  (CESPE - 2013 - STF - Técnico Judiciário - Área Administrativa)
A sentença “A indicação de juízes para o STF deve ser (imperativo) consequência de um currículo que demonstre excelência e grande experiência na magistratura” pode ser corretamente representada na forma P→Q, em que P e Q sejam proposições simples convenientemente escolhidas. (ERRADA - Está errada por ser imperativo "deve ser")

Q344285 (CESPE - 2013 - MTE - Auditor Fiscal do Trabalho - Prova 1)
A sentença “Quem é o maior defensor de um Estado não intervencionista, que permite que as leis de mercado sejam as únicas leis reguladoras da economia na sociedade: o presidente do Banco Central ou o ministro da Fazenda? (Frase Interrogativa)" é uma proposição composta que pode ser corretamente representada na forma (P∨Q)∧R, em que P, Q e R são proposições simples convenientemente escolhidas. (ERRADA - Frase interrogativa)

Q321711  (CESPE - 2013 - ANS - Analista Administrativo)
A expressão “Como não se indignar, assistindo todos os dias a atos de violência fortuitos estampados em todos os meios de comunicação do Brasil e do mundo?” é uma proposição lógica que pode ser representada por P -> Q , em que P e Q são proposições lógicas convenientemente escolhidas. (ERRADA - Frase interrogativa)

Q313207 (CESPE - 2013 - IBAMA - Analista Ambiental - Tema 2)
A proposição “Fiscalizar os poderes constituídos (Sujeito) é (verbo) um dos pilares da democracia (complemento) e garantir a liberdade de expressão (sujeito), [é] (Verbo) outro pilar da democracia (complemento)” pode ser corretamente representada por P∧Q. (CERTA)
Pessoal, observem o comentario de nossa colega dani logo abaixo, otimo comentario e esclarece as duvidas de uma maneira ampla. parabens.....
Essa questão considero uma espécie de pegadinha. Segundo o comentário do prefessor (disponibilizado na questão), não devemos cair no erro de considerar a palavra "consequencia" um conectivo.
Outras "pegadinhas" famosas:
Utilizar sujeito composto em proposição simples:
"Maças e Laranjas são doces" - É uma proposição simples

Sentença paradoxal:
"Esta frase é uma mentira" - Não é proposição
Eu considero como sendo sim uma proposição composta, na verdade a banca cobrou o assunto "condição" e explico:
Explicação: no conectivo "se então" o antecedente é condição SUFICIENTE, o consequente é condição NECESSÁRIA. Ou seja: P= "O crescimento do mercado informal, com empregados sem carteira assinada" Q=, "é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos”
Percebe-se, ao ler a frase, que P não seria condição SUFICIENTE para Q (P-->Q), mas sim Q seria suficiente para P (Q-->P), pois é o "número excessivo de impostos incidentes sobre a folha de pagamentos" (Q) que fazem com que haja " O crescimento do mercado informal [...]" estão vendo como faz mais sentido?
Portanto a correta representação, como uma proposição composta, seria na forma Q->P.
Excelente explicação da Dani. Uma verdadeira aula de Raciocínio Lógico.
Eu pensei exatamente como o Marcones!
Excelente comentário da Dani, além de ser uma aula de Raciocínio Lógico, é também de Análise Sintática! :)
Lendo o comentário da Dani, me surgiu uma dúvida.
Não é vedado o uso da vírgula entre sujeito e verbo ?
Não estou afirmando que estou certo, isso é só uma dúvida minha.
Lucas, essa é a regra geral. No entanto, quando há expressão intercalada (oração, aposto etc), esta deve vir separada por vírgulas.
Excelente explicação de Dani Concursanda!! Obrigada!!
Proposição simples, demonstra uma única ideia, pode ser verdadeira ou falsa.
“O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos”

O que devemos analisar para a CESPE:

Número de verbos: 1 verbo, 1 oração, proposição simples

Cuidado! Se você for analisando logo de cara, tentando "fazer uma condicional", vai coneguir!!

Melhor caminho é sempre ver se é uma proposição composta ou não antes de ver o tipo de proposição!
“O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de
APOSTO EXPLICATIVO VL
impostos incidentes sobre a folha de pagamentos”
=================================================================================
P: “O crescimento do mercado informal é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos”
Proposição simples. Podemos perceber que segue uma só linha de pensamento, uma só ideia.
Errada
É uma proposição simples, onde não se pode extrair mais de uma com sentido completo. Não tem nem como ver qual é o antecedente(condição suficiente) ou qual é o consequente(condição necessária).
Quando for questão assim, procura os verbos primeiro

1 verbo ''ser''

1 oração

Preposição simples
Não há lógica nisso. se a banca bem quisesse, poderia colocar o gabarito como "certo" e justificá-lo. Há questões parecidas com essa que a banca coloca como certo, e aparecem justificativas. Muito relativo.
ATENÇÃO COM A PALAVRA CONSEQUÊNCIA!

Quando a palavra consequência aparecer na frase observe se há uma relação de causa/efeito e se houver será proposição composta. Além disso, se há entre a palavra "consequência" dois verbos (de preferência no infinitivo) será uma proposição composta, se não houver, é simples.

Ex.: Passar (v. no infinitivo) é uma consequência de estudar (v. no infinitivo) = prop. composta

Ex.: A educação é (apenas um verbo) uma consequência de um país sério = prop. simples

A estabilidade econômica é (um verbo) dever do Estado e consequência (não há verbo após a palavra consequência) do controle rígido da inflação = proposição SIMPLES.
Para auditor todas são obvias,brincadeira como para tecnicos tudo e dificil.
Muitas explicações incorretas e imprecisas...

Experimente o mais simples: procure pelos conectotivos clássicos: E, OU, SE, ENTÃO, SOMENTE

Não encontrou? Pode assinalar como PROPOSIÇÃO SIMPLES sem medo de ser feliz !
ERRADO

ESSA MALDITA QUESTÃO CAIU NA PROVA DA ABIN 2018

ELA INDUZ A GENTE ERRAR QUANDO FALA EM "consequência" QUERENDO VALORAR COMO "SE ENTÃO"

Ano: 2018 Banca: CESPE Órgão: ABIN Prova: Oficial Técnico de Inteligência - Conhecimentos Gerais

Julgue o item a seguir, a respeito de lógica proposicional.

A proposição “A vigilância dos cidadãos exercida pelo Estado é consequência da radicalização da sociedade civil em suas posições políticas.” pode ser corretamente representada pela expressão lógica P→Q, em que P e Q são proposições simples escolhidas adequadamente.

GABARITO ERRADO
Tem o conectivo ? Não .Então, Pau no burro.
O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos

VERBO ANTE...é uma consequência do. VERBO DEPOIS BIZU: JHONI FOCUS ! SÓ VAI SER UMA CONDICIONAL " SE NÃO " SE ANTES DA PARTE EM VERMELHO TIVER VERBO E DEPOIS DA PARTE VERMELHA TIVER VERBO. Lembrando que o "é " em vermelho não conta.

EX: ESTUDAR É UMA CONSEQUENCIA DE PASSAR . VERBO ANTES E DEPOIS.
Já sabemos que o posicionamento do CESPE é que se temos apenas uma oração principal, estamos diante de uma oração simples. “O crescimento do mercado informal, com empregados sem carteira assinada, é uma consequência do número excessivo de impostos incidentes sobre a folha de pagamentos”.
Podemos ver que não é possível reduzir a frase, também não temos nenhum conectivo, portanto, esta é uma proposição simples.
Desta forma, não podemos representa-la como uma proposição composta P Q.
Importante: Quando a palavra consequência aparecer na frase, devemos observar se há uma relação de causa/efeito e se houver será proposição composta. Além disso, se há entre a palavra "consequência" dois verbos (de preferência no infinitivo) será uma proposição composta, se não houver, é simples.
Gab E Proposição Simples
Na condicional ( →):
- O antecedente é condição suficiente para o consequente e;
- O consequente é condição necessária para o antecedente.

"é consequência de" -> para ser condicional tem que ter "verbo antes e depois" -> se ñ tiver um dos dois verbos: proposição "simples".

VEJA-SE:

Q555366 A sentença “A aprovação em um concurso é consequência de um planejamento adequado de estudos" pode ser simbolicamente representada pela expressão lógica P → Q, em que P e Q são proposições adequadamente escolhidas. Gabarito: Errado
SEGUI O MESMO RACIOCINEO

ID

1032862

Banca

CESPE / CEBRASPE

Órgão

MTE

Ano

2013

Provas

CESPE - 2013 - MTE - Auditor Fiscal do Trabalho - Prova 1

Disciplina

Raciocínio Lógico

Assuntos

Julgue os itens subsequentes, relacionados a lógica proposicional.

A sentença “Quem é o maior defensor de um Estado não intervencionista, que permite que as leis de mercado sejam as únicas leis reguladoras da economia na sociedade: o presidente do Banco Central ou o ministro da Fazenda?” é uma proposição composta que pode ser corretamente representada na forma (P∨Q)∧R, em que P, Q e R são proposições simples convenientemente escolhidas.

Alternativas

Certo

Errado

Comentários

Acredito que o erro da questão é que uma interrogação, ou seja, uma pergunta não pode ser uma proposição composta.

por favor, se o erro não for esse me avise.

espero ter ajudado!!
ERRADO

Vale transcrever o enunciado correto:
" A sentença “Quem é o maior defensor de um Estado não intervencionista, que permite que as leis de mercado sejam as únicas leis reguladoras da economia na sociedade: o presidente do Banco Central ou o ministro da Fazenda?” é uma proposição composta que pode ser corretamente representada na forma (PVQ)∧R, em que P, Q e R são proposições simples convenientemente escolhidas."

Resposta de acordo com o AprovaConcursos:
A sentença não é uma proposição pois interrogações (perguntas) não podem ser classificadas como Verdadeiras ou Falsas. Sendo assim, ela não é proposição e muito menos proposição composta.
NÃO HÁ PROPOSIÇÃO NAS FRASES:

Interrogativas (?)
Exclamativas (!)
Imperativas
Expressão algebricas - não se pode afirmar o que é verdade
sentenças sem verbos

fonte: Alfacon
Exemplos:
Pare de fazer o dever, João! (imperativa)
João, já fez o dever? (interrogativa)
João, que susto! (exclamativa)

X é um número par. (qual o valor de x?)
Ele é advogado. (sujeito é "indefinido")
Belo momento de alegria (frase nominal).

Em nenhum dos casos acima, é possível atribuir V ou F. Não são proposições.
Na Logica sequencia denomina-se PROPOSIÇÃO uma frase que pode ser julgada com V ou F

E FRASES EXCLAMATIVAS não podem ser valoradas, portanto NÃO SÃO PREPOSIÇÕES, e são chamdas de SENTENÇA ABERTA
Tradicional pega ratão.. kkk a banca coloca uma questão enorme pra tirar o foco da frase interrogativa.
Cheguei ate a interrogativa e já marco como ERRADA!

Nas interrogativas não ha valor logico.
A primeira coisa que vejo em uma pergunta dessas é se a declaração possui ? ! , nesse caso abro o sorriso sabendo que não é proposição
Gabarito. Errado.
frases interrogativas não possuem valor lógico .
Questão errada.
Expressões dessa forma são denominadas sentenças
abertas, ou funções proposicionais, pois não tem sentido completo.
INTERROGATIVAS,
EXCLAMATIVAS,
IMPERATIVAS.

Fonte: professor BRUNNO LIMA, VOU PASSAR
Analisando a questão,
É sabido que uma proposição é uma sentença declarativa, seja ela expressa de forma afirmativa ou negativa, na qual podemos atribuir um valor lógico “V” (verdadeiro) ou “F” (falso). A sentença dada no enunciado é interrogativa, sendo assim a mesma nem chega a ser uma proposição.

RESPOSTA: ERRADO
Apareceu interrogação já não é proposição!! Não precisa olhar mais nada!!
Gabarito: errado

Proposição é toda sentença declarativa fechada.
Não são proposições:
Ex:
Bom dia! ( sentenças exclamativas)
Que horas são? (sentenças interrogativas)
Vá para o quarto (sentenças imperativas)
X é a capital da Alemanha ( sentenças abertas)
Errado
Não são proposições:
- perguntas (?)
- exclamações (!)
- ordens (.)
- sentenças abertas
ERRADO
Quem disse que PERGUNTA pode ser proposição?
Gabarito: Errado

Não são proposições:
Exemplos:
Brasília é a capital federal ? (Frase Interrogativa)
Estudem! (Frase Exclamativa)
Vá lavar o carro. (Frase Imperativa)
Alguém é alto. (Sentença Aberta, afinal qm é alto ?)
pergunta não é considerada preposição
Proposições são frases declarativas, porquanto as interrogativas não são consideradas proposições.
Frases exclamativas, interrogativas e optativas(fulano é bonito, ciclano é forte) não são proposições.
Quando vi a interrogação fui logo para resposta. ERRADO.
O meu sentimento é que que as provas de ensino superior são mais tranquilas do que às de ensino médio.
Frases interrogativas não são consideradas preposições!
Fé em Deus!
Errada
Frases interrogativas não são proposições!

Quem é o maior defensor de um Estado não intervencionista, que permite que as leis de mercado sejam as únicas leis reguladoras da economia na sociedade: o presidente do Banco Central ou o ministro da Fazenda?
Cuidado ! Galera,

Às vezes, a oração pode ter o sinal de INTERROGAÇÃO e ser ,perfeitamente, uma PROPOSIÇÃO. É necessário analisar cada questão com minuciosidade.

Ex.: Quem publicou a Teoria da Relatividade ? Foi Albert Einstein. (É PROPOSIÇÃO)

As provas do Cespe são interdisciplinares.Se não dominarmos o português em RLM, beiramos a tragédia.
Frases INTERROGATIVAS

IMPERATIVAS

EXCLAMATIVA

com SENTENÇA ABERTA

NÃO SÃO PROPOSIÇÕES
mesmo que fosse uma proposição, não corresponderia a formula, pois seria mais ou menos assim:

P: O maior defensor de um estado NÃO é intervencionista.

Q: As leis de mercado são as únicas leis reguladoras da economia na sociedade.

¬p então q
frase interrogativa..
A sentença dada no enunciado é interrogativa, sendo assim a mesma nem chega a ser uma proposição.

GABARITO ERRADO
Essa é para pegar distraido!
Nem proposição é.
PRESTA ATENÇAO NO USO DA INTERROGAÇAO
tem uma interrgoação no final. logo não é proposição.
Olá pessoal,

Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/T-gOdcyRA4U

Professor Ivan Chagas
www.gurudamatematica.com.br
Perguntas nem ordens são proposições!
Fazenda? NÃO PRECISA NEM CONTINUAR A LEITURA.

GABARITO = ERRADO

PM/SC

DEUS PERMITIRÁ
ERRADO
vide conceito que o próprio cespe/cebraspe colocou em prova.
Q418951 - No conjunto de todas as frases, as proposições encontram-se entre aquelas classificadas como declarativas e verbais, ou seja, entende-se como proposição todo conjunto de palavras ou símbolos que exprimam um pensamento de sentido completo, para o qual seja possível atribuir, como valor lógico, ou a verdade ou a falsidade. Assim, as proposições transmitem pensamentos, isto é, afirmam fatos ou exprimem juízos que se formam a respeito de determinados entes. Com base nessas informações, julgue se o item a seguir é proposição.

Que excelente local de trabalho!

Gab. ERRADO
NÃO SÃO PROPOSIÇÕES.

FRASES IMPERATIVAS (Que passam ideia de ordem, conselho).
FRASES INTERROGATIVAS. (?)
FRASES EXCLAMATIVAS (!)
SENTENÇAS ABERTAS (x+y < 5)
PARADOXO (Frases que se contradizem ex: Estou mentindo agora)

Normalmente Frases que se utilizam de pronomes (ele e ela) também não são proposições.

QUESTÃO: ERRADA.
frase interrogativa não é proposição :)
Gabarito Errado.
Frases interrogativas não são proposições.
As frases interrogativas não são proposições, pois não podem ser valoradas como “V” ou “F”.
A principal característica de uma proposição é a possibilidade de valorá-la como verdadeira (V)ou falsa (F)
São proposições:
- Verbo (mesmo se implícito).
- Sentido completo.
- Possibilidade de julgar se é verdadeiro ou falso.
Não são proposições:
- Frases exclamativas: “Meu Deus!”
- Frases interrogativas: “Você me ama?”
- Frases imperativas: “Não estude para passar, mas até passar!”
- Frases sem verbo: “O mundo dos concursos públicos.”
- Frases abertas: “x + 1 = 7” ;
- Frases paradoxais: “Só sei que nada sei.”

ID

1045009

Banca

IBFC

Órgão

EBSERH

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Se o valor lógico de uma proposição p é verdadeiro e o valor lógico de uma proposição q é falso então o valor lógico da proposição composta [(p → q) v ~p ] ^ ~q é:

Alternativas

Falso e verdadeiro

Verdadeiro

Falso

Inconclusivo

Comentários

Se o valor lógico de uma proposição p é verdadeiro e o valor lógico de uma proposição q é falso então o valor lógico da proposição composta
[(p → q) v ~p ] ^ ~q é:

[(p → q) v ~p ] ^ ~q
   V        F
         F    v     F
                F         ^    V
                         F

Letra C

Força e bons estudos ;D
A diagramação aqui no site ficou errada e por isso aqui está a questão:
Letra C
Bons estudos a todos nós! Sempre!
Se P for verdadeiro, ~P será falso
Ou seja, ~P é o contrário de P

Se Q for verdadeiro, ~Q será falso
Ou seja, ~Q é o contrário de Q

TABELA RESUMO DOS CONECTIVOS:

BONS ESTUDOS A TODOS NÓS! SEMPRE!
Para facilitar a vida dos colegas, não precisa decorar tabela ou fórmula alguma.
Essa questão é relacionada a condicional Se... Então.
Podemos resolver analisando por parte da seguinte forma:
P é Verdadeiro
Q é Falso
o valor lógico ( o resultado) será sempre Falso.

O bizu para questões de Se... Então é:
Só será Falso de V para F.
Levem apenas essa informação de V para F é F.
O resto será sempre verdadeiro.
Esse bizu que deixo é realmente apenas para acertar a questão da prova.
Boa Sorte!!!
olha como veio pra mim....[(p→ q) v ~p ] ^ ~q é: ta certo isso pra quem ta qrendo aprender....
O único jeito de se obter valor lógico F em uma condicional (--->) é se a proposição 'p' for - V - e a proposição 'q' for - F-.
como na questão tinhamos:
[( V --> F) ou F] e V
= [F ou F] e V
F ^ V = proposição Falsa.
Montou a tabela com os valores de P e Q.....Resolva na regra os valores logicos....1 conjunção,2 dijunção....e observando parenteses e etc....vc vai observar que o resultado será com certeza falso.....sem misterios...
De acordo com o enunciado, p é verdade e q é falso, assim, fazendo por partes:

P → q = F

Fv ~p = F

F^~p = F

Logo, [(p → q) v^~p] ^~q = F.

Letra C.
P=V; Q=F, se você prestar atenção cada conjunção(e, ou, se...então e se...somente ...se, OU..OU), tem um correlação com com quadro verdades, sabendo dessa correlação, você saberá exatamente como resolver apenas dessa forma abaixo.
exemplo: No caso, o "se..então" só será negativa caso a primeira proposição seja verdadeira e a segunda falsa.
[(p->q) v (~p)] ^ ~q
[(F) v (F)] ^ (V)
[F] ^ (V)
= F
Obrigado Djanilson Lopes, dúvida solucionada ,,, muito grato ....flw
Boa tarde , pessoal sou novo por a que , semana passa fiz uma prova pra um concurso e a questão caiu em minha prova,
Se o valor lógico de uma proposição é falso e o valor
lógico de outra proposição é verdade, então o valor
lógico do condicional entre eles, nessa ordem, é:
a resposta que marquei foi, falso ou verdadeiro, no gabarito a resposta certa foi verdadeiro, mas vi que cabe recurso, pois a que vi que pode ser falso tmb, se pode ser as duas coisas a minha resposta pode ser entendida como certa, preciso de ajuda pro recurso. meu email e weuquesxavier@hotmail.com
Eu resolvi assim galera
[p(v) =>q(f)=F] ^ ~q(v) = F
na conjunção os precisam ser V para ser V, logo é falso.
P = V
Q = F
~P = F
~Q = V

1 - [(P --- > Q)] v ~P ] ^ ~Q
2 - [(V ---> F)] V F] ^ V
3 - [ F V F] ^ V
4 - F ^ V = F
Primeiro resolve-se o que encontra-se dentro do parênteses, colchetes ...
obedecendo o seguinte;
primeiro negações
depois conjunções
terceiro disjunções
quarto condicionais ..
1º) p -> q (V -> F) => F
2º) [F v ~p] .: F v F => F
3°) F^~q .: F ^ V => F
Tenho que "p" é verdadeiro e "q" é falso. Resolve o que está dentro dos parênteses e colchetes primeiro.
[(p->q) v ~p ] ^ ~q
p -> q - Temos V+F, logo a proposição é falsa, pois a proposição "se então" só será falsa quando eu tiver V+F.
~p - é a negação de p, se p é verdadeiro ~p é falso.
Logo ficamos com duas falsas no colchete, com o conectivo "v" (ou). Este conectivo só será verdadeiro se pelo menos uma das proposições for verdadeira. Como neste caso temos duas falsas a proposição entre colchetes é falsa.
Por último temos a proposição entre colchetes (que já sabemos que é F) e a negação de q, ~q. Como q é falsa, sua negação verdadeira. Porém aqui temos o conectivo "^" (e), que estabelece que a proposição só será verdadeira se tivermos duas proposições verdadeiras.
Dessa forma, a proposição é falsa, pois tenho F ^ V.
Demorei, mas entendi...Wuuf....
Valeu galera, pelas dicas!
p q p→q ~p [(p→q)v~p]
v v v f v
"v" "f" f f "f"
f v v v v
f f v v v

QUESTAO FALA QUE LETRA P É V E QUE A LETRA Q É F
Portando, só achar na tabela o resultado. C

:)
Resolvendo a questão:
Temos que P é verdadeiro e Q é falso então:
[(P->Q) V~P]^~Q (resolvendo por partes) :
(P->Q): Temos que P é verdadeiro e Q é falso: V->F, sabemos que em uma condicional (se...então) só é falsa quando o resultado é falso então V->F é Falso (P->Q)= F
Agora pegamos o nosso resultado e a segunda parte da afirmativa V~P] temos:
FV~P (Sabemos que P é verdadeiro, então ~P é falso)= F V F. Sabemos que em uma disjunção (ou) só é falsa se a condição e o resultado forem falso (FF). Então F V F = F
Agora pegamos o nosso segundo resultado e a terceira parte da afirmativa ^~Q temos:
F^~Q (Também sabemos que uma conjunção (e) só será verdadeira se a condição e o resultado forem verdadeiros (VV). Então F^V = F Logo essa afirmativa é falsa.
Então essa afirmativa é falsa! Alternativa C
Gabarito C

P = V , Q= F

[(p → q) v ~p ] ^ ~q

[(V -> F) v F] ^ V

[F v F ] ^ V

F ^ V

F

"Retroceder Nunca Render-se Jamais !"
Força e Fé !
Fortuna Audaces Sequitur !
Na condicional a unica maneira de ser falso: V F F(VERA FISCHER FALSA)
Se o valor lógico de uma proposição p é verdadeiro e o valor lógico de uma proposição q é falso então o valor lógico da proposição composta.

---> (CONDICIONAL) SE, ENTÃO: Não precisa resolver. Questão para perder tempo!

P=V

Q=F

V ---> F = F
Resolução de questão similar https://www.youtube.com/watch?v=JV5VQ0nn4n0
Gabarito: C

[(P -> Q) v (~P)] ^(~Q)]

[(V -> F) v F ] ^ V ]

[ F v F ] ^ V

F ^ V

F
c-

p -> v
q -> f

v-f --->f

(f)\/f --->f

f^v ---> f
Vamos com tudo.
Tudo v da v
Tudo f da f
Iguais dá f diferentes dá v
Vera fícher falsa
Iguais da v diferentes da f

ID

1060459

Banca

CESPE / CEBRASPE

Órgão

PC-DF

Ano

2013

Provas

CESPE - 2013 - PC-DF - Agente de Polícia

Disciplina

Raciocínio Lógico

Assuntos

Considerando que P e Q representem proposições conhecidas e que V e F representem, respectivamente, os valores verdadeiro e falso, julgue o próximo item.

As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.

Alternativas

Certo

Errado

Comentários

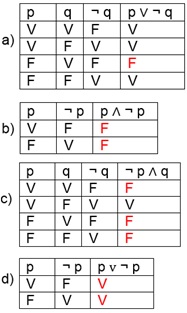
Tabela Verdade
P Q ¬Q P->(¬Q)
V V F F
V F V V
F V F V
F F V V

Portanto gabarito errado, pois P sendo F, há uma possibilidade para que a expressão Q seja F.
A questão fala em simultaneidade.
Freddie, a questão fala em SE, E SOMENTE SE, P for Falso, mas há uma possibilidade em que ele sendo verdadeiro a proposição será verdadeira.
Não consegui entender. Mesmo. Alguém pode me ajudar?
Faz-se a tabela verdade, lembrando que para o conector e ( ^ ) será V qdo todos forem V. Se então (-->) será F quando for V F. (Dica se Vera Fisher então - Falsa = V F - F). E o conectico se e somente se sera V quando todos forem V ou todos forem F.
Montando a tabela Verdade P Q
P     Q    ¬Q      P -> (¬Q) SE FOR V F = F)    Q ^ P (SE FOR V V = V)
V     V      F          F (VERA FISHER)      V
V     F      V          V                                              F
F     V      F          V                                              F
F     F      V          V                                              F

Ele pergunta se são V, se e somente se P for F. Só pode ser V se P e Q for V.
O que sabemos logo de cara que para o conectivo e só é V se forem todos V.
Caros, a questão está certa, uma vez que as proposições Q e P -> ¬Q serão simultaneamente verdadeiras (forem verdadeiras ao mesmo tempo), somente quando P for Falsa. Basta olhar a tabela verdade.

P Q ¬Q P -> ¬Q

V V F F

V F V V

F V F V

F F V V

Danilo Capistrano,

Onde está a possibilidade onde P é V e, ao mesmo tempo, Q e P→(￢Q) são V????

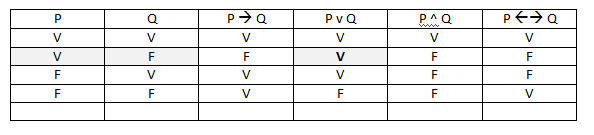
O único erro que consegui identificar, depois de muito sufoco foi o fato de que mesmo com Q=V, P→(￢Q)=V e P=F, o "se e somente se" é falso, conforme a tabela verdade a seguir:

P	Q	¬Q	P -> ¬Q	Q^(P->¬Q)	(Q^{P->¬Q}) <->P
V	V	F	F	F	F
V	F	V	V	F	F
F	V	F	V	V	F
F	F	V	V	F	V

Danilo, também cheguei à mesma conclusão que o colega Matheus Eleutério. Para a proposição P->(¬Q) realmente existe a possibilidade de valor Verdadeiro quando P for Verdadeiro, conforme sua análise acima. O problema, é que a questão não pede somente a análise dessa proposição (P->(¬Q)). A questão afirma que só existe valor Verdadeiro, simultaneamente (ao mesmo tempo) para as proposições Q e P → (￢ Q) (isso mesmo, são duas proposições e não apenas P → (￢ Q)), se e somente se, P for Falso. O que está corretíssimo (conforme podemos verificar na própria tabela verdade que você, corretamente, construiu).
Portanto o item é CORRETO!
E o gabarito está INcorreto!
Pessoal, realmente ao montar meu comentário não fui feliz em explicar detalhadamente a questão.
copiando a tabela do colega Matheus
P
Q
¬Q
P -> ¬Q
Q^(P->¬Q)
(Q^{P->¬Q}) <->P
V
V
F
F
F
F
V
F
V
V
F
F
F
V
F
V
V
F
F
F
V
V
F
V

Pois uma opção que P sendo F já abre margem para a questão estar incorreta, pois há uma opção em que ele sendo F a proposição Q é F.

A questão deixa bem claro SIMULTANEAMENTE.

Gabarito definitivo da cespe: E
Essa questão não coube recurso.
Para quem continuar com dúvidas podem acessar este link do youtube com a explicação.

http://www.youtube.com/watch?v=OUD6GH1nk4I
a partir do 35:17

Espero que tenham compreendido.

abraços,
forças nos estudos.
Q(f) e P(f) = F --> (~Qv)= V...Questão errada
Pensei da seguinte forma: Q e P → (￢ Q) , se Q for falso, a proposição ficaria F e P → (￢ F) = F e P → V . Como na condicional qualquer coisa implicando em verdade será sempre verdade, o valor de P não importa nesse caso.
Estou correto?
não há como Q e P → (￢ Q) serem simultaneamente VERDADEIRAS, pois para Q e P ser VERDADE os dois precisam ser VERDADEIROS e se ￢ Q é a NEGAÇÃO de Q (v) não há como Q e P → (￢ Q) ser simultaneamente VERDADEIROS! Q(V) e P(v) → (￢ Q)(f)!
Questão Certa... só não sei sinceramente se foi anulada. vejam o comentario do aprova concursos: http://www.aprovaconcursos.com.br/noticias/2013/11/12/gabarito-comentado-concurso-pc-df-raciocinio-logico/

48 As proposições Q e P são, simultaneamente, V se, e somente se, P for F.
Q verdadeira
P à ~Q (verdadeira)
Então teremos P à Falso
Para que esta sentença seja verdadeira, P tem que ser Falsa.
CERTO
Gabarito oficial: ERRADO
Acredito que seja mais interpretação que qualquer coisa, nas proposições que o exercício dá se tem Q e ~Q, ele fala de os dois serem simultaneamente verdadeiros,o que não é possível pois se um nega o valor do outro é impossível os dois terem mesmo valor.
Q pode ser V ou F. Se Q for V, P deverá ser F.
Mas, se Q for F, P poderá ser F ou V. Porque ~Q será V e não restringirá o P.
P1 --> P2 = P1 verdadeiro --> P2 falso = FALSO
Q ^ P --> ( ¬ Q) = FALSO
P1 falso --> P2 falso = VERDADEIRO (se então)
P1 falso <--> P2 falso = VERDADEIRO (se, e somente se)
Correta, simultaneamente verdadeiras se, e somente se, P for F
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.
São duas proposições: Uma simples e uma composta.
Para Q=V ; P → (￢ Q)=V temos:
Q=V; F → F = V
Q=F; V → V= V

Agora: Se Q=V e P=V então (￢ Q) será F.
E Vera Fischer na condicional é F.
A questão esta errada porque não depende apenas do P ser V, mas tbm porque depende do Q ser F.
Gabarito Errrado
Questão mal formulada, de difícil interpretação. Vamos a ela:
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.
Primeiro ponto: Esse "e" não é conectivo, é uma preprosição que está dando ideia de adição das informações, ou seja, a questão afirma que se P for F, ambas as proposições ( Q e P → (￢ Q) ) terão o valor lógico V.
Ora, analisando a proposição: P → (￢ Q), se P for F, logo a proposição necessariamente será V, pois o conectivo → só é F quando tiver valores lógicos respectivos V → F. Analisando a proposição simples Q, concluimos que se P for F, de nada irá influenciar nesta proprosição. Logo, não podemos afirmar que ela será Verdade. Portanto gabarito ERRADO.

BONS ESTUDOS
ESSE "e" É CONECTIVO SIM E FOI USADO COMO TAL NA QUESTÃO.
OS conectivos são:
"e"
"ou"
"se.. então"
"ou...ou.."
"se e somente se"
Essa é uma questão que cobra o conhecimento dos conectivos "E" e SE...ENTÃO e não do SE E SOMENTE SE como alguns interpretaram erroneamente (induzidos pela banca). Nessa questão a banca usou o termo "se e somente se", com o valor sintático de "tão somente" e não como conectivo.
Nós podemos sim ter questões ligadas pelo conectivo "E", ou pelo conectivo "OU", e seguidas do conectivo "SE ENTÃO" e vice-versa.
O que, com certeza, não existe em RL, é essa idéia de preposição com valor de adição.
eis um exemplo:
04. (MPU 2004 ESAF) Quando não vejo Carlos, não passeio ou fico deprimida. Quando chove, não passeio e fico deprimida. Quando não faz calor e passeio, não vejo Carlos. Quando não chove e estou deprimida, não passeio. Hoje, passeio. Portanto, hoje
a) vejo Carlos, e não estou deprimida, e chove, e faz calor. b) não vejo Carlos, e estou deprimida, e chove, e faz calor.
c) vejo Carlos, e não estou deprimida, e não chove, e faz calor.
d) não vejo Carlos, e estou deprimida, e não chove, e não faz calor. e) vejo Carlos, e estou deprimida, e não chove, e faz calor.
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.
---------------------------------------------------------------------------------------------
Aqui temos duas senteças quaisquer! Essas sentenças representam frases quaisquer como:
Q = Maria estuda.
P = Paulo trabalha.
~Q = Maria não estuda. (A NEGAÇÃO DE Q).
Além das sentenças isoladas, temos os agrupamentos resultantes do uso dos conectivos. A resposta deve ser dada a respeito da sentença composta resultante após o uso dos conectivos “E” e “SE ENTÃO”.
Sentenças ligadas por “e” somente serão verdadeiras se ambas forem verdadeiras. Logo, uma delas sendo falsa, o valor lógico da sua “soma” será falso.
Aqui a questão já estaria respondida como ERRADA, já que uma vez “P”assumindo F, não teremos, na soma de Q+P, o valor lógico verdadeiro.
***Sentenças ligadas por “e” somente serão verdadeiras se ambas forem verdadeiras***
Assim, analisando apenas as proposições ligadas pelo conectivo “e”, já não há mais possibilidade de serem ,ambas as sentenças, simultaneamente verdadeiras.
Q P QeP ~Q PeQ --> ~Q
V V V F F
V F F F V
F V F V V
F F F V V
PARA A CONDICIONAL sim, quando P =“F”,independentementedo valor da segunda parte (~q), o valor final será VERDADEIRO.
Mas....
Olhe para a penúltima linha, veja que quando P assume valor lógico V, o valor lógico da condicional é VERDADEIRO. LOGO: *não é verdade que tão somente se P=F teremos a condicional VERDADEIRA, também teremos a condicional VERDADEIRA quando P=V.
São dois os erros.
Pessoal, como a questão pede se e somente se, temos que analisar a "ida" e a "volta":
Se Q = V e P-> (~Q) = V, então P=F. Porém, P = F não implica que as proposições Q e P->(~Q) serão verdadeiras. Então a afirmação está errada.
Simples , tabela verdade básica:
SE VC CONSIDERAR (~Q ) = V como pede a questão,
logo concluímos que Q = F, dando margem
a dois possíveis resultados para P.
Assim P pode ser V OU F que (~Q)=V.
errada a questao.
Nem é preciso montar a tabela verdade! Se P for falsa, o Q pode ser qualquer valor lógico que a a proposição P->(¬Q) será verdadeira. Assim, NÃO necessariamente Q será verdadeira se o P for falsa. Entendeu?
Questão mal formulada! Errei por não levar em conta que a primeira afirmação independe da segunda.
GABARITO = ERRADO
"P" = Verdadeiro
"Q" = Falso
P-> ( ˜ Q)
V -> V
Boa noite pessoal,
Desculpe Danilo, mas essa opção não existe, pois se P for F fará o antecedente sempre ser F e pela tabela mostrada por você mesmo, se o antecedente (P) for F, então o P->(¬Q) será sempre verdadeiro. Olhe as duas últimas linhas da sua tabela.
Acontece que a questão possui uma pegadinha no texto, pois na linha de comando há duas proposições totalmente independentes entre si e que o CESPE interligou com um "e" texto e não um "e (^)" conectivo, pois na segunda proposição não utilizou o "se, então", mas sim os conectivos.
Sendo assim, para a primeira proposição simples, apenas Q, independe o valor de P para que esta seja F ou V.

Espero ter ajudado....
Foco é tudo....
Obrigada Danilo Capistrano pelo vídeo, só fui entender quando assisti ele, recomendo para os colegas que estão com dúvidas também...
Para resolver essa questão, primeiramente o candidato deverá ter cuidado ao ler o enunciado, quando ele diz “As proposições Q e P → (￢ Q)” o conectivo e não é um conectivo lógico, até porque ele se refere no plural.

De acordo com os dados do enunciado:

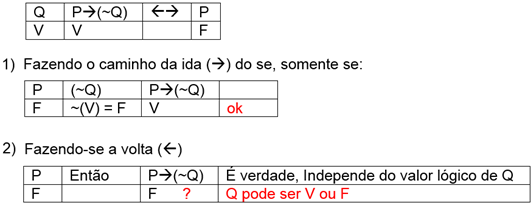
Logo, para que a condição do se, e somente se seja satisfeita, a ida e a volta devem ser válidas, mas como se vê, fazendo a prova da volta, Q pode ser V ou F que não vai alterar a validade da estrutura Pà(~Q).

Resposta é: Errado.
Se e somente se só será verdade se P=Q, logo, se ele fala em F jamais será V ou vice-versa.
Acho que o Diego Wisintainer, acertou em seu comentário.
ERRADO
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.
P ser uma proposição falsa não garante que Q será verdadeira. Pois na condicional [P → (￢ Q)], a verdade do antecedente garante a verdade do consequente para que a proposição seja verdadeira, mas a inveracidade do antecedente (Falsa) não nos garante nada, podendo o consequente ser Verdadeiro ou Falso.

[Q e P → (￢ Q) são Verdadeiras] <-> P for Falsa.

Se "P for falsa", o segundo termo da bicondicional é VERDADEIRO.
[Q e P → (￢ Q) são Verdadeiras] <-> V

Logo para a proposição ser verdadeira, o primeiro termo também tem que ser VERDADEIRO [Q e P → (￢ Q) são Verdadeiras] :
P → (￢ Q)
F → F ou V

Assim, nota-se que não se pode afirmar que Q será verdadeira
[Q e P → (￢ Q) são Verdadeiras] <-> P for Falsa
[V/F e F → F/V ] <-> V

Portanto se "P for F", então "Q e P → (￢ Q)" NÃO são, necessariamente, verdadeiras.

Como pode-se notar na 4ª linha da tabela-verdade, em que P é falsa, mas Q não é verdadeira.
P Q ￢Q P → (￢ Q)
V V F F
V F V V
F V F V
F F V V
Questão mal formulado ou pegadinha. Ele perguntou separadamente Q e P se entao ~q. Não podemos definir se apenas Q é verdadeiro ou falso apenas pelo valor lógico de P.
Essa é minha opinião. Então está errada.
São separadas : O valor de "P" só interfere no valor do ''Q'' da segunda Proposição, a primeira proposição é independente.
Concordo com o colega Luis, se não é possível condicionar um valor lógico para uma premissa individual. Mas pelo visto era uma pegadinha mesmo, pois a banca informa "simultaneamente" ou seja, os valores de Q e da sentença.
Vejo muita gente tentando responder as questões fugindo da tabela verdade.

Tabela Verdade
P Q ¬Q P->(¬Q)
V V F F
V F V V
F V F V
F F V V
A questão não está mal formulada e nem tem pegadinha nenhuma, mas realmente exige uma atenção extra. Verificar que na terceira linha ocorre precisamente o que o enunciado pede: Q = V P --> (¬Q) = V P = F Aqui, muita gente definiu que a questão estaria correta. De fato, "se Q e P --> (¬Q) são verdadeiras, então P é falso".Entretanto, atentem ao ponto-chave da questão, e que justifica que a assertativa esteja errada.
O enunciado afirma que Q e P --> (¬Q) são Verdadeiras se e somente se P for Falsa. Ou seja, "vale a volta" Em outras palavras, o enunciado TAMBÉM afirma que P é Falsa se e somente se Q e P --> (¬Q) são Verdadeiras.
Dai, observamos que na 4a linha da tabela verdade, P é Falsa, enquanto Q não é verdadeira. Dessa forma, justifica-se a assertativa errada Gabarito: E
entre P e Q, nunca haverá resultado V, se pelo menos um for F
Perdoem minha ignorância, já vi e revi as explicações, entendi, porém achei muita forçada de barra.. as duas proposições propostas (Q, P -> ~Q) só serão SIMULTANEAMENTE verdadeiras SE, e somente SE P for F.. a proposição Q é simples, logo o valor já estaria atribuído como V. E o valor da segunda proposição só teria como ser V se P for F. Típica questão CESPE que vale qualquer gabarito. O fato de voltar no Se, somente Se e ver que a segunda proposição não depende do valor de P para ser V, não torna simultaneamente as duas VERDADEIRAS, como condiciona o enunciado.
Essa questão é sem dúvida passível de anulação. A questão mostra claramente duas proposições:
1- Q
2- P -> ~Q
Descomplicando o complicado!
Resolução:
Atribuindo uma proposição simples a cada letra:

Q = Água mole

P = Pedra dura

então,

P -> (~Q) = se a pedra é dura então a água não é mole.

A questão afirma que P = F, então pelo método das primícias falsas, pode ser concluído que

| Água mole (V) |
| Se a pedra dura (F) então a água não é mole (F) |
| Pedra é dura (F) |

Resposta: Quando P é falso, Q e P->(~Q) são diferentes, e não simultaneamente verdadeiras como afirma a questão.

DEUS NO COMANDO!
Para mim, a questão estar certa: ela diz que somente há uma única possibilidade de ambas as proposições serem verdadeira,
sendo P: V.
Se o valor de P já é F, como podem ser SIMULTANEAMENTE verdadeiras? Acho que a banca quis brincar de PEGA! rsrs
Pessoal, a questão é simples!
"As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F."
Q ~>
P → (￢ Q)~>

Se a alternativa conferiu valor F para a proposição "P", então a proposição P → (￢ Q) será V, pois independentemente do valor que"￢ Q" assumir, a proposição composta P → (￢ Q) será verdadeira, certo?
Continuando: repare que na proposição P → (￢ Q), (￢ Q) pode assumir tanto valoração "V", como "F", ou seja, a primeira proposição (Q) pode ser tanto verdadeira quanto falsa, o que contradiz a assertiva, pois nela tem a informação de que, nessas condições apresentadas, as duas proposições terão valor "V", o que é falso.( Se Q pode ser verdadeiro ou falso, não temos como garantir q ela seja verdadeira)
Por isso, questão FALSA!
espero ter ajudado rsrs
Q(V ou F) ^ p (F) -> Q (V ou F) não é necessário que P seja falso, pois há uma contingência.
entendo que se P assume o valor F, não necessariamente as duas proposições serão verdadeiras. porém, o único caso em que as duas proposições serão simultaneamente verdadeiras acontece se e somente se P assumir valor de F. portanto, questão correta a meu ver.

P Q ~Q P->~Q
V V F F
V F V V
F V F V
F F V V
Pessoal, interpretei que a questão disse que Q e P → (￢ Q) seriam verdadeiras se APENAS (= se, e somente se) P fosse FALSA, não APENAS QUANDO P= F. Ou seja, apenas P poderia ter valor F, as demais não. Podemos perceber que Q sendo V, ￢ Q será F. Assim, teremos ambas as proposições verdadeiras (F → F = V), mesmo havendo não APENAS P sendo F. Por isso, o gabarito é ERRADO.
Danilo obrigada pelo Video.
Uma questão que me deixou bastante confuso, mas com o link do vídeo que o Danilo postou ajudou muito, obrigado!
( Quem não conseguiu encontrar nos comentários, o link é esse http://www.youtube.com/watch?v=OUD6GH1nk4I
a partir do 35:17.

Bons estudos e até a próxima.
Mais de 1h resolvendo a questão para chegar à conclusão:

Duas proposições verdadeiras: Q ; P -> (¬Q)

Na proposição P -> (¬Q), para que seja verdade, o valor de "P", necessariamente deverá ser F, pois ¬Q é falso, e nas condicionais, V -> F = F.

Muita gente parou por aí (inclusive eu), mas é preciso analisar também o "Q", já que a questão fala em simultaneidade . Logo, na segunda proposição, independentemente do valor adotado por "Q", sendo "P" falso, a proposição será sempre V.
Usei esse esquema e não sei se é o modo mais correto, porém ele me deu a resposta correta.

Q ^ P --> (~Q)

F ^ F --> ~F

F ^ F --> V

F --> V = V

Na bicondicional (se, somente se) as duas proposições têm que ser iguais para serem verdadeiras, não é o caso.
Questão simples.

Um pré requisito para resolver essa questão é ter o conhecimento da tabela verdade onde apenas "Vera Fischer" é Falso. Trata-se da tabela "Se então".
A => B = Q. (representadas por P => (~Q) no comando da questão)
V V V
V F F *
F V V
F F V
Então, se a questão quer saber se, se e somente P for falso, logo, as proposições Q e P => (~Q) serão simultaneamente V.
Resposta: Como P = F, tanto faz os valores de Q na proposição P => (~Q) pois essa será sempre verdade (segundo a tabela verdade), logo se tanto faz os valores de Q, ou seja, se Q é V ou F, não afetará o valor lógico da proposição. Por fim, Q não será simultaneamente verdadeiro com a proposição P => (~Q) para que a questão seja verdadeira. Errado
Obrigada, Maycon Leite!
ATENÇÃO PESSOAL ! VI MUITOS COMENTÁRIOS EQUIVOCADOS. A RESOLUÇÃO DESTA QUESTÃO ESTÁ EM UM VÍDEO NO YOUTUBE MENCIONADO PELO MAYCON LEITE - VALEU MAYCON.
SEGUE ENDEREÇO DO LINK:
http://www.youtube.com/watch?v=OUD6GH1nk4I a partir dos 35:17.
valeu cris deu pra tirar a duvida de tudo !!!
Obrigada Cris
Salvo engando, grande maioria dos comentários estão contradizendo a propos. Q que sempre será verdadeira e ~Q falsa, logo

a propos. P só pode ser falsa. Note que para ambas propos serem V (Q e P então ~Q), Q(V) e P( * ) então ~Q(f) (V), para P somente e somente se for *F. Não entendi o gabarito, alguem por gentileza comente.
vi o vídeo que a Cris indicou mas não entendi nada mesmo assim acertei a questão com raciocínio errado kkkkkkkk
Gente são 2 proposições: Q é uma e P-> ~Q é outra. Eu acertei a questão por falta de atenção, pode isso? Não vi o negação do segundo Q, pq se tivesse visto com certeza marcaria certo, vi a explicação no vídeo que a Cris postou, mas jamais pensaria assim na hora de resolver... Espero que assim seja na prova quando for errar, amém!
Se mudar o valor do Q para F, a proposição também será V. Logo, não é V somente se o P for F.

Errada.
Comentário em vídeo sobre essa questão em: https://www.youtube.com/watch?v=OUD6GH1nk4I

A partir do minuto 35, 09
O erro da questão é o último F da linha do Q, quando o P é F também.
Questão louca.
Ela não pergunta:
1) As proposições Q e Q->(~P) sempre serão verdadeiras quando P for F.

Ela pergunta:
2) As proposições Q e Q->(~P) serão simultaneamente verdadeiras quando P for F.
A única forma de isso acontecer é se o P for F.
Questão polêmica e de difícil entendimento.
Só aqui que nao estão aparecendo os conectivos? Está um quadrado. To voando
P Q ¬Q P->(¬Q)
V V F F
V F V V
F V F V
F F V V
Se P for F irá mudar....
Não entendi Luiz Eduardo. Se ¬Q for verdadeiro, Q é falso. E a questão quer que Q seja V.
Bom, errei a questão e acho que ela foi bem maldosa. O examinador quer que o "se e somente se" seja entendido como um conectivo lógico. Assim, quando P for falso, necessariamente Q e P->~Q também terão que ser verdadeiros (não só o contrário), onde está o erro da questão. O caso é que o examinador te leva ao erro ao identificar "e" por extenso como não sendo um conectivo lógico, e após o "se e somente se" também por extenso como conectivo lógico. Pura maldade.
Eu errei a questão, demorei um bom tempo para entender o óbvio e que muitos negaram: Aquele "e" da afirmação "Q e P --> ~Q..." É UM CONECTIVO SIM (e não poderia deixar de sê-lo). A única resposta que se aproximou (que empáfia a minha) foi a do Adelar Kempf, pois nem o professor que comentou a questão ajudou muito! Vejam como fica a proposição toda (e que só pode ser dada como certa se todos os valores lógicos forem verdadeiros, caso contrário será uma contigência): [Q ^ (P -->~Q) ] < -- > ~P.
edit: Tentei colocar a tabela verdade aqui, mas ficou toda desconfigurada. Desculpem a caixa alta, mas se você não entendeu a questão, FAÇA A TABELA VERDADE DA PROPOSIÇÃO ACIMA E VERÁ QUE SE TRATA DE UMA CONTINGÊNCIA, logo, gabarito: Errado.
Se o antecedente, na condicional, for falso, a proposição será verdadeira independentemente do consequente.

A->B ( A- antecedente , B- consequente )

ÚNICA FORMA DA CONDICIONAL SER FALSA : antecedente verdadeiro, consequente falso.

No que tange a questão, o Q vai poder ser verdadeiro e falso...logo questão errado.

GABARITO ERRADO
Meu entendimento dessa questão foi o seguinte:
1 - As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F. - nem o primeiro "e" nem o se somente se são conectores nessa questão.
2- No inicio da questão é atribuido valores logicos para P=V e Q=F. Logo na assertiva eu tenho o" Q" isolado como uma proposição simples que é F. Portanto para ele ser V como afirma a questão era só nega-lo (￢ Q) e isso não depende de P ser falso, como afirma a questão
.3 - Esse ponto é o menos confuso: se eu tenho a proposição composta P → (￢ Q) e a segunda parte dessa condicional será verdadeira, tendo em vista que no inicio se atribuiu valor falso para "Q", então (￢ Q) será verdadeiro. Como em uma condicional se o seu segundo termo for V , independentemente do valor de P eu terei uma verdade. Portanto a questão esta toda errada.
Se Q=F , então P ^Q será sempre F.Como a questão fala em simultaneidade, mesmo que ~Q seja V, os valores de Q^P e ~Q não poderão ser simultaneamente V.
CERTO
-----------
Na tabela verdade
P=v
Q=F
¬Q = V
final logico = VERDADEIRO
Assim, não é obrigatório que P seja FALSO para que o valor lógico final da proposição seja verdadeiro.
Segundo professor do vídeo que assisti no youtube esse E não é conectivo, nem o si e somente si, usados apenas para confundir.Q é uma proposição simples e independente da segunda proposição.O fato de p ser falso não influencia em nada o valor lógico de Q, que, a propósito, nem foi dado na questão.
P1 = Q
P2 = P --> ~Q
Obrigue o P a ser FALSO e P2 será V independente do valor de ~Q:
P1 = F
P2 = F --> V
e
P1 = V
P2 = F --> F
P1 e P2 não serão simultaneamente verdadeiras quando o P for obrigatoriamente F.
Gabarito E.
Acredito que a resposta dessa questão foi equivocada, acredito que ela está correta. Ao analisá-la concluo o seguinte: A questão leva-nos a a impor a condição de ambas proposições serem verdadeiras: P1: Q P2: P --> ~Q Assim, considerando-se que P1 é V, para que P2 tenha também de ser V, definitivamente, P terá de ser F, já que ~Q será F, e sabemos que V --> F é F. É minha conclusão.
Refiz 4 vezes a questão e o gabarito sempre o mesmo: CORRETO.
Fui atrás de fontes seguras e a mesma resposta foi dada pelos professores Fabiano Vieira do Aprova Concursos e Cláudio Cabral.

O enunciado traz: As proposições Q e P → (￢ Q), ou seja, são duas proposições: um simples Q e uma composta P → (￢ Q). Esse e do enunciado não é um conectivo lógico, apenas indica que há mais de uma proposição. Mas infelizmente, vai ter candidato que não vai saber diferençar porque proposição lógica não é matemática pura, envolve interpretação (português mesmo!)
Voltando...
O enunciado ainda diz que as proposições Q e a P → (￢ Q), só poderão ser V, se e somente se (bicondição) P=F.
Armando a estrutura: Q,P → (￢ Q)↔P=F. Lembrando que é uma bicondicional, então, P=F, deve ser condição necessária e suficiente.
1)Condição necessária: P ser F
Se P=F, então:
F → (￢ Q)=V.
￢ Q pode ser V ou F, escolho aleatoriamente ser V, logo Q=F e a assertiva estaria errada.
Se escolho ￢ Q=F
F → V=V, e a assertiva estaria correta.
2) Condição suficiente: P não ser F
Se P=V, então:
V → (￢ Q)=V.
￢ Q só pode ser V, logo Q=F e a assertiva estaria errada.
Logo, a única condição para que ambas proposições sejam V é que o P=F!
Gabarito: Correto!
Esse "e" do enunciado (na minha modesta opinião) não deve ser interpretado como conectivo de conjunção. Prova disso é o fato de o texto estar no plural - "As proposições Q e P>(¬Q)" - caso o "e" fosse um conectivo o texto correto seria - A proposição.O se e somente se, quer dizer "unicamente se, só uma maneira de ocorrer, etc".como a questão cita duas proposições: uma simples "Q" e uma composta (condicional) "P > (¬Q)" e que ambas seriam "simultaneamente" V unicamente se "P" for F. Dessa forma teríamos o seguinte:Q=V e substituindo o valor de Q na segunda proposição, P > F = V e isso só poderá ocorrer se P for F.Outra forma de demonstrar ( e essa é irrefutável) é construindo uma tabela-verdade:
P Q ¬Q P-> (¬Q)
V V F F
V F V V
F V F V
F F V V
podemos observar que a única linha onde Q e P-> (¬Q) são simultâniamente V é a 3ª e, nesse caso P de fato é F. Portanto, não posso concordar com o gabarito da questão e para mim o item está C O R R E T O.
Demorei a entender, mas vamos lá pessoal. Vejam se assim conseguem entender também.

É como se o CESPE tivesse combinado duas questões que ela costuma fazer:

Poderia ser assim desmembrado:

1º. Se as proposições Q e P → (￢ Q) são, simultaneamente, V, então P é F. (A afirmativa seria "CERTO").

2º. Se P é F, então as proposições Q e P → (￢ Q) são, simultaneamente, V. (A afirmativa seria "ERRADO")

Juntando a 1ª e a 2ª, chegaríamos a nada menos a questão objeto de discussão, qual seja:

As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F. (A afirmativa é "ERRADO", pois como visto acima, as duas declarações, uma na forma direta, outra na forma inversa, são, respectivamente C e E).

Espero ter ajudado.
No meu modo de ver o erro da questao é o SE SOMENTE SE que determina que somente a preposicao P sendo falsa deixa simuntaneamente as autras verdadeiras...mas não é verdade! caso a preposição P seja verdadeira(simulacao), elas também serao verdadeiras em alguns casos (conforme tabela verdade)...por isso o erro...
Corrijam-me se eu estiver errado: No conectivo SE, E SOMENTE SE as duas proposições devem ter O MESMO VALOR LÓGICO para ser VERDADEIRO. Logo, segundo a questão se P for FALSO, Q necessariamente deveria ser FALSO para que o conectivo SE, E SOMENTE SE fizesse com que a proposição fosse VERDADEIRA.

Porém P -->(~Q) faz com que o Q (antes FALSO) agora seja VERDADEIRO por conta da expressa NEGAÇÃO ~Q = Q. Então, P sendo FALSO e Q sendo VERDADEIRO, as proposições Q e P--> (~Q) NÃO PODEM SER SIMULTANEAMENTE VERDADEIRAS.

Se, e somente se: VV = V \\ FF= V
A questão é bem direta: As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.

Sendo assim, é necessário provar e ida e a volta.

Eu verifiquei apenas a ida e por isso errei. Quando se verefica a volta, fica nítido que Q pode ser V ou F.

Gabarito: Errado
Sou do grupo que está convicto que o gabarito está invertido.

Não consigo contestar explicações perfeitas como a da Natalie Silva e o Josimar Brito.

Não encontrei duas maneitas de, ao mesmo tempo, avaliada a tabela verdade, Q ser verdadeiro e a (P -> ~Q) ser verdadeiro. Somente uma maneira há, que é P sendo falso.
Q P-> ~Q { só encontrei V em ambas na 2ª LINHA, o Q é uma proposição simples e na composta já coloquei a resposta }

V F

V V ======> nesta aqui o P tem valor lógico FALSO

F V

F V

POR QUE ESTA ERRADO O GABARITO??????
POR GENTILEZA reclamem do comentário do professor, PRECISAMOS DE QUESTÕES DE RLM EM VÍDEO. Pagamos por esse serviço.
Que porcaria o comentário desse professor, não é todo mundo que entende esta linguagem técnica que ele faz. Concordo com a Patrícia que já passou da hora de comentários com vídeos!

Gabarito está errado mesmo.

Segue o comentário em vídeo que o nosso amigo I.Duarte postou: https://www.youtube.com/watch?v=OUD6GH1nk4I

A partir do minuto 35, 09
P e Q tem de ser "V".

O comando da questão foi P = falso, ou seja o P NUNCA SERÁ VERDADEIRO... e se nunca será verdadeiro, não tem como P e Q serem Verdadeiros simultaneamente, somente o Q será.
sinceramente Q concursos, esse professor tem vergonha de gravar vídeo? ou vocês que não querem pagar um pouco a mais pra ele gravar vídeo? Muita gente está começando a estudar agora e se depara com umas questões de raciocinio logico e vão ler o comentário do professor e sai sem entender nada nada. Se nós pagamos essa porcaria, nós temos direito de ter pelo menos um pouco de ensino de qualidade.
Fácil de resolver:

Ele dá a condição de P ser apenas falso para a sentença ficar verdadeira, mas caso P seja verdadeiro, também teremos a possibilidade da sentença ser verdadeira quando:

Q(F)eP(V) --> ~Q(F) = V Ou seja, essa já seria uma possibilidade para a sentença ficar verdadeira caso P fosse verdadeiro.

Errada
GABARITO ERRADO

Ficou com dúvida? o comentário da " Dani Concursanda " me ajudou, pode ser que te ajude tbm.

Pra encurtar seu tempo procurando, segue os passos.

clica em - mais úteis - ctrl+f (canto superior do lado direito cola o nome Dani Concursanda) - dar um enter.

Como fala uma colega aqui do Qc: " vamo deixar soar pelo caminho".
O que da pra inferir dessa questão é o seguinte:

P → (￢ Q)
F → (V ou F)
V

Nesse caso "P → (￢ Q)" sempre será verdadeira.
Mas e Q ? Já não podemos dizer o mesmo, pois a questão não traz essa informação e está com uma redação PÉSSIMA!

O cespe adora trazer questões que nem sempre têm respostas, ai você fica 30 minutos tentando adivinhar qual o valor do bendito "Q".
Caramba não entendi até agora... Pra mim deu Gab Certo! Não tendo outra forma das duas proposições darem V ao mesmo tempo... :/
Se P é a proposição inicial e é Falsa, independentemente da proposição Q ser falsa ou verdadeira, essas duas proposições serão verdadeiras... Simples assim..
No meu entendimento:

Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.

Q = verdadeira ou (falsa)

P → (￢ Q) utilizando a bicondicional conforme a questão:

F ↔ F (negação de Q) = V

F ↔ V falsa = F (simutaneamente há possibilidade de ser falsa)
Resolução da questão a partir de 35:12. Veja no link abaixo:

https://www.youtube.com/watch?v=OUD6GH1nk4I

Bons estudos.
Q ^ P - > (~Q)

? ^ f - > ? = V

f ^ ? - > ? = V

pronto.
Melhor forma é separar a bicondicional em duas condicionais pois Q e P → (￢ Q) serem simultanamente V é condição suficiente para P=F, mas P=F não é condição suficiente para Q e P → (￢ Q) serem simultaneamente V, por isso a questão está Errada.
Q e P → (￢ Q)

F ^ F → V = V
V ^ V → F = F
F ^   V → V = V
V ^ F →   F = V

**Existe uma possibilidade em que o P é verdadeiro e o resultado é verdadeiro. Logo, não é apenas quando o P é falso que será verdade! Assim gabarito ERRADO.
ele usou a po "e" de forma escrita e o "se então" por símbolos causando dupla interpretação

errei pq interpretei o "E" sendo apenas um "E" e nao parte da "sentença"
Vi vários comentários divergentes, mas a meu ver o item tá realmente errado.

Não consigo valorar o Q, podendo ser V ou F.

Não consigo afirmar nada.

Ah, o Q é prop simples. Haha
Ótimo comentário da questão nesse vídeo: https://www.youtube.com/watch?v=OUD6GH1nk4I.

Assitam a partir de 35:07.
QUESTÃO: Considerando que P e Q representem proposições conhecidas e que V e F representem, respectivamente, os valores verdadeiro e falso, julgue o próximo item.
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F. ERRADA

DESMEMBRANDO A QUESTÃO...

se, e somente se VV=V E FF=V

Q e P → (￢ Q) = V

Para dar resultado V, anteriormente pode ser FF ou VV. A questão diz que so dará resultado V, somente se um deles der F.

Bom, pelo menos eu fiz assim e acertei :D
Pessoal, o pega é o "e" que age com conectivo ^ [e]. Então fica

Q ^ P → ~ Q ;

Atribuindo verdade para ~Q, temos falsidade para Q e portanto não é possível atribuir valor a "P", não sendo correto afirmar.
P ---> ~Q
(F) (V/F)

A proposição composta vai ser verdadeira independente do valor lógico atribuído à proposição Q, ou seja, Q pode ser V ou F, não tem como eu garantir que as duas proposições serão simultaneamente verdadeiras como diz o enunciado.

GAB: ERRADO
Meu raciocínio:

P1: Q

P2: P -> (~Q)

O examinador diz que se P for igual F (VALOR LÓGICO FALSO), então ambas as proposições acima serão, SIMULTANEAMENTE (AO MESMO TEMPO), V (VERDADE). Vamos testar?

Digamos que Q seja V (já que ele diz isso).

P1: Q (V)                        (V)

P2: P (F) -> (~Q (F))              (V)

Ora, de fato, somente no VERA FISCHER (V -> F) é que a condicional terá valor lógico FALSO. Nesse caso, as proposições P1 e P2 possuem valor lógico VERDADEIRO. Mas vejam a outra possibilidade:

P1: Q (F)                        (F)

P2: P (F) -> (~Q (V))       (V)

Ora, não é porque P é igual a F que, necessariamente, as duas proposições terão simultaneamente valor lógico V, uma vez que Q poderá ser V ou F.

GABARITO: ERRADO.
P Q ¬Q P-> (¬Q)

V V F F

V F V V

F V F V

F F V V
Fiquei meia hora tentando entender

o comentário da dani concusada explica bem

resumindo esqueçam a proposição P o q a questão quer saber é o valor de Q:

p-> ~q = V

para que a proposição seja V P tem que ser F mas Q nao precisa ser somente V pode ser F

então a questão está incorreta pois Q nao tem que ser V pode ser F

o se somente se colocou a questao errada pois limitou Q apenas ao valor V sendo q pode ser F tb ufa kkkkkkkk
Questão CARENTE de boa FORMULAÇÃO, entretanto, se considerar que:

* O "e" do enunciado não é lógico;

* se atentar ao "se e somente se' é o bicondicional

VOCE CONSEGUE FAZER. Monte a tabela VDD e veja que no bi condicional terá UM valor F
ERRADO

Direto ao ponto:

Q e P → (￢ Q)

V ^ F → F = Verdadeiro

V ^ V → F = Falso

F ^ V → V = Verdadeiro

Logo, P pode assumir valor de Verdadeiro ou Falso para ser verdade, e não somente F, como diz a questão.

Bons estudos!!
Q P Q e P -> (~Q)

VV V F F

VF F V F

FV F V V

FF V V V

TABELA, P pode ser verdadeiro tambem para o resultado ser Verdade
Pessoal, vocês não entenderam... No enunciado da questão Q e P ---> (~ Q), esse "e" que aparece entre Q e P não é operador. Se fosse ele estaria no formato de símbolo ^. Além disso, se fosse operador não teríamos duas proposições. Teríamos apenas uma proposição composta e a questão não falaria "As proposições Q e Q ---> (~ Q).

Resumindo, nós temos duas proposições:

P1: Q
P2: P ---> (~ Q)
E elas só serão verdadeiras ao mesmo tempo (simultaneamente) <---> P for Falso.
Ou seja, devido ao "se, e somente se" temos que testar a ida e a volta. Significa dizer o seguinte:

Na ida
P1 é V, logo Q é V
P2 é V, logo P é F, pois, para P ---> (~ Q) ser V , como ~Q é F, P tem que ser F. Então a ida está OK, foi o que ele afirmou.

Na Volta temos que começar pelo P sendo Falso
P é falso. Temos que testar se P1 e P2 são verdadeiros
P2: P ---> (~ Q)
Ora, se P é Falso, não podemos afirmar que (~Q) é falso como no teste de ida. Q pode ser F ou V que a proposição P2 será V.
mas se Q for Falso, então a proposição P1 estará falsa e não vai satisfazer a afirmação da questão, que dizia que ambas eram V.

Por isso, resposta ERRADA
https://www.youtube.com/watch?v=OUD6GH1nk4I

Aos 35 min., tem uma ótima explicação para quem ainda está com dúvidas.
p q ~q p-->(~q)
v v f f
v f v v
f V f V
f F v V
Tem muito comentário errado, vá direto para o comentário do professor.
Questão de difícil compreensão.
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F
Q= V
P-->~Q
F--> F
V
Logo, Q e P → ~Q só são VERDADEIROS QUANDO P=F
Mas, o (se e somente se) quer dizer o seguinte:
Que P é FALSA se e somente se Q e P → (￢ Q) forem verdadeiras. SACOU?
Q=F
P-->~Q
F-->V
V
Logo, P pode ser FALSA mesmo que Q seja FALSA.
Assistam ao vídeo com a correção da questão feita pelo professor Joselias Silva :
Raciocínio Lógico tem que ser comentário por vídeo do professor! Fica a dica Qconcursos!!
o comentário do Ramon segundo está errado. A questão traz Q e P como operação lógica.
Questão maldita. QConcursos comente em vídeo pelo amor de Deus!
Proposições:

Q
P --> (~Q)

Exemplificando:

Q= Maria é dentista. (V)

P= Se João é trabalhador, então Maria não é dentista. (V)
Da para fazer em 10 segundos com o " método Telles "

olhou a questão, viu o sinal da cotoneira significando negação, observou que tem uma seta significando condicional acabou a questão . mantém a primeira proposição e nega a segunda.
Pelo que eu entendi "Q" e "P-> -Q" devem ser simultaneamente verdadeiras, portanto devemos fixar "Q" como tendo valor V. Em "P -> -Q" temos "P -> F" (-Q sempre será F já que Q é V). Portanto P só pode ser F para que "P-> -Q" seja V.
Kkkkk acertei por causa de um comentário de uma questão envolvendo outra matéria. "Se, somente se" deixaria errada a questão pois bem não me recordo o nome do professor que dar macetes de informática das bancas, deu certo kkkk.
No bicondicional (se e, somente se) cabe a ida e a volta

Se P for falso o ~Q pode ser verdadeiro ou falso que a segunda proposição(p->~q) vai ser verdadeira. Logo o valor de Q pode ser V ou F.

Primeira proposição da volta
P -> ~Q
F --> V/F = V
Logo, a segunda proposição da volta (Q) pode ser V ou F, então não dá pra ser simultâneo nessa proposição com o bicondicional.

*errei a questão e demorei uma eternidade para entender isso.
Link atualizado com a resolução:
youtube.com/watch?v=_Wc9UovuVJo desde o início do vídeo (professor Helder Monteiro)
As proposições podem ser verdadeiras, mesmo se p for verdadeiro. Vejamos:
Se Q = F P = V.

Q ^ P -> ~Q
F ^ V -> V
F -> V
V
Difícil entender o que a questão está perguntando...

Mas pensei assim:
P → (￢ Q) Q
1- V V F
2- F V F
3- F F V
4- V F F

Nos 3 primeiros casos a condicional será verdadeira... e o P e o Q podem assumir valores diferentes. Logo, está errado.
Explicação do professor Brunno Lima do Estratégia: https://youtu.be/4HkO5WiBD2I?t=12014
a questão é dificil mais por conta da interpretação de lingua portuguesa do que pelo rlm em si.
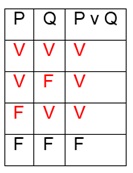
Eu achava que pela tabela daria pra fazer:

P Q ¬Q P->(¬Q)
V V F F
V F V V
F V F V
F F V V

''As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.''

Na tabela marquei de vermelho a única incidência da simultaneidade de "Q" e "P->(¬Q)" serem VERDADEIROS, constatando que nesta linha P = F.
Fiz da seguinte forma,
testando todas hipóteses de Q e P então não Q, para ser verdade:
Q(V) e P(F) ENTÃO NÃO Q(F) = V
Q(F) E P(F) ENTÃO NÃO Q(V)= V
Q(V) E P(V) ENTÃO NÃO Q(F)= F (FUROU A TENTATIVA)
Q(F) E P(V) ENTÃO NÃO Q(V)= V
Conclui-se que temos resultado verdadeiro com o P verdadeiro ou falso. Deixando a questão errada, pois ela afirma que somente se o P fosse falso.
Gabarito errado!
segue correção do GRANCURSOS ... começa em 37:40
Rapaziada, questão simple. Se o Q tiver valor lógico Falso, a negação dele( que é oq está na questão) será Verdadeiro. Com isso, independente do valor de P, a proposição será VERDADEIRA.

Esse "se,somente se" foi só pra confundir mesmo.
Direto e Reto.
Se o valor Lógico de Q for Falso, a proposição será Verdadeira independente do valor de P.
Visto que ~Q = V
É possível verificar que só será possível ter as proposições "Q" e "P->(¬Q)" como verdadeiras simultaneamente se o "P" for FALSO.

Porém, não é isso que a questão afirma, a questão é categórica ao afirmar que caso o "P" seja FALSO necessariamente o "Q" seria verdadeiro, o que não é verdade, isto porque, no "se... então", quando a primeira proposição é falsa, qualquer que seja o valor lógico da segunda proposição, toda a expressão será verdadeira.
Q e P → (￢ Q)
V^F-> (￢V)
F->F=V

Q e P → (￢ Q)
F^V-> (￢F)
F->V =V

A duas possibilidade logo torna a questão errada
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.

Q e P ENTÃO ~Q ---- Não é Se somente se
Analisando o comando da questão por meio de palavras, temos que:
(Q é verdadeiro) e (S é verdadeiro) se, e somente se, (P é falso)

"Se e somente se" significa que temos duas coisas a analisar:
[I] Se Q e P->~Q são ambas verdadeiras, então P é falso.
Isso é fácil de saber que é verdade apenas analisando linha 2 da tabela abaixo. P ser falso é condição necessária para Q e P->~Q serem verdadeiras.
[II] Se P é falso, então Q e P->~Q são ambas verdadeiras.
Qdo P é falso, podemos estar nas linhas 2 ou 4 da tabela abaixo. Na linha 2, realmente, tanto Q quanto P->~Q são verdadeiras, mas na linha 4 isso não ocorre mais. Assim, P ser falso não é condição suficiente para Q e P->~Q serem ambas verdadeiras. Logo: se temos uma condição que é apenas necessária, mas não é suficiente, então o bicondicional não vale.

TABELA (vou chamar P->~Q de X):
P Q ~Q X
V V F F
F V F V [LINHA 2]
V F V V
F F F V [LINHA 4]
Se fizer duas tabelas-verdade fica fácil entender. Quando ele diz "se, e somente se" significa que temos que pegar todas as possibilidades e verificar se é verdade. Para pegar todas as possibilidades, tempo que montar a tabela tanto de um jeito possível, quanto de outro jeito possível (é possível montar uma tabela verdade de dois jeitos diferentes, é só olhar nos comentários que tem gente que monta começando pela primeira proposição, numa tabela de 4 linhas como é o caso, colocando VVFF na primeira e depois VFVF na segunda, e tem gente que monta colocando VVFF na segunda e VFVF na primeira).

PRIMEIRA TABELA (PRIMEIRA OPÇÃO DE TABELA)
P Q P->(~Q)
V V F
F V V
V F V
F F V

SEGUNDA TABELA (SEGUNDA OPÇÃO DE TABELA)
P Q P->(~Q)
V V V
V F F
F V V
F F V

CONCLUSÃO: percebemos que, na primeira tabela, realmente Q e P->(~Q) são simultaneamente V, se, e somente se, P for F. Mas na segunda, quando Q e P->(~Q) são simultaneamente V, P é V e não F.
ESSE GABARITO ESTÁ ERRADO E CABERIA RECURSO, VÍDEO DO PROFESSOR RESPONDENDO A QUESTÃO.

https://www.youtube.com/watch?v=yMLxfJIMqXY

MINUTO 37:40
Até hoje não entendi porque não mudaram o gabarito...
Q^P → (~Q).

Q^P = V. Logo, Q = V e P=V.

Gabarito errado.
Quando temos um "se, e somente se" diante de nós (A↔B) devemos nos perguntar:
1) Se A, então B? (A→B é verdadeiro?)
2) Se B, então A? (B→A é verdadeiro?)
Se a resposta for "sim" a ambas as perguntas, e tanto A→B e B→A forem V, então A↔B será verdadeiro também.

Diz a assertiva que Q e P→(-Q) serão ambas verdadeiras se, e somente se, P for falso
Aqui então caberão as duas perguntas novamente:
1) Se Q e P→(-Q) forem ambas verdadeiras, então P é falso? A resposta aqui é sim. Há só uma ocorrência simultânea de Q=V e P→(-Q)=V, e nessa única ocorrência temos que P=F
Q | P | P→(-Q)
V---V----F
V---F----V
F---V----V
F---F----V
2) Se P for falso, então Q e P→(-Q) são ambas verdadeiras? A resposta aqui é não. Há duas ocorrências de P=F na tabela-verdade, e em apenas uma delas as outras duas premissas são ambas verdadeiras.
Q | P | P→(-Q)
V---V----F
V---F----V
F---V----V
F---F----V (a hipótese que invalida a assertiva)

Gabarito E. Questão bem difícil de ser lida e interpretada.
Acertei , mas a questão foi mal formulada. Redação estranha.
Eu entendi na pergunta que Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.

Ou seja, na linha marcada de vermelho, então dei verdadeiro..

P  Q  ¬Q    P->(¬Q)
V  V   F      F
V  F   V      V
F  V   F      V
F  F   V      V
Há a possibilidade de P ser verdadeiro e a proposição composta continuar verdadeira, por isso a questão está ERRADA.
Quando isso ocorre:
Q ^ P → (~ Q), caso Q for falso e P for verdadeiro a proposição continuará VERDADEIRA:
F ^ V → V = VERDADEIRO
Se Q e P forem = V logo teremos um resultado FALSO
Se somente P for = V teremos um resultado VERDADEIRO....porém caso somente Q seja F ou ambos sejam F, teremos também proposições verdadeiras.

Logo a questão está errada

Errei a primeira vez que fiz pois parei no somente P, esquecendo de testar o Q como Falso
Eu acho que, além de tudo, o que a gente pode levar como aprendizado de uma questão dessas é o fato de que a gente deve ver o enunciado como uma proposição composta.

O nosso raciocínio de imediato é pensar da seguinte forma:

Q = V e P -> (~Q)= V -> P = F;

Então, na verdade, quando lemos a questão, lemos da seguinte forma:

A proposição P é falsa se as proposições Q ^ P-> (~Q) forem simultaneamente verdadeiras.

*o se, então está invertido;

Dessa forma a questão se mostraria verdadeira, mas notem que a ordem está invertida e, além do mais, há uma bicondicional na assertiva:

Q ^ P-> (~Q) <--> P;

Sendo uma bicondicional uma condicional que "aponta" para os dois lados, isso é igual a:

P-> {Q ^ P-> (~Q)} => F -> V ^ V (Se P for falso, então Q e P-> (~Q) podem ser verdade, porque teremos um resultado = verdade);

{Q ^ P-> (~Q)} -> P => V ^ V -> F (Se Q e P-> (~Q) forem verdade, então P não pode ser falso, porque a condicional seria falsa; portanto gab. errado);

Não quero justificar, já justificando, o gabarito da banca, mas o que importa é ter a questão em mente, porque, eventualmente, ela pode se repetir em prova, ou vir alguma muito parecida.

Abrçs.
As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F.

Comentário Objetivo: A questão quis dizer o seguinte: se a Proposição P for F, a proposição Q só pode ser V simultaneamente ?

Não, ela pode ser tanto V quanto F !! que a proposição P → (￢ Q) será V

Se Q=V
P-->(~Q) = F-->F = V

Se Q=F
P-->(~Q) = F-->V = V

ou Seja não será necessariamente verdadeira, ela pode ser falsa e não mudará o valor lógico
O que pegou foi esse enunciado que botaram pra lascar. Depois de ficar de cabeça pra baixo tentando entender e aprendendo com os comentários dos nobres colegas eu entendi assim:
P-----> ( ~Q )
?------> ( V )= V
F/V----> ( V )= V
A tal da simultaneidade é que tanto faz dar F ou V.

Se houver algum erro por minha parte peço desculpas e agradeço se me corrigirem.
Certo!

https://www.youtube.com/watch?v=yMLxfJIMqXY minuto 37:42

Curte aqui para o comentário ficar nos mais curtidos e dessa forma facilitar o acesso para quem teve dúvida.
Entendi da seguinte maneira:
O conectivo <-> (se somente se) será verdadeiro em 2 situações:
F <-> F = V
V<-> V = V
A QUESTAO DIZ: As proposições Q e P → (￢ Q) são, simultaneamente, V se, e somente se, P for F
Não necessariamente, ela pode ser V (TAMBEM) se, e somente se, P for V
VÁRIOS COMENTÁRIOS ESTÃO ERRADOS

ENQUANTO VOCÊ TA AÍ FAZENDO TABELA VERDADE TEM GENTE JÁ SE AQUECENDO PARA O TAF!!!

ENTENDA A QUESTÃO:

A QUESTÃO EXIGE: O "Q" E "P → (￢ Q)" SEJAM VERDADEIROS SIMULTÂNEAMENTE
ENTÃO VOCÊ NÃO PODE ATRIBUIR QUALQUER VALOR PARA O "P"
EXEMPLO:

O "Q" É OBRIGATÓRIAMENTE VERDADEIRO ENTÃO A EXPRESSÃO "P → (￢ Q)" PARA SER VERDADEIRA IGUAL O ITEM FALA SÓ SENDO COM O "P" FALSO POIS SE O "P" FOR VERDADEIRO A EXPRESSÃO SERÁ FALSA , E O QUE A QUESTÃO DIZ É QUE AS DUAS DEVEM SER VERDADEIRAS ENTÃO A ÚNICA SOLUÇÃO É ESSA, O GABARITO DESSE ITEM ESTÁ ERRADO,

A RESPOSTA CERTA É GABARITO CORRETO.
fiz 4x e "errei" as 4. n faz sentido nenhum
Fonte:projeto_1902
As proposições Q e P → (￢ Q) são, simultaneamente(NÃO), V se, e somente se, P for F. (ERRADO)
- P1: Q ^ P → (~ Q)
V ^ V → F
V → F => F
- P2: Q ^ P → (~ Q)
F ^ F → V
F → V => V
- P3: Q ^ P → (~ Q)
V ^ F→ F
F → F => V
- P4: Q ^ P → (~ Q)
F ^ V→ V
F → V => V

ATENÇÃO!!!
#Em nenhuma das formas tentadas as proposições R: b:Q ^ a:P e ~b: (~ Q) são simultaneamente verdadeiras, independente de P ser F ou V.
- P1: V → F => F
- P2: F → V => V
- P3: F → F => V
- P4: F → V => V
- P5: V→ V => V impossível ambas as proposições serem verdadeiras de forma simultânea
Só desenhar a tabela verdade da proposição.

ID

1060465

Banca

CESGRANRIO

Órgão

PC-DF

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Considerando que P e Q representem proposições conhecidas e que V e F representem, respectivamente, os valores verdadeiro e falso, julgue o próximo item.

Se P for F e P V Q for V, então Q é V.

Alternativas

Certo

Errado

Comentários

Tabela Verdade do OU
V ou V/ F ou F = F
V ou F/ F ou V = V
Conjunção: é verdade quando tudo for verdade.
Disjunção Inclusiva: é falso quando tudo for falso.
Condicional Simples: é falsa quando o 1º for verdade e o 2º falso (Dica: Vera Fischer = Falsa).
Bicondicional: é verdade quando os valores lógicos forem iguais.
Disjunção Exclusiva: é verdade quando tiver um ÚNICO verdade.
P >>F
P V Q>>>V
F V V>> V
Logo Q>>> V
Caro(a) NMS, seu comentário contém um equívoco:
Tabela Verdade do "OU":
P Q V
v v v
v f v
f v v
f f f
Assim:
Se (P v Q)é v, então Q é V.
No conectivo "ou" se as duas forem falsas ele tem valor logico F, sendo assim, neste caso o que tem que ter valor lógico V pois foi dito no enunciado que P tem valor lógico F, e afirma também que a primeira proposição (PvQ) tem valor logico V.
Jogando na segunda proposição: No conectivo "se, então" se a primeira for V a segunda tem obrigatoriamente que ter valor lógico V, para a proposição ser verdadeira.
A questão é simples: se a proposição composta pelo conectivo OU (disjunção) for P V Q, e que para que esta proposição seja verdadeira, deve-se que pelo menos uma das proposições simples seja verdadeira, se as duas forem falsas, então seu resultado será falso. Como a questão já informou que P é falso, então para que a composta seja verdadeira, a proposição simples Q é verdadeira, estando certa a afirmação.
P Q P v Q

V V V

V F V

F V V

F F F
F V = V
P v Q
É possível utilizar o princípio da argumentação lógica?:
P(f)
P(f) ou Q(v),
______________
Logo, Q é (V)
Ja foi explicado mas acredito que posso simplificar mais:

No uso do "OU" se houver alguma proposição "v", a composição será "v". Facil assim!
A disjunção só será falsa caso todos os valores forem falsos.
Na disjunção inclusiva, basta um V pra ser verdade.
A questão está perguntando se a sentença P V Q for VERDADE , então Q É OBRIGATORIAMENTE VERDADE TAMBÉM.

1º Observar os dados que a questão fornece:
No começo da questão, porém, ela já afirma que : Se P for F = Logo a questão diz que P é FALSO

2° Sabendo-se que P é falso basta analisar a sentença.
P V Q = o conectivo utilizado é o "V = OU". Precisamos lembrar que no "OU" a proposição só será falsa quando as 2 proposições forem falsas! Logo...Q SERÁ OBRIGATORIAMENTE VERDADE, pois se Q fosse falso ficaria = P V Q = F
Gabarito. Correto.
P Q PvQ
V V V
V F V
F V V
F F F
No conectivo Ou, basta um ser V para o resultado ser V.
Bons estudos!
EU ENTENDI ASSIM: P JA É FALSO ENTAO PARA O Q SER VERDADEIRO A UNICA POSSIBILIDADE NA DIJUNÇÃO NA TABELA VERDADE E DE FouV=V......ENTAO SE P É FALSO E PVQ E VERDADEIRO....NO SE ENTAO TEMOS SOMENTE VERDADEIRO......
~p^p->q= v
Simples assim.
A questão diz: Se P for F
P = F
e que P v Q for V
P v Q = V
assim fica substituindo o P por F
F v Q = V
Na tabela da disjunção F com V resulta em V.
Portanto Q é V
Resposta CERTO
Simples assim.
GABARITO: CERTO
O "v" é verdadeiro (V) quando pelo menos uma proposição for verdadeira.
P v Q = V
F v ? = V
Então, Q Sendo F
F v F = F
Q sendo V
F v V = V
Logo Q deverá ser V para que o resultado final de Verdadeiro.
Pela tabela-verdade da disjunção:

Vemos que pela tabela-verdade, se P for F e P V Q for V, então Q é V.

RESPOSTA: CERTO
A Disjunção Inclusiva ("v") é verdadeira quando, pelo menos, uma de suas proposições for verdadeira.

P Q P v Q
V V V
V F V
F V V
F F F
Descomplicando!

Resolução:
Atribuindo uma proposição simples a cada letra:

Q = Água mole

P = Pedra dura

então,

P OU(v) Q = pedra é dura OU água é mole.
A questão afirma que P = F, então pelo método das primícias falsas, pode ser concluído que
| Água mole (V) |
| Pedra dura (F) OU água mole (V) |
| Pedra dura (F) |
Resposta: Quando P é falso, Q tem que ser verdadeiro para fazer com que a sentença tenha um valor lógico verdadeiro. No conectivo OU basta uma das proposições ser verdadeiro para que toda a sentença assuma valor lógico V.

DEUS NO COMANDO!
Se P for FALSO e P ou Q for verdadeiro, então Q é verdadeiro?
Traduzindo, ele quer saber se:
P sendo FALSO e Q sendo Verdadeiro o P v Q será mesmo verdadeiro: SIM!!!
Gente, é simples:
Olha a tabela verdade do "ou"
V v V= V
V v F= V
Falso ou Verdadeiro = Verdade
F v F= V
Questão bem simples:
O conectivo ou (v) só será FALSO se as duas proposições que o compõem forem FALSAS. Sendo assim, como a proposição P V Q é verdadeira e P é falso, a proposição Q só poderá ser VERDADEIRA

Item correto
No conectivo OU, pelo menos uma deve ser V para que seja verdadeira.
Sabendo que p=F, obviamente q=V, pois é única maneira da expressão ser verdadeira.
Se P fosse V e P v Q fosse F, aí sim Q seria F, vejamos:
pois aí meus queridos, entraria a Vera Fischer pra invalidar a novela da Reeeeeede Globo.

Dê um like nesse meu comentário e corre pro abraço môô quirido (a).

Gab: C
eu acho que deveria ser escrita P v Q e não P V Q
Gabarito: Certo
Mas, esse simbolo da disjunção (V) maiúsculo, atrapalhou muita gente!
concordo Kely, ai fica difícil saber se é um conectivo ou um valor Verdadeiro... kkk
nossa, fiz a maior confusão na hora de montar....não acredito que errei !! =(
mas existe uma possibilidade de ser falso e mesmo assim seria verdadeira!!!! eu entraria com recurso para anular essa questão.
P^(PvQ)->Q
F e V -> V
f->V
Logo: questão certa! :)
Fazendo a tabela verdade chega lá
Correto.
Não precisa fazer a tabela verdade. Basta saber a lógica dos conectivos.

No enunciado afirma-se:
P é falso.
P V Q é verdade. Como se trata de uma disjunção ( ou ) será falso quando ambas as proposições forem Falsas. Logo, se toda a estrutura é VERDADE, como afirma a questão, Q só pode ser Verdade, uma vez que, se o mesmo for Falso, toda a estrutura P V Q será FALSA, invalidando a questão.
cheguei ao resultado com a tabela verdade dos conectivos "ou" e "se... então"
Muito tranquilo. Se P tem o valor Falso, logo, para que a proposição seja V, Q tem que ser V.
P(F)vQ(?) = V.
F com F dá F
F com V dá V. Conectivo OU, Basta um V para ser V
se...então
Só dá FALSO de V pra F
começou com afirmativa Verdadeira pode saber que a resposta na (condicional se.. .então é FALSA)
NA DISJUNÇÃO (OU ) , PELO MENOS UM TEM QUE SER VERDADEIRO, PARA QUE SEJA (V)
Betânia CVo, ou seu comentário ta errado ou esse comentário é de outra questão.
Esse v maiúsculo acabou me atrapalhando.
esse (V) maiúsculo filha da !@#$%¨&
Pessoal, é só lembrar que é verdade que o Flamengo tá na frente do Vasco. Então sempre que F vier na frente de V, a sentença é verdadeira. Por isso gabarito CERTO. Desculpem os vascainos KKKKKKKKKKKKKKKKKKKKKKKK
Vale lembrar que esta regra só vale para SE ENTÂO
Pessoal não estou entendo o fato de usar-mos o resultado do conectivo OU (V) como resposta, onde fica o enunciado do se...então?
CERTO.
-------
Na tabela verdade
P - Q (P v Q)
V V V
V F V
F V V
F F F
-------
Assim, se P é falso e o valor lógico de P v Q = V, "Q" só pode ser VERDADEIRO.
Não precisa de Tabela Verdade, penso eu.

P é FALSO

PvQ é VERDADEIRO

Então o PvQ é VERDADEIRO pois o conectivo OU (v) exige que apenas uma das proposições sejam VERDADEIRAS para que a outra também seja (P: FALSO Q: VERDADEIRO) > Verdadeiro v Falso = VERDADEIRO
se P é falso obrigatoriamente Q tem que ser verdadeiro para a dijunção OU ser verdadeira . Visto que na conjunção OU \/ basta que um elemento seja Verdadeiro para que a proosição seja verdadeira. ele afirmou que P é Falço então necessariamente Q teria de ser Verdadeiro para P\/Q ser verdadeira.

Força e Honrra . Venceremos Kuwabara nos ajudara.
P ^ (PVQ) ->Q

F ^ V -> V

F -> V

V
Disjunção V ( só um "ou") só será falso quando todos valores forem falsos.

Se a questão diz que a proposição é Verdadeira e P é falso, logo Q tem que ser verdadeiro para que o valor lógico da proposição seja V.

Se Q fosse F, F com F daria F.
Essa tá mal feita, porque eu confundi P v Q com PVQ. mas mesmo assim acertei fazendo com a disjunção
questão mal feita da porra...
GABARITO CORRETO.
P v Q = V
F v V = V
V = V
Vá direto na explicação do professor.

Gab. Certo.
Esse foi o meu entendimento: Utilizei a lógica da condicional com a conjunção, resolvendo-a de acordo com a ordem de precedência das operações lógicas. Me corrijam se eu estiver errado.

V e V -->V=
V-->V= V
Espero que depois de 53 comentários alguém visualize rs

Galera basta o preenchimento conforme a questão passa às informações:

Se P for F e P V Q for V, então Q é V.

F ^ V ------> Q= V

Somente será falso no se então nas circunstâncias de VF , ou seja Verdade
para resolver basta fazer a tabela verdade.

na terceira linha vai dá:
P Q P v Q
F V V
P é F
P v Q = A junção dos dois tem que ser V

Substituindo o P:
F v Q = Para que essa sentença fique verdadeira, basta substituir o Q por V
F v V = V (O conectivo "ou (v)" é aquele cara paz e amor (lembra do símbolo "paz e amor"), basta que um seja V para que toda a sentença seja V)
Eu fiz assim e cheguei no resultado, acho que meu pensamento está correto e espero ter ajudado.

ID

1062646

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2012

Provas

CESGRANRIO - 2012 - Petrobras - Analista de Sistemas Júnior - Processos de Negócios-2012

Disciplina

Raciocínio Lógico

Assuntos

A negação da proposição “Todo professor de matemática usa óculos” é:

Alternativas

Nenhum professor de matemática usa óculos.

Ninguém que usa óculos é professor de matemática.

Todos os professores de Matemática não usam óculos.

Existe alguma pessoa que usa óculos e não é professor de matemática.

Existe algum professor de matemática que não usa óculos.

Comentários

Proposições categóricas
Negação de Todo é:
Algum ...não ou Existe algum....não
LETRA E)
valeu professor pela resposta
Expressão: Todo A é B
Negação:
Algum A não é B
Existe A que não é B
Pelo menos um A não é B
Nem todo A é B
É sabido que ao se negar uma proposição com o quantificador "TODO", trocamos o mesmo pelos

quantificadores "PELO MENOS UM" ou "EXISTE ALGUM" e trocamos o sentido da proposição.

Assim a negação da proposição “Todo professor de matemática usa óculos" é:

Existe algum professor de matemática que não usa óculos.

Resposta : E
Sempre que tiver pedindo alguma negação na frase, lembre-se de PEA+NÂO
Pelo menos
Existem
Algum
mais o "Não" na frase de negação.É mais prático pra anular a frase e chegar na correta.
Se pelo menos UMA pessoa que seja professor e não use oculos, ja estara negado a proposição. Sucesso nos estudos e não desistam, mesmo que demore, acreditem em Deus, e em sí mesmo.
Negação do "TODO"
PEA + NAO
P - (Pelo menos um)
E - (Existe um)
A - (Algum)
-------------------------------------------------------------------------------------
Negação do “ALGUM” ---> Válido para qualquer um do PEA
NE TO + NÃO
Nenhum Todo + Não
-------------------------------------------------------------------------------------
Negação do “NENHUM”
PEA
-------------------------------------------------------------------------------------
Letra E.
e) Certo. Basta encontrar algum professor que não use óculos para furar a ideia.

Questão comentada pelo Prof. Márcio Flávio
RESOLUÇÃO:

Para negarmos que todo professor usa óculos, basta encontrarmos um contra-exemplo, ou seja, ALGUM professor que NÃO usa óculos. Temos isto na alternativa E.

Resposta: E
Gabarito E
Basta encontrar algum professor que não use óculos para furar a ideia.

ID

1062652

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2012

Provas

CESGRANRIO - 2012 - Petrobras - Analista de Sistemas Júnior - Processos de Negócios-2012

Disciplina

Raciocínio Lógico

Assuntos

Dadas as premissas p₁ , p₂ ,..., p_n e uma conclusão q, uma regra de inferência a partir da qual q se deduz logicamente de p₁ , p₂,..., p_n é denotada por p₁ , p₂ ,..., p_n ├q. Uma das regras de inferência clássica é chamada Modus Ponens, que, em latim, significa “modo de afirmar”. Qual a notação que designa a regra de inferência Modus Ponens?

Alternativas

p ∨ q, ¬p ├ q

p ∧ q, ¬p ├ ¬q

p ↔ q ├ p→q

p, p → q ├ q

q, p → q ├ p

Comentários

Modus Ponens
P -> Q
P
---------------
P
eu em, ta amarrado kkkkkkkkk
Bote fé Matheus Sales ..heheheehehehehehehehe
Tomar banho de sal grosso Matheus e Fred! hehehehehe
ééé gente, é rir pra não chorar kkkkkkkkkkkkk
Que trem é esse? É de passar no pão?!!!
Essa foi para torar.... Meus deus
A regra de inferência, Modus Ponens, pode ser simbolizado formalmente da seguinte forma:

Sendo que A regra Modus ponens pode ser escrita na forma de sequentes como é mostrado a seguir:

Analisando as alternativas, vemos que a correta é a letra D.

Resposta: Alternativa D.
Que isso
Nossa!!!!
Fácin... Sempre que vier na prova "Modus Ponens" Atente-se logo para a condicional!!
O termo antecedente é verdade se o consequente também for.
Se P implica em Q e P é verdadeira, então Q é verdadeira. Um exemplo é:
Se estiver chovendo ( P )
Encontrarei você no cinema (Q)
Se estiver chovendo, eu encontrarei você no cinema.
Está chovendo.
Então, encontrarei você no cinema.

P ---> Q, P
-----------------
.:. Q

Mesma coisa da letra "D" . É só atribuir alguma frase ou hipótese.

LEMBRANDO QUE O SIMBOLO >> |- Não é uma negação, e sim como se fosse uma divisão.
Não entendi nem com a explicação do nosso colega, kkkkkk

Fico com a resposta que é de passar no pão! Alguém socorre!!!
Gente do céu! hahahaha
Esse início aí cheio de bobagens no enunciado é só pra intimidar o candidato. O modus ponens é simplesmente: se P é verdade, Q também será verdade. Se P for falso, Q também será falso. Já no modus tollens, ocorre o contrário: se Q for verdade, Q também será verdade. Se Q for falso, P também será falso.
RESOLUÇÃO:

Observe a condicional p -> q. Para esta condicional ser verdadeira, sabemos que:

- se pudermos AFIRMAR que p é V, então concluímos que q também precisa ser V (caso contrário cairíamos numa condicional falsa). Este é o Modus Ponens, ou modo de afirmar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: p
Conclusão: q
Resumindo o modus ponens em uma linha: p, p->q |- q (letra D).

- se pudermos dizer que a NEGAÇÃO de q é V (ou seja, q é F), então concluímos que p precisa ser F também (caso contrário cairíamos numa condicional falsa). Isto é, concluímos que ¬p é V. Este é o Modus Tollens, ou modo de negar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: ¬q
Conclusão: ¬p
Resumindo o modus tollens em uma linha:¬q, p -> q |- ¬p.

Resposta: D
Observe a condicional p -> q. Para esta condicional ser verdadeira, sabemos que:
- se pudermos AFIRMAR que p é V, então concluímos que q também precisa ser V (caso contrário cairíamos numa condicional falsa). Este é o Modus Ponens, ou modo de afirmar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: p
Conclusão: q
Resumindo o modus ponens em uma linha: p, p->q |- q (letra D).
- se pudermos dizer que a NEGAÇÃO de q é V (ou seja, q é F), então concluímos que p precisa ser F também (caso contrário cairíamos numa condicional falsa). Isto é, concluímos que ¬p é V. Este é o Modus Tollens, ou modo de negar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: ¬q
Conclusão: ¬p
Resumindo o modus tollens em uma linha:¬q, p -> q |- ¬p.

Resposta: D
Não tinha a mínima ideia dessa
Colocar a fórmula na horizontal quebrou minhas pernas :/ fiquei perdida kkkkk

ID

1066933

Banca

IBFC

Órgão

SEPLAG-MG

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Se o valor lógico de uma proposição P é verdadeiro e o valor lógico de uma proposição Q é falso, então é correto afirmar que:

Alternativas

o condicional entre P e Q , nessa ordem, é verdade.

a disjunção entre P e Q é verdade.

a conjunção entre P e Q, nessa ordem, é verdade.

o bicondicional entre P e Q, nessa ordem, é verdade.

Comentários

Letra B correta
P: Verdade
Q: Falsa
P v Q = Verdade
Condicional ( SE..ENTÃO) -> SÓ É FALSO QUANDO V - F (nessa ordem)
Disjunção ( OU ) V Só é FALSO SE AS DUAS F-F
Conjunção ( E ) ^ SÓ É VERDADE SE V-V
Bicondicional ( Se, e Somente Se) <-> Só é verdade se F-F ; V-V

A questão nos deu V-F
a) na condicional FALSO
b) na disjunção VERDADEIRO (resposta correta)
c) na conjunção FALSO
d) bi condicional FALSO
Condicional P -> Q; Verdadeiro se...então Falso = Falso
Disjunção P v Q; Verdadeiro ou Falso; Verdadeiro ou...ou Falso = Verdadeiro
Conjunção P ^ Q; Verdadeiro e Falso = Falso
bicondicional P <-> Q; Verdadeiro se e somente se Falso = Falso
Na disjunção: Basta um ser verdadeiro pra ser verdade.
Maldade da banca ein !!!
Na conjunção para ser verdadeiro, tudo verdade.

na disjunção, para ser falsa,tudo teria que ser falso.
Bicondicional para ser falso,verdadeiro e falso (vice-versa)
Gabarito. B.
P -> Q P v Q P ^ Q P<->Q
v F => F V F => V V F = F V F => F
LOGO só seria verdadeiro a disjunção
Na Disjunção Inclusiva toda vez que vinhar V, a sentença sempre será verdade.

Atenção:
cuidado para não confundir com a Disjunção Exclusiva, na qual a sequência V/F= é Falso... sendo as outras todas verdades.
Questão Top demais!
GABARITO: B
O "v" é verdadeiro (V) quando pelo menos uma proposição for verdadeira.
A) V>F=F
B)VvF=V
C)V^F=F
D)V<>F=F

GABARITO ''B''
Esta questão trata-se de uma aplicação direta da Tabela-Verdade.

Verifica-se na Tabela-Verdade que considerando P tendo valor VERDADE e Q valor FALSO, a disjunção entre P e Q é verdade.

RESPOSTA: B
V,F para a disjunção é verdadeira.
P=V e Q=F
a) o condicional entre P e Q , nessa ordem, é verdade. V ->F= F
b) a disjunção entre P e Q é verdade. V v F = V
c) a conjunção entre P e Q, nessa ordem, é verdade. V ^ F = F
d) o bicondicional entre P e Q, nessa ordem, é verdade. V<> F = F
Somente se encaixa na resposta, a disjunção, já que ela para ter o seu valor lógico verdadeiro só é necessário que tenha pelo menos uma preposição verdadeira. Gabarito: B.

Bons estudos e até a próxima!
Macete que criei...
ou...ou...: ≠ = V
bicond: = = V
Letra: B
a) V -> F = F
b) correta
c) V ^ F = F
d) V v F = F
De 2013 para 2015 o grau de dificuldade aumentou bastante, quem dera ainda fosse simples assim.
disjuncao = ou - com uma proposicao V já torna Verdade ou de aboubado
conjuncao = e - todas as proposicoes precisam ser V para ser Verdade E de exigente
condicional = se entao - apenas no caso de respectivamente as proposicoes forem V e F , nessa ordem, o resultado será Falso. Vera Fisher é falsa
bicondicional = se e somente se - no caso das duas proposicoes terem o mesmo valor F e F ou V e V o resultado será Verdade. bicondicional só fica feliz com um igual
Gab B

uma questao similar Q757803

ID

1067515

Banca

CESPE / CEBRASPE

Órgão

STF

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Julgue os itens seguintes, relativos à lógica proposicional.

A sentença “A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura” pode ser corretamente representada na forma P→Q, em que P e Q sejam proposições simples convenientemente escolhidas

Alternativas

Certo

Errado

Comentários

ERRADA
P -> (Q^R)
Deve ser representada (P ^ Q)
o erro está na parte que diz proposições simples, pois as duas situações ( excelência e grande experiência na magistratura ) obrigam ao uso de uma proposição complexa do tipo p -> ( q ^ r )
O erro da questão está em convenientemente escolhidas. Na implicação há uma relação entre suficiência e necessidade.
As duas proposições são simples: a primeira - Se um currículo demonstra ......, então a indicação de juízes...
Na verdade o erro da questão é que temos apenas uma proposição simples e não duas proposições simples.
Proposição Composta ligada pelo conectivo "e"
"A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura"
Representação simbólica: P ^ Q
Conclusão:
Questão errada pois a questão apresenta simbolicamente P -> Q ( condicional P então Q)
X é condição antecedente. Y é condição consequente.
X: 'um currículo que demonstre excelência e grande experiência na magistratura'.
Y: 'A indicação de juízes para o STF'.
Logo: 'Um currículo que demonstre excelência e grande experiência na magistratura' é condição necessária para 'A indicação de juízes para o STF.'
Temos então:
(P^Q)->R
Questão errada.
Resposta correta: P ^ Q

p ^ q = e = Conjução
p v q = ou ( disjunção)
¬p= não (negação )
p-->q=se...,então...( condicional)
p<-->q = ...se e somente se ...( bi-condicional)
Trata-se de uma preposição simples que induz as pessoas a pensarem que é uma preposição composta regida pelo conectivo " ^ ".
Ilustrando o que a colega Habib souza comentou:

QUESTÃO ERRADA
Proposição Simples: P
Afinal, qual a resposta correta?? Aff.
Gabarito. Errado.
possui a conjunção
seria =>
P ^ Q
Questão ERRADA
O correto seria Q -> P

P -> Q (é uma CONDICIONAL) "Se..., então.." (ou seja, não podem comutar! )
Se "P" então "Q".
"P" (antecedente) -> "Q" (consequente)
"P" é condição suficiente
"Q" é condição necessária
"Q" é condição necessária para que o "P" ocorra.
ERRADA.
Vamos analisar a Proposição:
A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura
Relação de causa consequência
- P = A indicação de juízes para o STF (causa)
- Q = um currículo que demonstre excelência (consequência/efeito)
- R = grande experiência na magistratura
Os conectivos encontrados em negrito representam a proposição na forma a (P->Q) ^ R
Bons Estudos!!
Ou vc podem pensar que a lógica não tem nada a ver com o Português, e como tem um "E" ali no meio, tá errado e é conjunção é ponto final.
Errado
Poderia ser P ^ Q
A questão está ERRADA, porque para unir as duas proposições temos o conectivo “e” que representa uma conjunção e seu símbolo é ^ (um V de cabeça pra baixo). A representação correta seria p^q.

A representação p->q é uma condicional, a qual é representada pelo conectivo “se”, “então”.
Primeiramente, vamos separar as proposições, lembrando que a letra E em “...demonstre excelência e grande experiência...” não é um conectivo lógico, pois não está unindo duas proposições simples, logo:

P: indicação de juízes para o STF

Q: um currículo que demonstre excelência e grande experiência na magistratura.

Assim, para que possamos corretamente representar com uma condicional, deve-se escrever como:

Se um currículo que demonstra excelência e grande experiência na magistratura então haverá indicação de juízes para o STF.

Que ficaria Q ➔ P.

Resposta: Errado.
A questão apresenta 3 proposições e 2 conectivos explícitos ("consequência" e "e").
P= A indicação de juízes para o STF
Q= currículo que demonstre excelência
R= grande experiência na magistratura
Daí podemos concluir que a expressão P→Q não representa as proposições do enunciado. Seria necessário incluir uma conjunção (^) para representar o "e".

Gabarito: Errado
Se um currículo que demonstra excelência e grande experiência na magistratura então haverá indicação de juízes para o STF.

Que ficaria Q ➔ P.
Resposta Errada
Além de estar errada a assertiva lógica, a própria informação jurídica está errada. Para ser ministro do STF, não é preciso ser juiz. Basta ter Q.I. (quem indica) e ter "notório saber jurídico", que é algo, digamos, relativo e convencional. O exemplo disso é o próprio ministro do STF Dias Toffoli, que nunca foi juiz (reprovou em todos os testes de Magistratura), mas era advogado do PT e, ainda, assumiu a presidência do TSE e, inclusive, atuou nessas eleições... Pouco suspeito... Enfim...
No meu entendimento, o erro não está no fato de o certo ser Q -> P no lugar de P -> Q.
O enunciado diz que "em que P e Q sejam proposições simples convenientemente escolhidas". Dizendo isto ele não indica qual proposição vai ser P ou Q, assim tanto faz Q -> P ou P -> Q.
O erro está no conectivo "e", que diferente do que alguns disseram, está sim conectando duas proposições simples, pois "um currículo que demonstre excelência" e "grande experiência" podem cada uma assumir um valor de Falso ou de Verdadeiro.
Essa é a minha leitura. Não sei se está equivocada.
Concordo com a Fernanda... Dessa forma, Q é uma proposição simples (Juizes serão indicados para o STF) enquanto P é uma proposição composta (Se o Juiz possui um currículo que demonstre excelência e grande experiência na magistratura)
Julgue os itens seguintes, relativos à lógica proposicional.

A sentença “A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura” pode ser corretamente representada na forma P→Q, em que P e Q sejam proposições simples convenientemente escolhidas

Um currículo que demonstre excelência e grande experiência na magistratura é consequência para a indicação de juízes do STF.
Q ---> P
A sentença “A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura” pode ser corretamente representada na forma P→Q, em que P e Q sejam proposições simples convenientemente escolhidas.

Pessoal, observem que a parte em negrito não é uma CONDIÇÃO NECESSÁRIA pra que "ocorra a indicação de juízes para o STF". Neste caso é só observar o sentido da assertiva - não é por causa da palavra "consequente" que temos uma relação condicional na frase.

Pensem bem: se tivéssemos uma relação condicional estaria correta a assertiva pois fala que "P e Q são proposições convenientemente escolhidas, logo tanto faz a ordem de P e Q.

ATENÇÃO: O "e" não é conjunção, já que "grande experiência na magistratura" não possui verbo, logo não pode ser uma proposição.
Tássia Silva, concordo com vc porque, a ordem dos fatores, não altera o conteúdo, ou a idéia central.
A frase teria conectivo e valor lógico se tivesse sido construída da seguinte maneira:
"Se um currículo demonstrar excelência e grande experiência na magistratura então haverá indicação de juízes para o STF."

Aí sim ficaria P ➔ Q.
Gabarito ERRADO.

Bons estudos!
Alguem parou pra pensar que essa proposição é apenas uma proposição simples, não se trata de um "Se...Então" ?

“A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura”

O verbo "demonstre" não conta, pois está caracterizando apenas o currículo, não forma uma sentença fechada (está até no modo subjuntivo!). Não é porque tem a palavra consequência que vai ser um Se.. então..O "e" de "...e grande experiência na magistratura”, notadamente não é um conectivo lógico também, porque não liga duas sentenças fechadas.
Povo, é melhor procurar sentença do que conectivo! Se não a gente fica advinhando a questão, acertando por sorte e sorte num é pra todo dia!
Não adianta tentar acertar pelo português, pessoal!
ERRADA. É uma proposição simples, pois trata de uma única ideia.
Eu marquei errado porque pensei que há uma conjunção entre duas proposições simples. Mas com o comentário do professor e dos demais fiquei com dúvida.
Primeiramente, vamos separar as proposições, lembrando que a letra E em “...demonstre excelência e grande experiência...” não é um conectivo lógico, pois não está unindo duas proposições simples, logo:

P: indicação de juízes para o STF

Q: um currículo que demonstre excelência e grande experiência na magistratura.

Assim, para que possamos corretamente representar com uma condicional, deve-se escrever como:

Se um currículo que demonstra excelência e grande experiência na magistratura então haverá indicação de juízes para o STF.

Que ficaria Q ➔ P.

Resposta: Errado.
Representação dos conectivos:
e = ^ ;
ou = v;
se, então = -> ;
se e somente se = <->
Trata-se de uma proposição simples, com uma ideia declarativa. Portanto não pode ser uma condicional. Logo, está errada.
"Se tenho um currículo que demonstra excelência e grande experiência na magistratura, então sou indicado ao STF." Não necessariamente...
GABARITO ERRADO
Essa proposição como muitos aqui afirmaram é simples! Mas caso estivesse escrito das maneiras abaixo o gabarito seria CORRETO!

"A indicação de juízes para o STF deve ser CONDIÇÃO NECESSÁRIA para um currículo que demonstre excelência e grande experiência na magistratura."
"A indicação de juízes para o STF deve ser CONDIÇÃO SUFICIENTE para um currículo que demonstre excelência e grande experiência na magistratura."

Lembrando que tanto um quanto o outro poderá ser representado por (P --> Q), pois na questão afirma que as proposições poderão ser escolhidas convencionalmente.
quantos comentários equivocados com inúmeras curtidas.

acertou quem percebeu que não existe uma proposição composta,portanto não há p --> q (se p então q)
simples gente não tem mistério basta estudar um pouco.
Falta de atenção e raciocínio.. Li a parte "
sejam proposições simples convenientemente escolhidas" e não me toquei que não existe por ser simples P→Q.
Vamos lá!!

Galera, cuidado com os comentários inadequados. Como alguns colegas já disseram, trata-se de uma proposição simples. É só lembrar que pra CESPE, as proposições simples só tem 1 verbo. '----' Não esqueçam disso.
Obs: Se falei algo errado, me corrijam, por favor.
Verbos em orações subordinadas adjetivas restritivas (com "falsos" conectivos, como: E, OU etc.) --> NÃO CONTA COMO PROPOSIÇÃO

OBS. : SUBSTITUIR POR UM ADJETIVO E, DEPOIS, ANALISAR NORMALMENTE
GABARITO: ERRADO.
Para os não assinantes, comentário do professor a respeito dessa questão:
" Primeiramente, vamos separar as proposições, lembrando que a letra E em “...demonstre excelência e grande experiência...” não é um conectivo lógico, pois não está unindo duas proposições simples, ( isso é muito importante, vi comentários citando o E como conectivo, mas nesse caso, NÃO É) logo:

P: indicação de juízes para o STF

Q: um currículo que demonstre excelência e grande experiência na magistratura.

Assim, para que possamos corretamente representar com uma condicional, deve-se escrever como:

Se um currículo que demonstra excelência e grande experiência na magistratura então haverá indicação de juízes para o STF.

Que ficaria Q ➔ P.

Resposta: Errado. "
O comentário do professor está errado ou so eu achei isso?
Proposição simples!!!!
Não tem o que discutir.
Esse é o erro.
Proposição simples
Se um currículo demonstra excelência e grande experiência na magistratura, então haverá indicação de juízes para o STF.(conforme o enunciado, é o consequente).

Assim, a proposição:

“A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura” é indicada por Q -> P e não P -> Q.

IMPORTANTE: "que demonstre excelência e grande experiência na magistratura" o conectivo "e" não liga duas proposições. vejamos:

"...um currículo que demonstre excelência e grande experiência na magistratura"

Caso sejam isoladas as sentenças, perdem totalmente o sentido e não declaram nada objetivamente:

"...um currículo que demonstre excelência..." e "...(e demonstre) grande experiência na magistratura". Analise-as individualmente e chegarás à conclusão de que são uma só proposição.

GABARITO: ERRADO!
(Todo cuidado ainda é pouco com Raciocínio Lógico do CESPE :( )
Atenção, os trechos não são proposições, como muitos afirmam:
"A indicação de juízes para o STF". Isso é V/F? Não tem como valorar, não é proposição.
"Um currículo que demonstre excelência/" Isso é V/F? Não tem como valorar, não é proposição.
"Grande experiência na magistratura". Isso é V/F? Não tem como valorar, não é proposição.
Só nos resta então o todo:
"A indicação de juízes para o STF DEVE SER consequência de um currículo que demonstre excelência e grande experiência na magistratura" Isso é V/F? Tem como valorar, então é proposição.
Para deixar mais simples, troquem DEVE SER consequência simplesmente por "é":
"A indicação de juízes para o STF É peixada." Tá vendo que é proposição simples?
Que descaso do professor que comentou a questão...

Seria bom que todos clicassem em "não gostei" no comentário dele para ver se o site toma alguma providência.
pelo que entente não tem conectivo de condicional !!!!!
Porque não o Renato para resolução em vídeo?
Pessoa, o comentário do professor está errado! Tomem cuidado! É uma proposição simples.
Gente, embora tenha mais de um verbo, isso é uma proposição simples. Notem que não há conectivos lógicos ligando proposições.

Jesus Cristo é meu único e suficiente Senhor e Salvador !
ERRADA
A proposição é composta e condicional,onde temos uma proposição simples `´A Indicação de Juízes para o STF´´ e o antecedente é uma proposição composta: ´´currículo que demonstre excelência e grande experiência na magistratura´´.Dessa forma temos uma proposição simples e uma proposição composta.
Em qual comentário acreditar??? kkkk O professor do QC diz algo e a galera dando outras ideias.
ATENÇÃO QC...COMENTÁRIOS DOS PROFESSORES REFERENTE A RLM EM VÍDEO...EM VÍDEO...ESTAMOS PAGANDO PARA APRENDER COM AULAS TAMBÉM.
Questão interessante, errei pelo fato de pensar que este "convenientemente escolhidas" seria algo para se colocar em qualquer uma, mas pelo que vejo funciona como um "respectivamente", que bom está errando aqui, que la na prova, seja mais de boa
Concordo com Aguinaldo gasparin comentário de RLM podia ser em vídeo, fica bem mais satisfatório o aprendizado.
Meu Deus ...quem está certo..?????
vamos notificar erro pro QC, explicação total errada, realmente é uma proposição simples, tem somente uma ideia na proposição.
Esse professor mais atrapalha do que ajuda. Pronto, falei.
Pessoal, cliquem em não gostei na explicação do professor e justifiquem. Sugiro que solicitem explicações das questões de RLM em vídeo. Acabei de enviar a minha.
Galerinha, vou dar uma dica pra vcs usando o Português.
Para descobrir se a preposição é simples ou composta, primeiro devemos achar o sujeito da questão e logo em seguida ver se o predicado está falando SOMENTE deste sujeito. Vou usar a questão como exemplo....
A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura...
Sujeito: O que deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura??? A indicação de Juízes para o STF.
Predicado: O restante da frase que não contém o sujeito.... Viram que o predicado todo aponta para unicamente um único sujeito...??
Então, preposição simples....
Pessoal, primeiramente verifique se é proposição simples ou composta. Só existe uma proposição, certo?
"deve ser consequência" dá sentido a frase toda, o "e" de "excelência E grande experiência na magistratura" não é conectivo!
“A indicação de juízes para o STF" é o sujeito da oração, pode ser classificado como verdadeiro ou falso? Não!
Logo, só há uma proposição simples e não duas como induz a acertiva.
*
Bons estudos!
Pessoal, vocês estão quebrando a cabeça por besteira. O que deixaram de perceber é que o Cespe vem utilizando muito as expressões "adequadamente escolhidas" em contraposição a "convenientemente escolhidas".
Ex¹: Se João bebe muito, fica bêbado.
P: JB --> B.
Aqui a tradução lógica foi adequadamente escolhida.
Ex²: Se eu trouxer pirulito ou coxinha, ele ficará satisfeito.
P: P v C --> S
P: C v P --> S
Aqui a tradução lógica foi convenientemente escolhida, tanto faz a ordem.
Na boa, se eu me basear nas explicações do professor, estou lascado.
ERRADO!
É uma proposiçao simples e não composta como a banca introduziu na questao.
A proposição é simples. O professor botou cabelo em ovo montando uma nova proposição que não tem nada haver com a questão em comento. aqui é RLM e não reescritura de frases em português
O qconcursos poderia pagar para o guru da matemática, os vídeos dele realmente ajuda muito.
Vejam o vídeo que gravei com a resolução dessa questão

https://youtu.be/77t5d-_30H8

Professor Ivan Chagas
Um currículo demonstrar excelência e grande experiência na magistratura é condição suficiente para a indicação de juízes ao STF. (P --> Q)

A indicação de juízes para o STF é condição necessária para que um currículo demonstre excelência e grande experiência na magistratura. (Q --> P) RESPOSTA DA QUESTÃO!
que pena o QC não ter um professor bom de RLM. Ele deu duas respostas diferente para a mesma proposição. Vejam na questão Q351763 onde ele diz que essa mesma frase não caracteriza uma condiconal, e agora nesta questão ele fala que é condicional, como pode?
Segundo o professor Edgar, da Casa do Concurseiro, essa questão errada porque a proposição é SIMPLES e não composta. Não há conectivo.
é uma proposição simples, se vc pegar a frase e tentar separar em proposições elas não subsistem de maneira independente vejam:
A indicação de juízes para o STF deve ser consequência.
De um currículo que demonstre excelência e grande experiência na magistratura.??? viram?
Agora uma proposição composta de verdade:
Se amanhecer,então o sol nasce.
Amanheceu
O sol nasce.
É uma proposição simples. Não existe uma proposição composta ai.
Proposição simples, portanto sua representação simbólica é de apenas uma letra, no caso P ou Q, mas não a divisão.
ESTÃO DIZENDO QUE "A INDICAÇÃO DE JUÍZES PARA O STF" É PROPOSIÇÃO.. MAS INDICAÇÃO N É VERBO, ESTÁ ATÉ COM ARTIGO : (
Explicação da questão..

https://www.youtube.com/watch?v=77t5d-_30H8&feature=youtu.be
“A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura”

Sentença que pode ser representada por uma condicional.

A: um currículo que demonstre excelência.

B: um currículo que demonstre grande experiência na magistratura.

C: indicação de juízes para o STF.

Só ocorre C se ocorrerem A e B cumulativamente. Logo, C está condicionada a A e B.

(A ^ B) → C. Com p igual a A^B, logo proposição composta e não simples, como diz o enunciado.
não Klebert! Está proposição é simples, transmite uma só ideia, aquele e da frase não é um conectivo! Veja o video do link que a colega Leticia Rodrigues postou.

DEUS na frente sempre!!!!
Pelo contrário, a resposta é Q→P !!!

P = A indicação de juízes

Q=Curriculum demonstre eficiência....
Prof. Ivan Chagas, VLW!
Quando a setença possuir mais de um verbo, aqueles que forem precedidos dos termos ´`para`` e ``que´, não trarão novas informações e sim servirão para complementar a primeira informação e com isso a proposição, apesar de possuir mais do que um verbo, ainda assim será chamada simples

Créditos: Jhoni Zini Focus concursos
Eu acertei, mas vou de encontro a tudo que foi dito aqui. Eu intepreto da seguinte forma:

P: A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência

Q: A indicação de juízes para o STF deve ser consequência de um currículo que demonstre grande experiência na magistratura

P^Q . É uma proposição composta com o conectivo 'e'.
Segunda vez ...o cespe cobrou esse mesmo assunto no ano de 2015: A é consequência de B. Vou te fazer uma pergunta bem boba...

Tem sentido de condição : vc me diz sim.

Tem conctivo : vc me diz NÃO.

Ahhhh Eliel, mas não tem aqueles casos do "Mas" servir como "E",tipo :

Eliel estudou muito, mas não passou ( sentido de ''E")

Gente, isso é um caso a parte...já pacificado pelo cespe. Agora dizer que "em consequencia", "condição necessária" funciona como "Se, então´" é forçar a barra.

GABARITO "ERRADO"
Pessoal estou notando muitos comentários divergntes sobre essa questão. De acordo com o comentário do professor na frase existem apenas 2 preposições. De fato já ouvi em outros sites que você descobre o número de preposições de acordo com o número de verbos, então vamos contar os verbos :

INDICAÇÃO,DEVE,SER,DEMONSTRE >

Mas observe que não existem 4 proposições na frase, isso se deve ao fato do conjunto de palavras "deve ser consequencia" representar o conectivo (--->)

Então fica assim :

P: indicação de juízes para o STF

"DEVE SER CONSEQUÊNCIA" (---> )

Q: um currículo que demonstre excelência e grande experiência na magistratura.

P --> Q é a resposta certa. E não.. Q--> P

Mas já resolvi uma questão em que a locução " È consequência de " não foi considerada como o conectivo (--->). Realmente ainda não consegui entender por quê.
PESSOAL, CUIDADO!

Dizer que:

"P: indicação de juízes para o STF "DEVE SER CONSEQUÊNCIA" (---> )
Q: um currículo que demonstre excelência e grande experiência na magistratura. P --> Q é a resposta certa. E não.. Q--> P"

Está errado!

A questão diz: "...em que P e Q sejam proposições simples convenientemente escolhidas". Ou seja, você pode escolhe seus valores. Então eles também podem ser:

P: um currículo que demonstre excelência e grande experiência na magistratura.

Q: A indicação de juízes para o STF.

Então, "Q --> P" também estaria certo. O que faria o gabarito ser CERTO, já que você pode escolher quem é P, e quem é Q.

O que torna o gabarito ERRADO é o fato de ser uma única proposição simples.

EXPLICAÇÃO:

Indicação, deve e demonstre não estão exercendo funções de verbo.

INDICAÇÃO: tem um artigo " A indicação", isso faz com que ele não tenha papel de verbo.

DEVE: apenas é verbo auxiliar do verbo SER.

DEMONSTRE: sentido imperativo, perdendo valor na proposição.

Então, apenas SER, de fato, está com a função de verbo.

Mas o que mais indica que é uma única proposição simples: é que no "Se... então", independente como ele apareça (também pode aparecer como "É consequência de"), tem que usar vírgula para separar as duas proposições.

E nota-se que a sentença não possui vírgulas.

Portanto trata-se de UMA ÚNICA PROPOSIÇÃO SIMPLES.

Lembrando: aplicando o raciocínio sugerido no início desta explicação, você vai acerta por conhecidência. Se aplicá-lo em outra questão similar, provavelemente irá errar. CUIDADO!

Gabarito: ERRADO.
O cara tem PHD e dá uma mancada dessa.

Isso nunca foi, não é e nunca será uma proposição composta pra CESP.
Está errada pq é uma proposição simples. Só pode ser representada por uma letra.

Cliquem no comentário do professor e em "não gostei" e escrevam sua justificativa. Na explicação, ele só inverteu as letras sendo que a questão deixa claro que P e Q são proposições convenientemente "escolhidas". Ou seja, você pode escolher a letra que for conveniente para se referir a proposição. Inverter a ordem das letras não mudaria o gabarito. O CESPE escolheu o que lhe foi conveniente. Dizer que o correto é Q-->P é um equívoco. Então esse não pode ser o erro da questão. Está errada pq é uma proposição simples.

Leiam o comentário do Marcelo Neves. Ele está certo.
Pessoal, conforme comentário do professor no vídeo: https://youtu.be/77t5d-_30H8

Toda esta ideia é uma única proposição, portanto é representada somente por P
Errada
Isso não é uma proposição simples, "é uma consequência de" pode ser lido como um "Se...Então...". O erro na questão está na "condição suficiente" e "condição necessária".
Na explicação do professor do Qconcursos, ele diz que o erro está em ser P--->Q ao invés de Q-->P. No entanto, a questão fala pra escolher as proposições de forma conveniente, daí tanto faz quem eu chamo de P ou Q. Baseando na explicação dele, estaria certa sim.
Inadmissível o professor explicar a questão de forma errada. Onde está o QConcursos que não viu isso? Absurdo!!!!
Errada.

É uma proposição simples.

*O comentário do professor está sofrível.¬¬'
kkkkkkkkk ! O professor comentarista caiu na pegadinha do cespe !! Tá dureza esse a banca ! Vou virar astronauta da NASA de tanto estudar RL desta banca !! kkkkkkk
aprendi que essa palavra consequência não gera condicional,

gabarito ERRADO.
Se tivesse dois verbos no infinitivo antes E depois do "é consequencia para" seria aceito como proposições compostas.

Ex: A indicação de juízes para o STF deve ser (até aqui tudo certo) consequência de um currículo que demonstre (verbos após que e para não vale) excelência e grande experiência na magistratura

Lembrando pessoal, verbos depois de "que" e "para" não contam como verbo para se caracterizar uma proposição simples.

Agora segue um exemplo que daria certo neste caso:

A indicação de juízes para o STF deve ser consequência de um se ter um currículo que demonstre excelência e grande experiência na magistratura

a -> A indicação de juízes para o STF deve ser

b-> se ter um currículo que demonstre excelência e grande experiência na magistratura

b -> a

Lê-se ao contrário.

ter um currículo que demonstre excelência e grande experiência na magistratura É CONDIÇÃO NECESSÁRIA PARA A indicação de juízes para o STF

Ao mesmo modo que:

A indicação de juízes para o STF É CONDIÇÃO SUFICIENTE PARA ter um currículo que demonstre excelência e grande experiência na magistratura

Espero ter ajudado vocês.

FOCO E FORÇA!!!
Oia o professor comendo banana de novo.

Não dá pra enxergar proposição composta aí nunca.
Pessoal, não basta reclamar do professor aqui. De fato ele é ruim explicando as questões, apesar do currículo. Não basta ter currículo para ser um bom professor. Ele tem pouca habilidade para explicar alguma coisa, cai nas pegadinhas da banca, explica a questão em cima do gabarito, carece de didática... enfim. Assinantes, deixem o seu 'NÃO GOSTEI' no comentário do professor e esperemos que o QC melhore isso
a questão fala em duas proposicões simples, a primeira está correta, mas a segunda não pode ser proposição simples, pois não possui verbo.
P: A indicação de juízes para o STF deve ser consequência de um currículo de demonstre excelência

e

Q: A indicação de juízes para o STF deve ser consequência de um currículo que demonstre grande experiência na magistratura

P ^ Q

Não pode ser representada por uma proposição do tipo P---->Q, pois se trata de uma conjunção P ^ Q

Gabarito: errado

Se eu estiver errado, pesso desculpas!
sempre q aparecer o termo ( CONSEQUÊNCIA ) e antes e depois estiver um verbo no infinitivo - terminação ar, er, ir - vai ser SE..., ENTÃO. Sendo q a questao acima tem apenas um verbo no infinitivo. ( QUESTÃO - ERRADA )

bons estudos a todos. !
Contribuindo e reiterando o que disseram: o comentário da Tássia Silva é o mais correto e coerente.

Questão Errada
Resumindo pra todo mundo Cespe considerou como preposição simples ! LOGO APÉNAS UMA UNICA IDEIA

Poderia ser representado por P e não por P---->Q,
Pessoal cuidado com alguns comentários, essa assertiva é uma proposição simples, esse " e" na questão não é um conectivo. vi em alguns comentários o pessoal confundindo , afirmando até ser condicional.
Primeiramente, vamos separar as proposições, lembrando que a letra E em “...demonstre excelência e grande experiência...” não é um conectivo lógico, pois não está unindo duas proposições simples, logo:

P: indicação de juízes para o STF

Q: um currículo que demonstre excelência e grande experiência na magistratura.

Assim, para que possamos corretamente representar com uma condicional, deve-se escrever como:

Se um currículo que demonstra excelência e grande experiência na magistratura então haverá indicação de juízes para o STF.

Que ficaria Q ➔ P.
P: indicação de juízes para o STF

Q: um currículo que demonstre excelência e grande experiência na magistratura.

Resposta: Q ---> P
“A indicação de juízes para o STF deve ser consequência de um currículo que demonstre excelência e grande experiência na magistratura”

"consequência de" só sera condicional (P>Q) quando houver um verbo antes e outro depois.

Na questao temos uma proposiçao simples, visto que as particulas "PARA" e "QUE" anulam o verbo a sua frente.

“A indicação de juízes para o STF deve ser consequência de um currículo QUE demonstre excelência e grande experiência na magistratura”
DEMONSTRE excelência e grane experiência.

Temos um único sentido trazido pelo verbo demonstrar. Portanto, trata-se de uma proposição simples.
É proposição simples:

Observem:
https://youtu.be/77t5d-_30H8
Errado, a indicacao trata do SE ENTAO
Toda proposição só tem uma ideia, por isso é simples. O ''e'' apenas enumera qualidade, não é conectivo.

ID

1074928

Banca

CESPE / CEBRASPE

Órgão

Petrobras

Ano

2007

Provas

CESPE - 2007 - Petrobras - Analista de Comércio e Suprimentos Júnior

Disciplina

Raciocínio Lógico

Assuntos

Julgue os itens que se seguem.

Considere as proposições abaixo: p: 4 é um número par; q: A PETROBRAS é a maior exportadora de café do Brasil. Nesse caso, é possível concluir que a proposição p V q é verdadeira.

Alternativas

Certo

Errado

Comentários

Gabarito certo.
OBS 1: No conectivo “ou” (v) a proposição Composta A v B só será F, quando A e B forem ambas F, caso contrário será V.
OBS 2: Pelo menos um for V, a proposição composta A v B será V
EXEMPLO:
R: Brasília é a capital do Brasil
S: São Paulo é a capital da Argentina.
A: Brasília é a capital do Brasil ou São Paulo é a capital da Argentina.
V A: R V S
V F
Separando as proposições:

p: 4 é um número par.

q: A PETROBRAS é a maior exportadora de café do Brasil.

Tomando a proposição “p" como verdadeira e “q" como falsa, pois sabemos que 4 é realmente um número par e que a Petrobrás não exporta café, temos:

p v q = V v F

E pela tabela – verdade da disjunção, V v F = V, logo é possível concluir que a proposição p V q é verdadeira.

Resposta: Certo
Certo.

Disjunção Inclusiva.....se tem um V o resto tudo é "V"
GABARITO: CERTO

Na Disjunção Inclusiva (ou) só será falso (F) se ambas forem falsas(F).

DISJUNÇÃO
p q p ∨ q
V V V
V F V
F V V
F F F
Ainda que eu saiba que 4 é par, a questão não deve valorar para concluirmos algo do tipo? Até porque, se fosse o caso de colocar duas empresas desconhecidas, por exemplo, não teria como eu concluir algo sem ter algum valor.
Propriedade de dominação.
V ou Q = V
No OU só é F se todas proposições forem F.
O SUJEITO Q LER O COMANDO DA QUESTAO RÁPIDO

E NAO PERCEBE O CONECTIVO ou ERRA FÁCIL FÁCIL.
Essa questão perde quase toda a lógico de proposições, em todas as aulas que eu estudei sempre foi falado que não necessariamente aquilo que é verdade na vida real será realmente verdade das questões de RLM ao menos que os valores lógicos sejam dados ou que a questão faça com que você aprecie valores para as proposições. Nessa questão dá margem para você pensar que NECESSARIAMENTE o 4 em TODAS as proposições seria validado como verdadeiro o que de fato não é verdade. Mas... em todo caso mesmo não concordando com a interpretação da banca era só saber que o conectivo V , só será falso se ambos forem falsos.
p é V e o q (?) por mais que não de para concluir que é V ou F, como a questão trata de disjunção inclusiva (OU), será Verdadeira de qualquer forma, pois o "OU" só é F quando for TUDO F (F=F).

p v q:

V v F: V
V v V: V.
Confundi o uso dos conectivos e me lasquei. Vou ali me deitar na BR.
CERTO

Questão um pouco subjetiva, mas não podemos dar mole na prova.

P: 4 é um número par (posso afirmar se é verdadeiro ? SIM, POIS 4 É PAR)
Q: A PETROBRAS é a maior exportadora de café do Brasil. (posso afirmar ? NÃO, pode ser F ou V).

Porém sabemos que na conexão OU / V só é FALSO se as TODAS forem falsas.

Logo: V v F/V = V
Se atentar para o comando da questão!

É possível? SIM!

V ou V
V ou F
F ou V

ID

1085719

Banca

FCC

Órgão

METRÔ-SP

Ano

2010

Provas

FCC - 2010 - METRÔ-SP - Supervisor de Linha Operacional

Disciplina

Raciocínio Lógico

Assuntos

A negação da proposição “Existem Linhas do Metrô de São Paulo que são ociosas.” é:

Alternativas

Nenhuma Linha do Metrô de São Paulo é ociosa.

Nenhuma Linha ociosa é do Metrô de São Paulo.

Nem toda Linha do Metrô de São Paulo é ociosa.

Algumas Linhas do Metrô de São Paulo não são ociosas.

Toda Linha do Metrô de São Paulo é não ociosa.

Comentários

Para encontrar a negação desta proposição, use o seguinte "macete":

1° imagine que alguém te fez a afirmação: “Existem Linhas do Metrô de São Paulo que são ociosas.”

2° imagine o que é o MÍNIMO que você precisaria fazer para provar que o autor da frase mentiu para você.

Portanto, admitindo que alguém te fez a afirmação, o que é o mínimo que você precisa fazer para provar que isto é mentira? Você precisa analisar TODOS as linhas do metrô de São Paulo para verificar que nenhuma delas é ociosa e então dizer que "Nenhuma linha é ociosa"? Ou basta que você encontre UMA linha que não seja ociosa para demonstrar que a afirmação é mentirosa? Neste caso, basta encontrar uma linha que não seja ociosa. Por isto, a negação é dada pela frase:

Algumas Linhas do Metrô de São Paulo não são ociosas. Gabarito Letra D

Fonte do embasamento, Professor Arthur Lima
Link: https://www.estrategiaconcursos.com.br/blog/raciocinio-logico-negacao-de-todo-e-nenhum-4/

Bons estudos!
Achei o gabarito muito estranho. Para a expressão “Existem Linhas do Metrô de São Paulo que são ociosas”, entendo o seguinte: “Existem Linhas do Metrô de São Paulo que são ociosas E OUTRAS QUE NÃO SÃO OCIOSAS”. Essa segunda parte é equivalente ao gabarito “Algumas Linhas do Metrô de São Paulo não são ociosas” e não está contrariando (negando) a proposição do enunciado. Alguém consegue me explicar?
GAB: D

Repare que eu poderia dizer essa mesma frase da seguinte forma:

Algumas linhas do Metrô de São Paulo são ociosas

Concorda que não há diferença alguma, mas por quê?

O que ocorre é frequente confunde-se com a frase no singular:

Alguma Linha do Metrô de São Paulo é ociosa.

Repare que esta frase podemos ter 1 ou mais linhas do metrô de São Paulo ociosa. Ao passo que quando a frase está no plural, ou seja, temos mais 1 linha do metrô de São Paulo ociosa.

E qual a diferença na negação?

É porque no singular, a negação corresponde a “nenhum” e no singular podemos dizer “alguns”

Ou seja:

~( Algumas linhas do Metrô de São Paulo são ociosas) = Algumas linhas do Metrô de São Paulo não são ociosas

E

~( Alguma linha do Metrô de São Paulo é ociosa) = nenhuma linha do Metrô de São Paulo é ociosa.

Estratégia Concursos.
Estranho. Fui na E porque simplesmente estudei assim. Negação de todas são = alguma não é. E vice-versa.
Acho que essas questões antigas não são mais vigentes atualmente.
Vou compartilhar a minha linha de raciocínio:

Para resolver essa questão lembrei de um MACETE, vejam:

Quando quiser a negação, nela deverá aparecer o PEA:

P > Pelo menos um...+ não
E > Existe um... + não
A > Algum(as)... + não

A Letra D trás: Algumas Linhas do Metrô de São Paulo não são ociosas.
Acabei de checar o gabarito oficial do Metro 2010 - Supervisor de Linha Operacional através do site PCI CONCURSOS e o gabarito é a letra (E). Ufa! Esteva quase tendo um troço de tão contrariado e inconformado.
Essa foi pra não zerar. #moleza
A negação da proposição “Existem Linhas do Metrô de São Paulo que são ociosas" pode ser feita de duas formas:

1) Utilizando-se o TODO (e discordando do verbo):

Toda Linha do Metrô de São Paulo é não ociosa. (Letra E)

OU

2) Utilizando-se o NENHUM (e concordando com o verbo):

Nenhuma Linha do Metrô de São Paulo é ociosa. (Letra A)

Dessa forma, essa questão deveria ter sido anulada. Valeu! Espero ter ajudado!

ID

1087159

Banca

COPEVE-UFAL

Órgão

IF-AL

Ano

2011

Provas

COPEVE-UFAL - 2011 - IF-AL - Técnico em Contabilidade

Disciplina

Raciocínio Lógico

Assuntos

Admita verdadeira a declaração: “se gato é felino, então cachorro não é felino”. Nestas condições, concluímos corretamente que,

Alternativas

se gato não é felino, então cachorro é felino.

se cachorro é felino, então gato é felino.

se cachorro é felino, então gato não é felino.

se cachorro não é felino, então gato não é felino.

se cachorro não é felino, então gato é felino.

Comentários

A -- > B = ~ B -- > ~ A

gato --> ~ cachorro = cachorro --> ~ gato

Regra do "inverte-se e troca."
c) se cachorro é felino, então gato não é felino.

Equivalência da Condicional

P -> Q = ~Q -> ~P

“se gato é felino, então cachorro não é felino”

G ~C

G -> ~C ===>> "volta negando" C -> ~G
Famoso NEGA e INVERTE
Poxa, só acertei porque fiz a tabela da verdade!!!

Letra: C

"Força, pois chegaremos lá"

ID

1090024

Banca

FGV

Órgão

CODESP-SP

Ano

2010

Provas

FGV - 2010 - CODESP-SP - Guarda Portuário

Disciplina

Raciocínio Lógico

Assuntos

Considere a afirmação: “Todo gato preto é manso.

Com base nessa afirmação, pode-se concluir que

Alternativas

todo gato manso é preto.

todo gato branco não é manso.

todo gato que não é preto não é manso.

todo gato que não é manso não é preto.

existem gatos que não são mansos e são pretos.

Comentários

Letra D. Se o gato não é manso, não pode ser preto. A única que podemos dar 100% de verdade com base na afirmação.
a), b), c) Pode ou não ser verdade
e) Não pode ser verdade
Recomendo separar as coisas:

- GATOS PRETOS

- MANSOS

colocar no grafico... TODO gato preto é MANSO. o conjunto GATO PRETO tá dentro do conjunto MANSO. ai faça os testes dos itens.

a) todo gato manso é preto. NÃO NECESSARIAMENTE, VISTO QUE O CONJUNTO MANSO É O MAIOR

b) todo gato branco não é manso. NÃO TEM NEM GATO BRANCO NA PARADA rsrs

c) todo gato que não é preto não é manso. NADA, PODE SER QUE TENHA SIM.

d) todo gato que não é manso não é preto. GABARITO

e) existem gatos que não são mansos e são pretos. NÃO, PRA SER PRETO TEM QUE SER MANSO PRIMEIRO.

GABARITO 'D'
Recomendo decorar a tabela de equivalências:

Se...,então... ----> ~q ---> ~p

Logo: todo gato que não é manso não é preto.
Algum professor do Qconcursos pra explicar essa questão. Sinceramente não conseguir engoli-la! Grato!
Ser manso é condição necessária para ser preto. Logo, se não for manso não pode ser gato preto.
Nesse caso não utilizaremos TODO, ALGUM E NENHUM

São apenas conectivos:

SE TODO GATO É PRETO ENTÃO É MANSO

EQUIVALÊNCIA

P->Q = ~Q -> ~P

SE TODO GATO QUE NÃO É MANSO ENTÃO NÃO É PRETO

d) todo gato que não é manso não é preto.
Errei por não ler o enunciado, logo corri na negação , que seria a letra E, só depois que percebi o equivoco.
Também não consegui entender a lógica.
LETRA D
GAB. D

Se na questão tem, TODO, ALGUM, NENHUM ; mais fácil ir para os desenho dos conjuntos.

(((((((G. MANSO(G. PRETO ) G. MANSO)))

ORA, se todo gato que não é manso não é preto.= pq, o conjunto do G.PRETO está dentro do gato manso.
Letra D

Você pode fazer os conjuntos se quiser, mas eu recomendo que você entenda o seguinte raciocínio.

Todo A é B = Todo não B é não A.

É o mesmo esquema da equivalência da condicional(Se A então B = Se não B então não A[nega e inverte a ordem]).

Todo gato preto é manso = Todo gato não manso é gato não preto(nega e inverte a ordem).

D)Todo gato que não é manso não é preto(Só foi escrita de uma maneira diferente).

Você quer saber o porquê de tudo isso? Por que você pode fazer uma equivalência do "Todo" usando a mesma fórmula da condicional(nega e inverte a ordem)?

Simples, por que elas são equivalentes.

Todo A é B = Se A então B.

Logo:

Fazer a equivalência de "Se A então B" negando e invertendo a ordem, é a mesma coisa que negar e inverter a ordem do "Todo".

Cansado de ficar tentando decorar prazos de lei, teclas de atalho ou classificações de doutrinadores usando mnemônicos malucos que apenas quem os inventou entende?

Use Anki, um programa de flashcards totalmente gratuito e open-source (Código Aberto), disponível para Windows, Mac, Linux, iOS e Android.

https://apps.ankiweb.net/

ID

1090324

Banca

VUNESP

Órgão

PC-SP

Ano

2014

Provas

VUNESP - 2014 - PC-SP - Escrivão de Polícia Civil

Disciplina

Raciocínio Lógico

Assuntos

A implicação é um tipo de relação condicional que pode ocorrer entre duas proposições e desempenha um importante papel nas inferências em geral. Esta relação é adequadamente descrita por meio da expressão

Alternativas

“Isto ou aquilo”

“Isto e aquilo”

“Não isto ou não aquilo”

“Se isto então aquilo”.

“Nem isto e nem aquilo”.

Comentários

Na lógica e na matemática a implicação, ou condicional é a indicação do tipo "SE...ENTÃO", indicando que uma condição deve ser satisfeita necessariamente para que a outra seja verdadeira.
Ex.: "Se P então Q"; "Se eu estudo, então eu passo no concurso"; etc
Explicitando as alternativas: a) “Isto ou aquilo” - proposição disjuntiva (conectivo "ou") b) “Isto e aquilo” - proposição conjuntiva (conectivo "e") c) “Não isto ou não aquilo” - proposição disjuntiva (conectivo "ou") d) “Se isto então aquilo”. - proposição condicional (conectivo "se... então") e) “Nem isto e nem aquilo”. - proposição conjuntiva (conectivo "e) Há ainda a proposição disjuntiva exclusiva, representado pelo conectivo "ou.... ou" (ex: ou isto ou aquilo) E também a proposição bicondicional, representado pelo conectivo "se somente se" (ex: se isto somente se aquilo / isto se somente se aquilo). Como o enunciado pede a condicional, resposta D
O enunciado da questão te dá a resposta quando diz: "A implicação é um tipo de relação condicional..."

Condicional = "SE...ENTÃO" (-->)

A resposta muitas vezes está no anunciado.

Bons estudos!
mata a questão só de vc saber que implicação/condicional é o mesmo que ---> se .... então
Saudade dessas perguntas que nunca mais irão cair
“Isto ou aquilo” DISJUNÇÃO ( v )

“Isto e aquilo” CONJUNÇÃO ( ^ )

“Não isto ou não aquilo” NEGAÇÃO DA CONJUNÇÃO ~( ^ )

“Se isto então aquilo”. CONDICIONAL ( ---> )

“Nem isto e nem aquilo”. NEGAÇÃO DA DISJUNÇÃO ~( ^ )
saudade das provas de antigamente que eu nao fiz
@andreffontanela
gab-d

“Se isto então aquilo”.
MAIS FÁCIL QUE ESSA SÓ SE PONTUAREM PARA ESCREVEREM O NOME NA PROVA

ID

1105987

Banca

CESPE / CEBRASPE

Órgão

CADE

Ano

2014

Provas

CESPE - 2014 - CADE - Nível Médio - Conhecimentos Básicos

Disciplina

Raciocínio Lógico

Assuntos

Considerando os conectivos lógicos usuais e que as letras maiúsculas representem proposições lógicas simples, julgue o item seguinte acerca da lógica proposicional.

A sentença “Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais” é uma proposição lógica composta.

Alternativas

Certo

Errado

Comentários

Pessoal!
Tenho verificado que a CESPE tem considerado como cada preposição como sendo uma oração, então para ser uma oração tem que ter verbo, conforme a questão acima só tem um verbo, logo será uma proposição simples.

Bons estudos!
Sucesso a todos!
Proposição simples; pode ter um sujeito ou mais, contudo, apenas uma única ação referente a ele(s):
Proposição compostas; podem ter um único sujeito ou mais, contudo, deve possuir mais de uma ação referente a ele(s).
Bons estudo a todos... FFF!
- Os candidatos que estão somente na condição de aprovados não estarão submetidos ao Regime .....

- Os candidatos aprovados e nomeados, sim, estarão submetidos ao Regime ....
logo, não pode separar em duas proposições. PROPOSIÇÃO SIMPLES.
Muito bem observado o comentário apresentado pelo Wilham
Faltou um conectivo na questão. Isto é, o "e" que apareça nela, é uma conjunção aditiva. Cespe e seus venenos.
Eu julguei da seguinte forma:

Se os candidatos forem aprovados e nomeados então estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais.

Não está certo??? O conectivo está subentendido....
devemos observar na proposição se há uma oração completa,pois se faltado o verbo não é proposição.
Os sujeitos " candidatos aprovados e nomeados ( sujeito )" tem uma única ação que é a de estarem subordinados ao regime jurídico ...
Proposição simples - são declarações afirmativas ou negativas, composta por UM SUJEITO e UM PREDICADO, que podem ser (V) ou (F); já as proposição composta - é toda frase declarativa, afirmativa ou negativa, formada pela ligação da duas ou mais proposições simples através dos operadores lógicos. (e; ou; ou...ou; Se...,então; Se e somente se).
Sujeito: é o termo da oração que funciona como suporte de uma afirmação feita através do predicado.

Predicado: é o termo da oração que, através de um verbo, projeta alguma afirmação sobre o sujeito.
Sendo assim, verifica-se que o SUJEITO na frase são “Os candidatos aprovados e nomeados", o restante é PREDICADO., logo PROPOSIÇÃO SIMPLES.
A sentença “Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais” não é uma proposição lógica composta, pois a mesma possui apenas um verbo, “estarão”.

Obs: Proposição simples: é toda sentença fechada declarativa que exprime um pensamento que pode ser verdadeiro ou falso – Ex: Maradona é Argentino.

Proposição composta: é aquela formada por duas ou mais proposições simples (mínimo de 2 verbos). Não se deve confundir com sujeito composto.

Resposta : ERRADO.
Excelente explicação Adriano Pereira !!
Complementando a explanação do Adriano, pode-se deduzir que havendo apenas um verbo na proposição, logo não poderia haver mais de um sujeito, portanto a Proposição é Simples.
Resposta :ERRADA
Proposição simples: A frase inteira , sem conjunção, que sejam declarativas,afirmativa ou negativa. Podendo ser negativas ou positivas
Essa questão é lógica. O candidato aprovado e nomeado é uma mesma pessoa. logo, verifica-se que só tem uma sujeito. Agora, se fosse OS CANDIDATOS APROVADOS E REPROVADOS não teria como ser a mesma pessoa.
Trata-se de questão plenamente discutível!

Embora não possamos fragmentar o sujeito: "candidatos aprovados e nomeados", podemos fragmentar a subordinação ao:
1) Regime Jurídico dos Servidores Civis da União;
2) Das Autarquias
3) Das Fundações Públicas Federais

Sim. São três proposições simples que o CESPE considera como apenas uma. Nos seus concursos, melhor seguir esse posicionamento.
Uma proposição precisar ter:
-VERBO
-SENTIDO
-SUJEITO.

como só temos um verbo, caracteriza-se uma proposição simples.
Proposição simples - são declarações afirmativas ou negativas, composta por UM SUJEITO e UM PREDICADO, que podem ser (V) ou (F); já as proposição composta - é toda frase declarativa, afirmativa ou negativa, formada pela ligação da duas ou mais proposições simples através dos operadores lógicos. (e; ou; ou...ou; Se...,então; Se e somente se).
Sujeito: é o termo da oração que funciona como suporte de uma afirmação feita através do predicado.

Predicado: é o termo da oração que, através de um verbo, projeta alguma afirmação sobre o sujeito.
Sendo assim, verifica-se que o SUJEITO na frase são “Os candidatos aprovados e nomeados", o restante é PREDICADO., logo PROPOSIÇÃO SIMPLES.
não há conectivo, logo é uma preposição simples.
Não há conectivo, pois o "e" apenas liga os "aprovados" aos "nomeados"! Se tentarmos separar não teria nenhum sentido, ficaria incompleta!
ERRADA
O raciocínio é que dentro dessa sentença eu não consigo tirar outra que tenha sentido completo.
Errado.
Lembrando que:
Para o cespe:
proposição simples = 1 verbo apenas.
proposição composta = mais de 1 verbo.
Para outras bancas:
proposição simples = sem conectivo.
proposição composta = com conectivo.
Concordo com a maioria dos comentários. Entretanto fato é que 'todo nomeado é um aprovado' 'mas nem todo aprovado é um nomeado', e isto, é algo que poderia ser discutido em uma condição lógica. Dessa forma 'ser aprovado' e 'ser nomeado' são condições que precisariam ser satisfeitas positivamente. Mas 'Se a prova foi feita pelo Cespe, então é melhor não discutir'.
Valeu pela dica Carol não sabia disso sobre o Cesp. Acertei a questão usado o seguinte raciocínio:
"Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais".
Sentença de sentido completo com verbo e sem conectivo que expressa claramente apenas um ideia.
Outra maneira de responder a questão é perceber que, em começo de frases onde se tem por exemplo: "Dyego e Maria são instrutores de um órgão público" o Cespe sempre considera o vocábulo "são" como proposição simples. No caso da questão: Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais, com base no exemplo que mencionei, é uma proposição simples.
Item errado.
Esse negócio de verbo não dá certo, olha essa questão:
CESPE: Julgue o item que se segue, relacionado à lógica proposicional.

A sentença “O sistema judiciário igualitário e imparcial promove o amplo direito de defesa do réu ao mesmo tempo que assegura uma atuação investigativa completa por parte da promotoria” é uma proposição lógica composta.
Resposta: errado.

Acredito mais na teoria da Kallyne Cabral.

1 sujeito: proposição simples

Mais de 1 sujeito: composta.
Muito bom o comentário do Adriano Pereira: simples e direto!

Parabéns! Bons estudos!
a proposição só expressa uma ideia, portanto é simples.
GAB. ERRADO
Para i Cespe: dois sujeitos e um predicado, ela considera proposição lógica simples.
"Bruno Villar" Cers
Alguns comentarios dizem respeito aos verbos. Mas essa sentenca contem dois verbos e nao apenas um. (aprovados e nomeados).
Aprovados e Nomeados é verbo???????
Acho que o único verbo que tem nessa frase é "Estarão" se eu estiver errada, só avisar ;)
Errado.

Cuidado com esse tipo de questão, uma proposição é simples quando declara uma única coisa sobre um único objeto, então observar apenas a quantidade de verbos não é suficiente para diferenciar uma proposição composta de uma proposição simples, a exemplo do que o Cespe colocou no TRT17 em 2009:
“O juiz determinou a libertação de um estelionatário e de um ladrão” (J age sobre E e L)
Essa proposição tem apenas um sujeito, um verbo, um objeto porém dois complementos nominais (um estelionatário e um ladrão), podendo ser reescrita como
“O juiz determinou a libertação de um estelionatário E o juiz determinou a libertação de um ladrão” (J age sobre E e J age sobre L), quer dizer, o juiz determinou duas coisas diferentes.

Logo, a proposição “Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais” é simples porque declara apenas uma coisa (estarão subordinados ao RJU) sobre um único objeto (os candidatos).
Tenho essa e outras questões, além de aulas teóricas, resolvidas em vídeo. Acesse http://www.tutorraciociniologico.com.br/
Esse negócio de pra uma banca ser uma coisa e para outra ser algo diferente é uma babaquice. Em raciocínio lógico sempre aprendi que o que determina se uma sentença é composta ou simples, é a presença ou não de conectivos.
Só um desabafo!!
E o conectivo "e" (aprovados e nomeados), não conta? Os candidatos poderiam ser aprovados e não nomeados...

Isso é bastante complicado!
proposição simples... para ser composta é necessário pelo menos dois verbos, e na questão só tem um que é ESTARÃO
vacilei porque não atentei para isso.
Eu entendi que a letra O representa os candidatos aprovados e nomeados e as outras letras maiúsculas representam o regime jurídico único e etc etc etc , mas estar subordinadas não quer dizer condição sufciente.Certo Ronilton Loyola????#RoniltonLoyola
Vejam o vídeo que gravei com a resolução dessa questão:
https://youtu.be/kV5O2Y-kSJ8
Professor Ivan Chagas
Muito bom o vídeo!!!
simples tem só um verbo!!!
Temos que apenas entender como a CESPE funciona, ou seja, quando se declara + de uma coisa sobre 1 objeto = Prop. Composta e quando se declara uma coisa sobre 2 objetos temos então Prop. Simples.
Ex.:
* Joana estuda inglês e canta (P. Composta).
* Joana e Cláudia são cantoras (P. Simples)
Pessoal com a Cespe não vão nessa idéia de que tendo mais de um verbo é composta, pois já vi nesse site casos de ter mais de um verbo e ser simples, o que a Cespe cobra é a idéia que está passando ou a mensagem que passa se é apenas uma.
Bons estudos!!
Candidatos não tem uma forma de lógica apenas para o CESPE. Tem que aprender a interpretar o pedido na questão.
A questão está errada porque o "e" na expressão "Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais" não pode ser um conectivo de conjunção pois não está ligando duas ideias apenas somando que os candidatos subordinados serão além dos aprovados, também os nomeados. É uma condição de que para estar no Regime Jurídico precisa ser aprovado e nomeado. Ambos.
A questão estaria correta se fosse:
"Os candidatos aprovados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União e os nomeados das Autarquias e das Fundações Públicas Federais." (o candidato aprovado está subordinado ao regime da União, já os nomeados ao regime das Autarquias e Fundações - duas ideias distintas)
ou ainda,
"Os candidatos aprovados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e os nomeados das Fundações Públicas Federais." (o candidato aprovado está subordinado ao regime da União e das Autarquias, já os nomeados ao regime das Fundações - duas ideias distintas)
corretissimo seu comentario !!
Questão fácil....

espero uma dessa no dia da prova !!
O que se tem é sujeito composto através de uma proposiçao simples.
DIABO KKK
Proposição simples, pois só apresenta uma ideia. O sujeito composto no inicío não representa duas proposições.

Errada
Proposição Simples = apresenta uma ideia

A questão fala do que? dos candidatos, logo, uma ideia
É uma proposição simples, um só pensamento, a ideia da proposição gira em torno dos candidatos aprovados.
Conjunção "e" na questão apenas exerce a função de listagem e não de unir de ideias distintas
Não consigo entender, essa questão deu certa: A proposição “Quando um indivíduo consome álcool ou tabaco em excesso ao longo da vida, sua probabilidade de infarto do miocárdio aumenta em 40%” pode ser corretamente escrita na forma (P∨Q) --> R, em que P, Q e R sejam proposições convenientemente escolhidas.
ver https://youtu.be/kV5O2Y-kSJ8 + comentário de milena bobre
QUESTAO CORRETA

POIS OS CONCTIVOS NESSA QUESTAO DAO UMA IDEIA DE SOMA,FICANDO PROPISIÇAO SIMPLES
GABARITO: ERRADO
Os candidatos aprovados e nomeados (sujeito composto) estarão subordinados (locução) o resto é complemento.

Note que só tem um verbo (locução), para que seja composta, necessitaria, no mínimo, dois verbos.
Olá pessoal,

Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/bDwlrOv0bsA

Professor Ivan Chagas
www.gurudamatematica.com.br
so um verbo = proposição simples - dois verbos proposição composta #rumo a pmce @marquinho
Errado.
Toda a frase disposta pela banca possui apenas uma ideia central, que está ligada a “Os candidatos”; logo, trata-se de uma proposição simples.

Questão comentada pelo Prof. Márcio Flávio
Nas questões do CESPE não se apeguem ao sujeito ou verbo da oração, mas sim à IDEIA da oração
Questão da PF - 2018 | Prova para agente | - Anulação por divergência doutrinária no que tange ao assunto cobrado na assertiva.
Minha contribuição.

Proposição simples e composta

Simples: O gato é amarelo. = A

Composta: Se o gato é amarelo, então choveu ontem. = A -> B

Abraço!!!
Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais” é uma proposição lógica SIMPLES.
ERRADO!

Obs: Proposição simples: é toda sentença fechada declarativa que exprime um pensamento que pode ser verdadeiro ou falso.

Proposição composta: é aquela formada por duas ou mais proposições simples
SIMPLES
- não tem conectivo
- um verbo
- uma informação
COMPOSTA
- têm conectivos ( e / ou / ou ou / se então / se somente se)
- mais de um verbo
- mais de uma informação
Pra cimaaaaaa....
a frase disposta pela banca possui apenas uma ideia central, que está ligada a “Os candidatos”; logo, trata-se de uma proposição simples.
Gabarito: Errado
Principais Dicas:
- Proposição: Sentença afirmativa que possui verbo, pode ser Verdadeira ou Falsa e segue dois prinicpios: não contradição e terceiro excluido.
- Pode ser simples ou composta (apresenta conectivo)
- Principais conectivos: E, OU, OU...OU, SE...ENTÃO e SE...E, SOMENTE SE
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!

ID

1108555

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2014

Provas

CESPE - 2014 - Polícia Federal - Agente Administrativo

Disciplina

Raciocínio Lógico

Assuntos

Considerando que P seja a proposição “Não basta à mulher de César ser honesta, ela precisa parecer honesta”, julgue os itens seguintes, acerca da lógica sentencial.

Se a proposição “Basta à mulher de César ser honesta” for falsa e a proposição “A mulher de César precisa parecer honesta” for verdadeira, então a proposição P será verdadeira.

Alternativas

Certo

Errado

Comentários

Considerando que P seja a proposição “Não basta à mulher de César ser honesta, ela precisa parecer honesta”, julgue os itens seguintes, acerca da lógica sentencial.
Se a proposição “Basta à mulher de César ser honesta” for falsa e a proposição “A mulher de César precisa parecer honesta” for verdadeira, então a proposição P será verdadeira.

Certo,
Pois Não basta a mulher de Cezar ser honesta será V,já que como diz a questao: basta a mulher de ser honesta ,é falsa.

E a outra proposição : a mulher de Cesar precisa parecer honesta é V,pois como diz o próprio enunciado que é V

Como elas estão ligadas pelo conectivo “e”

Fica:P^Q ,onde V^V ,vai dar V. Proposições ligadas por “e” será “Verdadeira” quando todas forem “V”
F ---> V = V (certo)
JUSTIFICATIVA do CESPE– A proposição P pode ser expressa por p^q, em que p e q são, respectivamente, as proposições “não basta à mulher de César ser honesta” e “a mulher de César precisa parecer honesta”. De acordo com as hipóteses do item, p e q são verdadeiras, de modo que também o é a proposição P: p^q.
Só reforçando! Não esqueçamos que o que é pedido é proposição na sua forma original, ou seja, do enunciado.
Negou a primeira proposição que seria a negação da original, logo a confirmou, e manteve a segunda. Sendo essa uma proposição composta ligada implicitamente pelo conectivo "e", ambas precisam ser verdadeiras.
Questão correta.
P= ~B^H - (“não basta à mulher de César ser honesta” e “a mulher de César precisa parecer honesta”)
(negar o B): P= V^V=V
B=F
H=V
alguem pode dizer pq se trata de disjunção e não de uma condicional.
“Não basta à mulher de César ser honesta, ela precisa parecer honesta” = ~ MH ^ PH = trata-se uma conjunção ( ^ ) para ser verdadeira todas as premissas precisam ser verdadeiras.

“Basta à mulher de César ser honesta” for falsa = MH

“A mulher de César precisa parecer honesta” for verdadeira = PH

então a proposição P será verdadeira. SIM SERÁ porque ao negar o MH você o torna Verdadeiro:

~ ( ~MH ) ^ PH = V

V ^ V = V
Ela é conjunção devido ao fato de: (mulher ser honesta) E (mulher parecer honesta). P^Q.

Não há condicional
Na pergunta não tem negaçao está escrito da seguinte forma "basta a mulher... e não o não basta que esta escrito no texto e não na pergunta.

Questão passivel de anulação pois P ^ Q para serem verdadeiros necessitam que ambos sejam verdadeiro.
Fiz rápido e nem prestei atenção a questão propõe a frase no sentido "positivo" o enunciado da questão está "negativo"... Portanto troca-se de valor... F para V...

Deus o Abençoe!!

#focoinss2015/2016
O que dá o sentido de "E" é o "NÃO" e o "ELA". Esse não, não está negando nada.

"Não basta à mulher de César ser honesta, ela precisa parecer honesta" significa na verdade:

A mulher de cesar precisa: ser honesta (A) ^ (B) parecer honesta.
P: ~(Ser) ^ Pa

Logo: “Basta à mulher de César ser honesta” (Ser), for F e “A mulher de César precisa parecer honesta” (Pa) for V, então teremos: ~(F) ^ (V) = V^V = V.

Gabarito: C
P:Basta à mulher de César ser honesta”(F)

Q:A mulher de César precisa parecer honesta(V)

P->Q=V

Espero ter ajudado .

TOMA !
INSS 2016

Não ajudou não, está errada sua forma de pensar.

Considerando que P seja a proposição “(1)Não basta à mulher de César ser honesta, (2)ela precisa parecer honesta”, julgue os itens seguintes, acerca da lógica sentencial.

(1)
"Basta à mulher de César ser honesta" = F (Conforme diz a questão), ENTÃO
"Não basta à mulher de César ser honesta" = V

2)
"ela precisa parecer honesta" IGUAL à "mas ela precisa parecer honesta" = V (Conforme diz a questão)

Ora, Se a proposição (1) é VERDADEIRA e a proposição (2) também é VERDADEIRA, como temos o conectivo "mas", dando sentido de "e".
teremos a seguinte representação simbólica V ^ V = V. logo ...

GAB. CORRETO

"TOMA! seu "TOMA!"
V ^ V = V .... pronto!!!
Não encontrei o conectivo nesta questão, usei a lógica da negação para responder.
conectivo é o "se entao"
Conectivo é o: ^ (e), por causa da vírgula, a "vírgula" é substituida por "mas" que é o conjunção.
Primeiro vídeo de RLM que vejo em vídeo...
Certa
“Não basta à mulher de César ser honesta, ela precisa parecer honesta”
P: ~ (Basta à mulher de César ser honesta) = F
Q: A mulher de César precisa parecer honesta = V

Negou P = V
Mantém Q = V

Fui por dedução, porque não consegui identificar o conectivo "mas". É claro que não se trata do conectivo "se e somente se" ou "ou... ou...", as demais tabelas "se...então...", "e" e "ou": verdade com verdade = verdade.
Não precisar fazer tabela verdade:

MULHER DE CÉSAR SER HONESTA ----> A MULHER DE CÉSAR PRECISAR PARECER HONESTA

F V = V

ÚNICO CASO QUE É FALSO:

V---->F= FALSO
Não entendi essa questão o cespe considerou ela errada.

http://www.cespe.unb.br/concursos/dpf_13_administrativo/arquivos/DPF14_009_01.pdf

questão 24.
https://www.youtube.com/watch?v=Fz52Yi4sVSg

A partir de 4min58s
F->V=V
O conectivo oculto pela vírgula é o ^.

“Basta à mulher de César ser honesta” for falsa e a proposição “A mulher de César precisa parecer honesta” for verdadeira

Considerando que P seja a proposição “Não basta à mulher de César ser honesta, ela precisa parecer honesta”

~ F V

Então: ~F ^ V = V ^ V = Verdade

Na dúvida do conectivo, nesse caso, poderíamos lembrar que VV só dará falso se for disjunção exclusiva, nos demais será sempre verdadeiro.
Basta à mulher de César ser honesta = Falsa

Não basta à mulher de César ser honesta = Verdadeira

A mulher de César precisa parecer honesta = Verdadeira

P: "Não basta à mulher de César ser honesta, ela precisa parecer honesta": V ^ V = V
P: Não basta à mulher de César ser honesta, ela precisa parecer honesta

~ (F/\ V)

~(F) é V. Portanto, proposição P é Verdadeira CERTO
Essa questão foi dada como errada pela cespe. Segue a justificativa da banca:

JUSTIFICATIVA – Não é possível expressar a proposição P (que é centrada nos verbos “bastar” e “precisar”) por causa das proposições dadas no item (que são centradas nos verbos ser e parecer). Assim, não é possível valorar a proposição P com base nos valores lógicos das proposições dadas no item.

link: http://www.cespe.unb.br/concursos/dpf_13_administrativo/arquivos/DPF14_009_01.pdf

...

Se ainda não entendeu, acesse o seguinte vídeo, mais precisamente aos 06:24

https://www.youtube.com/watch?v=Fz52Yi4sVSg
IURI ARAÚJO, VOCÊ ESTÁ ENGANADO. Você confundiu a quesão 23 com a 24.

Considerando que P seja a proposição “Não basta à mulher de César ser honesta, ela precisa parecer honesta”, julgue os itens seguintes, acerca da lógica sentencial.

23 Se a proposição “Basta à mulher de César ser honesta” for falsa e a proposição “A mulher de César precisa parecer honesta” for verdadeira, então a proposição P será verdadeira. JUSTIFICATIVA – A proposição P pode ser expressa por p^q, em que p e q são, respectivamente, as proposições “não basta à mulher de César ser honesta” e “a mulher de César precisa parecer honesta”.

De acordo com as hipóteses do item, p e q são verdadeiras, de modo que também o é a proposição P: p^q.
V ^ V = V A proposição dada é uma conjunção aditiva (e)

Puta que pariu, tem uns comentários nada a vê aqui. Tem gente falando que é condicional. Dai-me paciência. Além disso falou que o valor lógico da primeira é Falso. Sem dúvida não entendeu a questão.
Conectivo ocultos quando tem:
virgula + mas = P,masQ = conectivo E

Ou só = P,Q = P e Q
Se a proposição “Basta à mulher de César ser honesta” for falsa e a proposição “A mulher de César precisa parecer honesta” for verdadeira, então a proposição P será verdadeira. CORRETA.

É uma conjunção.

P^Q

“Basta à mulher de César ser honesta” (F)

“A mulher de César precisa parecer honesta” (V)

Agora é só jogar os valores na proposição P:

“Não basta à mulher de César ser honesta (V), ela precisa parecer honesta (V)” = V.
Macete para os conectivos "E" e "OU"= EVVOFF: No "E" só é verdadeira se todas forem verdadeiras: EVV; e no "OU" só é falso quando todas forem falsas: OFF

Sabendo disso já da pra matar muitas quetões, lembrem-se do EVVOFF!
OUUU.....PROFESSORA ENRROLADA DO CACETE??????????????
Considerando que P seja a proposição “Não basta à mulher de César ser honesta, ela precisa parecer honesta”, julgue os itens seguintes, acerca da lógica sentencial.

Se a proposição “Basta à mulher de César ser honesta” for falsa e a proposição “A mulher de César precisa parecer honesta” for verdadeira, então a proposição P será verdadeira.

Se a proposição “Basta à mulher de César ser honesta” for falsa, logo a proposição "Não basta à mulher de César ser honesta" será vedadeira.

A proposição "A mulher de César precisa parecer honesta" é verdadeira.

Logo, a proposição P1 é Verdadeiro e Verdadeiro.
Uma dúvda que pode ter surgido na hora da prova:

A questao seria uma CONJUÇAO (P ^ Q) ou uma CONDICIONAL (P ->Q)?

A questao é uma conjuçao devido a VIRGULA (que significa ^) e pelo fato de nao haver no primeira proposiçao nenhum SE, QUANDO (que sinalizaria para uma condiconal)
~F ^ V =

V ^ V = V
os comentários daqui são melhores q dos professores
Essa professora faz quem ja esta confuso ficar ainda mais. S.O.S
Questão correta!
v^v=v
Não basta à mulher de César ser honesta, ela precisa parecer honesta.
GABARITO CORRETO.
p^q = V^V = VERDADEIRO.
Não sei se é condicional ou conjunção eu sei que se as duas são V independete de ser conjunção, condicional, disjunção, bicondicional. Vai ser v
(~F) ^ V = V
Basta construir a tabela verdade com cada proposição e verificar a linha onde as informações são correspondente:
d = basta a mulher de cezar ser honesta
~d = não basta a mulher de cezar parecer honesta
q = a mulher de cezar precisa parecer honesta
P = ~d ^ q = não basta a mulher de cezar parecer honesta, ela precisa parecer honesta

| d | ~d | q | ~d ^ q = P |
| f | v | v | f |
| f | v | f | f |
| v | f | v | v | <- nesta linha
| v | f | f | f |

Naquela linha, "basta que a mulher de cezar ser honesta" é falso e "A mulher de cezar precisa parecer honesta" é verdade, assim, o resultado daquela linha (~d^q = P) é verdade.
Galera, para ser sucinto: Se isso (“Basta à mulher de César ser honesta” for falsa e a proposição") é falso, logo isso aqui (“Não basta à mulher de César ser honesta") é verdadeiro.
Então “Não basta à mulher de César ser honesta (VERDADEIRO), (vírgula é um conjunção "e") ela precisa parecer honesta (VERDADEIRO). Sendo assim V e V = V.
Bem, não sei se já reparou, note que na questão existe primeiro um " Se" depois o " Então ", dando na mesma resposta de Verdadeiro.
Veja: Se “Basta à mulher de César ser honesta” : falsa, então “A mulher de César precisa parecer honesta”: verdadeira, temos:

F -> V: V, logo, questão certa.

Outro raciocínio seria: “Basta à mulher de César ser honesta” : falsa e “A mulher de César precisa parecer honesta”: verdadeira, temos:

Não basta à mulher de César ser honesta (V), ela precisa parecer honesta (V)
V e V: V, logo, questão certa.
A: nao basts ser honesta
B: precisa ser honesta
A^B
A questão quer saber dados:
Não basta ser honesta sendo falso
Precisa ser honesta sendo verdade
(Não A )= F

(B) = V
Pela questão temos:
A(v) pq o enunciado diz que não A é falso
B(v) pq o enunciado diz que B é verdade
Então V com V só pode dar V
Gabaraito: certo
P: “Não basta à mulher de César ser honesta, ela precisa parecer honesta” (P ^ Q)
1º - Se é mentira que “Basta à mulher de César ser honesta”, então é verdade que "não basta à mulher de César ser honesta", logo, a primeira parte da proposição "P" é verdadeira.
2º - Se é verdade que “A mulher de César precisa parecer honesta”, então a segunda parte da proposição "P" também é verdadeira.
CONCLUSÃO: Sendo verdadeiras ambas as proposições simples de P ^ Q, a proposição, em seu todo, será verdadeira.
otima questao para salvar no caderno !
Para mim, o termo "não basta" não é uma negação, mas sim uma adição, que caracteriza o conector E. Isso pode ser comprovado quando retiramos o termo da frase.

Basta a mulher de Cesar ser honesta, ela precisa parecer honesta.

A própria justificativa do cespe invalida a questão, ao não interpretar a proposição como ~P e Q, mas sim como P e Q.

JUSTIFICATIVA do CESPE– A proposição P pode ser expressa por p^q, em que p e q são, respectivamente, as proposições “não basta à mulher de César ser honesta” e “a mulher de César precisa parecer honesta”. De acordo com as hipóteses do item, p e q são verdadeiras, de modo que também o é a proposição P: p^q.
NÃO basta ser honesta..(V) Precisa parecer honesta(V) V>>V=V
Basta ser honesta?Não (F) Precisa parecer honesta(V) F>>V=V
Apenas V >>F é falsa
Questão Certa
esse conectivo oculto deixa a questão difícil.
Proposição P: Não basta à mulher de César ser honesta, ela precisa parecer honesta.

A: Não basta à mulher de César ser honesta
B: ela precisa parecer honesta

A ^ B => V
V ^ V => V

~A: Basta à mulher de César ser honesta
B: A mulher de César (ela) precisa parecer honesta

~A ^ B => F
F ^ V => F

A negação de "Ñ Basta..." é "Basta...", isto é, negação de A é ~A, se ~A é falso A é verdadeiro, conforme o esquema acima a proposição P é verdadeira.

Achei mais claro assim.
Minha contribuição.

Tabela verdade da conjunção:

V ^ V = V
V ^ F = F
F ^ V = F
F ^ F = F

Abraço!!!
Como vcs acharam o conectivo?
Quem estuda conjunções em português, sabe o valor desse conectivo.
Não só... mas também.

Não basta ser,apenas, concurseiro; tem que estudar.
Cuidado amigos, muitos comentários equivocados, trata-se do conectivo "E", aplicado de forma oculta, sendo assim, não basta ela ser honesta, ela teria que ser honesta "E" parecer honesta, desta forma, no enunciado diz que a primeira parte da preposição sendo dita desta forma, " basta a mulher ser honesta é falsa ", sendo assim, a primeira parte da preposição é verdadeira, já que é o oposto dessa, a segunda parte é dita como verdadeira, então vamos usar a tabela do 'E" para certificar-se. Dividiremos a primeira parte da sentença denominada por A e a segunda por B.
A: V e B:V

Encontrada na tabuada.
E
A ^ B
V V = V <----
V F = V
F V = V
F F = V
Certo
Muitas vezes, onde tem vírgula é omitida uma conjunção. Portanto, reescrevendo a frase: Não basta à mulher de César ser honesta, _mas_ ela precisa parecer honesta. Houve uma vírgula para omitir “mas”, e “mas’" na lógica é substituído por “e”.
Para uma conjunção ser verdadeira, uma das suas proposições necessitam ter valor lógico verdadeiro.
No caso em tela, uma proposição é verdadeira, pois ambos de seus valores lógicos são verdadeiros ao final.
Não basta à mulher de César ser honesta (V), ela precisa parecer honesta (V).
f -> v = v
FORÇOU MUITO ESSE "E" ENTENDI COM SE... ENTAO...
Questões que o CESPE elabora só para eles mesmos interpretarem entre si ou para distribuir entre videntes. Interessante notar em alguns comentários a declaração de que P (F) ^ Q (V) = V, quando na conjunção o valor só será verdadeiro se todas as proposições forem verdadeiras. Charlles, o mundo não é mais o mesmo.
Primeira preposição:

P ^ Q

~P = Falsa
Q= Verdadeira

Logo: P (Verdadeira) ^ Q (Verdadeira)
Complementando os comentários dos colegas

A banca Cespe sempre brinca com as conjunções e conectivos, por isso temos que ficar atentos ao contexto!!

Nesta questão o "BASTA" não foi usado com sentido de "se .. então" como costuma ser usado pela banca, mas sim como "e" conjunção => Leia assim: “Não basta à mulher de César ser honesta,(mas também) ela precisa parecer honesta”,

Segue um exemplo (Q853839 TRT2017) em que o Basta foi usado com sentido de "Se.. então"
“Basta um de nós mudar de ideia e a decisão será totalmente modificada.”

Bons estudos!!
Eu fui no gosto e errei. Não tinha entendido que tinha que transformar a falsa em verdadeira.
A proposição P diz exatamente que é falso que "Basta a Mulher de César ser honesta" e verdadeiro que "Ela precisa parecer honesta".
P: “Não basta à mulher de César ser honesta (V), ela precisa parecer honesta” (V).

Q: “Basta à mulher de César ser honesta” . FALSA
R: “A mulher de César precisa parecer honesta” . VERDADEIRA

Então P: Verdadeira ^ Verdadeira.
Logo, é verdadeira, visto que temos uma conjunção.

ID

1132756

Banca

Prefeitura do Rio de Janeiro - RJ

Órgão

Prefeitura de Rio de Janeiro - RJ

Ano

2013

Provas

Prefeitura do Rio de Janeiro - RJ - 2013 - Prefeitura de Rio de Janeiro - RJ - Guarda Municipal

Disciplina

Raciocínio Lógico

Assuntos

Considere as seguintes proposições:

p : O Rio de Janeiro é uma cidade maravilhosa.
q : Os turistas amam o Rio de Janeiro.

A sentença que representa a proposição ~ p ^ q está indicada na seguinte alternativa:

Alternativas

O Rio de Janeiro é uma cidade maravilhosa e os turistas não amam o Rio de Janeiro.

O Rio de Janeiro não é uma cidade maravilhosa e os turistas amam o Rio de Janeiro.

O Rio de Janeiro não é uma cidade maravilhosa ou os turistas amam o Rio de Janeiro.

O Rio de Janeiro é uma cidade maravilhosa ou os turistas não amam o Rio de Janeiro.

Comentários

Temos que :
p: O Rio de Janeiro é uma cidade maravilhosa.
~p: O Rio de Janeiro não é uma cidade maravilhosa.
O conectivo ^ representa uma conjunção, assim ~ p ^ q será:
O Rio de Janeiro não é uma cidade maravilhosa e os turistas amam o Rio de Janeiro.
Letra B.
Gabarito B
(~ p) O Rio de Janeiro não é uma cidade maravilhosa(^ q) e os turistas amam o Rio de Janeiro.
p : O Rio de Janeiro é uma cidade maravilhosa.
q : Os turistas amam o Rio de Janeiro.
O símbolo ~ significa NEGAÇÃO e ^ quer dizer ''E'' (Conjunção).
Dada a sentença: ~ p ^ q, é o mesmo que:
O Rio de Janeiro NÃO é uma cidade maravilhosa E os turistas amam o Rio de Janeiro.
Que venham 1000 questões assim no INSS :)
Olá pessoal,

Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/MQmlVNkDqYs

Professor Ivan Chagas
www.gurudamatematica.com.br

ID

1138750

Banca

PONTUA

Órgão

Prefeitura de Jaguarão - RS

Ano

2013

Provas

PONTUA - 2013 - Prefeitura de Jaguarão - RS - Advogado

Disciplina

Raciocínio Lógico

Assuntos

Assinale a alternativa que traduz CORRETAMENTE para o Cálculo Quantificacional Clássico a sentença abaixo, sendo que A: “x é um animal” e M: “x é um mamífero”:

“Nem todos os animais são mamíferos”

Alternativas

x ( Ax

Mx )

x ( Ax

Mx)

x ( Ax

Mx )

As alternativas “b” e “c” estão corretas.

As alternativas “a” e “b” estão corretas.

Comentários

a) Nem todo animal é mamifero.
b) Existe animal que não é mamífero.
A e B estão certas, logo a alternativa E é a mais correta. É assim que as bancas consideram, a mais correta é aquela que diz quais estão certas, ou quais estão erradas, etc. Considerem sempre essa como gabarito oficial ao se depararem com esse tipo de questão.

Alternativa A diz: Não é verdade que, todos os animais estão contidos no conjunto dos mamíferos (CERTO)
Alternativa B diz: Existe um ser que pertençe ao o conjuntos dos animais e ao conjunto dos não-mamíferos (CERTO)
Alternativa C diz: Todos os animais estão contidos no conjunto dos mamíferos (ERRADO)
Alternativa D diz: B e C estão corretas (ERRADO)
Alternativa E diz: A e B estão corretas (como já explicado, as bancas sempre consideram essa a resposta mais certa)
Interpretando cada alternativa:

Alternativa A: Não é verdade que, todos os animais estão contidos no conjunto dos mamíferos

Alternativa B: Existe um ser que pertence ao o conjuntos dos animais E ao conjunto dos não-mamíferos.

Alternativa C: Todos os animais estão contidos no conjunto dos mamíferos.

Logo, avaliando cada alternativa, concluímos que A e B estão corretas e a C errada.

Resposta: Alternativa E.
Alguém poderia explicar melhor essa questão?
Nem todos os animais são mamíferos

SE É A, ENTÃO É M

A - CORRETO: A --> M
B - CORRETO: ~(A ^ ~M) (negação da negação é igual verdadeiro)

GABARITO ''E''
“Nem todos os animais são mamíferos” , significa que conjunto A interseção com o conjunto B não é um conjunto vazio e A não está contido em B.
Alternativa A: Nem todos os elementos do conjunto animais estão contidos no conjunto mamíferos. (C)
Alternativa B: Existe elementos do conjunto animais que são interseção com o conjunto não-mamíferos. (C)
Alternativa C: Todos os elementos do conjunto animais estão contidos no conjunto dos não-mamíferos. (E)
v - união; ^ - interseção; -> - está contido; - igualdade

ID

1145761

Banca

PC-SP

Órgão

PC-SP

Ano

2010

Provas

PC-SP - 2010 - PC-SP - Escrivão de Polícia Civil

Disciplina

Raciocínio Lógico

Assuntos

Qual das alternativas abaixo não pode ser considerada uma proposição?

Alternativas

7 < 9

Pelé é o nome de um planeta.

A lua é um satélite da terra.

X > 2

A capital de Sergipe é Teresina.

Comentários

Alternativa D: Trata-se de uma sentença aberta pois não pode ser valorada e por isso nuncapoderá ser considerada uma proposição.

BONS ESTUDOS!!!
Deve-se analisar as alternativas na ordem das exceções:

-> Quando NÃO será proposição:

- Quando for uma pergunta

- Quando for uma exclamativa

- Quando for pedido

- Quando for promessa

- Quando for sentença aberta.

OBS: Sentença aberta é quando o sujeito não está definido.

Gabarito: D
X > 2 ( NÃO POSSO ATRIBUIR O VALOR DE X, MUITO MENOS DIZER SE É FALSO OU VERDADEIRO ESTÁ PROPOSIÇÃO )
Incógnitas não pode ser considerado proposição.

ID

1149811

Banca

UERR

Órgão

PM-RR

Ano

2013

Provas

UERR - 2013 - PM-RR - Soldado da Polícia Militar

Disciplina

Raciocínio Lógico

Assuntos

Qual das sentenças declarativas abaixo NAO é uma proposição?

Alternativas

O Brasil é o maior país da América do Sul.

Todos os paulistas são brasileiros.

Um ano tem 365 dias.

A baleia é um peixe.

-5 > 2.

Comentários

Existe ano com 365 dias (normal) e ano com 366 dias (bissexto). Dentre as questões, a única que apresenta uma incógnita (neste caso, saber de qual ano ele está se referindo..."um ano" não define se a declaração fala do ano normal ou do ano bissexto) é a alternativa "c".
Achei a questão meio errada... Acertei porque todas tem o verbo "é" menos a que usa o verbo "tem".
Acertei porque chutei (chute consciente - parecia a menos certa).

Aceito a explicação do colega e exatamente por ela considero que seria muito difícil eu acertar de novo a não ser pelo chute novamente.
Aí consistiu a minha dúvida. A definição de proposição é justamente o fato de ser possível julgar entre verdadeiro ou falso. Um ano pode ter 365 dias ou não.
O gabarito está errado. R: E
Pra mim o gabarito está errado.
A resposta é letra C, pois existem anos bissextos
item E , é uma proposição. sentenças matemáticas são proposições, com excessão das sentenças abertas que aparentemente não não sabemos o valor se cara. ex; x+2 =10. (sentença aberta, não é proposição.) ex. -5>2 é proposição.
uma questão dessa é C de cristo
PROCURA O VERBO DA PROPOSIÇAO, E SE PODE VALIDAR (F) OU (V). PARA AS QUESTOES COM NUMEROS OBVIO Q NAO PRECISA DE VERBO.
a) O Brasil é o maior país da América do Sul. é uma proposição pois pode ser valorada em verdadeiro e falso e possui verbo e sujeito.

b) Todos os paulistas são brasileiros. é uma proposição pois possui verbo e sujeito e pode ser valorada como verdadeiro ou falso.

c) Um ano tem 365 dias. NAO É PROPOSIÇÃO, não tem como identificar o sujeito, QUAL ANO em específico tem 365 dias? pois existe ano bissexto e por esse motivo não é proposição, pela ausência de sujeito específico.

d) A baleia é um peixe. é proposição pois existe verbo, sujeito e valor lógico.

e) -5 > 2. é proposição por possui elementos claros, e poder ser valorada em verdadeiro ou falso

ID

1149814

Banca

UERR

Órgão

PM-RR

Ano

2013

Provas

UERR - 2013 - PM-RR - Soldado da Polícia Militar

Disciplina

Raciocínio Lógico

Assuntos

Considerando o valor lógico das proposições p, q e r , assinale a única proposição que tem valor lógico verdadeiro.

p: A capital do Estado da Bahia é Vitória.
q: A Terra gira em torno do Sol.
r: A 1º Guerra Mundial terminou em 1945.

Alternativas

p ^ q

q ^ ~r

Comentários

p - F
q - V
r - F
a) F
b) F ^ V = F
c) F v F = F
d) V ^ V = V
e) F v F = F

Assim, a única que tem valor lógico V é a d.
O chato foi uma questão de história junto da de raciocínio. Mas mesmo assim dá pra resolver com lógica.
Gente, ainda não aprendi lógica, mas cuidado!
Não são premissas!
Cada frase corresponde a um enunciado que deve ser interpretado para que as respectivas letras p, q e r possuam um valor verdadeiro ou falso. Depois dessa interpretação a questão se torna fácil.
Vejamos: A capital da Bahia - Salvador, logo: p= F ; A terra gira em torno do sol correto, logo: q= V ; A segunda guerra terminou em 1945, logo: r= F.... agora basta que façamos a tabelinha...
ficará assim
letra a nem precisa fazer
letra b) p ^ q = F
letra c) p v r = f
letra d) q ^ ~r = v
letra e ) p v ~q = f
letra d resultado v
A segunda guerra terminou em 1945, e não a peimeira como diz a questão.

Por esse motivo errei, não prestei atenção na informação.
Tambem errei a questão devido nao prestar atenção que foi a segunda guerra mundial que terminou em 1945
ATENÇÃO!
Na atualidade, perguntar/afirmar "verdades universais" pode gerar transtorno...

Se fosse perguntado/afirmado A TERRA É REDONDA, haveria alguns candidatos tentando recurso ou anulação...
kkkkkkkkkkkkk
p - F
q - V
r - F

Só fazer a tabela !!!

ID

1149817

Banca

UERR

Órgão

PM-RR

Ano

2013

Provas

UERR - 2013 - PM-RR - Soldado da Polícia Militar

Disciplina

Raciocínio Lógico

Assuntos

Considerando o valor lógico das proposições p, q e r , assinale a única proposição que tem valor lógico falso.

p: Onze é um número primo.
q: Evaporação é a passagem do estado sólido para o gasoso.
r: O cloreto de sódio é utilizado para cozinhar.

Alternativas

Comentários

Alternativa "A".
P: Onze é um número primo.
Valor lógico de P = F
Q: Evaporação é a passagem do estado sólido para o gasoso
Valor lógico de Q = F, essa F adotado pela questão parti do senso comum de que a evaporação é a passagem do do estado líquido para o gasoso, precisamente a evaporação refere-se muito mais ao agitação molecular do ao estado físico em si, falo isso mesmo ciente que os estados físicos dependem dependem da agitação molecular para serem denominados de tal e tal forma, o que quero dizer com isso é que a questão deveria ser objetivo e não ambígua em suas afirmações.
Dizer: "evaporou do sólido para o gasoso" parece estranho para quem não é da área da química, mas é perfeitamente possível, assim ocorre com a naftalina (aquelas bolinhas brancas que se coloca em roupa para não dar morfo), elas evaporam do sólido para o líquido.
R: O cloreto de sódio é utilizado para cozinhar
Valor lógico de R= V
Em grossas palavras, usamos sal de cozinha na comida.
Pessoal, perdão se estou falando besteira, apenas estou expressando minha opinião, sintam-se à vontade para contestar.
Abraço.
A LUTA CONTINUA!

Curiosidade!
O que é um número primo?
Número primo é um número inteiro que admite exatamente 4 divisores.

O conceito sobre números primos para inteiros engloba tanto números positivos como negativos.

Os únicos divisores de 3 são {-3, -1, 1, 3}. O número 3 é primo.

Os únicos divisores de -17 são {-17, -1, 1, 17}. O número -17 é primo.

Os únicos divisores de 2 são {-2, -1, 1, 2}. O número 2 é primo.

Os únicos divisores de 1 são {-1, 1}. O número 1 não é primo.

Os únicos divisores de 6 são {-6, -3,-2, -1, 1, 2, 3, 6}. O número 6 não é primo.

Muita gente descuidada acha estranho esta forma de apresentar o conceito de números primos porque acreditam que a definição somente se aplica e somente se restringe aos números NATURAIS, quando a definição é, na verdade, extensível a todos os INTEIROS.

A frase "um número é primo se for divisível por 1 e por ele mesmo" é imprecisa quanto à restrição de qual conjunto numérico deveremos tomar o candidato a primo (pode ser natural ou inteiro) e permite que 1 seja primo porque (sim) é divisível por 1 e (sim) é divisível por ele mesmo.

Enfim, usar a frase "um número é primo se for divisível por 1 e por ele mesmo" traz alguns problemas, contornáveis, mas precisa ser evitada. Um inteiro é primo se tiver exatamente 4 divisores e PONTO. Fonte: http://www.profcardy.com/cardicas/tirateima.php?id=2
Alternativa "A".
P: Onze é um número primo.
Valor lógico de P = F
Q: Evaporação é a passagem do estado sólido para o gasoso
Valor lógico de Q = F, essa F adotado pela questão parti do senso comum de que a evaporação é a passagem do do estado líquido para o gasoso, precisamente a evaporação refere-se muito mais ao agitação molecular do ao estado físico em si, falo isso mesmo ciente que os estados físicos dependem dependem da agitação molecular para serem denominados de tal e tal forma, o que quero dizer com isso é que a questão deveria ser objetivo e não ambígua em suas afirmações.
Dizer: "evaporou do sólido para o gasoso" parece estranho para quem não é da área da química, mas é perfeitamente possível, assim ocorre com a naftalina (aquelas bolinhas brancas que se coloca em roupa para não dar morfo), elas evaporam do sólido para o líquido.
R: O cloreto de sódio é utilizado para cozinhar
Valor lógico de R= V
Em grossas palavras, usamos sal de cozinha na comida.
Pessoal, perdão se estou falando besteira, apenas estou expressando minha opinião, sintam-se à vontade para contestar.
Abraço.
A LUTA CONTINUA!

Curiosidade!
O que é um número primo?
Número primo é um número inteiro que admite exatamente 4 divisores.

O conceito sobre números primos para inteiros engloba tanto números positivos como negativos.

Os únicos divisores de 3 são {-3, -1, 1, 3}. O número 3 é primo.

Os únicos divisores de -17 são {-17, -1, 1, 17}. O número -17 é primo.

Os únicos divisores de 2 são {-2, -1, 1, 2}. O número 2 é primo.

Os únicos divisores de 1 são {-1, 1}. O número 1 não é primo.

Os únicos divisores de 6 são {-6, -3,-2, -1, 1, 2, 3, 6}. O número 6 não é primo.

Muita gente descuidada acha estranho esta forma de apresentar o conceito de números primos porque acreditam que a definição somente se aplica e somente se restringe aos números NATURAIS, quando a definição é, na verdade, extensível a todos os INTEIROS.

A frase "um número é primo se for divisível por 1 e por ele mesmo" é imprecisa quanto à restrição de qual conjunto numérico deveremos tomar o candidato a primo (pode ser natural ou inteiro) e permite que 1 seja primo porque (sim) é divisível por 1 e (sim) é divisível por ele mesmo.

Enfim, usar a frase "um número é primo se for divisível por 1 e por ele mesmo" traz alguns problemas, contornáveis, mas precisa ser evitada. Um inteiro é primo se tiver exatamente 4 divisores e PONTO. Fonte: http://www.profcardy.com/cardicas/tirateima.php?id=2
Onze é um número primo - Valor lógico Falso? Não entendi, onze é sim um número primo, logo P = V. Aliás, caso P tenha valor lógico F, logo o item D estaria, também, correto, pois seu resultado seria Falso, como pede a questão!
Gutemberg, vc está certo. 11 é sim um número primo.
P = V
Q = F
R = V
P = V
q= F
r = v
logo a questão falsa seria a (b)
pois na condicional v e F = F
Gostaria de saber o que significa as setas?
Amigo rodrigo, Aconselho você a assistir umas aulas de Conectivos Lógicos no youtube possuem varias aulas grátis. Será mais facil de sua pergunta ser respondida ... Abraços e boa sorte.
Julgando as proposições:
p: Onze é um número primo - V
q: Evaporação é a passagem do estado sólido para o gasoso- F ( o correto seria do líquido para o gasoso)
r: O cloreto de sódio é utilizado para cozinhar - V ( o famoso sal de cozinha)
Julgando as alternativas:
a) q <-> r
F<->V - F
b) q->~r
F-> ~V
F->F - V
c) ~r->~p
~V-> ~V
F-> F - V
d) p<->~q
V<-> ~F
V<-> V - V
e) p-> r
V -> V - V
Logo, a única que tem valor lógico falso é a letra A.
Meu Deus, estou perdida!!! Já estudei conectivos lógicos, estou por dentro do assunto. Mas não consigo fazer a questão. Alguém me ajuda com o passo a passo pra resolver.
p: Onze é um número primo. (Primos têm apenas dois divisores diferentes) VERDADE
q: Evaporação é a passagem do estado sólido (LÍQUIDO) para o gasoso. FALSO
r: O cloreto de sódio é utilizado para cozinhar. VERDADE
A) q <--> r
F <--> V = FALSO (GABARITO)
OBS: Na Bicondicional só é verdade quando as duas são iguais,
V <--> V = V
F <--> F = V
Evaporação é a passagem do estado sólido para o gasoso. PODE CONFUNDIR OS DESAVISADOS.
R/ A

ID

1168165

Banca

VUNESP

Órgão

PC-SP

Ano

2014

Provas

VUNESP - 2014 - PC-SP - Delegado de Polícia

Disciplina

Raciocínio Lógico

Assuntos

Os conectivos ou operadores lógicos são palavras (da linguagem comum) ou símbolos (da linguagem formal) utilizados para conectar proposições de acordo com regras formais preestabelecidas. Assinale a alternativa que apresenta exemplos de conjunção, negação e implicação, respectivamente.

Alternativas

¬ p, p v q, p ∧ q

p ∧ q, ¬ p, p -> q

p -> q, p v q, ¬ p

p v p, p -> q, ¬ q

p v q, ¬ q, p v q

Comentários

Gabarito. B.
^ = conjunção
~ ou ¬ = negação
-> = implicação que é a condicional
Além disso:
^ disjunção (inclusiva)

^/ disjunção exclusiva

<->bicondicional
Letra B

Conjunção E (^)

Disjunção OU (V)

Disjunção Exclusiva (v) ou...ou

Condicional se então (→ )

Bicondicional se somente se (↔)
~ ou ¬ = negação
lembrando que o termo implicação lógica só é utilizado quando for uma tautologia

Implicação lógica
Definição

A proposição P implica a proposição Q, quando a condicional P → Q for uma tautologia.

O símbolo P ⇒ Q (P implica Q) representa a implicação lógica.
http://www.colegioweb.com.br/trabalhos-escolares/matematica/nocoes-de-logica/implicacao-logica.html
conjunção : ^
negação: ~ / ¬
condicional / implicação: →
Questão fácil. Quando se confere a primeira conjunção já é possível descobrir a resposta certa.
Na álgebra das proposições temos os seguintes conectivos lógicos:
Negação: ¬ , ~
Conjunção: ^
Disjunção inclusiva: v
Disjunção Exclusiva: _v
Implicação ou condicional: →
Dupla Implicação ou bicondicional: ↔
Negação: ¬ , ~
Conjunção: ^
Disjunção inclusiva: v
Disjunção Exclusiva: _v
Implicação ou condicional: →
Dupla Implicação ou bicondicional: ↔

Usar a sequencia para resolver essa questão.
Letra b.
Símbolo da conjunção: ^
Símbolos da negação: ¬, ~
Símbolo da implicação ou condicional: →
NEGAÇÃO DE CONJUNÇÃO É A DISJUNÇÃO INCLUSIVA: ¬ (P ^ Q) = ¬P V ¬Q

NEGAÇÃO DA DISJUNÇÃO INCLUSIVA É A CONJUNÇÃO: ¬ (P V Q) = ¬P ^ ¬Q

NEGAÇÃO DA DISJUNÇÃO EXCLUSIVA É A BICONDICIONAL: ¬ (P _v Q) = P <->Q

NEGAÇÃO DA BICONDICIONAL É A DISJUNÇÃO EXCLUSIVA: ¬ (P <->Q) = P _V Q

NEGAÇÃO DA CONDICIONAL (ou IMPLICAÇÃO): repete-se a primeira parte, troca-se o conectivo lógico por "e" (^) e nega-se a segunda parte: ¬ (P -> Q) = P ^ ¬Q
Essa questão foi pra não zerar kkkkk
Analisando a questão,

De acordo com os operadores lógicos: conjunção (^), negação (¬) e implicação (→).

RESPOSTA: (B)
Só queria entender por que não caem questões assim na minha prova? :-(
p ∧ q, ¬ p, p -> q
Alternativa: B
Muita Atenção!!
Implicação é o mesmo que condicional
O sinal de negação pode aparecer como ~ ou ¬
Veja o vídeo que gravei com a resolução dessa questão:
https://youtu.be/WX_bsV8XlFA
Professor Ivan Chagas
Não quero questões assim na minha prova, todo mundo acerta! Quero aquela que só eu sei :)
conjunção A /\ B

negação ¬A

implicação A --> B
Sabendo que a conjunção é representada por ^ vc acertaria a questão
De acordo com os operadores lógicos: conjunção (^), negação (¬) e implicação (→).

res. do prof
CONJUNÇÃO (&) p ∧ q

NEGAÇÃO (~) ¬ p

IMPLICAÇÃO (condicional) p -> q
Prova para Delegado?

Nem para tjsp cai fácil assim
Caramba, vou estudar direito para virar delegado. Questão fácil. A gente fala assim mas é com base apenas em uma matéria, o cara tem que saber muito de ouras matérias para tornar-se delegado, fora a prova oral que é animal, já vi um vídeo no youtube uma vez.
Olá pessoal,

Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/_EaL3st8ADo

Professor Ivan Chagas
www.gurudamatematica.com.br
Essa Vunesp é uma mãe, hein!
^ Conjunção
v Disjunção inclusiva
¬ Negação
-> condicional

GABARITO -> [B]
foi-se o tempo
podia ter começado a fazer concurso quando caia questões assim kkkk
Conjunção pode ser representado por ( ^ ) ou ( e )
.
Negação pode ser representado por ( ~ ) ou ( ¬ )
.
Implicação pode ser representado por ( -> ) ou ( se,..., então ) ou ( pelo nome de CONDICIONAL )
Gabarito letra B
Implicação é Condicional, conjunção é o E ( ^ ) e negação é cantoneira( ¬ ) ou ~.
* P Ʌ Q, ¬ P, P → Q - Temos conjunção, negação e implicação, respectivamente.
Os símbolos que representam a conjunção, a negação e a condicional (implicação), são, respectivamente, o ‘Ʌ’, o ‘¬’ e o ‘→’.
Conjunção (E): ^ ou &
Disjunção Inclusiva/Simples (OU): v
Disjunção Exclusiva (Ou... ou...): v
Condicional/Implicação (Se...então...): ->
Bi condicional/ Bi implicação (Se e somente se): <->
Negação: ~ ou ¬

ID

1169614

Banca

VUNESP

Órgão

PC-SP

Ano

2014

Provas

VUNESP - 2014 - PC-SP - Investigador de Polícia

Disciplina

Raciocínio Lógico

Assuntos

Para a resolução das questões de números 84 e 85, considere a seguinte notação dos conectivos lógicos:

∧ para conjunção, ∨ para disjunção e ¬ para negação.

Uma proposição composta é tautológica quando ela é verdadeira em todas as suas possíveis interpretações.

Considerando essa definição, assinale a alternativa que apresenta uma tautologia.

Alternativas

p ∨ ¬ q

p ∧ ¬ p

¬ p ∧ q

p ∨ ¬ p

p ∧ ¬ q

Comentários

Questão de fácil resolução, basta fazer a construção da tabela verdade:

P	Q	~P	~Q	P V ~Q	P ^ ~P	~P ^ Q	P V ~P	P ^ ~Q
V	V	F	F	V	F	F	V	F
V	F	F	V	V	F	F	V	V
F	V	V	F	F	F	V	V	F
F	F	V	V	V	F	F	V	F

RESPOSTA: ALTERNATIVA "D"

Gabarito. D.
o ou(v) só é falso se o antecedente e o consequente for falso.
P V ~P
V
V
V
V
Letra D. De acordo com as regras da disjunção, a proposição será falsa se todas as sentenças forem falsas, o que não ocorreu. Logo todas as proposições são verdadeiras, formando uma tautologia.
Conjunção ^ = Só é verdadeiro se todos forem verdadeiros

Disjunção v = Só é falso se todos forem falsos
Condicional - --> =Só é falso se o antecendente for V e o consequente for F
....
P u ~P =
V F = V
F V = V
V F = V
F V = V
( nessa questão eu atribui um valor a proposição P e depois inverti seu resultado ou seja ~P)
Para resolver essa questão, deve-se testar cada possibilidade lógica em cada alternativa:

Logo a resposta é letra D.
a) CONTINGÊNCIA

p q ¬ p ¬ q p ∨ ¬ q

V V F F V

V F F V V

F V V F F

F F V V V
b) CONTRADIÇÃO

p q ¬ p ¬ q p ∧ ¬ p

V V F F F

V F F V F

F V V F F

F F V V F
c) CONTINGÊNCIA

p q ¬ p ¬ q ¬ p ∧ q

V V F F F

V F F V F

F V V F V

F F V V F
d) TAUTOLOGIA

p q ¬ p ¬ q p ∨ ¬ p

V V F F V

V F F V V

F V V F V

F F V V V
d) CONTINGÊNCIA

p q ¬ p ¬ q p ∧ ¬ q

V V F F F

V F F V V

F V V F F

F F V V F
A questão apresenta uma tautologia clássica...(ser ou não ser). resolver cada alternativa consumirá muito tempo de prova.
Tautologia --> É uma proposição composta em que todos seus valores são "V"erdadeiros.
Contradição --> É uma proposição composta em que todos seus valores são "F"alsos.
Contingência --> É uma proposição residual, ou seja, não é tautologia nem contradição; apresenta V e F em sua tabela verdade.
Bom, para aquelas pessoas que não "decoraram" nenhuma relação tautológica, só restaria em qualquer hipótese a construção da tabela verdade para cada assertiva.

a) P ∨ ¬ Q

P   Q ¬Q        P V ¬Q    ( Como se nota a valoração "F" mesclada com "V" torna a assertiva uma contingência)
V   V     F      V
V F    V            V
F    V    F       F
F     F   V          V

b) P ^ ¬Q

P       Q    ¬Q          P^ ¬Q    Como se nota a valoração "F" mesclada com "V" torna a assertiva uma contingência)
V       V       F          F
V       F        V       V
F       V        F         F
F       F        V         F

c) ~P ^ Q

P   Q      ¬P       ~P^ Q Como se nota a valoração "F" mesclada com "V" torna a assertiva uma contingência)
V   V F          F
V    F          F    F
F       V         V      V
F        F         V         F

d) P v ¬P

P            Q     ¬P             P v ¬P
V            V             F            V
V            F                F    V
F    V    V           V
F             F               V        V

Tendo em vista, a valoração V em toda resultante da proposição composta estamos diante de uma tautologia.
Macete: proposição V (ou) negação da proposição = sempre será tautologia.
Alternativa D.
Nao entendo oq se pede pra fazer exatamente na questao :/
É a letra D.
VVFF, FFVV= VVVV
p ou não p ; p v ~ p

Chove ou não chove
A porta esta aberta ou fechada; Maria esta viva ou Maria esta morta; O copo quebrou ou não quebrou.
O VALOR LÓGICO vai ser sempre verdadeiro, ou seja, tautologia.
A) VVFV
B) FFFF
C) FFVF
D) VVVV
E) FVFF
iuuuupeee,esta de brincadeira...kkkk
p q ¬p p v ¬p
v v f v
v f f v
f v v v
ff v v
ser OU não ser...grande joselias
LETRA D
Para resolver questão de tautologia mais rápido , lembre da famosa frase de William Shakespeare " Ser (p) ou (v) não ser( ~p) , eis a questão"

CONTINUE ESTUDANDO , VAI CHEGAR A SUA VEZ!
Que questão difícil. Ufa!!
ser ou nao ser
Gabarito: d

P     ~P      P v ~P
V      F           V
F      V           V
P ou não P, eis a questão!
pra quem estuda esta muito bom mais quem não estuda kkkkkk não chegar nem perto gab D
Quebrei a cuca.
Temos que lembrar "A negação de uma negação é uma afirmação"

O gabarito é D porque para o "ou" só da F se todos forem F.

o que nunca vai acontecer porque (p v ~p) é a mesma proposição, e uma é a afirmação e a outra a sua negação.

Com isso, quando uma for V a outra será obrigatoriamente F assim as duas nunca daram F F e o "ou" nunca será falso.

Boa questão.
vamos comigo, na letra D que temos o gabarito, NÃO estamos tratando com proposições diferentes, sim proposições iguais. Logo temos apenas dois valores para a proposição P -> V F / F V

vamos la: P v ¬P , sabebos que com o conectivo V para ser verdade basta apenas uma proposição ser verdade..

aqui temos a proposição P sendo verdade , logo depois do conectivo a negação da verdade no caso (falsidade) P(v) V ¬P(f) = V

a outra possibilidade seria a proposição P sendo falsidade, e logo depois do conectivo a negação (¬) dessa falsidade, tornando verdade P(f) V ¬P(v) = V
Decore as principais tautologias, isso consumirá menos tempo no dia da sua prova.

Tautologias:

pv~p (ser ou não ser, passo ou não passo, chove ou não chove...)

p--->p

~(~p)<--->p

~(p^q)~pv~q

~(pvq)~p^~q

~(p--->q)p^~q

(p--->q)~pvq

(p--->q)~q--->~p

Bons estudos.

Shalom!
Comece pelo OU (v)

se uma for Verdadeira nao precisa olhar a segundA, POIS BASTA QUE UMA SEJA VERDADEIRA PARA TODA SER v
P V ~P

V F= V

V F= V

F V= V

F V= V

É UMA TAUTOLOGIA. PORTANTO, GABARITO D.
alguém pode me explicar por favor,cade o resto da tabela verdade da alternativa D.

na minha deu V V F V
UMA LETRA DUAS LINHAS, 2 LETRAS 4 LINHAS...

P | ~P | P v ~P |

V | F | V

F | V | V

NÃO TEM RESTO!
Explicação do Thiago Trigo está muito melhor que a do professor!
Tautologia sempre lembra ''ser ou não ser''

logo ''per'' ou nao per''

Contradição

Ser e Não ser

logo ''per e nao per''
p ∨ ¬ p

Uma proposição composta é tautológica quando ela é verdadeira em todas as suas possíveis interpretações

Ex:

V v F = V

F v V = V
p p p v p p ~p p v ~p

v v v v f v

v v v v f v

f f f f v v

f f f f v v
Na tautologia, todas as combinações possíveis serão verdadeiras.

Na contradição, todas as combinações possíveis serão falsas.

Na disjunção, haverá uma alternância.
Sabemos que para ser uma tautologia, independentemente das combinações, o valor sempre será verdadeiro.

Então basta apenas tentar negar a proposição, e caso não consiga, será uma tautologia.

Simples, prático e rápido.
p v ~p = SEMPRE SERÁ TAUTOLOGIA
Essa foi fácil porque já sabemos que uma proposição OU sua negação será sempre uma tautologia.

Para os outros casos, a resolução mais simples é forçar um resultado falso em cada alternativa até encontrar a tautologia :D

PAZ
P v ~P

V F V ( No v (ou) só em falso quando tudo é falso ,, não tem nenhum que os dois é F ,, TUDO V = TAUTOLOGIA)
V F V
F V V
F V V
SER OU NÃO SER.

EIS A QUESTÃO

Pv---P
Copiada do Thiago Trigo.
Até eu entendi.

Tautologia --> É uma proposição composta em que todos seus valores são "V"erdadeiros.
Contradição --> É uma proposição composta em que todos seus valores são "F"alsos.
Contingência --> É uma proposição residual, ou seja, não é tautologia nem contradição; apresenta V e F em sua tabela verdade.
Bom, para aquelas pessoas que não "decoraram" nenhuma relação tautológica, só restaria em qualquer hipótese a construção da tabela verdade para cada assertiva.

a) P ∨ ¬ Q

P  Q ¬Q      P V ¬Q    ( Como se nota a valoração "F" mesclada com "V" torna a assertiva uma contingência)
V  V    F        V
V  F   V           V
F   V   F        F
F    F  V          V

b) P ^ ¬Q

P      Q   ¬Q         P^ ¬Q    Como se nota a valoração "F" mesclada com "V" torna a assertiva uma contingência)
V      V      F          F
V      F       V         V
F      V       F         F
F      F       V         F

c) ~P ^ Q

P   Q     ¬P      ~P^ Q  Como se nota a valoração "F" mesclada com "V" torna a assertiva uma contingência)
V   V     F          F
V   F        F      F
F      V        V       V
F       F        V        F

d) P v ¬P

P           Q      ¬P           P v ¬P
V           V            F            V
V           F               F       V
F      V        V           V
F            F              V        V

Tendo em vista, a valoração V em toda resultante da proposição composta estamos diante de uma tautologia.
PRIMEIRO VC ELIMINA AS QUE TEM CONECTIVO (E)

DEPOIS FICA ENTRE DUAS:

TESTAS AS ALTERNATIVAS.

p v ~p = GABARITO = D
SER OU NÃO SER ES A QUESTÃO P ou ~ Q é uma tautologia
Para encontrar a tautologia, a dica é a seguinte: Começa testando "condicional" e "disjunção inclusiva", pois são os conectivos que apresentam as menores chances de dar Falso (há apenas uma combinação que dá falso p/ eles, ai basta começar testando justamente essa combinação - no caso da disjunção precisa de F+F, no caso de condicional precisa de V+F). Sabendo isso, não tem como levar mais de 10 segundos p/ fazer isso.
P v ~P é sempre tautologia.
Resposta: alternativa D.

Comentário do professor Joselias Silva no YouTube:

https://youtu.be/WLIZ7frydMI
Fazer e refazer até aprender. Depois vc pega o bizu com facilidade! Não esqueça da tabela..

A) p^~q
P q ~q p^~q
V V F F
V F V V
F V F F
F F V F

B) p^~p
P Q ~p p^~p
V V F F
V F F F
F V V F
F F V F

C)~p^q
P Q ~p ~p^q
V V F F
V F F F
F V V V
F F V F

D) pv~p
P Q ~p pv~p
V V F V
V F F V
F V V V
F F V V

E) p^~q
P Q ~q p^~q
V V F F
V F V V
F V F F
F F V F

Faça os exercícios evitando de olhar a tabela para que possa memorizar.

ID

1169617

Banca

VUNESP

Órgão

PC-SP

Ano

2014

Provas

VUNESP - 2014 - PC-SP - Investigador de Polícia

Disciplina

Raciocínio Lógico

Assuntos

Para a resolução das questões de números 84 e 85, considere a seguinte notação dos conectivos lógicos:

∧ para conjunção, ∨ para disjunção e ¬ para negação.

Considerando a proposição ¬(p ∨ q), assinale a alternativa que apresenta uma proposição que lhe seja equivalente.

Alternativas

¬ p∧ ¬ q

p ∨ q

¬ p ∨ q

¬ p

¬ q

Comentários

Duasproposições são equivalentes quando possuem a mesma tabela verdade. Então vamosà construção das tabelas verdades:

...

P	Q	~P	~Q	P V Q	~(P V Q)	~P ^ ~Q	P V Q	~P V Q
V	V	F	F	V	F	F	V	V
V	F	F	V	V	F	F	V	F
F	V	V	F	V	F	F	V	V
F	F	V	V	F	V	V	F	V

RESPOSTA: ALTERNATIVA "A"

Gabarito. A.
¬(p ∨ q) = ¬ p∧ ¬ q ou negação
¬(PvQ): ¬P^¬Q
P | Q | (PvQ) | ¬(PvQ) é equivalente: ¬P | ¬Q | ¬P ^ ¬Q
v | v | v | F f | f | F
v | f | v | F f | v | F
f | v | v | F v | f | F
f | f | f | V v | v | V
"A vida é combate, que os fracos abate, que os fortes, os bravos só pode exaltar"
A negação de uma disjunção é a seguinte:

~(p v q) = ~p ^ ~q

Outra equivalência lógica é a seguinte: ~~p = p

Assim, pode-se verificar que ~(p ∨ q) = ~p ^ ~q
Teoremas de De Morgan
¬ p∧ ¬ q
Livro de bruno villar pdf de raciocinio logico questões cespe .pdf
Letra A
Questão bem tranquila, neste caso só basta trocar o conector (v ou) por (^ e) e manter a mesta base.
¬(p ∨ q) = ¬ p∧ ¬ q ou negação
Nesta questão, apenas temos que lembrar que a negação de uma disjunção é a conjunção, desse modo:
¬ (p V q) = ¬ p∧ ¬ q.
A resposta correta é a letra A.
RESPOSTA ALTERNATIVA A

p q ¬p ¬q p ∨ q ¬(p ∨ q) ¬p ^ ¬q

V V F F V F F

V F F V V F F

F V V F V F F

F F V V F V V
Nesta questão, apenas temos que lembrar que a negação de uma disjunção é a conjunção, desse modo:
¬ (p V q) = ¬ p∧ ¬ q.
A resposta correta é a letra A.
Para que as proposições sejam equivalentes basta que suas tabelas verdade sejam iguais.
¬(p ∨ q) <-------> ~p ^ ~q ( Leis de Morgan)

Importante saber essa lei. Caso o candidato se esqueceu, poderíamos verificar a identidade dessas proposições compostas construindo a tabela verdade. Vamos lá

P   Q       P V Q     ~( P VQ)   ~P       ~Q      ~P ^ ~Q
V    V        V               F             F           F            F
V    F        V               F             F           V            F
F    V        V              F              V           F            F
F    F        F              V               V          V            V

De fato esta comprovada a Lei de Morgan
Para negar uma disjunção ( inclusiva) , nega-se as proposições simples individuais transformando- as em uma proposição única( composta) formando uma conjunção.
Gente alguem pode me ajudar? Eu sei oq e tautologia, mas quando vejo questao igual a essa nao tenho nocao de que exatamente pede para fazer! :/
josiane sabrina antes de fazer a equivalência resolva os parenteses da questão. ~( P VQ) = ~P ^ ~Q e depois é só buscar a equivalente.
Gabaritagem é na letra A = )
O valor que procuramos é FFFV
a) FFFV
b) VVVF
c) VFVV
d) FFVV
e) FVFV
Tudo que está no parentese deve ser negado, assim para ter a equivalência da disjunção usa-se a conjunção:
¬(p ∨ q) = ¬ p ∧ ¬ q
repete a primeira e inverte a segunda (com o conectivo)
Todo mundo resolveu a questão como se fosse para fazer a negação, mas o enunciado da pergunta está pedindo a equivalência. Fiquei na dúvida..
gente nao confundam equivalencia com negacao a resposta e letra A somente troca-se o conectivo e mantem a mesma base
vunesp é uma mãe!
Veja o vídeo que gravei com a resolução dessa questão:
https://youtu.be/DQcvjC2HxXM
Professor Ivan Chagas
Nao sabia que a negação trocava o conectivo tambem ~(p ou q ) = ~p e ~q.... eu pensei que ficava ~p ou ~q . ainda bem que a galera explica! vlwwww
LETRA A!

Quando a banca é boazinha e põe a resposta logo de cara. s2
Para mim, o examinador pediu equivalência o qual não tem em nenhuma alternativa, por exclusão fui na negação que era a única possível.
Não tem como errar essa. A única alternativa que tem o conectivo "E" é a letra a
Ainda não entendi essa questão. todo mundo trata como se fosse negação.
cleber batista

Duas proposições são logicamente equivalentes quando possuem tabelas verdade iguais:

~(p ∧ q) ≡ (~p ∨ ~q)
~(p v q) ≡ (~p ^ ~q)
A negação de V é Ʌ.

Para negar uma frase com ‘e’ (Ʌ), basta negar as duas sentenças (¬)

Gabarito: A
Questão era pra ter sido anulada, visto que o enunciado pede EQUIVALÊNCIA e não Negação.

Equivalência da proposição ¬(p ∨ q), seria p -> ¬q . ( Regra do NEYMAR - Nega a prImeira e mantém a segunda).

Bons Estudos !!!
não tem oque se falar em anulação ...

P Q PvQ ~PvQ ~P ~Q a) ~Pv~Q
V V V F   F F   F
V F V F   F V   F
F V V F   V F F
F F F V   V V V

DEU UMA TRABLHEIRA FAZER ESSE QUADRO ,, DE NADA <3
Nem sempre ter a palavra "equivalente", significa que ele busca a equivalência. Não há que se falar em anulação.

Bons Estudos
não entendi essa resposta
Vendo a galera questionar o por que de se ter resolvido por negaçao vou explicar matematicamente:

considerando que p e q são duas variáveis com valor numérico respectivo 5 e 10:

logo a prep é: ~(p ou q) = -(5 + 10) = (-5-10) = -15, a negaçao disso seria =>

(~)~(p ou q) = (-) - (5+10) = +(-5-10) = -15

sendo assim negando toda a equaçao temos uma resposta equivalente!
Na verdade basta resolver os parenteses para chegar na resposta.

~(p v q)

Resolver esse parenteses, significar negar tudo dentro dele, já que tem uma negativa fora dele. Então, a negação de "p v q", é:

~p ^ ~q

Uma vez resolvido os parenteses, agora basta encontrar nas alternativas, uma resposta equivalente. A alternativa a), traz exatamente a mesma proposição da questão com os parenteses resolvido, portanto ela é equivalente (proposições exatamente iguais, são também equivalentes, obviamente).

Por isso muitos, inclusive eu, achou estranho resolver a questão fazendo uma negação, sendo que a questão pede a equivalência. O fato é, que simplesmente foi resolvido o parenteses (e para resolver o parenteses, foi necessário fazer a negação).

O parenteses foi a pegadinha.
~P    ^     ~Q     =
F         F              F
F         V              F
V         F              F
V         V              V

P    v    Q      =                     ~ ( P v Q )       EQUIVALENTE      ~ P ∧ ~ Q
V         V            V                    F                              F
V          F           V                    F                             F
F          V            V                    F                             F
F         F            F                    V                              V

Observação...tive que entrar na VERSÃO ANTIGA do QC para poder COMENTAR desta forma.

O Qc poderia manter a forma de comentar igual a versão antiga, poxa!!!!
Para negar o conectivo "ou" é necessário trocá-lo pelo "e" e negar as duas proposições.
Eu resolvi assim:

¬(p ∨ q) = esta negando toda a sentença

logo ∨ => ou

para negar = vira e = ∧

única alternativa que aparece ∧ = (A)
GABARITO: LETRA A

A ¬ (CANTONEIRA) = negação (pode ser também representada por ~).
Uma frase equivalente a uma negação também será uma negação.
A negação de V é Ʌ.
Para negar uma frase com ‘e’ (Ʌ), basta negar as duas sentenças (¬).

Logo a negação de ¬(p ∨ q) teremos:

¬ p∧ ¬ q
P= F
Q= F
Mas ele não pediu equivalência ? Uai
CORRETA: LETRA A

~(P V Q) ≡ ~P Ʌ ~Q

Sem Deus eu não sou nada!!!
É só usar a Negação da equivalência do conectivo (ou,Disjunção) que será conectivo (E conjunção) e resolver a questão. uma questão simples que a galera complicou .
Essa equivalência vc usa pela lei de morgan, vc distribui a negação em toda a proposição e nega tbm o conectivo, lembrando que a lei de morgan só funciona quando quiser equivalência do E (^) e do OU (v).
Gab.: A
Nesse tipo de questão basta desenvolver a proposição
~(P v Q) = ~P ^ ~Q

Se fosse pra negar, o que não é o caso, ficaria:
~[~(P v Q)]
~[~P ^ ~Q]
P v Q
Essa questão está estranha, eu procurei a equivalencia como solicitado no enunciado, não achei e chutei na letra A
O ideal é saber a Lei de Morgan, mas se não souber, uma opção é fazer no "braço", pois a proposição é pequena.

A tabela verdade da proposição do enunciado ¬(p ∨ q) fica assim:
¬(V ∨ V) = ¬(V) = F
¬(V ∨ F) = ¬(V) = F
¬(F ∨ V) = ¬(V) = F
¬(F ∨ F) = ¬(F) = V

Agora, por estar pedindo uma equivalente, é só procurar uma tabela verdade igual nas alternativas.

Alternativa A. ¬ p ∧ ¬ q
¬(V) ∧ ¬(V) = F ∧ F = F
¬(V) ∧ ¬(F) = F ∧ V = F
¬(F) ∧ ¬(V) = V ∧ F = F
¬(F) ∧ ¬(F) = V ∧ V = V

Na primeira alternativa já está a resposta, mas mesmo assim segue o resultado da tabela verdade das outras alternativas para vocês compararem e verem o porquê estão erradas.

Alternativa B. p ∨ q
V ∨ V = V
V ∨ F = V
F ∨ V = V
F ∨ F = F

Alternativa C. ¬ p ∨ q
¬(V) ∨ V = F ∨ V = V
¬(V) ∨ F = F ∨ F = F
¬(F) ∨ V = V ∨ V = V
¬(F) ∨ F = V ∨ F = V

Alternativa D. ¬ p
¬(V) = F
¬(F) = V

Alternativa E. ¬ q
¬(V) = F
¬(F) = V
A questão pede uma equivalência não uma negação. E a resposta da questão é uma negação. Questão mal formulada.
Lei de morgan
NEGAÇÃO DE \/ É /\ SIMPLES ASSIM. LEI DE MORGAN!

ID

1207966

Banca

CESPE / CEBRASPE

Órgão

TJ-SE

Ano

2014

Provas

Disciplina

Raciocínio Lógico

Assuntos

Julgue os itens que se seguem, relacionados à lógica proposicional.

A sentença “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil” é uma proposição lógica simples.

Alternativas

Certo

Errado

Comentários

E - não é comentário. Fundamente sua resposta.
Está errado porque existem duas proposições ligadas pela conjunção e ^ . O reitor...estar contente com as politicas... à educação superior (proposição P), e com os rumos atuas...... (proposição Q) logo, a sentença é expressa por P^Q.
Aqui é um campo destinado aos que se interessam em colaborar com os colegas que estão em processo de aprendizagem. Colocar o gabarito não é necessário, pois o próprio site já o faz.

Boa sorte a todos nós.
Creio que a pessoa que colocou o primeiro comentário dizendo apenas que estava correto não teve o objetivo de explicar a questão, mas sim de informar o gabarito àqueles que não são assinantes e conferem o gabarito das questões olhando os comentários. Isso é válido, pois, mesmo se tratando de um valor relativamente baixo, não é acessível a todos.
Essa é a característica do CESPE: um sujeito com dois predicados, assim é uma lógica composta. A ^ B.
Item certo.
O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país. (p)

O reitor declarou estar contente com os rumos atuais do movimento estudantil. (q)
Ou seja: p ˄ q, como bem frisado pelo colega.
Inicialmente, achei esquisito esse modo de ver da banca: utilizar-se apenas de um verbo (expressão verbal, no caso) para dois complementos numa sentença, e admiti-la como composta.
todo mundo falou ,falou e não explicou nada...
P = "O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país"
conectivo = "e"
Q = "com os rumos atuais do movimento estudantil” é uma proposição lógica simples"

Logo, P ^ Q = proposição lógica COMPOSTA.
A sentença é composta, pois possui duas proposições.
Existem duas orações lógicas, porém, na segunda oração o verbo está implícito. Assim temos:
"O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país" 1ª proposição
"(o reitor declarou estar contente) com os rumos atuais do movimento estudantil” 2ª proposição
É utilizado o conectivo e "^" entre as duas proposições.
para ajudar a identificar eu troco o conectivo E por outro conectivo
affffffffff sempre erro isso
`Para facilitar : faça a pergunta ao verbo - Quem declarou?
Gabarito ERRADO
Lembrando que para o Cespe se vc tem dois sujeitos (sujeito composto) em uma proposição mas apenas UM predicado, nesse caso então teremos uma prop. simples. Ex.: Jose e André são policiais honestos. Diferente do que ocorre nessa questão.
Duas proposições ligadas pelo conectivo "e" (^)

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país.
E - (^)
O reitor declarou estar contente com aos rumos atuais do movimento estudantil.

Portanto assertiva ERRADA
NÃO são consideradas preposições:
- perguntas
- desejos
- ordens
- opiniões
- frases entre aspas
O reitor declarou estar contende com as políticas relacionadas à educação superior adotadas pelo governo (E DECLAROU ESTAR CONTENTE) com os rumos atuais do movimento estudantil.
Nota-se, na frase implicitamente demonstrada entre parênteses, a presença significativa do conectivo "e", representado pelo símbolo "^". Portanto, a questão está errada.
É uma proposição composta, e não simples, como diz a questão.
Entendi. é como se o 'declarou estar contente ' estivesse elíptico na segunda afirmação. Por isso considerou como proposição COMPOSTA.
Proposição composta - São aquelas que apresentam pelo menos um dos conectivos lógicos.

Logo, errada a questão.
Se Liga no Conectivo "e" já mata a questão
Quer dizer que "Eu gosto de maçã." é uma proposição simples e, "Eu gosto de maçã e abacate." é uma proposição composta?
Sim Welington, a oração "Eu gosto de maçã e abacate." é composta,
pensa assim, você pode atribuir valor falso ou verdadeiro para as duas afirmações.
Eu gosto de maça = Verdadeiro ou Falso.
e Abacate = Verdadeiro ou Falso.
Se você escrever a sentença de forma completa fica mais fácil identificar : Eu gosto de maça e gosto de abacate.
Além disso:
"Eu e meu amigo gostamos de maçã" é proposição simples
PROPOSIÇÃO COMPOSTA PQ APRESENTA DUAS IDÉIAS!!!
Prezados amigos,
Temos uma proposição composta pela Conjunção e (^):
P: "O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país".
Q: "O reitor declarou estar contente com os rumos atuais do movimento estudantil”.
Sabemos que uma proposição simples ou atômica, é aquela que apresenta apenas uma ideia.
A sentença “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E com os rumos atuais do movimento estudantil”, não apresenta apenas uma ideia, pois o reitor além de estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país, ele também está satisfeito com os rumos atuais do movimento estudantil, temos então mais de uma ideia, além de estar presente um operador lógico de conjunção “e”.

RESPOSTA: ERRADO
A proposição é composta.
1ª proposição: O reitor estar contente com as políticas relacionadas a educação superior adotadas pelo governo de seu pais.
2ª proposição: Com os rumos atuais do movimento estudantil.
então, é uma proposição composta do tipo: Proposição P E proposição Q (P ^ Q) - CONJUNÇÃO
O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil.
O problema está no "e" que acaba tornando a sentença uma proposição composta.
A "e" B-> Logo Proposição composta.
Lembrem-se:
Pra não esquecer é só lembrar que são proposições compostas as que são formadas por todos aqueles conectivos lógicos ("e"; "ou"; "ou...ou"; se...então"; "se, e somente se,...")
Faço assim e acerto.

Abraços!
Resposta :ERRADA

Proposição composta: Duas proposições simples (declarativas,afirmativa ou negativa), ligadas pela conjunção "e".
Resposta :ERRADA
Proposição composta: Duas proposições simples (declarativas,afirmativa ou negativa), ligadas pela conjunção "e"; "ou"; "ou...ou"; se...então"; "se, e somente se,..."
declarou estar contente com as políticas...''e'' com os rumos atuais do movimento estudantil
Duas proposições,logo, proposição composta.
Gabarito E
NADA A VER.
Quer dizer que '' com os rumos atuais do movimento estudantil'' E UMA PROPOSIÇÃO?
ERRADA!!!!!
(Pessoal, cuidado, tem um comentário muito bem votado que está dizendo que a questão está correta, mas não está!)

Como disseram os colegas, essa proposição é composta:
A: “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país"
B: “O reitor declarou estar contente com os rumos atuais do movimento estudantil”
(O reitor é o mesmo sujeito, mas tem duas afirmações relacionadas a ele, e ainda ligadas pela preposição E.)
“O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil” = A^B

Abraços!
O Guilherme Peres falou tudo! O verbo está implícito na segunda oração. Showw!!
Questão errada, cobrou português além de raciocínio lógico...

Zeugma verbal, ocultou a locução verbal que já tinha sido mencionada
São duas proposições:

P1. O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país.
P2. (O reitor declarou estar contente) com os rumos atuais do movimento estudantil.

Então (P1 ^ P2) = O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil.
Eu acho que declarações não podem ser preposições pelo simples fato de não serem passíveis de julgamento. As declarações são tidas, em princípio, como verdades, ou seja, são monovalentes, e não bivalentes como as preposições.
http://equipe-exclusiva.com.br/downloads/raciocinio_logico.pdf
composição simples - aquelas que vêm sozinhas, desacompanhadas de outras proposições.
EX.: todo homem é mortal.
O novo papa é argentino.
todavia, se duas ou mais proporçoes vêm conectadas entre si (com conectivos "e, ou, se então, se e somente se, ou ou"), formando uma só sentença, estaremos diante de uma proposição composta.
EX.: João é medico e Pedro é dentista.
FONTE: Prof. Thiago Pacífico
logo o gabarito é ERRADO, pelo fato de se tratar de uma proposição logica composta
Gabarito: Errado

Resolução da Questão:
Julgue os itens que se seguem, relacionados à lógica proposicional.

A sentença “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil” é uma proposição lógica simples.

Conjunção: p ^ q (p e q)

Codificando a questão:

P: O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país;

Q: com os rumos atuais do movimento estudantil. Trata-se de uma proposição composta (uma conjunção) P ^ Q.

Visite: https://www.facebook.com/concurseironinja
Se ele está contente com duas coisas, logo COMPOSTA!
Ir pra o lado mas fácil : Que reitor ? Errei por ñ prestar atenção nisso ai! Afffzzzz Cespe viu? run'
Uma proposição simples é aquela em que apresenta somente uma ideia.
Ex 1 : Eu sou inteligente (Sujeito + verbo de ligação + predicativo) ideia com sentido único, sem necessidade de conectivo.
Só usamos um conectivo para unir ideias distintas.
Ex 2: Eu sou inteligente e rica, significa dizer que são duas frases separadas com sentidos independentes (Eu sou inteligente / Eu sou rica) e, por conveniência foram unidas. Para que ocorra a união é obrigatório a presença do conectivo "E", que tem a mesma função que uma conjunção tem no português, responsável por ligar orações.
Quando ocorrer um único sujeito apresentando mais de uma ideia estas ligadas por meio de conectivos estamos falando de uma proposição composta e NÃO SIMPLES.

GABARITO ERRADO.
Pensei que para ser composta , na outra proposição necessariamente teria que ter um verbo. mas se tiver duas ideias distintas sempre será composto?
Elas podem ser desmembradas em duas proposições e ainda farão sentidos:
A) O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país.
b) O reitor declarou estar contente com os rumos atuais do movimento estudantil.
Proposições compostas.
Uai! pensei que tinha Filtrado por "Raciocínio Lógico" cabo respondendo questões de Português! kkk
Acertei, mas não porque tem lógica e sim porque entendi: o Reitor está feliz com a Política e "Também" está feliz com movimento estudantil... faço como se em prova estivesse... acertaria a questão mas não concordo de isso aí ser R. Lógico.
E sim uma interpretação de texto advinda de algum texto anterior. Fato!
Cometário objetivo
Tem conectivo ( e = ^) é composto !
Gabarito ERRADO
POIS É KARINA, ATENTEM GALERA... O CONECTIVO "E" NÃO É QUALIDADE SUFICIENTE PARA DIZER SE UMA PROPOSIÇÃO É SIMPLES OU COMPOSTA.

EX: Maria e João estudaram muito.

NO ENTANTO, HÁ CASOS EM QUE A FRASE PARECE SER SIMPLES....E TEM O "E" ( coincidência ser essa questão ..rsrs ) AI TU TENS QUE OLHAR BEM PRO SENTIDO DA PROPOSIÇÃO, E VER SE ELA PODE SER DIVIDIDA...SE SIM... ABRAÇO: É COMPOSTA.

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E o reitor declarou estar contente com os rumos atuais do movimento estudantil.

--> PROPOSIÇÃO COMPOSTA

GABARITO "ERRADO"
Podemos representar essa proposição assim: p ^ q
Errado.
É uma proposição composta, ligada pelo conectivo E = ^

Bons estudos ! ;)
Pode parecer um absurdo, mas para mim todos estão apenas concordando com o gabarito. Ou seja, se a CESPE apresentasse o gabarito como "Certo", todos iriam concordar e apresentar soluções mirabolantes.
Parece que tem o conectivo E, mas depois do conectivo não vejo nenhum verbo. Por isso acho que é uma proposição simples.
A banca CESPE utiliza como objeto principal de estudo o predicado. Por isso, não é necessário ter dois sujeitos para ser composto.
A questão Q368660
Considerando os conectivos lógicos usuais e que as letras maiúsculas representem proposições lógicas simples, julgue o item seguinte acerca da lógica proposicional.A sentença “Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União, das Autarquias e das Fundações Públicas Federais” é uma proposição lógica composta.
Se usássemos o raciocínio comentada por quase todos aqui poderíamos dizer que essa questão Q368660 seria composta, pois, poderíamos dizer que está implícita:
P: Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos Servidores Civis da União,
Q: Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único dos das Autarquias
R: Os candidatos aprovados e nomeados estarão subordinados ao Regime Jurídico Único das Fundações Públicas Federais
Sendo assim teríamos P^Q^R^.
Acontece que no gabarito a questão está ERRADA ou seja ela é SIMPLES! E agora meus caros??? Alguém tem uma justificativa plausível para essa questão do CESPE? Simplesmente dizer que P, Q e R tem um mesmo sentido, pra mim seria forçar o gabarito!

Alguém consegue explicar a diferença entre a presente questão e essa outra aqui?

Q336543 - Ano: 2013 - Banca: CESPE - Órgão: TCE-RO - Prova: Auditor de Controle Externo - Direito

As pessoas têm o direito ao livre pensar e à liberdade de expressão - é uma proposição lógica simples.

Gabarito: certo
Mirandes, o que determina quantas proposições simples existem em uma sentença é a quantidade de verbos, que estará "separando" essas proposições com um dos conectivos lógicos.
Ex 1: Ana comprou (verbo) arroz e feijão => Proposição simples Ex 2: Ana comprou (verbo) arroz e (conectivo lógico) Maria, (a vírgula neste caso está "omitindo" o verbo) feijão. => Proposição composta. Espero ter ajudado. :)
só tem um problema no caso dessa questão não tem virgula alguma explique no caso dessa questão
Mirandes, a diferença está na arbitrariedade do examinador da CESPE, que ora diz que este tipo de construção é proposição simples e ora diz que é proposição composta.

Esse tipo de questão com um suposto conectivo "E" ligando duas supostas proposições simples é que me dá mais medo, pois o examinador não sedimenta um entendimento apenas, ele fica oscilando. Triste. O que nos resta é rezar pra não encarar uma destas na prova.

Abraço e bons estudos.
ERRADA
pelo fato de ser uma proposição lógica composta
“O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil”

Espero ter ajudado.
Bons estudos!
Nossa caí na pegadinha...rsrs mas da próxima acerto!
Fé em Deus que dar certo!
George Fontenelle,
Nesse caso, especificamente, discordo de vc, pois não existe um Regime Jurídico Único pra cada um dos citados (servidores, autarquias e fundações), é um mesmo para todos.
Ex: "Fui contratado para trabalhar na firma de advocacia Martins, Pereira e Silva". Isso não quer dizer que fui contratado para 3 firmas diferentes, apenas que aquela é comum (pertence) aos 3.
------------------------------------
Voltando para esta questão, particularmente, está bem complicada. É mais uma questão de interpretação, já que o verbo não está explícito:
"O reitor declarou estar contente com A e com B".
1) O reitor declarou isso e aquilo. - proposição simples
2) O reitor declarou estar contente com isso e contente com aquilo. - proposição (simples, acho)?????
3) O reitor declarou estar contente com isso e estar contente com aquilo. - proposição (simples, acho)?????
4) O reitor declarou estar contente com isso e declarou estar contente com aquilo - proposição composta
-----------------------------------
Qual exatamente o termo que devemos entender como implícito? Questões da CESPE ora apontam como simples, ora como composta. Alguém com melhor entendimento para esclarecer?
Gabarito: Errado

Trata-se de uma proposição composta pelo conectivo E. (P^Q)
Na minha humilde opinião a questão está com o gabarito errado,pois não há verbo depois da conjunção E,logo é uma proposição simples,inclusive já vi outras questões bem parecidas com essa serem consideradas como simples também.
"O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país..." O reitor declarou estar contente... com os rumos atuais do movimento estudantil" são duas ideias, entao é proposiçao logica composta.
GABARITO: ERRADO.

P = a ^ b

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país. (a)
O reitor declarou estar contente com os rumos atuais do movimento estudantil. (b)

Logo, é uma proposição lógica composta!!!

BOA MADRUGADA DE ESTUDOS!
Amanda, se você desmembrar a frase ficaria assim: O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e; O reitor declarou estar contente com os rumos atuais do movimento estudantil. Então há 2 verbos. é que não precisa repetir tudo de novo se você já colocou o conectivo.
P ^ Q ele está contente com uma coisa E outra

proposição composta ligadas pelo conectivo E
gabarito errado
O reitor DECLAROU estar contente com duas coisas. Essa também pode ser interpretada como uma proposição simples. Proposição indiscutivelmente composta seria " O reitor ESTÁ contente com A e com B". CESPE *%#%@*¨&!
O reitor declara que está contente com as políticas do governo e os rumos do movimento estudantil.

Políticas do governo e rumos do movimento estudantil são coisas completamente distintas, são duas ideias, duas proposições. Portanto, proposição composta.

Observe que "o movimento estudantil" não está complementando o sentido de "políticas do governo". O governo não faz movimento estudantil.
“O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país(um assunto) e com os rumos atuais do movimento estudantil”(outro assunto) ... PREPOSIÇÃO COMPOSTA " P^Q"

Resposta :ERRADA
Vou dá uma opção para o CESPE abrir um cursinho de interpretação, já pensou como iria vender?
O verbo está oculto (elíptico) na segunda oração "e estar contente com os rumos atuais do movimento estudantil."
A conjunção "e" faz a função de substituição do verbo "declarou", evitando-se a repetição desnecessária do mesmo.
A frase ficaria assim: O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e; o reitor declarou estar contente com os rumos atuais do movimento estudantil.
Duas orações na questão. Proposição composta. Raciocínio lógico intimamente ligado à Língua Portuguesa hehe.
Abraços!
Jesus... o povo viaja muito. Proposição composta ligada pelo conectivo "e", simplesmente.
quer me foder me beija, cespe.
Pelo que pude observar em questões Cespe, desenvolvi um macete para proposições:

- Sujeito composto e 1 predicado: Proposição simples
Ex: João e Maria tiveram um filho que lhes dava orgulho.
- Sujeite simples/composto e + de 1 predicado: Proposição composta
Ex: “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e {declarou estar contente} com os rumos atuais do movimento estudantil”
Uma pegadinha essa elipse!
Pessoal, estou com uma dúvida. Sei que quando emito opinião própria não é uma proposição, porque não posso valorar em V ou F. Minha dúvida é, se um terceiro emite opinião pode ser uma proposição? Pois para mim o reitor declarou a sua opinião, dizendo estar contente... Alguém saberia me responder essa dúvida, por favor? Considerei errada a questão, porque no início achei que fosse composta, mas me veio essa dúvida!
Diogo Oliveira! Não importa se é uma opinião! A questão não quer saber valores lógicos, mas sim se é proposição simples ou composta. Ou seja, questão desse tipo, é saber diferenciar proposição simples e composta.

Espero ter ajudado!
proposição é uma oração DECLARATIVA acho que isso responde sua pergunta
não podendo ser aberta, nem imperativa ou exclamativa.
Ele está contente com uma coisa E outra. ERRADO
A proposição “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E com os rumos atuais do movimento estudantil” é composta, porque podemos identificar o conectivo lógico de ligação E.
Por isso, gabarito: errado.
P^Q, onde:
P - O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país
(e)
Q - com os rumos atuais do movimento estudantil
Boa sorte!
Questao casca de banana, errei mas concordei com o gabarito, foi omitido o verbo na segunda proposição:

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E o reitor declarou estar contente com os rumos atuais do movimento estudantil.
Tentando explicar a dúvida do Mirandes

depois de errar várias questões desse mesmo tipo, cheguei a conclusão que a questão em tela é considerada composta pois completa o verbo e a questão proposta pelo mirandes não completa o verbo e sim um nome (o direito), vejam:
O reitor declarou isso(estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país) e declarou isso (com os rumos atuais do movimento estudantil)”
no outro caso, as pessoas só tem uma coisa o direito o restante é só complemento.
As pessoas têm isso (o direito) ao livre pensar e à liberdade de expressão - é uma proposição lógica simples.
Gabarito: certo
Dois pensamentos. Pronto.
Pessoal, resolvendo diversas questões do Cespe sobre isso, pude chegar à seguinte conclusão:
Se na proposição há 2 SUJEITOS e 1 PREDICADO --> Proposição SIMPLES.
Ex: Pauline e Tamara são servidoras públicas.

Se a proposição trouxer 2 VERBOS com ideia de UNICIDADE --> Proposição SIMPLES.
Ex: Pauline trabalha em uma autarquia federal ao mesmo tempo que ministra aulas em uma Universidade.

Se na proposição há 1 SUJEITO e 2 PREDICADOS --> Proposição COMPOSTA
Ex: Pauline declarou estar descontente com o serviço público e com o rumo atual da economia brasileira.
Se a proposição trouxer 2 VERBOS sem ideia de UNICIDADE --> Proposição COMPOSTA
"com os rumos atuais do movimento estudantil." não é uma proposição lógica simples, pois não é possível atribuir valor lógico à mesma.
A forma correta de apresentar as proposições seria: A = "O reitor declarou estar contente com as políticas relacionadasà educação superior adotadas pelo seu país." e B = "O reitor declarou estar contente com os rumos atuais do movimento estudantil."
Temos duas proposições (às quais eu posso atribuir valor lógico distinto para cada uma) que unidas pelo conectivo "E" se tornam uma proposição lógica composta.
Gabarito: ERRADO.

Declarou duas coisas sobre um único objeto. Logo, é proposição composta.
Bons estudos.
achou o conectivo? pronto acabou é composta
elison, não é bem assim "achou o conectivo? pronto acabou é composta".

Por ex.: Mariana e José são flamenguistas.
E ai, tem conectivo. É composta?? Não

É necessário observar a ideia da proposição, verificar se ocorreu zeugma de verbo (caso da questão)...enfim, para saber se de fato é uma composta temos que analisar a proposição se possui duas ou mais ideias que podemos valorá-las.
Não é apenas ver se tem conectivo, principalmente se for uma conjunção.
Galera bora parar de falar com tanta certeza as coisas, pois além de prejudicar a si (devido às explicações não serem tão certas assim), ainda prejudica ao próximo que usa os comentários como material de estudo.
Proposições com múltiplos verbos como "vim, vi, venci", mostram que existem mais de uma frase, porém estão implícitas. Também podemos ter zeugma de verbos, nos passando uma tremenda impressão de ser uma proposição simples. Para saber quantas proposições existem no exemplo dado entre aspas, é necessário mais do que decoreba. Se pudermos valorá-las, atribuindo "verdade" ou "falsa" em cada uma das orações, então tratar-se-á de uma proposição composta.

Vamos fragmentar as orações e após isso, tentar valorá-las.

Vejamos os exemplos abaixo:

1º EXEMPLO: "Vim, vi, venci"
1ª Oração: Eu vim -> Eu não vim.
2ª Oração: Eu vi -> Eu não vi
3ª Oração: Eu venci -> Eu não venci
É uma proposição composta!

2º EXEMPLO: "Corri para a escola, para a casa e para o trabalho."
1ª Oração: Corri para a escola -> Não corri para a escola
2ª Oração: Corri para a casa -> Não corri para a casa
3ª Oração: Corri para o trabalho -> Não corri para o trabalho
É uma proposição composta!

Além dessas dicas, devemos atentar também para vírgulas e conectivos.

Creio ter conseguido ajudar a alguns.

POLÍCIA FEDERAL!
O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país (1)/ e com os rumos atuais do movimento estudantil(2)”

composta
Juro q tento entender a explicacão do Flávio Batista, q escreve isso em muitas questões...
Nunca entendo qual o critério que o CESPE usa para essas questões.
“O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e (^)com os rumos atuais do movimento estudantil”
Proposição composta
O professor inventou uma regra ? Engraçado que em umas questões isso não tá certo por que dizem que deve ter mais de um verbo pra definir uma proposição composta. Assim fica difícil.
"com os rumos..." e "...com as políticas..." são complementos nominais de contente.
Estar contente é uma oração subordinada substantiva objetiva direta, que se relaciona ao verbo declarou.
As orações de lógica relacionam-se aos verbos, sendo assim "com os rumos" completa a palavra contente (novamente, complemento nominal), bem como o sintagma "...com as política"...
Incorreto pensar que "com os rumos..." liga-se diretamente ao verbo declarar, e pior se relacioná-lo ao "estar" que, apesar de ausente a conjunção "que", inicia a OSSOD.
Língua portuguesa e Matemática andam juntas. Fala-se que os alunos não sabem interpretar as questões, mas como ignorar essa análise?

Gostaria de um posicionamento mais forte.
Para a CESPE:

Pedro e José são altos. - proposição simples
Pedro é alto e José é alto. - proposição composta

O significado é o mesmo, então precisamos contar as orações.
Às vezes a banca deixa o verbo elíptico para dificultar um pouco, como no caso desta questão.
O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e
O reitor declarou estar contente com os rumos atuais do movimento estudantil = 2 orações ligadas pelo conectivo E
A e B = Proposição Composta
Gabarito: ERRADO
Para o cespe:
dois sujeitos e um verbo = prepo simples
Dois "complementos" e um verbo = prep composta
Esse examinador é um trogloditas, isso é um absurdo!!!

Separando as proposições não temos como julgá-la como verdadeira ou falsa, aliás, nem temos duas proposições aqui. E essa história de: vamos contar quantos verbos tem e dizer o número de preposições não serve para todas as questões.

01

Q402654

Raciocínio Lógico

Fundamentos de Lógica

Ano: 2014

Banca: CESPE

Órgão: TJ-SE

Prova: Técnico Judiciário - Área Judiciária

Resolvi certo

Julgue os itens que se seguem, relacionados à lógica proposicional.

A sentença “O sistema judiciário igualitário e imparcial promove o amplo direito de defesa do réu ao mesmo tempo que assegura uma atuação investigativa completa por parte da promotoria” é uma proposição lógica composta.

SE CONTAR O NÚMERO DE VERBOS AQUI NESSA QUESTÃO VOCÊ VAI ERRAR FEIO, FICA A DICA!

BONS ESTUDOS!!!
Continuo não concordando com os comentários sobre a questão que afirmam a resposta da banca. Como no meu comentário anterior disse, o que seria a segunda proposição ( e dita por muitos aqui como "complemento do verbo", o que é errado) é um complemento nominal de "contente", e permaneço com a minha resposta: proposição simples.

Esta maneira que o professor do site resolveu é simplista e ignora a sintática.
Não concordo com o gabarito

O que define ser uma proposição é poder valorar entre verdadeiro e falso, pois bem, vamos tentar fazer isso nessa assertiva de forma independente.

Vamos tentar a primeira: “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país" ok, podemos valorar, então é proposição.

Vamos tentar a segunda: "Com os rumos atuais do movimento estudantil” nao consigo valorar, alguem ai sabe dizer se é verdadeiro ou falso?

Uma vergonha essa banca, lamentável.
William Souza, o seu problema está no português.

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e (O reitor declarou estar contente) com os rumos atuais do movimento estudantil.

Não é necessário repetir o trecho em negrito e, inclusive, é recomendável não repetí-lo para que o texto não fique redundante.
Eu li os 79 comentários desta questão de de outras semelhantes que, a exemplo dessa, têm seus 79 comentários. A conclusão:

=> 2/3 somente ampliam o gabarito, INDEPENDENTEMENTE do resultado. Quer dizer, se o gabarito fosse CERTO, os mesmos 2/3 opinariam concordando (não acrescenta nada a ninguém).

=> O restante, que já se ligou, encontra divergências de gabarito para questões com os mesmos argumentos e comandos. Quer dizer, quando estamos diante de uma proposição com "e" ( ^ ), fora o caso dos dois sujeitos para um predicado e o caso dos dois verbos diferentes, é um DEUS NOS ACUDA. Não dá para adivinhar.

Parabéns Mirandes Pinheiro, Marcelo Cardoso, Hugo Nagaya e outros que raciocinam muito bem a lógica, porém notaram a lógica que não tem em algumas questões que da CESPE vem.

Para esses guerreiros e para os outros 2/3, me ajudem com essa então:

Q373856 - A sentença: “Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão {( P ^ Q ) ^ R}, em que P, Q e R sejam proposições convenientemente escolhidas. (ERRADO)

Q336543 - As pessoas têm o direito ao livre pensar e à liberdade de expressão - é uma proposição lógica simples. (CERTO)
sinceramente, nao sei qual o critério dessa banca!!! já fiz algumas questões dessa mesma Cespe e o gabarito era correto, considerando tais proposições como simples!
Isso não é uma proposição composta galera
Essa Cespe não é de Deus!
Podem dizer que é mimimi mas não é, eu considero que essa questão do CESPE é quase obrigatório pular pois apesar de ser algo, em tese, elementar na disciplina, a banca complica demais pois ela não é nem um pouco consistente em sua história quanto ao que ela considera proposição simples ou composta, é só ver algumas questões postadas por amigos, em que ela considera uma proposição com a mesma estrutura que essa da questão uma proposição simples
Sem critério nenhum...mais seguro deixar em branco na hora da prova :(
Errada

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e o reitor declarou estar contente com os rumos atuais do movimento estudantil.
Há duas ações: 2 Verbos Ligados pela conjunção E
P = O reitor declarou estar contente com as políticas relacionadas à educação superior .

Q = O reitor declarou estar contente com os rumos atuais do movimento estudantil.

Observação : São ideias distintas

Logo, P^Q é uma proposição composta.

GAB - ERRADO
PARA A BANCA CESPE 1 OBJETO + 2 DECLARAÇÕES = DECLARAÇÃO COMPOSTA
1 OBJETO: o reitor
1º DECLARAÇÃO: declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país
2º DECLARAÇÃO: declarou estar contente com os rumos atuais do movimento estudantil

Fonte: professor Jairo Teixeira (CERS).
Boa noite , alguém poderia me explicar por que a questão em tela foi considerada uma proposição composta e esta questão abaixo foi considerada simples??? Obrigada

Q373856 A sentença: “Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão (P∧Q)∧ R, em que P, Q e R sejam proposições convenientemente escolhidas.

Gabarito: Errado
Áurea, boa noite!

Apesar dos pesares, no que se refere à questão que vc postou aqui abaixo, acho que temos uma única idéia( após a vírgula) e por isso foi considerada preposição simples. É como se esses vários "e" ai estivesse unindo uma coisa só e não idéias diferentes

Vou tentar te exemplificar:

O cachorro amarelo e cinza saiu. - Note que o "e" seve apenas para ligar uma característica total do cachorro( ele é amarelo e cinza)

O cachorro saiu e entrou - Note que aqui há duas ações distintas feitas pelo mesmo sujeito!

Agora vendo sua questão:

Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão (P∧Q)∧ R, em que P, Q e R sejam proposições convenientemente escolhidas.

Note que seriedade, celeridade, sistema punitivo é como se formassem uma coisa só, como se fossem uma única característica( como o amarelo e cinza do cachorro que citei no exemplo!)

Bem, não sou muito didático para ensinar, mas espero que tenha ajudado!

Abraços!
A partir dessa questão, CESPE começou a dar defeito em RLM!
Áurea, se vc observar o início da proposição perceberá que há uma "enumeração", neste caso n é considerado proposição composta..

Ex.. Camila precisou de estudar, tirar notas boas e alcançar a média para passar de ano.
Mais uma questão que tenho que prestar a atenção 5x antes de responder.

Rídicula de tão fácil que o professor precisou comentá-la 2x.
O segundo "com" também é regência de "estar contente" assim percebe-se que são suas orações, portanto, proposição composta!
Cespe é incoerente. Em questões de 2015 eles considerariam essa afirmação como proposição simples...
Cada hora é uma coisa...acho q ela coloca esse tipo de questão pra ninguem gabaritar a prova
Que coisa feia, isso tudo é medo de alguém conseguir a proeza de gabaritar? Rsrsr
Se as políticas relacionadas à educação superior adotadas pelo governo de seu país e os rumos atuais do movimento estudantil é uma proposição lógica simples, então o rei fica contente.

(P^Q) -> R

Não é uma proposição simples, mas sim composta.

Lembrando que estadudar RML nã é como estudar para português.
GALERA ENCONTRA EXPLICAÇÃO PRA TUDO, ATÉ PARA UMA QUESTÃO ABSURDA COMO ESTA.

ALGUNS SE ADAPTAM AO GABARITO DA BANCA.
"Julgue os itens que se seguem, relacionados à lógica proposicional.
A sentença “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E com os rumos atuais do movimento estudantil” é uma proposição lógica simples."
ERRADO

Em minha opinião, a proposição é composta pois possui duas ideias:

1) O reitor DECLAROU ESTAR contente com as políticas relacionadas à educação superior adotadas pelo governo superior de seu país

E (conectivo)

2) O reitor DECLAROU ESTAR (implícito) contente com os rumos atuais do movimento estudantil

Dessa maneira, duas ideias, um conectivo (E), dois verbos, na verdade 2 locuções verbais (DECLAROU ESTAR, a do nº2 implícita), duas orações = proposição composta!
Como todos alunos do QC eu também solicitei os comentários de RL em vídeo. O Professor Vinicus tem uma didática super difícil e além de tudo o comentário por escrito torna a matéria mais complicada ainda.
RL é o tipo de matéria que certas explicações tem que ser através de desenhos e outros artifícios para que possa ser compreendida.

Pessoal façam o que eu fiz: no comentário do professor clique em "não gostei"; vai abrir um campo para o comentário; coloquem suas crítticas e solicitem as aulas em vídeo.

Obs; Não gosto de expor níguém, mas já perdi as contas de quantos vídeos já procurei no youtube para entender certas questões. E quando não encontro vídeo são os comentários dos colegas que fazem toda diferença. Não adianta somente solicitar os vídeos aqui nos comentários, pois acredito que não tem uma pessoa responsável no QC para ficar lendo os nossos comentários!

A partir de hoje vou colocar essa mensagem em todas as questões de RL....kkkk

Persistência!
Galera quando vier verbo implícito após o conectivo "e" desconsiderem esse conectivo. Em grande maioria das questões CESPE ele considera uma questão como essa como "proposição simples". Infelizmente é CESPE sendo CESPE.... Essa foi a única que deram como "composta" que eu vi até hoje. Claro, estou falando apenas de questões semelhantes a essa (com verbo implícito)... Mas ao meu ver, a regra geral do cespe é "verbo implícito após o conectivo "e" leva-se em considerção como proposição simples".
Errado

Eu entendi assim

1ºproposição:

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país.

2ºproposição;

O reitor declarou estar contente com os rumos atuais do movimento estudantil.
Isso é uma putaria. Quando a gente estuda uma coisa, é outra. Quando a gente estuda a outra, já não é mais.

Aprendi que para ser composta tem de ter verbo em cada uma das preposições, o que não é o caso aqui. Há apenas um verbo = declarou.
CESPE, SUA FILHA DA PUTA!!! ASSIM NAO TEM COMO TE DEFENDER!!!!!!! EXPLIQUEM ESSA ATEUS!!! Q373856 #NOJODESSABANCA
Tem duas afirmativas:

O reitor declarou estar contente:

1-Com as politicas relacionadas à educação superior, adotadas pelo governo do seu país;

2-Com os rumos atuais do movimento estudantil.

Duas proposições!!! Então a proposição é composta! Acho q é isso!
considerou o verbo " estar",,que estava implicito na segunda setença......passivel de anulação com certeza
Gente , presta atenção :

Se fossemos dividir essa frase , teriamos DUAS proposições , olhem o conectivo E ( Conjunção ) .

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E com os rumos atuais do movimento estudantil” é uma proposição lógica simples.

1º Proposição :

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país.

2º Proposição :

com os rumos atuais do movimento estudantil.

Pegadinha do Mução !!!
Não é lógica simples.... é a conjunção "e"
oui poderia pensar o seguinte:

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país

E

O reitor declarou estar contente com os rumos atuais do movimento estudantil
cespe é incoerente [2], em algumas questões considera esse tipo de frase como prop simples.

fora que se o que se considera como uma proposição é a quantidade de verbos, igual costumam dizer por aí, o trecho "com os rumos atuais do mov estudantil" não poderia ser outra proposição pq é referente à palavra "contente" ("contente com ... e com..." - complemento nominal). Já vimos complementos DOS VERBOS não serem considerados proposições e agora isso. É de cair o cu da bunda. Entraria com recurso com certeza
As proposições simples são as que indicam um fato singular (uno) ou que são singulares (unas) em virtude de uma conjunção. proposições múltiplas ou compostas são as que indicam não unidade, mas multiplicidade, ou que apresentam suas partes sem conjunção. (Fonte: Aristoteles, - Órganon, pg. 85).

A banca CESPE, quando a frase tem dois sujeitos e o mesmo predicado, a considera como sendo uma proposição simples. (Fonte: Bruno Villar - Raciocinio Lógico Facilitado , pg 21, 4ª ed.)

2 sujeitos ligados pelo "e" e 1 predicado = proposição simples.

1 sujeito comum e 2 predicados distintos = proposição composta

Nesta questão não houve uma relação de unicidade (predicado comum).
(P) O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país (^)e (Q)com os rumos atuais do movimento estudantil
ERRADO.

Existe a conjunção e(^) na proposição, então ela será composta.
CACETAAAAAAAAAAAAAADA!!!!! 4x errada

Vi claramente 2 ideias, mesmo assim pensei, isso não é o conectivo, é simples ¬¬

GAB ERRADO
Deem uma olhada nesta questão Q402654, é a mesma idéia só que com gabaritos diferentes, por isto odeio Cespe e RL , pois não tem lógica nenhuma esta porcaria de matéria. O professor vai pela onda da banca, perfeito o conhecimento dele da matéria.....
A Cespe vem cobrando Português nas provas de Lógica.

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil” é uma proposição lógica simples.

Quem é o sujeito? O Reitor

O Reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e,

O Reitor declarou está também contente com os rumos atuais do movimento estudantil

Logo uma proposição composta, gabarito ERRADO

Agora analisando outra questão Q373856

A sentença: “Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão , em que P, Q e R sejam proposições convenientemente escolhidas

Quem que é o Sujeito?? Um governo

Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão.

Percebam que o "e" está ligando complementos de tribunais e não do sujeito "Um governo". Gabarit: ERRADO

bom, pelo menos consegui resolver as questões com esse entendimento, caso esteja errado avisem-me.
Já cansei de ver questões deste tipo com gabaritos diferentes. Ou seja, não dá pra saber o que fazer, a banca dá o gabarito de acordo com o seu entendimento.

Eu duvido que todos acertaram questões deste tipo de primeira.
Não sei como interpretar essas questões. Em certas questões, um verbo só é classificado como proposição simples, em outras é composta. Tá difícil!
Eu não entendo a Banca CESPE, cada hora ela tem um entendimento sobre proposições simples ou compostas.

Aí a gente estuda, cai uma bosta dessa na prova e vc SABE A MATÉRIA mas, não sabe o que a banaca quer pois, em algumas provas entende de um jeito e em outras entende de outro.
Trata-se de uma frase trazendo 1 sujeito com mais de 1 predicado, com ideias diferentes. Para o cespe, sempre que isso acontecer, a proposição é composta.

Simplificando a frase:

O REITOR ESTÁ CONTENTE (COM AS POLÍTICAS EDUCACIONAIS) E (COM O MOVIMENTO ESTUDANTIL).

p1: O REITOR ESTÁ CONTENTE COM AS POLÍTICAS EDUCACIONAIS

p2: O REITOR ESTÁ CONTENTE COM O MOVIMENTO ESTUDANTIL

GAB: ERRADO.
Não entendi...

O verbo na segunda parte da proposição esta implícito e mesmo assim é considerado?
Tem-se que reescrever a frase buscando o sujeito da sentença. ― "do réu ao mesmo tempo que assegura uma atuação investigativa completa por parte da promotoria" Reescreva: Ao réu O sistema judiciário igualitário e imparcial promove o amplo direito de defesa, ao réu é assegura uma atuação investigativa completa por parte da promotoria. Veja que ambos orações referem-se ao mesmo sujeito, então a sentença é simples.

Vamos a outro exemplo: "A crença em uma justiça divina, imparcial, incorruptível e infalível é lenitivo para muitos que desconhecem os caminhos para a busca de seus direitos, assegurados na Constituição". Para muitos é lenitivo a crença em uma justiça divina, imparcial, incorruptível e infalível, muitos desconhecem a busca de seus direitos, para muitos serão assegurados na Constituição.

Veja que os argumentos prestam deferência ao sujeito.

Agora ―"O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil" "Os rumos atuais do movimento estudantil" é uma inferência absolutamente independente do reitor, isoladamente não se chega ao sujeito da oração de deferência, surge a necessidade de se usar um conectivo para conferir valor semântico a oração.
Vai entender o Cesp.

Julgue os itens que se seguem, relacionados à lógica proposicional.

A sentença “O sistema judiciário igualitário e imparcial promove o amplo direito de defesa do réu ao mesmo tempo que assegura uma atuação investigativa completa por parte da promotoria” é uma proposição lógica composta.

GAB: ERRADO

Julgue o item abaixo, relacionado à lógica proposicional.

A sentença: “Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão , em que P, Q e R sejam proposições convenientemente escolhidas.

GAB: ERRADO
Olá pessoal,

Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/ukA4hzHNoa0

Professor Ivan Chagas
www.gurudamatematica.com.br
Sujeito está elíptico na inserção da conjunção aditiva e.
CESPE, contratem um profissional de exatas para elaboração de provas de raciocíno L. e não um professor de português.
ERRADA

Acabei errando por fazer rápido, mas vejam:

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e ( estar contente) com os rumos atuais do movimento estudantil

É o verbo que está subentendido. Chamamos isso de Elipse.

Exemplo: Eu venho cedo e você, tarde.
Podemos entender: Eu venho cedo e você vem tarde.
FICO COM MUITO ÓDIO DESSES COMENTARIOS, SO P PUXAR SACO E DIZER QUE É INTELIGENTE

(Ano: 2013 Banca: CESPE Órgão: TCE-RO Prova: Auditor de Controle Externo - Direito)
As pessoas têm o direito ao livre pensar e à liberdade de expressão - é uma proposição lógica simples

GABARITO CORRETO

A BANCA DECIDI QUAL GABARITO ELA ESCOLHE
Gabarito:ERRADO

O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país e com os rumos atuais do movimento estudantil = composta

Outra que ajuda a entender:
O sistema judiciário igualitário e imparcial promove o amplo direito de defesa do réu ao mesmo tempo que assegura uma atuação investigativa completa por parte da promotoria. = simples
GAB ERRADO

Essas questão de SIMPLES ou COMPOSTA que na hora da prova está duvidosa é melhor deixar em braco, já que uma hora cespe tem uma posição correta outra hora não. Mas enfim, a banca escolhe o gabarito dela, num é...

CESPE sendo CESPE
O reitor declarou estar contente com isso E com aquilo.

Item: Errado.

Bons estudos.
Q336543 - A P2 - As pessoas têm o direito ao livre pensar e à liberdade de expressão - é uma proposição lógica simples. Certo
Se aparecer na proposição: 'ou'; 'ou, ou'; 'se, então'; 'se, e somente, se'; é composta. Agora, se aparecer 'e', somente será composta se vier dois verbos explícitos na proposição. Se vier um verbo só, é simples. 'Que' e 'Para' anulam o verbo posterior a deles, ou seja, não conta esse.
Para a banca CESPE:

Sujeito Composto + Um Predicado = Proposição Simples.
Ex.: João e Antonio são ótimos engenheiros.
Apenas um predicado.

Sujeito Simples + Dois ou mais Predicados = Proposição Composta.
Ex.: O diretor declarou estar contente com as notas dos alunos e com a responsabilidade dos professores
Locução verbal fica subentendida
O diretor declarou estar contente com as notas dos alunos [1]
E (declarou estar contente) com a responsabilidade dos professores [2]
Ano: 2015 Banca: Órgão: Provas:
Considerando que as proposições lógicas sejam representadas por letras maiúsculas e utilizando os conectivos lógicos usuais, julgue o item a seguir a respeito de lógica proposicional. A sentença “Somente por meio da educação, o homem pode crescer, amadurecer e desenvolver um sentimento de cidadania" pode ser simbolicamente representada pela expressão lógica P ∧ Q ∧ R, em que P, Q e R são proposições adequadamente escolhidas.

GABARITO ERRADO
Que loucuraaa! Ontem respondi uma com verbo elíptico errada... hoje certo! Deus Ajude!
O melhor de tudo é o comentário do professor:

Autor: Vinícius Werneck:
Sabemos que uma proposição simples ou atômica, é aquela que apresenta apenas uma ideia.
A sentença “O reitor declarou estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país E com os rumos atuais do movimento estudantil”, não apresenta apenas uma ideia, pois o reitor além de estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país, ele também está satisfeito com os rumos atuais do movimento estudantil, temos então mais de uma ideia, além de estar presente um operador lógico de conjunção “e”.

Já para esta outra questão:

A sentença: “Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso” pode ser corretamente representada pela expressão (P/\Q)/\R , em que P, Q e R sejam proposições convenientemente escolhidas. - Gabarito: Errado.

O MESMO professor (Vinícius Werneck) diz:

A sentença “Um governo efetivo precisa de regras rígidas, de tribunais que desempenhem suas funções com seriedade e celeridade e de um sistema punitivo rigoroso", não pode ser representada pela expressão ( P ^ Q) ^ R, em que P, Q e R sejam proposições convenientemente escolhidas, pois a mesma é uma proposição simples, que expressa um único raciocínio, ou um único pensamento.

kkkkkkkkkkkkkkkkkk muita palha assada.
Quem é esse Reitor? Onde fica seu país?
essa aqui é simples, segundo o Cespe no mesmo ano
“O sistema judiciário igualitário e imparcial promove o amplo direito de defesa do réu ao mesmo tempo que assegura uma atuação investigativa completa por parte da promotoria”
https://www.qconcursos.com/questoes-de-concursos/questoes/1f8e69cf-06
Estou farto dessas questões com conectivo "e", ora são ditas simples, ora compostas. Não vejo uma boa explicação para as classificações.
Só sei que nada sei.
A cada prova é utilizada uma jurisprudência Cespiana diferente.
O gabarito está incorreto, visto que NÃO HÁ 2 VERBOS EXPLÍCITOS juntamente ao conectivo "e".
que ridículo
que ridículo
GABARITO: ERRADO
Para se ter uma proposição composta, deve haver 2 verbos ou mais e eles não podem estar implícitos, porém, quando se trata do conecto OU, essa regra não é válida, ou seja, mesmo com verbo implícito, será composta
Ex: Sou vendedor e aluno (proposição simples)
Sou vendedor ou aluno (proposição composta)
Questão desatualizada!
https://www.estrategiaconcursos.com.br/blog/cespe-anula-questao-polemica-de-raciocinio-logico-no-concurso-da-pf/
Interessante fazer a leitura pra entender o entendimento atual da banca
Não sabia que raciocínio lógico iria me ajudar em redação! hahaha gostei!
• 1ª etapa: análise da sentença:
• sentença: o reitor declarou estar contente com as políticas relacionadas à
educação superior adotadas pelo governo de seu país e com os rumos atuais
do movimento estudantil.
• A = o reitor declarou estar contente com as políticas relacionadas à educação
superior adotadas pelo governo de seu país;
• “∧” = “e”;
• B = com os rumos atuais do movimento estudantil;
• sentença = A∧B.
• 2ª etapa: análise final:
Portanto, a sentença “O reitor declarou estar contente com as políticas relacionadas
à educação superior adotadas pelo governo de seu país e com os rumos atuais do
movimento estudantil” é uma proposição lógica composta. Desse modo, a questão
encontra-se errada.
GABARITO: ERRADO

O reitor além de estar contente com as políticas relacionadas à educação superior adotadas pelo governo de seu país, ele também está satisfeito com os rumos atuais do movimento estudantil, temos então mais de uma ideia, além de estar presente um operador lógico de conjunção “e”.

ID

1223467

Banca

IBFC

Órgão

EBSERH

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Se o valor lógico de uma proposição p é verdadeiro e o valor lógico de uma proposição q é falso então o valor lógico da proposição composta [(p → q) v ~ p ] ^ ~ q é :

Alternativas

Falso e verdadeiro

Verdadeiro

Falso

Inconclusivo

Comentários

Temos:[(p-->q) v ~p] ^ ~q, onde p=Verdadeirae q=Falsa. Resolvendo de pedaço :), temos:
p--> q, substituindo fica: V --> F = F
p --> q v~p, substituindo fica: F v F(se p=V, ~p=F) = F
p --> q v ~p ^ ~q, substituindo fica: F^ V (se q= F, ~q=V) = F
Logo,o valor lógico da proposição composta é Falso
Gabarito:Letra C
Se o valor lógico de uma proposição p é verdadeiro e o valor lógico de uma proposição q é falso então o valor lógico da proposição composta [(p → q) v ~ p ] ^ ~ q é :

[(p →   q)    v ~ p ]    ^ ~ q
      (V ---> F) v F] ^ V
=   (F v F) ^ V
= F ^ V = F
De acordo com o enunciado, "p" é V e "q" é F, assim pela Tabela-Verdade da Condicional, Disjunção e da Conjunção:

[(p → q) v ~ p ] ^ ~ q = [(V → F) v ~ V ] ^ ~ F = [F v F ] ^ V = F ^ V = F

Resposta: Alternativa C.
Nesta questão alguém poderia me dizer se dá para resolver com a tabela verdade e se sim poderia mostrar como faz, porque estou fazendo, mas está dando erro.
resolvi desta maneira!
[(p → q) v ~ p ] ^ ~ q:
[F v F] ^ ~ q
F ^ F
F
logo: gabarito letra C
Se o valor lógico de uma proposição p é verdadeiro e o valor lógico de uma proposição q é falso então o valor lógico da proposição composta.

---> (CONDICIONAL) SE, ENTÃO: Não precisa resolver. Questão para perder tempo!

P=V

Q=F

V ---> F = F
Gabarito: C

[(P -> Q) v (~P)] ^(~Q)]

[(V -> F) v F ] ^ V ]

[ F v F ] ^ V

F ^ V

F
Vera Fischer é FALSA, usei só essa frase pra fazer a resolução!

ID

1232845

Banca

CESPE / CEBRASPE

Órgão

SUFRAMA

Ano

2014

Provas

CESPE / CEBRASPE - 2014 - SUFRAMA - Nível Médio - Conhecimentos Básicos - Todos os Cargos

Disciplina

Raciocínio Lógico

Assuntos

Considere as seguintes proposições:

P1: Se o Brasil reduzir as formalidades burocráticas e o nível de desconfiança nas instituições públicas, eliminar obstáculos de infraestrutura e as ineficiências no trânsito de mercadorias e ampliar a publicação de informações envolvendo exportação e importação, então o Brasil reduzirá o custo do comércio exterior.

P2: Se o Brasil reduzir o custo do comércio exterior, aumentará o fluxo de trocas bilaterais com outros países.

C: Se o Brasil reduzir o nível de desconfiança nas instituições públicas, aumentará o fluxo de trocas bilaterais com outros países.

A partir dessas proposições, julgue o item seguinte a respeito de lógica sentencial.

Se a proposição C e a proposição “O Brasil aumentou o fluxo de trocas bilaterais com outros países” forem verdadeiras, então a proposição “O Brasil reduziu o nível de desconfiança nas instituições públicas” também será verdadeira.

Alternativas

Certo

Errado

Comentários

se A então B = v
nesse caso se B for verdadeiro então A poderá ser V/F
gab: errado
Errado.

"também será verdadeira." Não necessariamente será verdadeira.
P-->Q só será falso se for V e F, logo P pode ser V ou F, o valor da proposição vai depender também de Q.

Espero ter ajudado.
Pessoal, a questão fala que ambas proporções são verdadeiras, digo a proporção C e a proporção dada na questão. Não entendi o porquê do gabarito. Podem esclarecer?
Proposição C É uma condicional = P --> Q
A banca fala que a Proposição C é verdadeira. Ora, sabemos que no condicional para ser F a primeira tem que ser V e segunda F. Mas como a banca disse que a proposição é V, então podemos ter os seguinte valores:
V e V = V
F e F = V
F e V = V
Em todas o resultado será verdadeiro.
Proposição P2 é uma condicional P --> Q, e a banca afirmou que "aumentará o fluxo de trocas bilaterais com outros países" é V.
Já vimos que para ser verdadeira há três possibilidades. Então não podemos afirmar que "O Brasil reduziu o nível de desconfiança nas instituições públicas" é também V pois pode admitir tambem o valor de F.

Repetição com Correção até a Exaustão, Leva a Perfeição.
Lamartine Melo,

A assertiva diz que a proposição C como um todo é verdadeira e que a 2ª parte dela (aumentará o fluxo de trocas bilaterais com outros países) também é verdadeira. Logo, tanto faz 1ª parte ser V ou F que a proposição sempre será verdadeira, pois só é falsa se a 1ªV e a 2ªF.

Gabarito: E, pois a 1ª parte pode ser V ou F.

Espero ter ajudado.
Se todos os comentários, como os da Juliana Carvalho, fossem baseados em esclarecer os pontos obscuros da mente dos indoutos como eu, todos aprenderiam muito mais.

Apenas complementando para ajudar a resolver a questão, e não somente ensinando lógica:

O comando da questão trouxe a proposição “O Brasil reduziu o nível de desconfiança nas instituições públicas”. Essa proposição só existe na C. Além disso, a consequência da C o comando já disse que é verdadeiro (aí precisa um pouquinho de raciocínio lógico). Pronto! Questão resolvida.

Isso quer dizer que não há necessidade de se preocupar com as proposições anteriores, porque elas NÃO vão influenciar a resposta da questão e vão exigir do candidato muito tempo e esgotamento mental na hora da prova.

Espero ter ido além do "mais do mesmo" e ajudado os colegas. Força!
Não necessariamente .... “O Brasil reduziu o nível de desconfiança nas instituições públicas” pode ser V ou F

já que é uma condicional temos V/F -> V = V
Gente, vejam se estou certo:
(C^P) ----> ~p

V F

* Considerei a frase "Brasil aumentou" como P e "Brasil Reduziu" como ~P

Então cheguei no resultado acima.
No "Se... Então" quando a INFO2 for Verdadeira, e o valor lógico da sentença como um todo tiver que ser Verdadeira, qualquer valor (VouF) que for inserido na INFO1, continuará sempre sendo verdadeira essa sentença.

Questão dada.
Estou com o comentário de Juliana Carvalho! ;)
A proposição C é representada por P-->Q

Com C(V): P(Fou V)-->Q(V) temos que P tanto pode ser falso quanto verdadeiro que ambos tornarão a sentença verdadeira, logo podem fazer a tabela e conferir.

Errada
ERRADO

BEM SIMPLES

QUAL CONECTIVO? CONDICIONAL(SE...ENTÃO)

*PROPOSICÃO C SERÁ VERDADEIRA SEGUNDO A QUESTÃO.

*A SEGUNDA PARTE DA PROPOSIÇÃO SERÁ VERDADEIRA TAMBÉM.

C: Se o Brasil reduzir o nível de desconfiança nas instituições públicas, aumentará o fluxo de trocas bilaterais com outros países. = V

P (?) -------> Q (V)

QUAIS AS POSSIBILIDADES DE VALORES LÓGICOS?

P-->Q = V

V V = V

F V = V

DEU PARA PERCEBER QUE A PRIMEIRA PARTE(P) TANTO VAI PODER TER VALOR (F) COMO (V),ENTÃO NÃO DAR PARA AFIRMAR SEU VALOR LÓGICO.
Errada

"o Brasil reduzir o nível de desconfiança nas instituições pública" poderá ser tanto V como F.
SIMPLES! O tempo verbal não influi em nada na lógica proposicional, eles só mudam o tempo para confundir o candidato. Por isso vou empregar os verbos no infinitivo impessoal.

C: Se o Brasil reduzir o nível de desconfiança nas instituições públicas, aumentará o fluxo de trocas bilaterais com outros países.

A: O Brasil reduz o nível de desconfiança nas intituições públicas

B: O Brasil aumenta o fluxo de trocas bilateriais com outros países

C: A --> B

C: F --> V [V]

C: V --> V [V]

Ora, se B for VERDADE, A não vai ser NECESSARIAMENTE VERDADE. Veja as possibilidades acima.
O nosso problema é que o gabarito oficial considerou essa questão como certa e a banca não reconsiderou, o que a gente pode fazer numa situação dessas?
PESSOAL UMA DICA: SÓ FAZER O MÉTODO DA CONCLUSÃO "FALSA"!

Eu sempre tive dificuldades com esse tipo de questão, mas depois que aprendi o método nunca mais errei! Vai na fé! =)

Vc falsifica a conclusão “O Brasil reduziu o nível de desconfiança nas instituições públicas” (F), depois vc coloca todas as premissas como (V), faça o teste: 1) Se caso as premissas continuarem V mesmo depois da conclusão F, então a conclusão/proposição em "xeque" será FALSA (INVÁLIDA). 2) Se pelo menos umas das premissas ficarem F, com a conlusão F, então a conclusão/proposição em "xeque" será VERDADEIRA (VÁLIDA).

No caso acima deu FALSA/INVÁLIDA.

GABARITO: ERRADO

Espero ter ajudado alguém!
Não se esqueçam de ler o texto associado! Talvez as confusões nesta questão tenham surgido por falta de ler o texto.

1º) Quem é C? C é "Se o Brasil reduzir o nível de desconfiança nas instituições públicas, aumentará o fluxo de trocas bilaterais com outros países." É uma condicional com resultado VERDADEIRO, de acordo com o enunciado.

2º) Se a premissa "aumentará o fluxo de trocas bilaterais com outros países" é VERDADEIRO.

3º) logo, "Se o Brasil reduzir o nível de desconfiança nas instituições públicas" poderá ser VERDADEIRO ou FALSO.

Gabarito então está errado, pois só considerou o verdadeiro.
ERRADO

BEM SIMPLES

QUAL CONECTIVO? CONDICIONAL(SE...ENTÃO)

*PROPOSICÃO C  SERÁ VERDADEIRA SEGUNDO A QUESTÃO.

*A SEGUNDA PARTE DA PROPOSIÇÃO SERÁ VERDADEIRA TAMBÉM.

C: Se o Brasil reduzir o nível de desconfiança nas instituições públicas, aumentará o fluxo de trocas bilaterais com outros países. = V

   P (?) -------> Q (V)

QUAIS AS POSSIBILIDADES DE VALORES LÓGICOS?

P-->Q = V

V   V = V

F   V = V

DEU PARA PERCEBER QUE A PRIMEIRA PARTE(P) TANTO VAI PODER TER VALOR (F) COMO (V),ENTÃO NÃO DAR PARA AFIRMAR SEU VALOR LÓGICO.
Pode ser tanto verdadeiro como falso
Resumindo:

Ele afirma que a proposição C é verdadeira:

C: Se o Brasil reduzir o nível de desconfiança nas instituições públicas, aumentará o fluxo de trocas bilaterais com outros países. V

Existem 3 possibilidades da proposição condicional ser verdadeira:

V V = V

F V = V

F F = V

Portanto, não necessariamente, “O Brasil reduziu o nível de desconfiança nas instituições públicas” também será verdadeira. Pois existe a possibilidade dela ser falsa.
Rd -> Af = V

f/v v Não se pode concluir o valor da primeira proposição.
GABARITO ERRADO.

Sempre quando surgir essas questões de RLM afirmando algo sempre tente quebrar o que o item afirma.

A--->B: Se o Brasil reduzir o custo de desconfiança nas instituições públicas,(então) aumentará o fluxo de trocas bilaterais com outros países. A--->B = F--->V = VERDADEIRO.
B: O Brasil aumentou o fluxo de trocas bilaterais com outros países. B = VERDADEIRO.
A: O Brasil reduziu o nível de desconfiança nas instituições públicas. A = FALSO.

Quebrei a ideia.
Vemos que tem a possibilidade da primeira proposição composta ser VERDADEIRA e a outra FALSA.
Se estudo então passo.
A pessoa pode não estudar e mesmo assim passar, seila no chute.(seria bom ne, quem nunca fez uma prova so no chute kk)

então a primeira é F e a segunda é V
a segunda nao influencia o valor lógico da primeira, apenas o valor lógico da sentença.
NAO NECESSARIAMENTE...NO CONECTIVO SE ENTAO

O PRECEDENTE PODE VIM VERDADEIRO OU FALSO

CASO ELE VENHA FALSO...PODE JOGAR COMO VERDADEIRO,POIS A UNICA FORMA DE SER FALSO É

NO VERA FICHE.
num entendi nada, deu proposição C, considerei a p%#$ da proposição C completa
igor menndes A proposição "O Brasil reduziu o nível de desconfiança nas instituições públicas" não garante a verdade da proposição completa.

Já a proposição "O Brasil aumentou o fluxo de trocas bilaterais com outros países” tem valor V, ou seja, ela garante a veracidade da proposição completa.
Minha contribuição.

Tabela verdade da condicional / Se..., então... / -> :

V -> V = V
V -> F = F
F -> V = V
F -> F = V

Abraço!!!
Gabarito: Errado.

A questão só garantiu que o consequente das proposições é verdadeiro. No entanto, isso não garante que, por si só, o antecedente também seja. Se, em uma estrutura condicional, o consequente é verdadeiro, o antecedente pode ser verdadeiro ou falso, fato que tornará a proposição completa sempre verdadeira - visto que uma condicional só passa a ser falsa se o antecedente for verdadeiro e o consequente for falso.

Diante disso, não há como afirmar que a proposição “O Brasil reduziu o nível de desconfiança nas instituições públicas” também será verdadeira.

Bons estudos!
com essa conclusão é possível que "C" seja Vera Fisher rs...

portanto ERRADO
Só observar a tabela da condicional (se então)
Quando o antecedente for F, independente dos próximos valores o resultado será V.
Quando o consequente for V, independente dos valores do antecedente o resultado será V.

P → Q
V → V = V
V → F = F
F → V = V
F → F = V
O consequente sendo verdadeiro garante que a proposição seja verdadeira, mas mesmo assim não é possível saber o valor do antecedente, pois ela será verdadeira de qualquer forma, ademais, por não ter uma certeza o gabarito é errado.
Comando: Se a proposição C e a proposição [Q] forem verdadeiras [...]
[P] Se o Brasil reduzir o nível de desconfiança nas instituições públicas, [Q] aumentará o fluxo de trocas bilaterais com outros países.
F -> V = V
V -> V = V
Gab. Errado, porque independente dos valores na proposição [P] o resultado será V.
se o consequente for VERDADEIRO, o antecedente pode tanto ser VERDADEIRO, como FALSO

ID

1232851

Banca

CESPE / CEBRASPE

Órgão

SUFRAMA

Ano

2014

Provas

CESPE / CEBRASPE - 2014 - SUFRAMA - Nível Médio - Conhecimentos Básicos - Todos os Cargos

Disciplina

Raciocínio Lógico

Assuntos

Se a proposição “O Brasil reduziu o custo do comércio exterior” for verdadeira, então a proposição P1 também será verdadeira, independentemente do valor lógico das demais proposições simples que constituem a proposição P1.

Alternativas

Certo

Errado

Comentários

Certo!
Uma proposição condicional só pode ser falta se a 1ª for verdadeida e a 2ª falsa, nos demais casos a proposição vai ser verdadeira.
Assim:
V -> F = F
V -> V = V
F -> V = V
F -> F = V
Na questão é informado que a 2ª é verdadera. Portanto nos dois casos em que a segunda tem valor V a proposição é válida, independente do valor da 1ª.
Espero ter ajudado.
Para nunca esquecer: Numa condicional, o único caso que torna a proposição falsa é a primeira verdadeira e a segunda falsa:
V -> F ( VERA FISCHER )
Se “O Brasil reduziu o custo do comércio exterior” for verdadeira não torna verdadeira a frase “O Brasil reduzirá o custo do comércio exterior”. Discordo com a resposta, devia estar errada.
Certa, no se então quando a posterior é V ela será verdadeira indepedente dos valores e conectivos na primeira parte da proposição.
P1 = "Se o Brasil reduzir as formalidades burocráticas e o nível de desconfiança nas instituições públicas E eliminar obstáculos de infraestrutura e as ineficiências no trânsito de mercadorias E ampliar a publicação de informações envolvendo exportação e importação, ENTÃO o Brasil reduzirá o custo do comércio exterior. " Temos uma premissa composta por quatro elementos aqui, representando A^B^C->D

O enunciado da questão disse que se a premissa “O Brasil reduziu o custo do comércio exterior” for Verdadeira, então independentemente do valor da outra premissa, o valor de P1 será verdadeiro.

Vemos que “O Brasil reduziu o custo do comércio exterior” equivale á premissa D, "Se o Brasil reduzir as formalidades burocráticas e o nível de desconfiança nas instituições públicas (A) E eliminar obstáculos de infraestrutura e as ineficiências no trânsito de mercadorias (B) E ampliar a publicação de informações envolvendo exportação e importação (C), ENTÃO o Brasil reduzirá o custo do comércio exterior. (D) "

A^B^C->D
A^B^C-> V
Para a condicional simples (->) ter valor negativo, a condição suficiente (elemento antes do conectivo) deverá ser verdadeiro e a condição necessária (elemento após o conectivo) deverá ser falso, ou seja, V->F.
Nesse caso, como o elemento após o coectivo (condição necessário) é V, consequentemente a premissa sempre será verdadeira independentemente se o valor do elemento anterior do conectivo (condição suficiente) for Falso ou Verdadeiro.
V->V = V
F->V = V
Assertiva Correta
Certa
Na tabela do "Se...Então..." quando a segunda proposição é "V", a primeira pode ser tanto "V" quanto "F";
A própria pergunta invalida a resposta cretina do professor para a questão anterior...Ele nem quis comentar essa aqui.
Acho que as premissas de P1 seriam assim:

P: O Brasil reduzir as formalidades burocráticas e o nível de desconfiança nas instituições públicas,

Q: Eliminar obstáculos de infraestrutura e as ineficiências no trânsito de mercadorias

R: Ampliar a publicação de informações envolvendo exportação e importação

S: O Brasil reduzirá o custo do comércio exterior.

P ^ Q ^ R - > S

Se S é verdadeiro, a proposição P1 será verdade para qualquer valor de P, Q e R
CORRETA

V/F -->V =V

--> OLHA A REGRA DO ( -->)

SÓ É ( F) ASSIM:

V-->F= F
Não precisa nem montar a expressão no papel. Na condicional, se depois do "então" for verdadeiro, não importa o valor das outras! Pode ter 10 premissas falsas, o resultado será sempre verdadeiro.

PS.: Regra da Vera Fisher é FALSA!
CORRETA

V/F -->V =V
Não precisa nem representar a expressão por letras. A questão fala que a segunda proposição na condicional é verdadeira, logo, se é uma condicional, o resultado será sempre verdadeiro. Na condiconal, é impossível um valor lógico falso tendo a segunda como verdadeira.

Na condicional o valor lógico só é falso da seguinte forma: V --> F = F ( Vamo Fazer um Filho)
Na condicional, o que importa é o valor da segunda proposição.
jogou verdadeiro na segunda frase AUTOMATICAMENTE NAO DARA

V F F

VERA FICHE É FALSA
CERTO

MODUS PONENS

huhuhu
P1: (Rf ^ Nd ^ Eo ^ It ^ AP) -> Rc

V/F V certo
GABARITO CORRETO.
O Brasil reduziu o custo do comércio exterior. VERDADEIRO.
P1: Se o Brasil reduzir as formalidades burocráticas e o nível de desconfiança nas instituições públicas, (e) eliminar obstáculos de infraestrutura e as ineficiências no trânsito de mercadorias e ampliar publicação de informações envolvendo exportação e importação, então o Brasil reduzirá o custo do comércio exterior.
?^?^?^?--->V = VERDADEIRO.
Pessoal na condicional sendo o último termo VERDADEIRO não me interessa os antecedentes, pois eles sendo falsos ou verdadeiros a conclusão sempre será verdadeira.
A^B^(C^D)^X--->Z = CERTA
Fazendo hj e errei por nao considerar a proposição simples do enunciado como integrante da P1 composta, que é complexa e cansativa, mas basta analisar o condicional e não precisa traduzir todas as simples. Se o consequente é verdadeiro, tanto faz se o antecedente é F ou V
O professor Luis Telles sempre fala:

se então (→):
_ (F) lamengo na frente sempre será VERDADEIRO e (V) asco atrás também sempre será VERDADEIRO.

o que não pode ocorrer é (V) asco na frente e (F) lamento atrás, pois sempre será FALSO.

Na questão ele informa que (V) asco ficará atrás, então independendo dos valores lógicos das outras sentenças ela será VERDADEIRA.

#PAZ
CORRETA

V/F -->V =V
Vasco em segundo é sempre V
Minha contribuição.

Tabela verdade da condicional / Se..., então.../ -> :

V -> V = V
V -> F = F
F -> V = V
F -> F = V

Abraço!!!
CERTO

P1 - Se o Brasil reduzir as formalidades burocráticas e o nível de desconfiança nas instituições públicas, eliminar obstáculos de infraestrutura e as ineficiências no trânsito de mercadorias e ampliar a publicação de informações envolvendo exportação e importação (V ou F), então o Brasil reduzirá o custo do comércio exterior. (V).

Sabemos que a preposição “O Brasil reduziu o custo do comércio exterior” é verdadeira. Portanto não importa se a preposição anterior terá valor de F ou V, pois o conectivo SE --> ENTÃO só é falso nos casos de V --> F (vera fisher).
Só observar a tabela da condicional (se então)

Quando o antecedente for F, independente dos próximos valores o resultado será V.
Quando o consequente for V, independente dos valores do antecedente o resultado será V.

P → Q
V → V = V
V → F = F
F → V = V
F → F = V
Se..., Então só pode ser falso com a Vera Fischer, logo então se o consequente for verdadeiro, não importa o valor do antecedente, será sempre V.
Se perguntar quantas proposições simples ou quantas linhas tem, o coro come!

ID

1241485

Banca

FCC

Órgão

TRF - 4ª REGIÃO

Ano

2014

Provas

FCC - 2014 - TRF - 4ª REGIÃO - Técnico Judiciário - Área Administrativa

Disciplina

Raciocínio Lógico

Assuntos

Considere verdadeiras as afirmativas:

Se não fui ao mercado, então não fiz compras.
Comprei creme e sabonete.
Ou comprei queijo ou comprei iogurte.
Comprei cereal ou comprei pão.

A partir dessas afirmações, pode-se concluir que

Alternativas

fui ao mercado e comprei sabonete.

não comprei nem queijo nem iogurte.

não fui ao mercado.

só comprei creme.

não comprei cereal nem pão.

Comentários

Análise Geral:

Da P2 temos que o indivíduo COMPROU CREME e COMPROU SABONETE. Então já concluímos que
FEZ COMPRAS, então “não fiz compras” é falso.
Da P1, como não fiz compras é Falso, então obriga que “não fui ao mercado” seja falso para deixar
verdadeira a premissa. Desta forma FOI AO MERCADO.
Nas premissas P3 e P4 não podemos precisar ao certo o que foi comprado.
Desta forma, analisando as alternativas, a única possível é a alternativa A, pois FOI AO MERCADO e
COMPROU SABONETE.
Letra A
Pessoal fiz da seguinte forma, me corrija se estiver errado, mas cheguei na conclusão
Primeiro tenho que calcular se todos as premissas são verdadeira para concluir se a premissa é validada ou falsa
f f = v
P1: Se não fui ao mercado -> não fiz compras Neste caso podemos afirmar que é Falsa mas F -> F = V
v
P2: Comprei creme e sabonete no segundo caso é uma preposição simples verdadeira
v F = V
P3: ou comprei queijo ou comprei iogurte já neste caso a primeira é verdadeiro e a segunda é falsa então se torna verdadeiro
Obs: Disjunção Exclusiva (v) ou...ou → V + V = F e F + F = F o restante é verdadeiro
v v = v
P4: comprei cereal V comprei pão aqui podemos também concluir que é verdadeiro V v V = V
-------------------------------------------
C: Fui ao mercado e comprei sabonete premissa VALIDO
A MEU VER A QUESTÃO FICOU SEM RESPOSTA.

para que P2 seja verdadeira o indivíduo tenha que comprar, obrigatoriamente, creme e sabonete.

Outro erro:
para que a P4 seja V, uma das duas opções tem de ser V.

A CONCLUSÃO proposta apresenta somente a compra do sabonete.

Deveria ter apresentado a opção de compras:
- creme, sabonete e pão; ou
- creme, sabonete e cereal.

Se me equivoquei no raciocínio, ajuda-me.
Se resolvermos apenas a segunda proposição teremos a resposta, nem é necessário olhar para as outras sentenças, vejamos:
"Comprei creme e sabonete." essa é única certeza que a questão nos dá, lembrando que essa proposição é uma conjunção e na conjunção para ser V as duas sentenças precisam ser V, então só nos resta a alternativa A
segue mais uma forma de fazer a questao, foi assim que consegui entender:
1) A sentença com "ou .. ou" é verdadeira quando possui símbolos diferentes, (VF / FV ), logo, podemos eliminar a alternativa B da questao, que nega as duas (nem queijo, nem iogurte.)
2) a sentença com "e" é verdadeira quando ambos os simbolos sao V ( VV), assim, eliminados a alternativa D , que afirma que somente o creme foi comprado, mas, para que seja verdadeira a sentença tem-se que comprar os 2 itens (creme e sabonete).
3) a sentença com "ou" para ser verdadeira basta 1 V ( VV, VF, FV) , o que torna a alternativa E errada, pois esta nega as duas opcoes (nem cereal, nem pao).
4) se vc perceber, verá que em todas as sentenças há possibilidade de se fazer alguma compra, logo elimina-se a alternativa C, restando como correta a alternativa A.
espero ter contribuido!
Se não fui ao mercado, então não fiz compras. Se só VF é falso: pode ser FF VV ou FV

Comprei creme e sabonete. Só VV é V logo, eliminada a D

Ou comprei queijo ou comprei iogurte. 1 ou outro já elimina letra B, e se comprei ou queijo ou igourte, não fiz compras é F e como a proposição tem que ser verdadeira a única forma é negar a primeira parte. Fui ao mercado C tbm eliminada

Comprei cereal ou comprei pão. Ou só FF é F, logo tenho de comprar um dos 2 letra E fora , sobrou a letra A
As premissas quando forem todas verdadeiras, você terá que começar com conjunção ou preposição simples...
Fiz dessa forma:
1.Se não fui ao mercado, então não fiz compras.
2.Comprei creme e sabonete.
3. Ou comprei queijo ou comprei iogurte.
4. Comprei cereal ou comprei pão.
são 4 proposições. comecei pela com "e" (proposição 2) porque Verdadeiro com Verdadeiro é igual a verdadeiro, assim 2.Comprei creme e sabonete. V V = V (V V = V)
Se comprei é porque fiz compras logo a segunda frase da proposição. sabe-se que VF é igual a falso, como a segunda frase é falsa a 1º terá de ser falsa também para que dê verdadeiro, assim 1.Se não fui ao mercado, então não fiz compras. F F = V (VF=F)
será verdadeiro Se fui ao mercado, então fiz compras. 3. Ou comprei queijo ou comprei iogurte. (VF= V , FV=V) uma é verdadeira e a outra é falsa
4. Comprei cereal ou comprei pão. (FF=F) pelo menos 1 é verdadeir
DAS RESPOSTAS SE PODE CONCLUIR
A. fui ao mercado e comprei sabonete.AMBAS SÃO VERDADEIRAS. É A RESPOSTA

B. não comprei nem queijo nem iogurte. ERRADO - um dos 2 foram comprados

c. não fui ao mercado. ERRADO porque foi ao mercado
d. só comprei creme ERRADO - comprou tanto creme quanto sabonete

e.não comprei cereal nem pão. ERRADO foi comprado pelo menos 1 deles
~M então ~C (v) - FF = V
Cc ^ S (v) -VV= V
Q v I (v) VV = V
Ce v P (v) VV = V
P (v) - Se comprei pão, logo fiz compras, parti do princípio que todos os demais itens foram comprados, pois no "ou", tanto faz VV ou V/F ou F/V
Alternativa A.
A segunda frase deixa claro de que ela comprou sabonete. Se ela comprou sabonete, então quer dizer que foi ao mercado.
Para que "comprar creme e sabonete" seja uma proposição verdadeira, comprar creme precisa ser verdadeiro e comprar sabonete tambem. A alternativa "A" diz que "fui ao mercado e comprei sabonete", então para ser verdade essa proposição "fui ao mercado" tbm e verdadeiro
Considere verdadeiras as afirmativas:

I. Se não fui ao mercado, então não fiz compras.
II. Comprei creme e sabonete.
III. Ou comprei queijo ou comprei iogurte.
IV. Comprei cereal ou comprei pão.

Ao analisar esta questão vc tem que partir da seguinte ideia: se vc foi ao mercado, vc comprou alguma coisa OU se vc não foi ao mercado, obviamente vc não pôde per comprado nada.
Veja: Partiremos do pressuposto de que todas as setenças são verdadeiras.
I. Se V, então V (opção que tornaria falso as demais(II, III e IV) sentenças) ou Se F, então (V ou F) para que seja verdade a sentença. É importante observar que a possibilidade Se F, então V apesar de verdadeira, não vai servir no nosso caso, pois inviabilizaria a veracidade de qualquer uma das demais sentenças, uma vez que todos os produtos são comprados no mercado ou assim deve ser entendido a meu ver. Portanto, se I. Se F, então F é verdadeira e exige a veracidade das demais;
II. V e V (Única possibilidade para ser verdadeira);
III. Ou F ou F / Ou V ou V (Possibilidades possiveis para que III seja verdade) ;
IV. V ou F / F ou V (Pssibilidades para que IV seja verdade).
A partir dessas afirmações, pode-se concluir que
A. fui ao mercado e comprei sabonete.
É possível. Pois a única possibilidade de II ser verdadeira e as duas serem verdade;
B. não comprei nem queijo nem iogurte.
Impossível. Pois analisamos acima que para as demais serem verdade, (I) deve ser Se F, entao F, sendo necessário assim comprar ao menos um elemento.
C. não fui ao mercado.
Impossível. Pois se não fosse ao mercado como compraria algum produto?
D. só comprei creme.
Impossível. Pois a sentença em que o creme está presente o conectivo usado é o E, exigindo-se assim que a outra proposição também seja verdade.
E. não comprei cereal nem pão.
Impossível. Pois para a sentença IV ser verdade é necessário que compre pelo menos o cereal ou o pão, mas não excluir os dois.
Perfeito, Raissa e Fabiana. :)
Lembrando que para a Raciocínio Lógico não importa a lógica, um gato pode voar, uma vaca pode tossir, cachorro tem chifre, etc.

Então uma pessoa pode fazer compras sem ir ao supermercado, o que tem de mais nisso? Logo não podemos deduzir isso, o correto seria analisarmos as proposição pelos seus valores lógico e não pela lógica, entenderam?
Concluindo, não consegui achar alternativa correta. Fiquei entre as letras a e c
p -> Q
Resolvi assim:
Começando pela disjunção exclusiva "Ou comprei queijo ou comprei iogurte. " Para que seja verdadeira, apenas uma das proposições deve sê-lo. Logo, se comprei ou queijo, ou iogurte, fiz compras.
Com esta conclusão, podemos afirmar que "então não fiz compras." da primeira afirmação está FALSA. Logo, "Se não fui ao mercado" também é FALSA. Pois em uma condicional, não podemos usar V->F sob pena de torná-la falsa. Consequentemente, podemos afirmar que "fui ao mercado" é VERDADEIRA.
Partindo para a segunda afirmativa: "Comprei creme e sabonete. " Para que seja verdadeira, na conjunção, todos devem ser verdadeiros. Logo, Comprei creme é VERDEDEIRA e (comprei) sabonete também é VERDADEIRA.
Por isso, podemos afirmar que FUI AO MERCADO e COMPREI SABONETE.
Minha forma de resolver (o enunciado afirma que são proposições VERDADEIRAS, logo, coloquei um "v" do lado de todas elas)

(f) (f)
Se não fui ao mercado, então não fiz compras. (v)

Comprei creme e sabonete. (v)
(?) (?)
Ou comprei queijo ou comprei iogurte. (v)

(v) (f)
Comprei cereal ou comprei pão. (v)

Então, chego a conclusão que:
FOI AO MERCADO
FEZ COMPRA
COMPROU CREME E SABONETE
COMPREI CEREAL
NÃO COMPREI PAO

RESULTADO:
Eliminamos de cara a "E", "D", "C"
A duvida seria entre "A" e "B". Por eliminação a correta é a letra "A"
1º Se não fui ao mercado, então não fiz compras. - proposição composta por condicional, verdadeira; lembrando que será falsa somente quando o antecedente verdadeiro e consequente falso. verdadeira para os demais casos com isso o antecedente poderá ser "V" ou "F". não é possível alguma conclusão em relação às alternativas.
2º Comprei creme e sabonete. - proposição simples verdadeira. logo elimina-se a alter. "d" e fica desconfiando da "a".
3º /Ou comprei queijo /ou comprei iogurte. - propos. composta por disjunção exclusiva, (verdadeira). portanto as duas simples possuem valores diferentes logo uma das duas verdadeira, com segurança, elimina-se a "b".
4º Comprei cereal /ou comprei pão. - propos. composta por disjunção inclusiva, (verdadeira). da mesma forma, uma das duas (propos. simples) é verdadeira. elimina-se a "e".
então com segurança a alternativa "a". pois não é possível concluir algo sobre a "c" o ler primeiro item.
Se não fui ao mercado, então não fiz compras. (V) --- F então F = V --- resposta A (fui ao mercado e comprei sabonete.)
Comprei creme e sabonete. (V) --- F e F = F
Ou comprei queijo ou comprei iogurte. (V) --- F ou,ou F = F
Comprei cereal ou comprei pão. (V) --- F ou F = F
Considerando as afirmativas verdadeiras, temos:

1) Começando com a conjunção:

Comprei creme e sabonete. ⇒ V ^ V = V

Logo, se comprei creme e sabonete são verdades, obrigatoriamente "não fui ao mercado" e "não fiz

compras" são falsos, assim:

2) Se não fui ao mercado, então não fiz compras. ⇒ F → F = V

As outras duas afirmações são disjunções, logo não temos como ter certeza sobre o valor lógico

das proposições simples que a compõe.

Assim, a única certeza que temos a partir da conjunção é que "fui ao mercado", "comprei

creme e sabonete" são verdades.

Letra A.
Ele comprou creme e sabonete
Então ele fez COMPRAS

Se ele fez Compras então ele foi ao MERCADO
só isso já elimina a "C" e a "D"
Ele comprou:ou queijo ou iogurte: então ele comprou só um dos dois: isso elimina a "B"
Ele comprou Cereal ou Pão: (pode ser os dois, ou um dos dois, mas jamais nenhum dos dois) eliminamos a "E"

Voltando ao raciocínio original.... Ele comprou creme e sabonete então ele fez compras; se ele fez compras ele foi ao mercado, Então "Ele foi ao mercado e comprou sabonete"
GAB:A
P1: Se não fui ao mercado, então não fiz compras.

P2: Comprei creme e sabonete.

P3: Ou comprei queijo ou comprei iogurte.

P4: Comprei cereal ou comprei pão.

A partir dessas afirmações, pode-se concluir que

(A) não comprei nem queijo nem iogurte.

Errado, pois a P3 diz que comprou um destes

(B) não fui ao mercado.

(C) só comprei creme.

Errado, pois a P2 diz que comprou creme e sabonete

(D) fui ao mercado e comprei sabonete.

(E) não comprei cereal nem pão

Errado, pois a P4 diz que comprou um destes

Análise Geral:

Da P2 temos que o indivíduo COMPROU CREME e COMPROU SABONETE. Então já concluímos que

FEZ COMPRAS, então “não fiz compras” é falso.

Da P1, como não fiz compras é Falso, então obriga que “não fui ao mercado” seja falso para deixar

verdadeira a premissa. Desta forma FOI AO MERCADO.

Nas premissas P3 e P4 não podemos precisar ao certo o que foi comprado.

Desta forma, analisando as alternativas, a única possível é a alternativa D, pois FOI AO MERCADO e

COMPROU SABONETE.
Respondi por eliminação.
Comprei creme e sabonete (conectivo "e", todas as proposições devem ser verdadeiras), logo, entendemos que "não fui ao mercado" e "não fiz compras", são proposições com valores lógicos falsos. A partir daí, fui respondendo as outras proposições e cheguei na letra "A" como resposta.
Se não fui ao mercado, então não fiz compras. P < - > Q - FF = V (Inverte a negação = Fui ao mercado)
Comprei creme e sabonete. P^Q - VV = V (ambas são verdadeiras, conector "e").
As demais estão ou erradas ou incompletas, aí fui de letra A
Considere verdadeiras as afirmativas:

Se não fui ao mercado, então não fiz compras.
Comprei creme e sabonete.
Ou comprei queijo ou comprei iogurte.
Comprei cereal ou comprei pão.
A única que dá pra começar dando valor lógico é a
Comprei creme e sabonete. (pois, como o enunciado diz q são verdadeiras, no conectivo E, pra ser V, os dois têm que ser V)
         V                      V
A partir disso, olhemos as outras. No OU OU não tem como sabermos pois não fala nada a respeito de queijo ou iogurte e, para ser verdade, apenas um tem que ser V pois o conectivo Ou Ou é excludente. Na ultima, mesma coisa, não temos como dar valor lógico pois o OU só será falso se ambos forem F. A unica q dá pra agregar valor lógico é a primeira
Se não fui ao mercado, então não fiz compras. (sabemos que fiz compras, pois comprou sabonete e creme, logo,
                                                   F       (não fiz compras fica F)
No Se Entao, se o consequente é falso, pra q a proposição toda seja verdade, o primeiro termo tem que ser F tbm, pois só será F se for VF
Se não fui ao mercado, então não fiz compras.
                F                              F
Então, a unica coisa que podemos afirmar é que EU FUI AO MERCADO, FIZ COMPRAS E COMPREI CREME E SABONETE.
Logo, alternativa A
a negação pode aparecer de maneira indireta. Comprar algo é o mesmo que negar não fiz compras.
QUESTÃO BEM SIMPLES. NÃO PRECISARIA NEM QUEBRAR A CABEÇA COM OS CONECTIVOS. POR ELIMINAÇÃO JÁ RESPONDERIA E GANHARIA TEMPO PARA AS OUTRAS QUESTÕES.
GABARITO: A.
Basta fazer a tabela-verdade das duas primeiras afirmativas:

Vejamos a primeira afirmativa: Se não fui ao mercado, então não fiz compras.
a) Fui ao mercado (V)
b) Fiz compras (V)
~a: não fui ao mercado (F)
~b: não fiz compras (F)
Pela tabela verdade da condicional, se ambas as proposições são falsas, a afirmativa pode ser verdadeira. Deduzimos, então, que fui ao mercado e fiz compras.
Vejamos a segunda afirmativa: Comprei creme e (comprei) sabonete.
c) comprei creme
d) comprei sabonete
Na conjunção, para que a afirmativa seja verdade, ambas as proposições devem ser verdadeiras, o que significa ser verdade que comprei creme e sabonete.
Desta forma, já sabemos ser verdade que "Fui ao mercado e comprei sabonete". Alternativa a está correta. Se quiser tirar a teima, é só ir adiante nas tabelas-verdade.
A
Devemos lembrar sempre que a lógica argumentativa trata da FORMA e não do CONTEÚDO.

Tem comentário concluíndo que, por ter comprado algo, é lógico que fez compras. Não é por ai. A primeira premissa poderia ser qualquer coisa, que se tornaria verdade; pois a equivalência de ~A --> ~B é B --> A (PURA FORMA).
Alternativa a) X
Acertei a questão, mas foi pela lógica das proposições e não pelo conteúdos das mesmas.
Fiquei na dúvida agora, pensei que não importasse a forma em si, ou seja, o fato dela der comprado o creme não significaria que ela teria ido ao supermercado.
Não é necessário nem a construção lógica, pois nesse caso temos premissas e toda premissa é verdadeiro e na conjunção para ser verdadeiro é necessário que ambas as proposições sejam verdadeiras, com isso podemos concluir NECESSARIAMENTE que: Comprei creme e sabonete, logo a partir dessa conclusão posso concluir outra que seria: fui ao mercado
Fui pelo mesmo raciocínio do comentário do professor...
O único que teríamos certeza é "Comprei creme e sabonete" devido ao conectivo "e".
À partir disso, se comprei creme e sabonete é porque fui ao mercado, então :

Fui ao mercado e comprei sabonete.
"À partir" não tem crase,partir é verbo só uma obs Caroline
devemos começar pela conjução E, pois é a unica que não tem outra opção se não V em todas as proposições da mesma.

apos isso, devemos atribuir valores que não sejam considerados Fnos valores dos conectivos, ai fica facil ver o resultado da pergunta.
Alternativa: A
A frase: Comprei creme e comprei sabão. Usa o conectivo "e" e para a frase ser verdade, tanto p= Comprei creme e q= Comprei Sabão tem que ser verdade.
Exemplo: (p= V ^ q= V) = V.
E como na questão não menciona nada sobre quais frases são verdadeiras, logo devemos pensar que todas são verdadeiras.
Na questão D menciona sobre creme, entretanto sabemos que não comprei apenas creme. Na primeira frase "Se não fui ao mercado, então não fiz compras" é p -> q =V , logo para isso ser verdade há inúmeras possibilidades, só não poder ser p=V e q=F pois desta maneira a frase seria F.
Logo, temos certeza que comprei creme e sabão= V e há possibilidade de ter não ter ido ao mercado ser tanto verdadeira como falsa.
eu vi
-comprei creme e sabonete = V
"Logo"
A) fui ao mercado e comprei sabonete - Lógica
Não perco mais tempo com questões deste tipo. :)
Bons estudos!
A equivalente ao Se então é o volta negando, ficando assim:

Se fiz compras, então fui ao mercado. Logo fui ao mercado.

Para que "Comprei creme e sabonete" seja verdadeira as 2 tem que ser verdadeiras. Logo comprei creme e sabonete.

Resposta letra A: fui ao mercado e comprei sabonete.
Professor podia comentar este tipo de questão em vídeo, ajudaria bastante entender.

#melhoraQC
o comentário do professor tem que ser em vídeo.
Comprei creme e sabonete

V V

logo fui ao mercado e fiz compras, comprando esses dois itens. ELIMINAMOS A ALTERNATIVA (c)

Elimino também a (d) porque se eu comprei já duas coisas, não posso dizer que SÓ comprei creme.

As outras duas proposições são com conectivo ou

Então, pelo menos um item de cada frase eu comprei (pq pelo menos um é verdadeiro). Elimino (b) e (e)

(a) Fui ao mercado e comprei sabonete
prestando bastante atenção. comprei queijo E sabonete ( V) é o ponto de partida dessa questão porque as duas preposições são verdadeiras

Não fiz compra será falsa, logo Não fui ao mercado também será falsa

~P então ~Q = F/F = Verdadeiro

Não fui ao mercado = F

Fui ao mercado = V

Comprei sabonete = V

Quando uma proposição é falsa sua negação é verdadeira
Nossa um dia atrás estava totalmente perdido com relação a RL(burrão mesmo), após assitir essas vídeo aulas https://www.youtube.com/watch?v=svq6rZW9ha4 deu pra ter uma noção e ja estou conseguindo resolver as questoes, essa por exemplo,resolví numa boa!
Resolvendo de forma lógica: Primeiro ele diz que não foi ao mercado e não fez compra, depois que comprou creme e sabonete, logo ele foi ao mercado.

GABARITO A

BONS ESTUDOS
Considerando as afirmativas verdadeiras, temos:

1) Começando com a conjunção:

Comprei creme e sabonete. ⇒ V ^ V = V

Logo, se comprei creme e sabonete são verdades, obrigatoriamente "não fui ao mercado" e "não fiz

compras" são falsos, assim:

2) Se não fui ao mercado, então não fiz compras. ⇒ F → F = V

As outras duas afirmações são disjunções, logo não temos como ter certeza sobre o valor lógico

das proposições simples que a compõe.

Assim, a única certeza que temos a partir da conjunção é que "fui ao mercado", "comprei

creme e sabonete" são verdades.

Letra A.

Fonte: QC
Com o perdão da palavra,algumas explicações dos colegas não tem nexo algum!Bem mais simples:primeiro ele fala que é para considerar todas as afirmações VERDADEIRAS.Começamos pela proposição que tem o conectivo "e",ela é V quando as duas forem V,com isso,comprei creme é V e comprei sabonete é V.Segundo vamos para a proposição se..então,usando a equivalência,nega,nega,troca,troca,fica: se fiz compras então fui ao mercado.Essa expressão é equivalente a "Se não fui ao mercado então não fiz compras",e como ele disse no começo,ela é V,logo sua equivalente também sera V.De posse dessas duas informações vemos que "fui ao mercado" e "comprei sabonete".Letra A é a resposta.
Se não fui ao supermercado, então não fiz compras.

EU FIZ compras, comprei: sabonete, creme, cereal e pão (certezas).

a) fui ao mercado e comprei sabonete (CERTO, fui ao supermercado e comprei sabonete - além de outras coisas) - GABARITO

b) não comprei nem queijo nem iogurte (ERRADO, pois comprei um OU outro).

c) não fui ao mercado. (ERRADO, se fiz compras, EU FUI ao supermercado)

d) só comprei creme (ERRADO, comprei creme E sabonete)

e) não comprei cereal nem pão (ERRADO, comprei cereal E pão)
Fazendo por eliminação, a questão fica até óbvia. De trás pra frente:

e) não comprei cereal nem pão. (ERRADO. Comprei pelo menos um dos dois)
d) só comprei creme. (ERRADO. Comprei creme e sabonete)
c) não fui ao mercado. (ERRADO. A expressão "Se não fui ao mercado, então não fiz compras" é equivalente a "Se fiz compras, então fui ao mercado". As afirmativas seguintes assumem que "fiz compras")
b) não comprei nem queijo nem iogurte. (ERRADO. Comprei exatamente um dos dois)
a) fui ao mercado e comprei sabonete. (CERTO. Pois, "se fiz compras, então fui ao mercado" e já sabemos que "fiz compras". Portanto, é verdade que "fui ao mercado". Também comprei sabonete, embora não somente)
p: fui ao mercado. q:fiz compras.

r:comprei creme. s. comprei sabonete.

t;comprei queijo. u:comprei iogurte.

v;comprei cereal. w:comprei pão.

(~p->q) ^ (r^s)^(t v u)^( V v W)

VL=VALOR LÓGICO

VL(~p ->~q)= V

~p->~q é equivalente ~~p v~q que é equivalente pv~q( fui ao mercado ou não fiz compras) se o valor de p for verdadeiro tanto faz o valor de ~q, pois a premissa já se torna verdadeira.

VL(r^s)= V, ou seja, a proposição r tem que ser verdadeira ea porposiição s também tem que ser verdadeira.

VL(t v u)= V, ou seja, aceitam os pares VV,VF,.FV (NÃO DÁ PARA DEDUZIR MUITA COISA.)

VL(V v W)= V, ou seja, aceitam os pares VV,VF,.FV (NÃO DÁ PARA DEDUZIR MUITA COISA.)

portanto, de concret que o podemos tirar e utilizar nas alternativas é p:fui ao mercado e r:comprei creme e s;comprei sabonete.
Eu raciocinei da seguinte forma:

Ele nos deu 4 premissas:

Se não fui ao mercado, então não fiz compras.
Comprei creme e sabonete.
Ou comprei queijo ou comprei iogurte.
Comprei cereal ou comprei pão.

Estipulei "comprei creme e sabonete" como verdadeira e fui direto às alternativas:

a) fui ao mercado e comprei sabonete. Correta! Se eu comprei creme e sabonete, então fui ao mercado e comprei sabonete.

b) não comprei nem queijo nem iogurte. Errada! Não posso afirmar que não comprei nem queijo e nem iogurte.

c) não fui ao mercado. Errada! Se comprei creme e sabonee, então fui ao mercado.

d) só comprei creme. Errada! Comprei creme e sabonete.

e) não comprei cereal nem pão. Errada! Mesma coisa da b. Não posso afirmar que não comprei cereal e nem pão.
Considerando as afirmativas verdadeiras, temos:

1) Começando com a conjunção:

Comprei creme e sabonete. ⇒ V ^ V = V

Logo, se comprei creme e sabonete são verdades, obrigatoriamente "não fui ao mercado" e "não fiz

compras" são falsos, assim:

2) Se não fui ao mercado, então não fiz compras. ⇒ F → F = V

As outras duas afirmações são disjunções, logo não temos como ter certeza sobre o valor lógico

das proposições simples que a compõe.

Assim, a única certeza que temos a partir da conjunção é que "fui ao mercado", "comprei

creme e sabonete" são verdades.

Letra A.

Vá e Vença!
Consegue-se responder a questão através do método tabela-verdade da relação conjunção pˆq (Comprei creme e sabonete), de onde deduz-se que ambas devem ser V. Em seguida parte-se para o método da equivalência da primeira afirmativa: condicional p-> q equivale a ˜q -> ˜p. Assim, afirma-se que: "Fiz compras" (V) e "Fui ao mercado" (V). Parafraseando o comentario de alguns colegas acima, a lógica argumentativa trata da FORMA e não do CONTEÚDO. Nao devemos pressupor que as compras e a ida ao supermercado são verdadeiras pelo simples fato de ter-se comprado sabonete e creme.
Respondi assim:
Com base no enunciado, tudo é verdade, se tudo é verdade, temos que ir a procura da premissa verdadeira.
Aí só dá para assumir como verdade, a conjunção. Então iniciei respondendo pela conjunção, a partir dela, só foi possível responder também o "se -> então" e vi que não daria para responder mais o resto e fui diretamente para as alternativas.

Nas alternativas, só havia uma resposta de acordo com o que foi possível responder, por que as demais não tinham sentido em relação a tabela, por que não havia caminho para seguir.

(F) ~mercado -> ~compras (F) = V

(V) comprei creme e comprei sabonete (V) = V
15. Considere verdadeiras as afirmativas:
P1) Se não fui ao mercado, então não fiz compras. Resumo: "não fui ao mercado" / "não fiz compras" / "fui ao mercado" / "fiz compras".

P2) Comprei creme e sabonete.Resumo: "comprei creme e sabonete" / "comprei creme" / "comprei sabonete". Obs. Só não posso afirmar que "só comprei creme" / "só comprei sabonete". Nas alternativas posso omitir um dos itens, mas não posso afirmar com a palavra "só".

P3) Ou comprei queijo ou comprei iogurte. Resumo: "comprei queijo e não comprei iogurte" / "comprei iogurte e não comprei queijo".

P4) Comprei cereal ou comprei pão. Resumo: "comprei cereal e não comprei pão" / "comprei pão e não comprei cereal

=====

A partir dessas afirmações, pode-se concluir que... Posso garantir que fui ao mercado, isso posso garantir !

(A) fui ao mercado e comprei sabonete. Correta. Não há necessidade de dizer que comprei creme.

(B) não comprei nem queijo nem iogurte. Errada.. ou comprei um ou comprei outro. "ou...ou" exige um ou outro.

(C) não fui ao mercado. Errada. As assertivas P2, P3 e P4 garantem que fui ao mercado.

(D) só comprei creme. Errada. Não posso afirmar isso, pois comprei creme e sabonete. Se não tivesse a palavra "só" estaria verdadeira também.

(E) não comprei cereal nem pão. Errada.. ou comprei um ou comprei outro.
ALTERNATIVA A (CORRETA)

EXPLICAÇÃO: "COMPREI CREME E SABONETE". Isso explica que ele comprei creme e sabonete no mercado. Então, como na alternativa A diz que comprou sabonete, essa é a alternativa correta.
EXPLICAÇÃO:
PASSO 1º: TRANSFORMAR AS PROPOSIÇÕES E SEUS RESPECTIVOS CONECTIVOS EM SIMBOLOGIA DE RACIOCÍNIO LÓGICO:
~p -> ~q
p ^ q
p v q
p v q
CONECTIVO (SE, ENTÃO) = “V” c “F” = “F”
CONECTIVO (E) = “V” c “V” = “V”
CONECTIVO (OU, OU) = “V” c “F” // “F” c “V” = V
CONECTIVO (OU) = AONDE TEM “V” = “V”

OBS: SOMENTE HOUVE ALTERAÇÃO NO CONECTIVO (SE, ENTÃO) TRANSFORMANDO O ~P EM P, TEM-SE QUE A NEGAÇÃO TORNA-SE UMA PROPOSIÇÃO VERDADEDIRA, OU SEJA: FUI AO MERCADO.
PASSO 2º: TRANSFORMAR AS PROSPOSIÇÕES E SEUS RESPECTIVOS CONECTIVOS EM FRASE ESCRITA NOVAMENTE, RETIRANDO-SE OS CONECTIVOS:

FUI AO MERCADO , NÃO FIZ COMPRAS
COMPREI CREME SABONETE
COMPREI QUEIJO COMPREI IOGURTE
COMPREI CEREAL COMPREI PÃO

LOGO: A ÚNICA RESPOSTA PRESENTE NO ESQUEMA ACIMA É A ALTERNATIVA A.
a resposta mais simples e facil é você transformar a frase negativa( que tem não antes do verbo) em positiva.
se fui ao mercado então fiz compras.
Gabarito A

Resolução da questão

https://youtu.be/6kH0ZRIJSUQ?t=15

fonte: FCC - 2014 - TRF 4ª REGIÃO - ESTRUTURAS LÓGICAS (www.gurudamatematica.com.br)
Quebrei cabeça à toa nessa hem...faltou atenção!
https://www.youtube.com/watch?v=6kH0ZRIJSUQ

Resolução da questão pelo professor Ivan Chagas.

ID

1242961

Banca

CESPE / CEBRASPE

Órgão

TRT - 17ª Região (ES)

Ano

2013

Provas

Disciplina

Raciocínio Lógico

Assuntos

Considerando a proposição P: “Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, aquele funcionário público será leniente com a fraude ou dela participará”, julgue o item seguinte relativo à lógica sentencial.

Se a proposição “Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude” for verdadeira, então a proposição P também será verdadeira.

Alternativas

Certo

Errado

Comentários

Considere:
A = Funcionário público que estiver sob pressão dos corruptores
B= funcionário público que estiver diante de uma oportunidade com baixo risco de ser punido,
C= funcionário público será leniente com a fraude
D= funcionário público dela (fraude) participará

A proposição P: “Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido,aquele funcionário público será leniente com a fraude ou dela participará”,ficará assim:
P = (A v B)--> (C v D)
A questão pede para ser analisada e julgada a seguinte proposição “Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude” for verdadeira, então a proposição P também será verdadeira.
Aqui está afirmando que:
B ^ D = V

A conjunção (e) só pode ser verdadeira se AMBAS as proposições forem verdadeiras, assim B= V e D = V,também.

Substituindo esses valores na equação de P, temos:
P = (A v B)--> (C v D)
P = (A v V) --> (C v V)

Mesmo não sabendo os valores de A e C, é fácil concluir que em ambas as disjunções (ou) o resultado é V, pois na disjunção basta apenas uma delas.
P = (A v V)--> (Cv V)
P = (V)--> (V)
P= V

Conclusão: a afirmação é verdadeira? CORRETO.
Tentando ser objetivo:
(Pressão V Oportunidade) -> (Leniente V Participará)
Enunciado Oportunidade (V) e Participará (V), substituindo temos:
(Pressão) -> (V)
Logo: Indiferente de Pressão ser (F) ou (V) dará (V)
A condição só é (F) em: (V) -> (F)
Fiz um vídeo com a resolução dessa questão, não deixem de ver.

Link para o vídeo com a resolução dessa questão: https://youtu.be/DCNowpGTVM8

Professor Ivan Chagas

Muito mais vídeos com questões resolvidas em www.facebook.com/gurudamatematica
Tabela verdade da condicional

Só sera falsa P->Q ( Quando P for Verdadeira e Q for Falsa )
Conclusão: Se Q tiver valor lógico verdadeiro, independente do valor de P a proposição será verdadeira.
A forma de composição de uma condicional : A-> B

A: antecedente

B: consequente

*No item da questão, há uma disjunção no consequente e outra no antecedente. ( A v B) -> ( C v D )

O enunciado manda colocarmos uma verdade na primeira disjunção e uma na segunda disjunção. E creio que nessa altura do campeonato, o senho(a) já sabe que sempre que tiver uma verdade na disjunção a proposição inteira será verdadeira, ficando assima representação gráfica :

A v B ( verdade ) -> C v D ( verdade ). Logo, verdadeira a proposição.

GABARITO "CERTO"
Explicando objetivamente:
p: Se estiver sobre pressão dos corruptores;
q: Diante de uma oportunidade com baixo risco de ser punido
r: Aquele func. público será leniente com a fraude
s: Dela participará
(PvQ) -> (RvS)
- - - - -
Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude” for verdadeira, então a proposição P também será verdadeira.
IÉ,
Q^S = verdadeiras (Q = V e S = V)
Logo está correta a assertiva, pois o consequente (Q^S) é verdadeiro, sendo que o antecedente poderá ser tanto V ou F que a condicional será sempre V
Certo
Considerando a proposição P: “Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, aquele funcionário público será leniente com a fraude ou dela participará”, julgue o item seguinte relativo à lógica sentencial.

A: SE estiver sob pressão dos corruptores
B: OU diante de uma oportunidade com baixo risco de ser punido
C: ENTÃO aquele funcionário público será leniente com a fraude
D: OU dela participará

(A v B) ---> (C v D)
V ----> V = V

No "ou" basta uma proposição ser verdadeira para ter valor verdadeiro.

Se a proposição “Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude” for verdadeira, então a proposição P também será verdadeira.

B ^ D = V
V ^ V = V

Gabarito CERTO
ERREI ESSA POR BOBAGEM
Perfeito Thiago Emanuel, questão fácil, mas tem que ter atenção.
CERTO

Estamos diante de uma preposição composta, CORRETO!!!

> “Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, aquele funcionário público será leniente com a fraude ou dela participará”

Na regra do se somente se, Sabemos que, a preposição será verdadeira quando ambas forem falsa ou verdadeiras. Logo, pecebemos que a preposição P e dada como verdadeira, se configurando como certa, quando se afirma na questão.

Lembre-se: O tempo de prova é curto, não dar, para fazer vários gráficos para se resolver questões, desta forma, você será prejudicado.

Bons Estudos.
Analisando a questão:

Reescrevendo a proposição P:

“Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, ENTÃO aquele funcionário público será leniente com a fraude ou dela participará"

Assim, organizando:

p = estiver sob pressão dos corruptores
q = diante de uma oportunidade com baixo risco de ser punido
r = aquele funcionário público será leniente com a fraude
s = dela participará

O que nos dá:

P: (p v q)→(r v s)

Se a proposição “Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude" for verdadeira, então é o mesmo que dizer:

q ^ s = V

Logo q e s obrigatoriamente precisam ser verdadeiros. Assim como P = (? v V)→(? v V), não nos importa mais os valores lógicos de ?, pois em uma disjunção, se uma das proposições for V, então automaticamente a mesma se torna V também.

Assim, pela tabela verdade da condicional (V)→(V) = V, ou seja a proposição P de fato será verdadeira se q e s forem V.

Resposta: CERTO.
Pra ser bem objetivo:

No '' V '' não pode ter FF, se a segunda parte da proposição P for verdadeira, independente da primeira parte, a proposição P será verdadeira.
https://www.youtube.com/watch?v=cvnTvnN-dcs&list=PL70rxKg7qWNUxCli2Pj1Y1Yurv2Xk4r0k&index=18

Indico essa video aula super top... É uma dica do Estratégia... vale a pena...
sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido ->> será leniente com a fraude ou

V/F V V/F

dela participará”

V

V/F v V = V

V --> V = V
P: “Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, aquele funcionário público será leniente com a fraude ou dela participará''.

“Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude” for verdadeira

Na frase temos uma condiconal-disjunção

A: Pressão dos corruptores

B: Diante de uma oportunidade V

C: leniente com a fraude

D: Participar da fraude V

A v B-> C v D

V/F v V-> V/F v V Na união(disjunção) será V se pelo menos uma das proposições for V

V ->V V

então a proposição P também será verdadeira. CERTO
“Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, [ENTÃO] aquele funcionário público será leniente com a fraude ou dela participará”

“Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido = VERDADEIRO

"Participará da fraude” = VERDADEIRO

(A v B) --> (C v D)

V ---> V

V

GAB: CORRETO
CERTO
PvQ ---> RvS

Q e S= verdadeiros,assim qualquer valor que colocar no ''R'' a proposição ( R v S) será VERDADEIRA. Pois, a única forma de ficar falso no Se, então é o Vera Fisher.
Minha contribuição.

P = (A v B) -> (C v D)
P = (A v V) -> (C v V)
P = V -> V = V
---------------------------------------------------------------------------------------------------------------------------------------------------------------

Tabela verdade da disjunção:

V v V = V
V v F = V
F v V = V
F v F = F

--------------------------------------------------------------------------------------------------------------------------------------------------------------

Tabela verdade da condicional:

V -> V = V
V -> F = F
F -> V = V
F -> F = V

Abraço!!!
“Se estiver sob pressão dos corruptores ou diante de uma oportunidade com baixo risco de ser punido, aquele funcionário público será leniente com a fraude ou dela participará”.

Se a proposição “Aquele funcionário público está diante de uma oportunidade com baixo risco de ser punido e participará da fraude” for verdadeira, então a proposição P também será verdadeira.

(A v VD) -> (VM v L) = V
É só marcar certo e correr para o abraço!!

ID

1248355

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2004

Provas

CESPE - 2004 - Polícia Federal - Agente da Polícia Federal - Regional

Disciplina

Raciocínio Lógico

Assuntos

Com base nas informações apresentadas no texto acima, julgue o item a seguir.

Se as proposições P e Q são ambas verdadeiras, então a proposição (¬ P) ∨ (¬ Q) também é verdadeira.

Alternativas

Certo

Errado

Comentários

(P ^ Q) são verdadeiras, então a proposição (¬ P) ∨ (¬ Q) negação.
V ^ V = V negando F v F= F
regra da disjunção inclusiva: falso quando dois falsos, verdadeiro nos demais casos.
Dica: evitem decorar regrinhas... isso gera confusão quando a ansiedade bate na hora da prova. Analisem apenas a veracidade da proposição, fazendo abstração das partes e depois analisando a proposição toda, é bem fácil.
Regrinha:

Transforme todos os valores da proposição em verdadeiro. Veja:
(¬P) v (¬Q)

(¬V) V (¬V)
F V F = F

Bons estudos!
(¬P) v (¬V)

F v F

=

F

Na disjunção inclusiva : Só será verdade se uma delas for Verdade
Errado.

(¬ P) ∨ (¬ Q) =
F V F = F

Disjunção inclusiva: F apenas quando for tudo F
Nestes tipos de questões , é essencial saber as regras dos conectivos. Nesta assertiva era necessário saber que na Disjunção(v) basta um verdadeiro para ser verdade.

Estudando e aprendendo com questões!

GAB ERRADO
vanderlei junior, eu tenho que te corrigir em algo.
A questão está errada mesmo, mas não é disjunção exclusiva, mas sim Disjunção, que é representado pelo símbolo V.

Vamos ter mais cuidado na hora de comentar, porque na tentativa de ajudar, pode acabar prejudicando as pessoas.
ERRADO

(¬ P) ∨ (¬ Q)

F V F =F
ERRADO

Trata-se de uma ''Conjunção'', que poderá ter valor Verdadeiro se ambas forem verdadeiras. Ex:

Comprei uma casa e um carro: Ambas Verdadeira

Não comprei a casa e nem o carro: Errado

Obs: A regra será que, somente em ambas verdadeira o resultado é verdadeiro caso contrário será falso.

Deus é Fiel!!!

“Treine enquanto eles dormem, estude enquanto eles se divertem, persista enquanto eles descansam, e então, viva o que eles sonham.”

(Provérbio Japonês)
p = V => ~p = F
q = V => ~q = F

(~p)v(~q) = (F)v(F) = F

GABARITO: ERRADO
Elas são equivalentes.
Se as proposições P e Q são ambas verdadeiras, logicamente ¬ P e ¬ Q são falsas, é o contrario certo?

(¬ P) ∨ (¬ Q) se não P é falsa e não Q é falsa , basta saber a regra do conectivo "OU" que diz: que sera verdadeira quando pelo menos uma for verdadeira, nesse caso as duas são falsas e por isso a questão esta errada.
ERRADO
Se as proposições P e Q são ambas verdadeiras, logicamente ¬ P e ¬ Q são falsas, é o contrario certo?

(¬ P) ∨ (¬ Q) se não P é falsa e não Q é falsa , basta saber a regra do conectivo "OU" que diz: que sera verdadeira quando pelo menos uma for verdadeira, nesse caso as duas são falsas e por isso a questão esta errada.
ERRADO
Se as proposições P e Q são ambas verdadeiras, logicamente ¬ P e ¬ Q são falsas, é o contrario certo?

(¬ P) ∨ (¬ Q) se não P é falsa e não Q é falsa , basta saber a regra do conectivo "OU" que diz: que sera verdadeira quando pelo menos uma for verdadeira, nesse caso as duas são falsas, então o resultado vai ser falso, e por isso a questão esta errada.
ERRADA
se P e Q são verdadeiras então , ~P e ~Q serão falsas.
da disjunção F com F da F e não V como afirma a questão.
Se a questão falou que P E Q são VERDADEIROS
E a proposição apresentada esta NEGANDO essas proposições
Então elas apresentam valor lógico falso
(~ P) F V (~Q) F
Na tabela verdade do conectivo v
Para ser verdade basta que a tabela me de uma Verdade
Como todas as minhas proposições deram Falsas ou seja nenhuma verdade ,consequentemente a proposição inteira sera FALSA

F v F = F

Também estou aprendendo RLM Espero ter contribuído
qualquer erro favor me notificar
A questão afirma que ambas são Verdadeiras,e a mesma as nega depois.Portanto,se P ^ Q são verdadeiras, a proposição negação (~P)v(~Q) não pode ser verdadeira.
F v F=F
❌Gabarito Errado.
A questão diz que ambas são verdadeiras, sendo que ambas possuem negação, logo tudo fica falso. E quando tudo está falso em uma Disjunção é falso e não verdadeiro como afirma a questão.
(¬P) v (¬V)
F v F
F.
https://youtu.be/Dt3Lg5ECWIk
1min 30 seg
P e Q
v e v = VERDADEIRO

Obs: O conectivo "e" "^" é muto Exigente só aceita se as duas proposições forem verdadeiras.

~P ou ~Q
F ou F = FALSO

Obs: O conectivo "ou" "v" só é falso em uma condição quando as duas proposições forem falsas.
P ∨ Q são verdadeiras e seu OPOSTO é (¬ P) ∨ (¬ Q) que fica = F ou F = F
Conclusão: falso com falso no conectivo ''OU'', é falso. Portanto, a questão está errada ao afirmar que (¬ P) ∨ (¬ Q) também é verdadeira.
Na hora pensei até em fazer a tabela verdade rsrsr, mas nem precisou. GAB: Errado.

F v F = Falso
Errado!
Na disjunção inclusiva a proposição só será falsa se todas as proposições forem falsas.
Tabela verdade da inclusiva (ou l v):
VVV
VFV
FVV
FFF
Logo, se as duas são falsas (¬ P) ∨ (¬ Q), então a proposição é falsa.

ID

1248358

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2004

Provas

CESPE - 2004 - Polícia Federal - Agente da Polícia Federal - Regional

Disciplina

Raciocínio Lógico

Assuntos

Com base nas informações apresentadas no texto acima, julgue o item a seguir.

Se a proposição T é verdadeira e a proposição R é falsa, então a proposição R ➔(¬ T) é falsa.

Alternativas

Certo

Errado

Comentários

Na condicional só é falsa quando a primeira é verdadeira e a segunda falsa. T é verdadeira, logo nãoT é falsa portanto questão errada.
Na condicional = Só da FALSO se for de V para F
Na condicional = Vera --> Fischer = Falsa, o resto é tudo verdadeiro.
a velha e boa vera fisher...
Simples, T = v, R= f, Depois ele fala que negou T, agora T = f, no condicional o resultado de F+F= V, e não falso como diz a pergunta.. Questão errada..
Errado.

R ➔(¬ T) =
F ➔ F = V
ERRADO

BASTA PERCEBER QUE A PRIMEIRA PARTE TEM VALOR LÓGICO FALSO

LOGO,NÃO TEM COMO A PROPOSIÇÃO DAR FALSA.
T = V => ~T = F
R = F

R -> (~T) = F -> (F) = V

GABARITO: ERRADO
NO (SE.. ENTÃO) COMEÇANDO COM F SEMPRE SERÁ VERDADEIRO.
Que delícia de questão!

R ➔(¬ T) =
F ➔ F = V

Gaba: errado.
Se a proposição T é verdadeira e a proposição R é falsa, então a proposição R ➔(¬ T) é falsa.

A assertiva diz que R é falsa, e o apresenta aqui R ➔(¬ T) em primeiro.
Ora, começou com falso, nem precisa ver o resto, R ➔(¬ T) é verdadeiro!

Gabarito ERRADO.
T é V E R é F V e F= F
F se, então F= V
Questão é falsa? Não é Verdadeira
Gabarito Errado
ERRADA
"R" É FALSO MAS O "NÃO T" SE TORNA FALSA : FF : VERDADEIRA NA CONDICIONAL
NEM PRECISA SABER O VALOR LOGICO DE T NESTA QUESTÃO PRA SABER QUE É VERDADEIRA
SO VERA FICHER PRA DAR FALSO.
ERRADA Nesse caso só se altera o valor de lógico de ~T que será "F". E como a regra tem de ser "Vera Fischer é falsa", já nesse caso o valor lógico de R=F e ~T=F no caso resulta numa proposição "V."
Errado.

R --> (~T)

F --> ~V

F--> F = V
Errado!
Na condicional a proposição só será falsa se a primeira for verdadeira e a segunda for falsa.
Tabela verdade da condicional (se... então l ➔):
VVV
VFF
FVV
FFV
Logo, só por R ser falsa já conseguimos concluir que a proposição é verdadeira, independente de T ser verdadeira ou falsa.

ID

1248361

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2004

Provas

CESPE - 2004 - Polícia Federal - Agente da Polícia Federal - Regional

Disciplina

Raciocínio Lógico

Assuntos

Com base nas informações apresentadas no texto acima, julgue o item a seguir.

Se as proposições P e Q são verdadeiras e a proposição R é falsa, então a proposição (P ∧ R) ➔(¬ Q) é verdadeira.

Alternativas

Certo

Errado

Comentários

Como resolvi!(P ∧ R) ➔(¬ Q)
Primeiro PASSO : (P ∧ R)
P ∧ R -> para ∧ só vai ser verdadeira quando ambas forem verdadeira
V F F
F V F
Segundo PASSO (➔) Para este só vai ser falso quando a primeira for verdadeira e a segunda for falsa.
Terceiro PASSO então já temos um (F) do primeiro passo e (➔) do segundo e um (¬ Q) que é negado
logo temos F➔F resultado verdadeiro pois ➔ só vai ser falso quando a primeira for falsa e a segunda verdadeira.
Questão CERTAAA!!
Se a primeira parte da Condicional for falsa, o resultado será sempre verdadeiro...
resolvi a sim.
( P ∧ R ) ➔ ( ¬ Q )
( V ∧ F ) ➔ (~ V ) = é verdadeira.
F ➔ F = V
Certo.

Resolvi da mesma forma que Lucas Rocha, que, na minha opinião, é o modo mais prático e rápido p resolver esse tipo de questão
(tempo de prova eh importante neh....)
Eu acertei, mas fiquei meio encucado com a resposta que vi dessa questão em um video de Abel Mangabeira, onde ele resolve essa questão e diz que ta errada.

mas assim como a banca colocou certa os colegas aqui que já responderam colocaram certas também, bom eu marquei como certa.
Esse tipo de questão te exige domínio da técnica, porém o problema de fato é o pega ratão, tem que estar concentrado para fazer a correta interpretação do jogo que a banca propõe ali.

A questão está bem elaborada, não tem nenhum erro.
FRANCISCO RAMOS

Eu tbm Mais ele errou certeza cara nao tem como isso ta errado so da falsa quando vai a festa quando nao e tudo verdadeira
P             Q            R             T             P^R        (P^R)→(~R)

V             V             V             V             V F

V             V             F             V             F V

V             V             V             F             V F

V             V             F             F             F V
p = V
q = V => ~q = F
r = F

(p^r) -> (~q) = (V^F) -> (F) = (F) -> (F) = V

GABARITO: CERTO
(P^R) -> (~Q)

(V^F) - > (~V)

F -> F

V
a primeira substitui de acordo com que a questão sugeriu

( V ∧ F ) ➔ ( ¬ V )

( V ∧ F ) ➔ ( F )
       F     ➔   F    = (V) . . SE..ENTÃO, só vai ser falso quando for ( FV), então é VERDADEIRA

Segunda substitui tudo por (F )

( F ∧ F ) ➔ ( ¬ F )

( F ∧ F ) ➔ ( V )
       F     ➔   V   = (V) . SE..ENTÃO, só vai ser falso quando for ( FV), então é VERDADEIRA
Quando o antecendente for falso, a proposição será verdadeira independente do valor do consequente!
Questão fácil! Há se todas fossem assim!
Só complementando o comentário do Danilo

NA CONDICIONAL, Quando o antecedente for falso, a proposição será verdadeira independente do valor do consequente!

#PERTENCEREMOS
INSTA: @_CONCURSEIROPRF
Que prova boa de RLM essa de 2004 na PF!!
( V ∧ F ) ➔ ( ¬ V )
( V ∧ F ) ➔ ( F )
F ➔ F = (V)
Se as proposições P e Q são verdadeiras e a proposição R é falsa, então a proposição (P ∧ R) ➔(¬ Q) é verdadeira.

Vamos por parte:

(P ∧ R) é falso pois a questão diz que R é falso e P é verdadeiro, sendo essa uma CONJUNÇÃO, se um dos dois for falso, a sentença é falsa!

(P ∧ R) ➔(¬ Q) sendo falso a primeira parte da CONDICIONAL, ela é SEMPRE verdadeira.

(não precisa perder tempo com o restante)

Gabarito CERTO.
só é FALSA se for VERA FISCHER FALSA

Jhoni zini
✅Gabarito Certo.
V + condicional+ F = F se não for nessa ordem é verdadeiro.
(P ∧ R) ➔(¬ Q)
(V ∧ F )➔(¬ V)
F ➔ F
V
Segue a regra que é sucesso.
Bons estudos!✌
~V?
V ^ F -> F
F -> F = V
Essa metodologia está errada?
GAB. CERTO

( V ∧ F ) ➔ (~ V ) = é verdadeira.
F ➔ F = V

ID

1248373

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2004

Provas

CESPE - 2004 - Polícia Federal - Agente da Polícia Federal - Regional

Disciplina

Raciocínio Lógico

Assuntos

Considere que as letras P, Q, R e T representem proposições e que os símbolos ¬, ∧, ∨ e ➔ sejam operadores lógicos que constroem novas proposições e significam não, e, ou e então, respectivamente. Na lógica proposicional, cada proposição assume um único valor (valor-verdade), que pode ser verdadeiro (V) ou falso (F), mas nunca ambos.

Considere as sentenças abaixo.

I Fumar deve ser proibido, mas muitos europeus fumam.
II Fumar não deve ser proibido e fumar faz bem à saúde.
III Se fumar não faz bem à saúde, deve ser proibido.
IV Se fumar não faz bem à saúde e não é verdade que muitos europeus fumam, então fumar deve ser proibido.
V Tanto é falso que fumar não faz bem à saúde como é falso que fumar deve ser proibido; conseqüentemente, muitos europeus fumam.

Considere também que P, Q, R e T representem as sentenças listadas na tabela a seguir.

            P Fumar deve ser proibido.
            Q Fumar de ser encorajado.
            R Fumar não faz bem à saúde.
            T Muitos europeus fumam.

Com base nas informações acima e considerando a notação introduzida no texto, julgue o item seguinte.

A sentença IV pode ser corretamente representada por (R ∧ (¬ T)) ➔ P.

Alternativas

Certo

Errado

Comentários

Errado

A sentença I deve ser corretamente representada por P ∧ T.
Certo

Fácil é só unir as sentenças, muito fácil.
Não concordo com ivone, a questão na verdade tenta confundir o candidato tentando passar uma suposta equivalencia da condicional; se...então. ( -> )
o "mas" é sinônimo da conjunção, então se você conhecer o sinônimo, não tem como se confundir. P ^ T
Muito simples, a negação da conjunção é a disjunção. Por isso a questão está errada.
P fumar deve ser proibido II Fumar não deve ser proibido ~P ^(e)
R Fumar não faz bem à saúde II fumar faz bem à saúde. ~R (negação dupla no não)
Logo,( ~P) ^ (~R)
Mas eu tinha errado a questão...hehehee
Não entendi.
No meu entender a negação de P deveria ser: "NÃO fumar deve ser proibido". Negação no primeiro verbo.
O Cespe já fez isso antes ...
Fácil só completar as sentenças e pronto.
F ^ F = F
II - Fumar não deve ser proibido e fumar faz bem à saúde.
P: Fumar deve ser proibido = V (~P) ^ (~R) =
R: Fumar não faz bem à saúde = V F ^ V = F
sentença I) Fumar deve ser proibido, mas muitos europeus fumam.

P = Fumar deve ser proibido.

T = Muitos europeus fumam.

¬ T = Muitos europeus NÃO fumam.

Para a questão ser VERDADEIRA, a sentença I DEVE ser corretamente representada por P ∧ ( T) e NÃO por P ∧ (¬ T).
concordo com o luizmedina
R^¬ T➔ P.... arrumando:( R^(¬ T))➔ P
eu também acho que está errado.
Então, meus colegas, consegui resolver depois de muitas horas, vejam:

1º Passo: Quando o problema diz para considerar P, Q, R e T, deve ser utilizada a regra dada.
2º Passo: Então, direciono na sentença IV e transformo a frase em símbolos utilizando as letras dadas do 1º passo.
3º Passo:Logo,
Sentença: (Se fumar não faz bem à saúde) e (não é verdade que muitos europeus fumam), então fumar deve ser proibido.
Regras dada: R Fumar não faz bem à saúde. T Muitos europeus fumam. P Fumar deve ser proibido.
(R ∧ (¬ T)) ➔ P.
Procurei em sites e achei algumas respostar C e outras E. Eu não entendi está questão.
Temos a proposição IV que nos diz:

"Se fumar não faz bem à saúde E não é verdade que muitos europeus fumam, então fumar deve ser proibido."

É sabido que a proposição acima é uma condicional e que P = Fumar deve ser proibido, Q = Fumar de ser encorajado, R = Fumar não faz bem à saúde e T = Muitos europeus fumam. Assim, reescrevendo:

(R ^ ~T)→P
Resposta: Certo.
Certo.

A questão descreveu corretamente a quarta opção do enunciado...
PS: o "¬" nega o valor lógico....tem que ter cuidado....
Esses comentários as vezes atrapalham kkk a questão está certa como a Jemima e a Bruna disseram.
A questão não quer saber os valores V ou F das preposições, ela quer a sentença que corresponde a IV.

Questão CERTA
P Fumar deve ser proibido.
            Q Fumar de ser encorajado.
            R Fumar não faz bem à saúde.
            T Muitos europeus fumam.

Segue abaixo as representação lógica das proposições
I: P ^T
II: ~P ^ ~R
III: R => P
IV: ( R ^ ~T ) => P
V: (~R ^ ~P) => T

Lembrando alguns sinônimos de conectores lógicos :
^ = e = mas; nem; tanto...... como....; também; virgula.
=> = se.... então = quando....; como; caso; logo; consequentemente; condicionado; pois; porque; "ideia de condição".
Vejo algumas pessoas dizendo que é fácil .Hoje concordo com quem diz , entretanto quem fala isso so não informa que para eu chegar no nível de achar uma questão desta fácil , foram necessários 3 anos de estudo , 12 provas , 9 reprovações , e centenas de horas de estudos com planejamento de revisão de 48 horas , 7 dias , 15 dias e 30 dias , mais um simulado por semana depois da publicação do edital .Não menospreze quem esta estudando dizendo que é fácil .Mostre as pessoas o caminho para se tornar fácil .
Questão toda errada . tem gente justificando ainda meu Deus..
Ao meu ver, questão flagrantemente errada!
Vou dar a receita do sucesso:
Reclame menos das questões e se esforce mais para entender o que a banca entende como certo, afinal ficar reclamando não vai te levar a lugar algum.
Sejam objetivos no final da explicação,queremos saber se a questão esta CERTO ou ERRADO, já que os 'ainda' pobres só tem direito a 10 questões por dia kk
os comentários são de 6 anos atrás,será que vocês já conseguiram o concurso desejado e hoje exercem a profissão? eu espero que sim
QUESTÃO ERRADÍSSIMA
Uma duvida.

A representação de: Não é verdade que muitos europeus fumam = ~(T)

Não seria isso ?
Errado não + e + não = nem
Para quem tem dificuldade nesse tipo de questão: Professor Guilherme Neves.

Fui alfabetizado em lógica graças a ele.
✅Gabarito Correto.
Para resolver essa questão o primeiro passo que deve ser feito é identificar os conectivos lógicos presente na sentença IV.
Para depois comparar com está sentença : (R ∧ (¬ T)) ➔ P.
⚫Primeiro Passo: descobrir os conectivos.
IV (Se)fumar não faz bem à saúde(e)não é verdade que muitos europeus fumam, (então) fumar deve ser proibido.
Se fumar não faz bem à saúde ^ não é verdade que muitos europeus fumam, ➔ fumar deve ser proibido.
⚫Segundo Passo: Seguir o que a questão pede do P, Q, R, T.
Fumar não faz bem à saúde = R / não é verdade que muitos europeus fumam = ~T / Fumar deve ser proibido. = ➔ P.
⚫Terceiro Passo: Comparar com o que escrevi no segundo passo.
(R ∧ (¬ T)) ➔ P.
Veja que tem uma negação e antes da negação do T tem o conectivo E, logo a negação pode ser isolada por parênteses, para ser resolvido primeiro.
Dica: Não saía da questão até você ter entendido completamente, tente resolver o problema essa é a solução.
Bons estudos.
Onde está a sentença, QC? Para mim não aparece absolutamente nada.
IV) Se fumar não faz bem à saúde e não é verdade que muitos europeus fumam, então fumar deve ser proibido.
R ∧ ¬ T ➔ P

P: Fumar deve ser proibido.
Q: Fumar de ser encorajado.
R: Fumar não faz bem à saúde.
T: Muitos europeus fumam.

ID

1248376

Banca

CESPE / CEBRASPE

Órgão

Polícia Federal

Ano

2004

Provas

CESPE - 2004 - Polícia Federal - Agente da Polícia Federal - Regional

Disciplina

Raciocínio Lógico

Assuntos

Com base nas informações acima e considerando a notação introduzida no texto, julgue o item seguinte.

A sentença V pode ser corretamente representada por T ➔ ((¬ R) ∧ (¬ P)).

Alternativas

Certo

Errado

Comentários

Essa me pegou por falta de atenção:
Resumindo tudoooo.... v -> F ; Jamais será; F -> V
Ponto e fecho lá.
As sentenças são corretamente apresentadas da seguinte forma:
Sentença 1: P∧T
Sentença 2: ~P∧~R
Sentença 3: R --> P
Sentença 4: (R∧~T) --> P
Sentença 5: (~R∧~P) --> T

Bons Estudos.
Deveria ser ((¬ R) ∧ (¬ P)) ➔ T , pois é necessário verificar quem é a condição suficiente e a condição necessária
Mas gente, em nenhuma momento da questão fala qual é o valor de alguma proposição. Como poderemos calcular se não sabemos pelo menos um valor lógico. As sentenças listados podem ser tanto f como v, sejam as simples ou as compostas, caso em que na questão não afirma nenhuma
É sabido que p→p não é o mesmo que p→q. Assim T → ((~R) ∧ (~P)) pode ser reescrita como:

Se muitos europeus fumam, então é falso que fumar não faz bem à saúde e é falso que fumar deve ser proibido.

Percebam que a sentença V inverte a ordem da condicional acima, logo a forma correta de representar a sentença V é:

((~R) ∧ (~P)) → T
Resposta: Errado.
Caro Rafael, a presente questão não exige encontrarmos os valores lógicos, mas sim a montagem das sentenças usando as letras que representam as proposições, juntamente com os quantificadores lógicos.
T ➔ ((¬ R) ∧ (¬ P)) = Se muitos europeus fumam, então fumar não faz bem à saúde e fumar não deve ser proibido.
Fiz desse jeito..
T ➔ (¬ R) ∧ (¬ P) NÃO É A MESMA COISA QUE (¬ R) ∧ (¬ P) ➔ T

GABARITO ERRADO
Errado.

O T ➔ deveria vir na ordem como está a sentença....o erro está na antecipação de tal valor lógico
Pensei no consequentemente como uma condicional invertida, assim como o pois.
To esperando uma dessas dia 15. Pode ter certeza !!!!!
Não foi dificil. Talvez a pessoa se enrolaria na leitura e na intepretação. Mas em si, foi suave. Nada além do que a gente nunca viu, só foi cobrado de uma forma pouco vista.
Por ser uma proposição condicional, não pode haver a comutação entre os elementos, ou seja , não posso inverter a ordem, tenho que partir do antecedente (condição suficiente) para o consequente, neste caso: Tanto é falso que fumar não faz bem à saúde (¬ R) como (∧) é falso que fumar deve ser proibido (¬ P) ; conseqüentemente, muitos europeus fumam (➔T) , ficando: ((¬ R) ∧ (¬ P)) ANTECEDENTE ➔T CONSEQUENTE.
Questão errada.
O correto = ((¬ R) ∧ (¬ P)) ➔ T
Tanto... como da ídeia de (∧).
Questão maldosa!

T ➔ ((¬ R) ∧ (¬ P)) é o mesmo que: Se muitos europeus fumam, então fumar faz bem à saúde e não deve ser proibido.

A frase dada está em ordem diferente:"Tanto é falso que fumar não faz bem à saúde como é falso que fumar deve ser proibido; conseqüentemente, muitos europeus fumam", sendo representada por (¬ R) ∧ (¬ P) ➔ T

A questão alterou a ordem das proposições. Consequentemente sua forma de representação também foi alterada.
            P Fumar deve ser proibido.
            Q Fumar de ser encorajado.
            R Fumar não faz bem à saúde.
            T Muitos europeus fumam.

Segue abaixo as representação lógica das proposições

I: P ^T
II: ~P ^ ~R
III: R => P
IV: ( R ^ ~T ) => P
V: (~R ^ ~P) => T

Lembrando alguns sinônimos de conectores lógicos :

^ = e = mas; nem; tanto...... como....; também; virgula.

=> = se.... então = quando....; como; caso; logo; consequentemente; condicionado; pois; porque; "ideia de condição".
P-->Q NÃO É EQUIVALENTE A Q-->P
Equivalência do "se então"
P-->Q = ~Q-->~P (Modus tolens)
P-->Q = P suficiente para Q
P-->Q = Q necessário para P
P-->Q = ~P v Q (NEyMA, NEga a primeira ou MAntém a segunda)
"Consequentemente" é sinônimo de condicional, mas mantém sua estrutura igual.

Se estudo, então passo

=

Estudo consequentemente passo
CREIO QUE A ALTERNATIVA SEJA FALSA PELA SEGUINTE AFIRMAÇÃO:

ELA É UM PARADOXO E ESTE SENDO ASSIM NÃO É PROPOSIÇÃO!!

VEJAMOS: V - Tanto é falso que fumar não faz bem à saúde como é falso que fumar deve ser proibido.......

PORQUE ELA TRÁS A SEGUINTE IDEIA QUE É UMA MENTIRA AQUILO QUE ELA PROPÕE E ESSA IDEIA É UM PARADOXO QUE, REPITO, NÃO É CONSIDERADA PROPOSIÇÃO!!
Se muitos europeus fumam, então é falso que fumar não faz bem à saúde e é falso que fumar deve ser proibido.

Percebam que a sentença V inverte a ordem da condicional acima, logo a forma correta de representar a sentença V é:

((~R) ∧ (~P)) → T
Essa eu deixaria em branco! kkk
Em outras palavras a questão queria saber se a representação era equivalente a proposição
Logo, está errado, pois as equivalências do condicional são:
Ne y mar= nega ou mantém;
Inverte e nega tudo.

E na questão só inverteu, teria que negar tudo!
Deveria ser ((¬ R) ∧ (¬ P)) ➔ T

A CONDICIONAL NÃO ACEITA A COMUTATIVIDADE. ALIÁS, É A ÚNICA CONJUNÇÃO QUE NÃO ACEITA.
Como cheguei no resultado: só é f se der v f : f ----> v : v / e f

v e f : f

e : para ser verdadeira temos que ter dois vv : logo é f
A condicional é a única proposição que não tem propriedade comutativa !!!!!!!!
A condicional é a única proposição que não tem propriedade comutativa !!!!!!!!
A condicional é a única proposição que não tem propriedade comutativa !!!!!!!!
Tá, mas o que caralhos significa a propriedade comutativa??
Se trocar a ordem mantém o sentido.
Como a CONDICIONAL NÃO tem essa propriedade
Se trocou a ordem, mudou todo o sentido.

Ex: Se estudo, então trabalho.
                 É diferente de
        Se trabalho, então estudo

No caso:
T ➔ (¬ R) ∧ (¬ P)

DIFERENTE DE

(¬ R) ∧ (¬ P) ➔ T

Continue Firme na Luta!!!!!
#Dattebayo
Dica: Responda sem olhar assertiva e vá por partes!!

  P Fumar deve ser proibido.
  R Fumar não faz bem à saúde.
  T Muitos europeus fumam.

A princípio vc tem isso: Tanto é falso que fumar não faz bem à saúde como é falso que fumar deve ser proibido;

~R e ~P

e depois: conseqüentemente, muitos europeus fumam...

Muita atenção, pois aqui está apontando o RESULTADO! A CONSEQUÊNCIA da ação anteriormente citada, assim representado:

➔T

LOGO: (~R ∧ ~P) ➔ T

(Reparem que a banca tentou confundir colocando a CONSEQUÊNCIA no lugar da CAUSA!!!! T ➔ ((¬ R) ∧ (¬ P)) CUIDADO ISSO ESTÁ ERRADO!!!)

Na CONDICIONAL essa inversão muda o sentido da proposição. Na condicional, a ordem dos tratores altera o viaduto :D

Gabarito ERRADO.
Droga eu sei fazer a questão mas viagem na maionese kkk
errei porque pensei no CONDICIONAL INVERTIDO (POIS) .... =[
qnd nao vi o "muitos europeus fumam" no começo da frase ja concluí como falsa! esse meu pensamento foi certo ou dei sorte?
Condicional não permite comutativa, diferente do OU
Gabarito: errado.
É necessário seguir as seguintes etapas:
• 1ª etapa: analisando a Sentença V:
• sentença V = “tanto é falso que fumar não faz bem à saúde como é falso que
fumar deve ser proibido; consequentemente, muitos europeus fumam” = “se
é falso que fumar não faz bem à saúde e é falso que fumar deve ser proibido;
consequentemente, muitos europeus fumam”;
• ¬R = é falso que fumar não faz bem à saúde;
• ∧ = “e” = “como”;
• ¬P = é falso que fumar deve ser proibido;
• → = “se, então” = Tanto, consequentemente”;
• T = Muitos europeus fumam;
• sentença V = [(¬R) ∧ (¬P) → T].
• 2ª etapa: análise final:
Portanto, a sentença V pode ser corretamente representada por [(¬R) ∧ (¬P) → T].
Note que a proposição: [(¬R) ∧ (¬P) → T] é diferente da proposição: T → ((¬R) ∧
(¬P)). Diante disso, o item encontra-se errado

ID

1256860

Banca

CESPE / CEBRASPE

Órgão

INPI

Ano

2013

Provas

CESPE - 2013 - INPI - Tecnologista em Propriedade Industrial

Disciplina

Raciocínio Lógico

Assuntos

No conjunto de todas as frases, as proposições encontram-se entre aquelas classificadas como declarativas e verbais, ou seja, entende-se como proposição todo conjunto de palavras ou símbolos que exprimam um pensamento de sentido completo, para o qual seja possível atribuir, como valor lógico, ou a verdade ou a falsidade. Assim, as proposições transmitem pensamentos, isto é, afirmam fatos ou exprimem juízos que se formam a respeito de determinados entes. Com base nessas informações, julgue se o item a seguir é proposição.

Que excelente local de trabalho!

Alternativas

Certo

Errado

Comentários

Errado.
Classificação de uma proposição
Uma proposição pode ser classificada como sentença aberta quando não se pode atribuir um valor lógico verdadeiro ou falso para ela (ou valorar a proposição!), portanto, não é considerada frase lógica ou sentença fechada; quando a proposição admitir um único valor lógico, seja ele verdadeiro ou falso, nesse caso, será considerada uma frase, proposição ou sentença lógica.
Por exemplo, são consideradas sentenças abertas:
I. As frases interrogativas:
a) Quando será a prova?
b) Estudou o suficiente?
c) Ontem choveu?
II. As frases exclamativas:
a) Passei!
b) Gol!!!
c) Que lindo!
III. As frases imperativas:
a) Estude e leia com atenção.
b) Desligue seu celular.
c) Visite sua avó nesse domingo.
IV. As frases sem sentido lógico (expressões vagas, paradoxais, ambíguas, ...):
a) Proibido estacionar.
b) Acho que vai chover.
c) “esta frase é verdadeira”. (expressão paradoxal)
d) Ninguém é de ninguém.
e) Ele é o melhor amigo que tenho. (expressão vaga)
f) 2 + 5 + 7 + 4.
g) O cachorro do meu vizinho morreu. (expressão ambígua)
As sentenças exclamativas não são proposições porque não podem ser julgadas nem como verdadeiras nem como falsas.
Não se trata de uma proposição porque não é possível julgar a exclamação, assim como nos casos de sentenças interrogativas, sem verbo, verbos no imperativo e sentenças abertas.
Que excelente mamata!
Errada.
Frase exclamativa não é proposição.
Gabarito: E

As sentenças interrogativas, imperativas e exclamativas não são proposições porque não podem ser julgadas nem como verdadeiras nem como falsas. Exemplos: (i) a frase interrogativa "Pelé marcou mais de mil gols?'' não é uma proposição; (ii) a frase exclamativa "Pelé marcou mais de mil gols!'' também não é uma proposição; (iii) a frase imperativa "Pelé, marque mais de mil gols'' também não deve ser considerada como uma proposição.

Fonte: http://logicadescomplicada.blogspot.com.br/2010/07/que-e-proposicao.

Se quiser aceitar, lá vai um humilde conselho: não subestime questões como essa. Pode parecer muito fácil e justamente por isso a gente não observa bem e acaba, muitas vezes, escorregando nas cascas de banana deixadas pela banca.
Vem ni mim!
Eu acho que nunca mais a banca coloca uma dessa!!!
Nem todas as frases são proposições. A saber:

- Sentenças interrogativas;
- Exclamativas; ( Exemplo da questão )
- Imperativas;
- Sem valor lógico;
- Sem verbo.

--

Gabarito: Errado
Frases no IMPERATIVO, ou seja, exprimindo uma ordem, NÃO são proposições. A mesma coisa acontece em frases EXCLAMATIVAS, INTERROGATIVAS, SEM VERBO E SENTENÇA ABERTA.
Errado.
Errado – Frase exclamativa.

Questão comentada pelo Prof. Márcio Flávio
ERRADO
Não são proposições lógicas:
Frases exclamativas: “Meu Deus!”
Frases interrogativas: “Você me ama?”
Frases imperativas: “Não estude para passar, mas até passar!”
Frases sem verbo: “O mundo dos concursos públicos.”
Frases abertas: “x + 1 = 7” ; “Ela é a melhor esposa do mundo.”
Frases paradoxais: “Só sei que nada sei.”
Minha contribuição.
Proposição: Pode ser julgada como verdadeira ou falsa.
-Neymar é um péssimo jogador. (proposição)
-Ele é um ótimo desenhista. (não é proposição / sentença aberta)
-Traga o exercício amanhã. (não é proposição / frase imperativa)
-Existe vida após a morte. (proposição)
-Bom dia! (não é proposição / frase exclamativa)
-X + 1 = 4 (não é proposição / sentença aberta)
-2 + 1 = 0 (proposição)
-Qual o seu nome? (não é proposição / frase interrogativa)
Abraço!!!
NÃO SÃO PREPOSIÇÕES:
- SENTENÇAS EXCLAMATIVAS
- SENTENÇAS INTERROGATIVAS
- SENTENÇAS IMPERATIVAS/ORDENS
- PARADOXOS" ESSA FRASE É UMA MENTIRA"
- SENTENÇAS ABERTAS "PRONOMES ELE(A) AQUELE(A)/ X,Y ..."

ID

1256863

Banca

CESPE / CEBRASPE

Órgão

INPI

Ano

2013

Provas

CESPE - 2013 - INPI - Tecnologista em Propriedade Industrial

Disciplina

Raciocínio Lógico

Assuntos

Alternativas

Certo

Errado

Comentários

Aparentemente poderia ser um paradoxo, mas a frase é facilmente reconhecida como verdadeira pela teoria dos conjuntos. Há o conjunto dos políticos que contém dois subconjuntos: desonestos e não desonestos. Marcos não pertence ao conjunto dos políticos e portanto não poderá pertencer a nenhum dos dois subconjuntos.
gab C - É possível valorar tal proposição composta pela teoria dos conjuntos, uma vez que, se Marcos não é um político(verdade), então Marcos não é um político desonesto(verdade).
Certa
Esse "pois" está com sentido de "Se...Então..."
Antecedente: "não é um político."
Consequente: "Marcos não é um político desonesto."

"Se Marcos não é um político, então ele não é desonesto"
kkkkkkkkkkkkkkkkkk é necessário não ser político para ser honesto. Logo, é suficiente não ser desonesto para não ser considerado político. Chocante!
É uma proposição condicional.
Nem todas as frases são proposições. A saber:

- Sentenças interrogativas;
- Exclamativas;
- Imperativas;
- Sem valor lógico;
- Sem verbo.

Macete:

SEXI SEM LÓVER

--

É estranho, mas acostuma hehe
Variações da condicional (P -->Q): quando; pois; como; sempre que; toda vez que; desde que.
Certo.
Certo – Frase de sentido completo (o “pois” dá a ideia de “Se... então...”).

Questão comentada pelo Prof. Márcio Flávio
CERTO
Minha contribuição.
Proposição: Pode ser julgada como verdadeira ou falsa.
-Neymar é um péssimo jogador. (proposição)
-Ele é um ótimo desenhista. (não é proposição / sentença aberta)
-Traga o exercício amanhã. (não é proposição / frase imperativa)
-Existe vida após a morte. (proposição)
-Bom dia! (não é proposição / frase exclamativa)
-X + 1 = 4 (não é proposição / sentença aberta)
-2 + 1 = 0 (proposição)
-Qual o seu nome? (não é proposição / frase interrogativa)
Abraço!!!

ID

1256866

Banca

CESPE / CEBRASPE

Órgão

INPI

Ano

2013

Provas

CESPE - 2013 - INPI - Tecnologista em Propriedade Industrial

Disciplina

Raciocínio Lógico

Assuntos

Alternativas

Certo

Errado

Comentários

Para analisar reduz-se a frase ao agente e verbo (despreza-se os complementos): Todo governante toma decisões...etc.
Pode ser Falsa (Existe governante que não toma decisões tendo ...) ou Verdadeira.

Portanto, é uma proposição, questão CERTA.
Gabarito: C

Esta frase é uma oração declarativa que pode ser classificada em V ou F.
AO MEU VER..

PROPORÇÃO SIMPLES.
Alguém mais pode contribuir?
CORRETA. e uma proposi;ao pois pode atribuir como VERDADE ou FALSIDADE ela. A nega;ao dela seria Algum governante nao toma decisoes... (nega;ao de todo eh algum nao)

proposi;ao simples, pois expressa uma unica ideia (ideia de governantes tomarem decisoes ou nao), e nao possui conectivos logicos.

(desculpem os erros de digita;ao, teclado desconfigurado)
Certo. Proposição simples. Ùnica idéia.
QUESTAO CORRETA.

TODO = EQUIVALENCIA LOGICA DA PROPOSIÇAO " SE... , ENTAO."
Nem todas as frases são proposições. A saber:

- Sentenças interrogativas;
- Exclamativas;
- Imperativas;
- Sem valor lógico;
- Sem verbo.

Macete:

SEXI SEM LÓVER

--

É estranho, mas acostuma hehe
Proposição atômica( simples)
Proposição molecular ( composta)
silogismo
Exceções das sentenças abertas
Toda sentença que apresente as seguintes expressões:

a) Se ..., então;
b) Todo;
c) Algum, pelo menos um, existe;
d) Nenhum
Questão quase de português:

CASO DIGA A VERDADE, VOCÊ NÃO SERÁ PUNIDO. ORAÇÃO SUBORDINADA ADVERBIAL CONDICIONAL .

DIZENDO A VERDADE, VOCÊ NÃO SERÁ PUNIDO. ORAÇÃO SUBORDINADA ADVERBIAL CONDICIONAL REDUZIDA DE GERÚNDIO.

CONTANTO QUE TENHA COMO principal preocupação sua conservação no poder, TODO governante toma decisões.

Todo governante toma decisões, tendo como principal preocupação sua conservação no poder.

se, caso, desde que, contanto que... etc..
Certo.

Certo – Frase de sentido completo.

Questão comentada pelo Prof. Márcio Flávio
CERTO
Minha contribuição.

Proposição: Pode ser julgada como verdadeira ou falsa.

-Neymar é um péssimo jogador. (proposição)
-Ele é um ótimo desenhista. (não é proposição / sentença aberta)
-Traga o exercício amanhã. (não é proposição / frase imperativa)
-Existe vida após a morte. (proposição)
-Bom dia! (não é proposição / frase exclamativa)
-X + 1 = 4 (não é proposição / sentença aberta)
-2 + 1 = 0 (proposição)
-Qual o seu nome? (não é proposição / frase interrogativa)

Abraço!!!
GAB: CERTA
Sentido completo.

Nem todas as frases são proposições.

- Sentenças interrogativas;

- Exclamativas;

- Imperativas;

- Sem valor lógico;

- Sem verbo

Continue usando...

O que está incluso

+ 2 Milhões de Questões organizadas por assunto
+ 100 Mil Provas de concursos/vestibulares/ENEM
+ 1 Milhão de Questões comentadas
Pague uma única vez e tenha acesso vitalício

Entrar com o Google

📋 PIX COPIA E COLA 📲 Compartilhar PIX via WhatsApp

P	Q	~Q	~P	(P^~Q)	~(P^~Q)	~P^~Q	~(P^~Q)	~Pv~Q	P->Q
V	V	F	F	F	V	F	V	F	V
V	F	V	F	V	F	F	V	V	F
F	V	F	V	F	V	F	V	V	V
F	F	V	V	F	V	V	F	V	V

p	q	¬p	¬q	p ∨ q	¬(p ∨ q)	¬p ^ ¬q
V	V	F	F	V	F	F
V	F	F	V	V	F	F
F	V	V	F	V	F	F
F	F	V	V	F	V	V

PvQ	~ P	(PvQ)^(~ P)
V	V	V
V	F	F
F	V	F
F	F	F

SóProvas