- ID
- 10723
- Banca
- ESAF
- Órgão
- ANEEL
- Ano
- 2004
- Provas
- Disciplina
- Raciocínio Lógico
- Assuntos
Em um grupo de 30 crianças, 16 têm olhos azuis e 20 estudam canto. O número de crianças deste grupo que têm olhos azuis e estudam canto é
Em um grupo de 30 crianças, 16 têm olhos azuis e 20 estudam canto. O número de crianças deste grupo que têm olhos azuis e estudam canto é
Nos Jogos Panamericanos de 1971, na cidade de Cali, um quadro de resultados parciais apresentava os três países com maior número de medalhas de ouro (105, 31 e 19), de prata (73, 49 e 20) e de bronze (41, 40 25): Canadá, Cuba e EUA. Em relação a esse quadro, sabe-se que
- os EUA obtiveram 105 medalhas de ouro e 73 de prata;
- Cuba recebeu a menor quantidade de medalhas de bronze;
- Canadá recebeu um total de 80 medalhas.
Nessas condições, esse quadro informava que o número de medalhas recebidas
Uma pesquisa envolvendo 85 juízes de diversos tribunais
revelou que 40 possuíam o título de doutor, 50 possuíam o título de
mestre, 20 possuíam somente o título de mestre e não eram professores
universitários, 10 possuíam os títulos de doutor e mestre e eram
professores universitários, 15 possuíam somente o título de doutor e não
eram professores universitários e 10 possuíam os títulos de mestre e
doutor e não eram professores universitários.
Com base nessas informações, julgue os itens seguintes.
Menos de 50 desses juízes possuem o título de doutor ou de mestre mas não são professores universitários.
Uma pesquisa envolvendo 85 juízes de diversos tribunais
revelou que 40 possuíam o título de doutor, 50 possuíam o título de
mestre, 20 possuíam somente o título de mestre e não eram professores
universitários, 10 possuíam os títulos de doutor e mestre e eram
professores universitários, 15 possuíam somente o título de doutor e não
eram professores universitários e 10 possuíam os títulos de mestre e
doutor e não eram professores universitários.
Com base nessas informações, julgue os itens seguintes.
Mais de 3 desses juízes possuem somente o título de doutor e são professores universitários.
Uma escola para fi lhos de estrangeiros oferece cursos de idiomas estrangeiros para seus alunos. Em uma determinada série, 30 alunos estudam francês, 45 estudam inglês, e 40, espanhol. Dos alunos que estudam francês, 12 estudam também inglês e 3 estudam também espanhol. Dos alunos que estudam inglês, 7 estudam também espanhol e desses 7 alunos que estudam inglês e espanhol, 3 estudam também francês. Por fi m, há 10 alunos que estudam apenas alemão. Não sendo oferecidos outros idiomas e sabendo-se que todos os alunos dessa série devem estudar pelo menos um idioma estrangeiro, quantos alunos dessa série estudam nessa escola?
Uma pesquisa de opinião foi realizada com 50 pessoas. Essa pesquisa procurava saber que veículos de comunicação (jornal, rádio ou televisão) essas pessoas utilizam para tomar conhecimento das notícias diariamente. Após a pesquisa, descobriu-se que:
41 pessoas utilizam televisão;
33 pessoas utilizam jornal;
30 pessoas utilizam rádio;
29 pessoas utilizam televisão e jornal;
25 pessoas utilizam televisão e rádio;
21 pessoas utilizam jornal e rádio;
18 pessoas utilizam os três veículos.
A quantidade de pessoas que não utilizam nenhum dos três veículos é
A, B e C são três conjuntos. Com base nessa informação, analise as afirmativas a seguir:
I. Se todos os elementos de A pertencem a B, então A e B são o mesmo conjunto.
II. Se A e C não possuem elementos em comum, então um dos dois é um conjunto vazio.
III. Se todos os elementos de A pertencem a B e todos os elementos de B pertencem a C, então todos os elementos de A pertencem a C.
Assinale
No curso de línguas Esperanto, os 180 alunos estudam inglês, espanhol ou grego. Sabe-se que 60 alunos estudam espanhol e que 40 estudam somente inglês e espanhol. Com base nessa situação, julgue os itens que se seguem.
Se 40 alunos estudam somente grego, então mais de 90 alunos estudam somente inglês.
No curso de línguas Esperanto, os 180 alunos estudam inglês, espanhol ou grego. Sabe-se que 60 alunos estudam espanhol e que 40 estudam somente inglês e espanhol. Com base nessa situação, julgue os itens que se seguem.
Se os alunos que estudam grego estudam também espanhol e nenhuma outra língua mais, então há mais alunos estudando inglês do que espanhol.
No curso de línguas Esperanto, os 180 alunos estudam inglês, espanhol ou grego. Sabe-se que 60 alunos estudam espanhol e que 40 estudam somente inglês e espanhol. Com base nessa situação, julgue os itens que se seguem.
Se os 60 alunos que estudam grego estudam também inglês e nenhuma outra língua mais, então há mais alunos estudando somente inglês do que espanhol.
Esta questão esta incorreta porque o número máximo de alunos que poderiam estudar APENAS inglês é 60 e o número de alunos que estudam espanhol é igual a 60 também, ou seja são iguais e não superior.
Não se pode concluir isso, pois não é dado o número de alunos que estudam APENAS grego.
Após análise do gráfico pode-se concluir que:
Alunos que estudam APENAS Inglês = 60
Alunos que estudam APENAS Grego = 00
Contudo a questão não afirma que o número de Alunos que estudam APENAS Inglês é maior do que o que estudam APENAS Espanhol, mas sim dos alunos de espanhol como um todo, o que também é 60. Portanto são iguais e não mais Alunos que estudam APENAS Inglês.
O quantitativo que representa os alunos que estudam "somente inglês"é inferior ao quantitativo que representa "os alunos que estudam espanhol"(20<60).
(conforme disposto no livro CABRAL, Luiz Cláudio; NUNES, Mauro César. Raciocínio Lógico Passo a Passo CESPE. 2ed. p. 309-310)
Entendo essa questão da seguinte forma:
Total: 180
Espanhol: 60
Só inglês e espanhol: 20
Todos os 60 que estudam grego, estudam ingles e nenhuma outra língua.
Com isso, você tem no espaço de somente ingles E grego = 60
A interseção de grego com as outras duas matérias (espaço de interseção triplo), a interseção de somente grego E espanhol, e o espaço de somente grego ficariam zerados (já que todos os 60 que estudam grego estudam somente inglês e nenhuma outra língua).
Prosseguindo o raciocínio, você terá 20 no espaço de somente ingles E espanhol e terá 40 no espaço de somente espanhol (contabilizando os 60 de espanhol).
Somando os valores encontrados teremos:
Somente ingles E grego: 60
Somente ingles E espanhol: 20
Somente espanhol: 40
Total: 120
Sobra dessa forma 60 para somente ingles (180-120).
Ou seja, somente ingles (60) é exatamente igual a espanhol (60).
Questão ERRADA.
Vi pelos comentários que tem gente se confundindo na leitura da questão. Vejam como calculei:
Total de alunos = 180
A ? (inglês)
B 60 (espanhol)
C 60 (grego, subconjunto de A - portanto, nem vamos considerar nos cálculos, pois já está dentro do número dos que estudam inglês)
A/B = 40
C/A = 60
B = 60-40 = 20 (Espanhol total - Espanhol + inglês = Somente Espanhol)
A = 180 - 60 (total de alunos - Espanhol total)
A = 120 (Inglês total)
Quanto é somente inglês? A = 120-40-60 = 20 (A - A/B - B)
Como SOMENTE inglês é 20 e espanhol (não é "SOMENTE", conforme o enunciado) (B) é 60, a resposta é "Errado".
Mesmo que fosse somente espanhol, a resposta estaria, igualmente, errada, visto que os números seriam idênticos (20).
questao confusa, pois nao fala explicitamente que os 20 que estudam espanhol ESTUDAM APENAS ESPANHOL, dentro destes 20 podem ter pessoas que estudem espanhol e grego!!!
questão de português e interpretação, o cerne da questão é a existência da palavra "APENAS" ou a falta da dela.
Entendi da seguinte forma:
Se 60 ficará no campo de somente inglês e grego, o máximo que o campo somente inglês pode chegar é 60, pois 120 já estão distribuídos em espanhol e grego. Como já sabemos que em espanhol é 60 e o campo somente inglês pode chegar no máximo a 60 é impossível que existam mais alunos estudando somente inglês do que espanhol (o máximo que poderia ocorrer é um empate). Por isso, questão errada.
não entendi nada porque na questão pede "Se os 60 alunos que estudam grego"
mas o enunciado diz Sabe-se que 60 alunos estudam espanhol?
me enrolei todo.
TOTAL = 180
ESPANHOL (60) = 20 + 40 >> (inglês ^ espanhol)
Grego (60) = Grego ^ Inglês
-------- até aqui tem um total de 120
-------- falta 60 para fechar os 180
INGLÊS = 40 da interseção com ESP e 60 interseção com GREGO (essa contagem já foi realizada.
GABARITO ERRADO
P: No curso de línguas Esperanto, os 180 alunos estudam inglês, espanhol ou grego:
INGLÊS + ESPANHOL + GREGO (TOTAL) = 180
Q: Sabe-se que 60 alunos estudam espanhol:
ESPANHOL = 60
R: e que 40 estudam somente inglês e espanhol:
INGLÊS + ESPANHOL (INTERSEÇÃO) = 40
S: Se os 60 alunos que estudam grego estudam também inglês e nenhuma outra língua mais:
INGLÊS + GREGO (INTERSEÇÃO) = 60
Pergunta: "então há mais alunos estudando somente inglês do que espanhol.", OU SEJA, QT DE ALUNOS DE INGLÊS > QT DE ALUNOS DE ESPANHOL?
Temos que descobrir a quantidade de alunos somente em inglês, então: Q - R = 20.
COM ISTO SABEMOS QUE:
ALUNOS DE INGLÊS (20) > ALUNOS DE ESPANHOL (60)?
ERRADO
ING= 60
ING~ESP= 40
ESP= 20
ING~GRE=60
GRE=0
Com os dados fica facíl saber que somente ing é igual ao todo esp, porém, é necessário uma interpretação de texto " então há mais alunos estudando somente inglês do que espanhol". Na primeira leitura eu achei que tinha um "somente" antes de espanhol em estado elíptico, o que consideraria a questão errada.
Em uma escola que tem 415 alunos, 221 estudam inglês, 163 estudam francês e 52 estudam ambas as línguas. Quantos alunos não estudam nenhuma das duas línguas?
Tem 415 alunos, então :
Alunos - 415
Inglês - 221
Francês - 163
Ambas - 52
Então é só fazer :
415 - 221 = 194
194 - 163 = 31
31 + 52 = 83
Logo a alternativa correta e a letra C
Bons Estudos !!
Total=I+F-(I+F)+x
Nota-se:(I+F) interseccao de I e F , ou seja estuda as duas linguas e x sao os alunos que nao estuda nenhuma lingua.Entao:
415=221+163-52+x===>x=83
alunos- 415
inglês- 221
francês- 163
ambas- 52
nenhuma- x 221+163 = 384
384-52 = 332
332-415 = 83
X=83 letra C
Total = 415
Ing = 221
fran = 163
Ing e Fran = 52
221 - 52 = 169
163 - 52 = 111
Soma os resultados = 52 + 169 +111 = 332
Subitraímos o total (415) - 332 = 83
Pessoal, só uma perguntinha que ainda não entendi.
Se no total são 384 (221+163) alunos que estudam alguma língua, independente se é ingles ou frances ou as duas, como podem haver 83 alunos que não fazem lingua alguma, se o total de alunos é 415? (384+83 = 467)
Ou então = como a questão nos pergunta "quantos não fazem lingua alguma", temos que verificar quem sobra.
Para mim a conta é a seguinte:
221 - ingles
163 - frances
52 - fazem as duas linguas (já incluidos no 221 e no 163)
415 - total de alunos
415 - 384 = 31 alunos que não fazem lingua alguma
Aí alguém vai dizer que esqueci de subtrair 52 de 221 e 52 de 163.
Mas aí não seriam mais 52 alunos que fazem as duas linguas e sim 104, pois tiramos 52 de 221 MAIS 52 de 163...
Sei que parece confuso, mas com certeza muita gente está vendo este resultado na internet e apenas aceitando este resultado como certo e até agora não me convenci de que está certo.
Algum professor poderia esclarecer, por favor??
Na verdade não. Pensa o seguinte: Quando o enunciado diz 221 ingles e 163 frances ele não usa a palavra "somente" ingles nem "somente" frances. Imagina o seguinte, vc é uma dessas alunas que sabem as duas linguas. Vc está sendo contada no ingles e no frances. Logo, se somarmos 163 + 221+ 52, estamos contando vc TRES vezes. Veja, nesse caso, vc está no Grupo 163, no grupo 52 e no grupo 221. Como vc é apenas uma pessoa, só pode estar em UM grupo. No caso, seu grupo é o 52 e para garantir que vc seja contada SOMENTE no 52 fazemos uma subtração desse grupo. E pq subtraimos nos dois? Pensa, se vc está sendo contada TRES vezes e queremos contá-la apenas uma vez, subtraimos tanto no frances como no ingles. Perceba, quando o enunciado utilizar a palavra "somente", ele está dizendo que, esse grupo é homogêneo e não está sendo contabilizado nada mais, no caso, o enunciado não disse nada, então devemos sempre subtrair o conjunto maior da interseção. Nas questões de conjuntos, comece sempre preenchendo a(s) interseções, sempre assim.
Inglês: 221
Francês: 163
Inglês e Francês: 52
Somente Inglês: 221 - 52 = 169
Somente Francês: 163 - 52 = 111
Logo, a soma dos que cursam SOMENTE inglês, somente francês e os que cursam os dois, é o número de alunos que estudam as duas línguas (332). Daí, é só subtrair pelo número total de alunos (415) para achar o resultado da questão. 83.
GABARITO: C
O mais difícil é resolver isso por análise combinatória
Total = 415
(Inglês) = 221
(Francês) = 163
(Inglês e Francês) = 52
Inglês puro = (Inglês) - (Inglês e Francês) = 169 - 52 = 169
Francês puro = (Francês) - (Inglês e Francês) = 163 - 52 = 111
Soma tudo = Inglês puro + Francês puro + (Inglês e Francês) = 332
Total - Soma tudo = 415 - 332 = 83
Alternativa (C)
Um grande abraço e bons estudos :)
Resolver por conjunto é melhor.
169- 52+163-52+52+X=415
X=83
Resposta: 83 C
Por conjuntos é simples pois ele concede quem estuda ambas as linguas que é 52:
-415 alunos
- 221 estudam inglês - 52 que estudam francês e inglês= 169
-163 estudam francês - 52 que estudam também francês e inglês= 111
soma 169+52+111=332 que é o total de alunos que estudam francês, inglês e ambas as linguas.
415- 332= 83 alunos não estudam nenhuma dessas linguas, Gabarito C)
Acredito que essa questão esteja classificada errada
Deveria ser em "diagramas de venn" ( resolvi assim)
minha opinião
Um colégio oferece a seus alunos a prática de um ou mais dos seguintes esportes: futebol, basquete e vôlei. Sabe-se que, no atual semestre,
- 20 alunos praticam vôlei e basquete;
- 60 alunos praticam futebol e 65 praticam basquete;
- 21 alunos não praticam nem futebol nem vôlei;
- o número de alunos que praticam só futebol é idêntico ao número dos alunos que praticam só vôlei;
- 17 alunos praticam futebol e vôlei;
- 45 alunos praticam futebol e basquete; 30, entre os 45, não praticam vôlei.
O número total de alunos do colégio, no atual semestre, é igual a
Não sei inserir o desenho, então vou passar o número de estudantes em cada esporte:
somente vôlei: 13
somente basquete: 15
somente futebol: 13
vôlei e basquete: 5
basquete e futebol: 30
vôlei e futebol: 2
vôlei, futebol e basquete: 15
nenhum esporte: 6
Bons estudos.
como vcs chegaram a conclusão de que os que não praticam nenhum esporte são 6?????
Ola Lílian!
Reposta:
http://beijonopapaienamamae.blogspot.com/2010/10/dia-05-de-outubro-questao-278.html
Essa questão me deu trabalho.
Dá pra entender de cara que:
V + F = 20
F + B = 45
F + V = 17
Pra mim o primeiro segredo foi quando ele disse que 30 entre os 45 Futebol + Volei, não praticavam Basquete, sendo então 15 a interseção dos três conjuntos.
A partir daí:
VB = 20 - 15 = 5
FV = 17 - 15 = 2
FB = 45 - 15 = 30
Como ele deu o numero de Basquete e Futebol é só subtrair e achar que
Apenas Basquete = 15
Apenas Futebol = 13
Apenas volei ele disse na questão que era igual ao número de apenas futebol = 13
O segundo lance é que ele diz que 21 não faz nem futebol, nem volei (Mas não cita o Basquete). Logo pra achar os que não fazem nada é só diminuir dos que fazem apenas basquete = 21 - 15 = 6
Aí agora é somar tudo: 13 (F) + 2 (FV) + 30 (FB) + 15 (FVB) + 15 (B) + 5 (VB) + 13 (V) + 6 (Não faz nada) = 99
a sobra dos 6 nenhum esporte que me pegou referente aos 21 -15 do basquete
Foi observado que uma loja de departamentos recebe, por hora, cerca de 250 clientes. Destes,
. 120 se dirigem ao setor de vestuário;
. 90, ao setor de cosméticos;
. 80, ao setor de cinevídeo;
. 50, se dirigem aos setores de vestuário e de cosméticos;
. 30, aos setores de cosméticos e de cinevídeo e
. 30, aos setores de vestuário e cinevídeo.
Observou-se, ainda, que 50 clientes se dirigem a outros setores que não vestuário ou cosméticos ou cinevídeo. Qual a probabilidade de um cliente entrar nessa loja de departamentos e se dirigir aos setores de vestuário, de cosméticos e de cinevídeo ?
A banca quer saber qual é a probabilidade de um cliente entrar nessa loja de departamentos e se dirigir aos setores de vestuário, de cosméticos e de cinevídeo. Assim, segue a análise:
• 50 clientes se dirigem a outros setores que não vestuário ou cosméticos ou cinevídeo, ou seja, esses 50 clientes não participam de nenhum dos três conjuntos;
• Chamaremos de X a interseção entre ambos os conjuntos, assim temos que:
• Pessoas que se dirigem somente aos setores de vestuário e de cosméticos = 50 – X
• Pessoas que se dirigem somente aos setores de cosméticos e de cinevídeo = 30 – X
• Pessoas que se dirigem somente aos setores de vestuário e cinevídeo = 30 – X
Com isso, para descobrir outras partes do conjunto, temos:
Para o conjunto A: VESTIÁRIO
120 – (80 – X)
120 – 80 + X
40 + X
Para o conjunto B: COSMÉTICO
90 – (80 – X)
90 – 80 + X
10 + X
Para o conjunto C: CINEVÍDEO
80 – (60 – X)
80 – 60 + X
20 + X
Assim, para encontrar o valor de X, basta somar todos os conjuntos e igualar a 200. Veja:
40 + X + 50 - X + 10 + X + X + 30 – X + 30 – X + 20 + X = 200
40 + 50 + 10 + 30 + 30 + 20 + X = 200
40 + 50 + 10 + 30 + 30 + 20 + X = 200
180 + X = 200
X = 200 – 180
X = 20
Como o examinador quer saber a probabilidade de um cliente entrar nessa loja de departamentos e se dirigir aos setores de vestuário, de cosméticos e de cinevídeo, basta fazer o seguinte cálculo:
P= 20/250=0,08
Resposta: A
Em um grupo de 100 pessoas, sabe-se que:
? 15 nunca foram vacinadas;
? 32 só foram vacinadas contra a doença A;
? 44 já foram vacinadas contra a doença A;
? 20 só foram vacinadas contra a doença C;
? 2 foram vacinadas contra as doenças A, B e C;
? 22 foram vacinadas contra apenas duas doenças.
De acordo com as informações, o número de pessoas do grupo que só foi vacinado contra ambas as doenças B e C é
OS conjuntos formados ficam assim
Somente A - 32
Somente AB - 5
Somente AC - 5
ABC - 2
Somente B - 9
Somente BC - 12
Somente C - 20
Resto - 15 -------------- Total = 100
Considerando que o grupo de pessoas vacinadas contra a doença A (44) é formado por pessoas:
- Vacinadas somente contra A: 32
- Vacinadas contra A e B: ?
- Vacinadas contra A, B e C: 2
- Vacinadas contra A e C: ?
Temos que o grupo AB e AC é constituído por:
AB + AC = 44 - 32 - 2 = 10 pessoas.
Mas, conforme o enunciado, as pessoas vacinadas contra duas doenças, ou seja, AB + BC + AC, são 22, então:
AB + AC + BC = 22 ==> 10 + BC = 22 ==> BC = 12 pessoas.
Portanto, alternativa correta "b".
Admita as frases seguintes como verdadeiras.
I. Existem futebolistas (F) que surfam (S) e alguns desses futebolistas também são tenistas (T).
II. Alguns tenistas e futebolistas também jogam vôlei (V).
III. Nenhum jogador de vôlei surfa.
A representação que admite a veracidade das frases é:
Analisemos cada uma das preposições, pois esse exercicio deve ser feito por exclusão das demais:
Pelo item número I podemos excluir as letras "B", porque não há surfistas futebolistas no diagrama e "E", porque todos os futebolistas também são tenistas e não "alguns" e também porque nenhum futebolista surfa;
Pelo item número II podemos excluir as letras "D", porque os que são futebolistas não jogam volei;
Pelo item número III podemos excluir a letra "C", porque há jogadores de volei que surfam.
Bons estudos
Questão simples de Diagramas Lógicos.
Basta testar as afirmações e verificar se há as interseções explicitadas na questão.
Resposta certa:
LETRA A.
Bons estudos!
Pelo enunciado da questão, já podemos eliminar de pronto as alternativas C, D e E, pois não há interseção entre o conjunto dos que jogam vôlei e o conjunto dos que surfam. Ficamos então entre a letra A e B. Vejamos:
No enunciado temos: "I. Existem futebolistas (F) que surfam (S) e alguns desses futebolistas(futebolistas que surfam) também são tenistas (T). "Este item está nos informando que há futebolistas que surfam e também são tenistas, ou seja, há interseção entre os três conjuntos, mas a letra B não representou no diagrama.Ficamos então com a letra A.
Explicação em vídeo: https://www.youtube.com/watch?v=i3ygf4nn0H8
Considere que, em uma amostra composta por 210 pessoas atendidas em unidade de atendimento do DETRAN, 105 foram ao DETRAN para resolver pendências relacionadas à documentação de veículos; 70, para resolver problemas relacionados a multas; e 70, para resolver problemas não relacionados à documentação de veículos ou a multas. A respeito dessa situação hipotética, julgue o item.
Em face dessa situação, é correto afirmar que, nessa amostra, menos de 30 pessoas procuraram a unidade de atendimento do DETRAN para resolver problemas relacionados simultaneamente à documentação de veículos e a multas.
o diagrama deve conter 3 conjuntos: MULTA, DOCUMENTOS E OUTROS.
O que se pode afirmar sobre o problema é que, o número de pessoas que que foram ao Detran devido a MULTA e DOC, foi igual OU MENOR do que 35 pessoas, (pois nada se pode inferir quanto às pessoas que foram resolver coisas de 3 classificações ou de 2 classificações. Mas o número é menor que 35).
Para resolver essa questão vamos usar alguns conceitos básicos sobre Conjuntos. Usando os conjuntos Documentação, Multas e Outros, a única certeza que temos é que 70 pessoas não foram tratar nem de documentação e nem de multas. Além disso, do contexto podemos assumir que as pessoas que foram resolver problemas de documentação ou de multas não foram também resolver outras coisas, mas pode haver pessoas que foram resolver problemas de documentação e de multas também. Assumindo que X pessoas foram resolver problemas de documentação e de multas, temos que 105 – X foram resolver apenas problemas de documentação, e 70 – X foram resolver apenas problemas de multas:

Portanto, podemos dizer que:
210 = 70 + (105 – X) + X + (70 – X)
210 = 245 – X
X = 35 pessoas
Assim, mais de 30 pessoas foram resolver problemas de documentação e também de multas. Item ERRADO
Se vc considerar que são eventos independentes ,vc tem que 105/210 que é 1/2, foram pra docunentos, e 70/210 que é 1/3 foram pra multas ,aí como é independente (1/2)x(1/3) da 1/6 ,ou seja 1/6 foram pra resolver multas e documentos , 1/6 de 210 da 35
Errado. 105+70=175 210-175= 35 resposta.
35 pessoas foram resolver os dois problemas.
Conversando com os 45 alunos da primeira série de um colégio, o professor de educação física verificou que 36 alunos jogam futebol, e 14 jogam vôlei, sendo que 4 alunos não jogam nem futebol nem vôlei. O número de alunos que jogam tanto futebol quanto vôlei é
45 - 4 = 41 (alunos que jogam algum esporte)
41 - 36 = 5 (alunos que jogam apenas vôlei)
41 - 14 = 27 (alunos que jogam apenas futebol)
5 + 27 = 32 (alunos que jogam apenas vôlei ou apenas futebol)
41 - 32 = 9 (alunos que jogam tanto vôlei quanto futebol)
Somei todos os alunos 36 + 14 + 4 = 54
Como são 9 a mais dos 45 com quem o professor conversou, concluí que seria a resposta.
Interseção ...
T = 45
F = 36
V = 14
Nenhum = 4
F e V = ??
36 + 14 + 4 = 54
54 - 45 = 9
F e V = 09
SE DOS 45 ALUNOS 4 NAO JOGAM, ENTÃO 45 -4= 41 É O TOTAL D ALUNOS Q PARTICIPAM DAS ATIVIDADES ESPORTIVAS
14 JOGAM VOLÊI, 36 FUTEBOL,ENTÃO 14 MAIS 36= 50
AGORA SÓ SUBTRAIR = 50-41= 9
GABARITO: LETRA C
Total = 45
Futebol = 36
Vôlei = 14
Nenhum = 4
Futebol e vôlei = ?
Futebol + vôlei + nenhum = 54
54 – 45 (total) = 9
PROF º LUIS TELLES - GRAN CURSOS
Macete : quando pedir o valor da interseção ,basta somar tudo e subtrair do total.
Logo : 14 + 36 + 4 = 54
54 - 45 = 9
--------------------------------------------------------------------------------------------------------
O segredo do sucesso é nunca desistir !!!
SOMA TUDO E SUBTRAI PELO TOTAL DE ALUNOS
36 + 14 + 4
= 54
54 - 45
= 9
Dados fornecidos pelo item:
• 45 alunos da primeira série de um colégio;
• 36 alunos jogam futebol;
• 14 jogam vôlei;
• 4 alunos não jogam nem futebol nem vôlei.
A banca quer saber o número de alunos que jogam tanto futebol quanto vôlei, ou seja, a interseção entre os conjuntos. Assim, segue a análise:
• 4 alunos não jogam nem futebol nem vôlei, ou seja, esses 4 alunos não participam de nenhum dos dois conjuntos;
• Chamaremos de X a interseção entre ambos os conjuntos, assim temos que:
• Alunos que jogam somente futebol = 36 – X
• Alunos que jogam somente vôlei = 14 – X
• Assim, para calcular o valor de X, que representa o número de alunos que jogam tanto futebol quanto vôlei, basta fazer o seguinte cálculo:
36 – X + X + 14 – X + 4 = 45
36 + 47 – X +4 = 45
54 – X = 45
– X = 45 – 54
– X = - 9
X = 9
A seguir encontra-se a representação em forma de conjuntos:
Resposta: C
45 - 4 = 41
41 - 36 = 5
41 - 14 = 27
27 + 5 + 4 = 36
45 - 36 = 9
Acerca de operações com conjuntos, julgue o item subsequente.
Considere que os conjuntos A, B e C tenham o mesmo número de elementos, que A e B sejam disjuntos, que a união dos três possuia 150 elementos e que a interseção entre B e C possuia o dobro de elementos da interseção entre A e C. Nesse caso, se a interseção entre B e C possui 20 elementos, então B tem menos de 60 elementos.
GALERA, CONSEGUIR ACHANDO TODOS OS ELEMENTOS DISJUNTOS ENTRE SI.!!!!
A+B+C= 150
B^C= 20
A^C= 10
LOGO, SOMANDO ESSAS 2 INTERSEÇÕES, PODEMOS CONCLUIR QUE C TEM 30 ELEMENTOS DISJUNTOS DOS DEMAIS.
ENTÃO:
C = 30
A= ?
B= ?
150-30= 120. PORTANTO, A+B TEM QUE DAR 120. E SE A e B SÃO DISJUNTOS EM SEU TOTAL, LOGO PODEMOS CONCLUIR QUE CADA ELEMENTOS TERÁ A METADE DE 120. OU SEJA, 60.
FICANDO, PORTANDO: TODOS DISJUNTOS EM:
A= 60
B= 60
C= 30
TOTAL A+B+C= 150.
COM ISSO CHEGAMOS A CONCLUSÃO QUE B TEM 60 E NÃO MENOS!!!!
B= 60 GABARITO ERRADO!!!!!
ESPERO TER CONTRIBUÍDO UM POUCO!!!!!!
Prof. Ivan chagas. RESPOSTA
youtube.com/watch?v=DPZFrC1i4uc
AUBUC = A + B + C - A^C - A^B - B^C + A^B^C
150 = X + X + X - 10 - 0 - 20 + 0
150 = 3X - 30
3X = 180
X = 60
QUESTÃO SIMPLES.
A
B
C
A QUESTÃO DIZ QUE O TRIO SÃO IGUAIS.
150 É A INTERSEÇÃO (a, b e c)
20 B e C
10 é A e C, pois diz que B e C é o dobro de A e C
soma: 150+20+10=180
depois divide por 3 que é EXATAMENTE 60, e não menos que 60.
GAB E
se colocar na formula da certo, no entanto não entendi , pois ele fala que os TRÊS CONJUNTOS TEM 150, então quando o pessoal ai somam os 20 e os 10 com 150, para mim estaria duplicando, pois os 150 já estão incluso os 10 e 20.
resumindo :os 150 já sao o total junto com as interseções .
Olá pessoal,
Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/DPZFrC1i4uc
Professor Ivan Chagas
www.youtube.com/professorivanchagas
Excelente questão.
Sem complicar.
Interseção de B e C = 2X ou X
Interseção de A e C = X ou X/2
A questão informou que B e C têm 20 elementos, portanto, A E C têm 10 elementos.
Prosseguindo, a questão informou que os conjuntos têm o mesmo número de elementos, então:
A + B + C - 10 - 20 = 150 (lembrando que - com - é +, permanecendo o sinal do maior)
A + B + C - 30 = 150
A + B + C = 150 + 30
A + B + C = 180
Como tem o mesmo número de elementos, é só dividir 180 por 3.
180/3 = 60
Ou seja, o conjunto B tem exatamente 60 elementos.
Galera, vamos fazer os seguintes sistemas:
A + B + C + 30 = 150 (Os 30 se referem a interseção dado pela questão)
A+10 = B+20 (Esses valores são da interseção)
B+20 = C+30
A+10 = C+30
Agora é só isolar os termos, de modo que vc use apenas uma letra na equação principal, e após descobrir ela vc descobre as demais... Foi assim que eu fiz e deu certo. O resultado deu B=50, C=40 e A=50.
Considere que todos os 80 alunos de uma classe foram levados para um piquenique em que foram servidos salada, cachorro-quente e frutas. Entre esses alunos, 42 comeram salada e 50 comeram frutas. Além disso, 27 alunos comeram cachorro-quente e salada, 22 comeram salada e frutas, 38 comeram cachorro-quente e frutas e 15 comeram os três alimentos. Sabendo que cada um dos 80 alunos comeu pelo menos um dos três alimentos, julgue o próximo item.
Quinze alunos comeram somente cachorro-quente.
TOTAL 80 ALUNOS
42 salada -12-07-15=08 só salada
50 frutas -07-23-15=05 só frutas
27 cachorro e salada -15=12
22 salada e frutas -15=07
38 cachorro e frutas -15=23
15 comeram os 3
só cachorro quente = 80 -08-05-12-07-23-15= 10 alunos
Vou chamar de S = salada, C = cachorro-quente, F = frutas, ^ = intersecção e v = união
S ^ C = 27
S ^ F = 22
C ^ F = 38
S ^ F ^ C = 15
Note que a intersecção entre os três conjuntos(desenhe o diagrama) é 15, portanto esse "15" já está incluído na intersecção de "S ^ C", "S ^ F" e "C ^ F", com isso precisaremos diminuir, ou seja:
27 - 15 = 12
22 - 15 = 7
38 - 15 = 23
Esses valores "12", "7" e "23" são meus valores reais da intersecção dos conjuntos "S ^ C", "S ^ F" e "C ^ F", agora basta diminuir do número de pessoas que comeram SALADA = 42 e FRUTAS = 50 para sabermos realmente quantos comeram SÓ SALADA e SOMENTE FRUTAS.
SALADA = 42 - 12 - 15 - 7 = 8 pessoas comeram somente salada
FRUTAS = 50 - 23 - 15 - 7 = 5 pessoas comeram somente frutas
Agora ficou fácil né, basta somar os resultados obtidos, ou seja, nossa verdadeira intersecção e as pessoas que comeram somente salada e somente frutas para assim sabermos quantas comeram cachorro-quente:
Total = intersecções( 12 + 15 + 7 + 23) + salada( 8 ) + frutas( 5 ) = 70, como o total é n=80 deduzimos que 10 pessoas comeram cachorro-quente, e não quinze como a questão havia afirmado!
Abraço!!
Simples, basta aplicar o Princípio da Inclusão e Exclusão. Colocarei a fórmula para 3 elementos.
CvFvS = (C+F+S)-( C^F+C^S+S^F)+(C^F^S)
80= C +50+42- (22+27+38)+(15)
80= C + 107-87
C= 60 alunos
Raramente cai em concursos 4 elementos, deixarei a fórmula:
AvBvCvD = (A+B+C+D)-( A^B+A^C+A^D+B^C+B^D+C^D)+(A^B^C+A^B^D+B^C^D+ C^D^A)-( A^B^C^D)
Fórmula Geral:
União todos elementos= Cn,1(Somatório um a um)- Cn,2(somatório da interseção dois a dois)+Cn,3(somatório da interseção três a três) -...-Cn,n-1(somatório da interseção n a n)
Só eu fiz utilizando diagramas de Venn? rsrsrs
Fiz pelo diagrama de Venn. Apenas 10 comeu cachorro quente.
Tbm fiz pelo diagrama e deu 10.
GABARITO: ERRADO.
Fiz o diagrama de Venn e o resultado foi que apenas 10 alunos comeram cachorro quente.
BONS ESTUDOS!
Acho questões de diagrama tão gostosinhas!
Pessoal, no diagrama fica mais fácil para resolução, mas vou tentar explicar passo a passo.
UNIVERSO = 80 alunos CONJUNTO = cachorro-quente e frutas. SBCONJUNTOS:
42 comeram salada50 comeram frutas
27 alunos comeram cachorro-quente e salada
22 comeram salada e frutas
38 comeram cachorro-quente e frutas
15 comeram os três alimentos
_____________________________________________________________________________________________________________
Comecei de baixo para cima
15 é a interserção dos três conjuntos
38 -15 = 23 comeram CQ e FR
22-15 = 07 comeram SL e FR
27 - 15 = 12 comeram SL e CQ
Observem que o enunciado apresenta o total de pessas que comeram salada(42) e fruta (50)
Salada = 42 - 34 = 08
Mostrando a soma dos elementos do sbconjunto de quem comeu salada(8+12+15+7 = 42)
Fruta = 50 - 45 = 05
Mostrando a soma dos elementos do subconjunto de quem comeu fruta ( 7+15+23+5 = 50)
Cachorro quente = x - 50
x é igual ao número de pessoas que comeram só cachorro - quente.
____________________________________________________________________________________________________________
Bom ,aqui eu peguei todos os elementos dos subconjuntos e somei
---> 15 + 23 + 7 + 12 + 8 + 5 = 70
80 (UN) -70 (SB) = 10 alunos
Assim o x é igual a 10, portanto gabarito errado.
TOTAL = 80
42 - salada
50 - fruta
27 - cachorro e salada
22 - salada e fruta
38 - cachorro e fruta
15 - todos (premissa)
1º
cachorro e salada ► 27-15 = 12
salada e fruta ► 22-15 = 7
cachorro e fruta ► 38-15 = 23
2º
salada ► 42-15-12-7 = 8 (só salada)
fruta ► 50-15-7-23 = 5 (só fruta)
3º
só cachorro ► 80-15-12-7-23-8-5= 10
S,c, f= 15
S e c = 27-15= 12
S e f = 22-15=7
C é f = 38-15=23
Só s = 42 - (15+12+7)= 8
Só f= 50 - (15+7+23)=5
Só c= x -(15+12+23) = x- 50
C= x-50
calculo de X
80= 15+12+7+23+8+5+x-50( soma tudo)
X= 60( ainda não temos c)
C= x -50
C = 60-50 =10, este é o valor de c(10)
gabarito errado
gabarito errado
RESOLUÇÃO: http://sketchtoy.com/69303659
Vídeo super explicativo: https://www.youtube.com/watch?v=IMfl8BXZTv4
Considere que todos os 80 alunos de uma classe foram levados para um piquenique em que foram servidos salada, cachorro-quente e frutas. Entre esses alunos, 42 comeram salada e 50 comeram frutas. Além disso, 27 alunos comeram cachorro-quente e salada, 22 comeram salada e frutas, 38 comeram cachorro-quente e frutas e 15 comeram os três alimentos. Sabendo que cada um dos 80 alunos comeu pelo menos um dos três alimentos, julgue o próximo item.
Sessenta alunos comeram cachorro-quente.
Obrigada Garofolo! Tinha respondido 10 ..
mas percebi que que a banca não pediu APENAS o cachorro quente..
e sim todos que comeram o cachorro quente ;)
GABARITO: CERTO
80 alunos, sendo que:
15 comeram os três alimentos
07 comeram apenas salada e fruta
23 comeram apenas cachorro-quente e fruta
12 comeram apenas salada e cachorro-quente
08 comeram apenas salada
05 comeram apenas fruta
___
70
80 - 70 = 10 alunos comeram apenas cachorro-quente;
15 + 23 + 12 + 10 = 60 alunos que comeram cachorro-quente.
Bons estudos!
Errei porque achei 10 que comeram APENAS cachorro-quente. Ao reler a questão vi que me enganei. A questão perguntava quem comeu cachorro-quente e não quem comeu apenas. O lugar de errar é aqui!!! rs
Analisando-se a situação administrativa de cada um dos 84 funcionários de uma empresa, verificou-se que 68 funcionários fizeram o exame médico anual, 52 tomaram a vacina de gripe (sugerida pela empresa) e 13 não fizeram exame médico nem tomaram a vacina. O número de funcionários que fizeram o exame e tomaram a vacina é de
T= 84
Exame médico anual = 68
Tomaram vacina= 52
Nenhum dos dois = 13
Os dois= ??
68+52+13= 133-84=49
84-13=71
68+52=120
120-71= 49
Gabarito: e
--
68 + x + 52 + 13 = 84
133 + x = 84
x = 84-133 = 49
errei
COMO O QUE A QUESTÃO PEDE É A INTERSECÇÃO , OU SEJA , QUEM TOMOU A VACINA E QUEM FEZ O EXAME , BASTA :
EX + VAC + NENHUM DOS DOIS - TOTAL =
68 + 52 + 13 - 133 = 49
SE OPTAR POR TIRAR O " NENHUM DOS DOIS " DO TOTAL TEMOS O MESMO VALOR :
TOTAL - NENHUM =
84 - 13 = 71
EX + VAC - 71 =
120 - 71 = 49
ESQUECE ESSE NEGÓCIO DE X. É BEM SIMPLES:
Passo 1) Pega o total e diminui os que não fizeram nada (84-13= 71).
Passo 2) Soma quem fez algo (68 exame + 52 vacina = 120)
Passo 3) Subtrai os que fizeram algo pelo resultado do passo 1. (120 - 71 = 49)
PMCE
Basta somar os dados e subtrair pelo total. 68 + 52 + 13 = 133 - 84 = 49
ainda foi generosa por não ter colocado 36 nos itens
Determinada instituição de ensino pretende criar um time
de basquete, para representá-la nos jogos estaduais, que será
formado por uma comissão técnica constituída por um treinador, um
assistente e doze atletas. Após o período de divulgação do time e
das inscrições, cinco pessoas candidataram-se para a comissão
técnica e quinze jovens mostraram interesse em se tornar atletas
desse time.
Para completar o processo, será realizada uma enquete
com cem alunos dessa instituição, com a finalidade de escolher as
cores desse time. A cédula de votação apresenta como opções a cor
verde e a azul, sendo permitido o voto em uma cor, em ambas as
cores ou o voto em branco.
Com base nessas informações, julgue os itens a seguir.
Se, na enquete, 28 alunos votarem em branco, 15, nas duas cores e 47, na cor verde, então mais de 20 alunos votarão apenas na cor azul.
Verde= 32
duas cores =15
Branco= 28
só azul= 25
32+15+28= 75
75-100= 25
Verde + Azul: 15
Só Verde: 47 - 15 (32)
Branco: 28
Azul: X
100 - 28 - 32 - 15 = 25 pessoas votaram apenas no azul.
Em uma classe de 20 alunos, foi realizada uma pesquisa de
opinião relativa às práticas de futebol e de vôlei. Do total de alunos da
classe, 5 afirmaram praticar apenas vôlei e 9 afirmaram praticar futebol.
De acordo com a situação exposta no texto, o número de alunos que não praticam vôlei nem futebol é igual a
TOTAL = 20
5 V
9 F
+-------------
14 20
-14
-------------
06
5 + 9 = 14
20 - 14 = 6
A CESPE faz tantas pegadinhas que até duvidei da facilidade desta questão.
A questão é fácil agora por causa da calma que temos em casa. Na hora da prova, a questão fica duvidosa em razão do medo. O medo amplia a sombra na parede.
Tão fácil que chega a ser duvidosa.
Fácil neh? mas teve gente que errou!
Tenha humildade você que ACERTOU!
Aos que erraram façam o diagrama na tranquilidade que você não erra! :)
clica no link e veja: https://sketchtoy.com/69360152
Nessa questão poderia fazer o seguinte( Deu certo)
n(A)+n(B)-n(A^B)/2 ......Pq são duas modalidades
9+5= 14
14-2=12
12/2=6
Hummmmm suspeito
Obs. no "apenas" toda vez que aparecer só repete o valor.
TOTAL=20
F=3
V=5
INTERSEÇAO=6
NENHUM= 6
20-14 = 6
Questão tranquilo, mas pela fama da banca duvidei da facilidade.
Em uma classe de 20 alunos, foi realizada uma pesquisa de
opinião relativa às práticas de futebol e de vôlei. Do total de alunos da
classe, 5 afirmaram praticar apenas vôlei e 9 afirmaram praticar futebol.
Considerando a situação apresentada no texto, se exatamente 2 alunos praticam tanto futebol quanto vôlei, então o número de alunos que praticam exclusivamente futebol é igual a
5+9 = 14
14/2 (alunos) = 7
Apenas Volei = 5
Volei e futebol = 2
Futebol = 2 - 9 = 7
Você está confundindo com Consórcio Público. A questão trata de consórcio Administrativo.
Uma reportagem sobre “Comportamento no Trânsito” foi feita por um jornal de grande veiculação em uma determinada cidade brasileira. Nessa reportagem, foi feito um teste com 120 pessoas para entender como seriam suas reações diante de uma situação de risco no trânsito. O teste obteve os seguintes resultados:
– 60% das pessoas responderam que, quando o celular toca, logo atendem;
– 50% das pessoas responderam que nunca dirigem após a ingestão de bebida alcoólica; e
– 30% das pessoas responderam que atendem ao celular e nunca dirigem após ingerirem bebida alcoólica.
A partir desses dados, é correto a?rmar que
gabarito letra A
diagrama http://sketchtoy.com/69205564
A) 96 pessoas atendem ao celular ou não ingerem bebida alcoólica se forem dirigir.
➡ o ou representa união de conjuntos, o e representa a interseção
ou seja, ele pede AuB = 80%
80% de 120 = 96
bons estudos
120 (total de pessoas) = 60% de 120 (72 pessoas atendem) + 50% de 120 ( 60 pessoas não dirigem) - 30% de 120 ( 36 pessoas, intersecção de pessoas que atendem e não dirigem) + ALGUM RESTO.
Temos então ==> 120 = 72 + 60 - 36 + X ----> X = 24 total de pessoas que não respondeu nada.
Logo 96 pessoas responderam
24 não responderam
96 atendem OU não bebem
Se algo estiver equivocado avisem, valeu!
Considere que uma pesquisa de mercado tenha sido realizada na cidade de Parintins. Após o resultado, veri?cou- se que 1.000 pessoas usavam dois tipos de cremes dentais branqueadores, denominados E ou F; que o creme dental F é usado por 400 pessoas; e que 160 usam os dois cremes.
Assinale a opção que apresenta o número de pessoas que usam apenas o creme dental E.
QUESTÃO GRANDE LATE, MAS NÃO MORDE.
GABARITO B
VEJA!
160 usam os dois FICA DE FORA, VISTO QUE ELE DESEJA APENAS o creme dental E
1000-400=600
Considere que, de um grupo de 75 servidores do governo municipal de Manaus, 16 servidores relataram em uma pesquisa que gostam de música, esportes e viagens como lazer; 24 gostam de música e esporte; 30 gostam de música e viagens; 22 gostam de esportes e viagens; 7 gostam somente de música; 9, somente de esporte; e 4, somente de viagens.
Assinale a opção que apresenta a possibilidade de, ao acaso, um desses servidores gostarem de música.
Considere ^ interseção.
16 servidores relataram em uma pesquisa que gostam de música, esportes e viagens como lazer;
24 gostam de música e esporte;
30 gostam de música e viagens;
22 gostam de esportes e viagens;
7 gostam somente de música;
9, somente de esporte;
4, somente de viagens.
Como já sabemos o total basta achar os valores correspondentes ao Conjunto música.
M^E^V = 16
M^E = 24 - 16 (descobriremos quantos gostam apenas de musica e esporte) = 8
M^V = 30 - 16 (mesma ideia acima) = 14
M = 7 Como a questão diz que "somente" não é preciso remover as interseções para achar o valor real.
Para achar a quantidade total dos servidores que gostam de música somamos os valores encontrados acima.
16(Música, viagem e esporte) + 8(Música e esporte) + 14(Música e viagem) + 7(Apenas música) = 45
A probabilidade é igual ao que você "quer" dividido pelo "total". o que nós queremos são as pessoas que gostam de música, independente se gostam de mais outra forma de lazer, e esse valor corresponde a 45 e dividimos pelo total de servidores que é 75, chegando ao resultado.
45/75 = 0,60
Uma reportagem sobre “Comportamento no Trânsito” foi feita por um jornal de grande veiculação em uma determinada cidade brasileira. Nessa reportagem, foi feito um teste com 120 pessoas para entender como seriam suas reações diante de uma situação de risco no trânsito. O teste obteve os seguintes resultados:
– 60% das pessoas responderam que, quando o celular toca, logo atendem;
– 50% das pessoas responderam que nunca dirigem após a ingestão de bebida alcoólica; e
– 30% das pessoas responderam que atendem ao celular e nunca dirigem após ingerirem bebida alcoólica.
A partir desses dados, é correto afirmar que
GABARITO: A
30% é nossa interseção
50% - 30% achamos o valor dos que apenas NUNC... = 20%
60% - 30% achamos o valor dos que apenas ATEND... = 30%
Basta resolver a
120 . 30/100 >> 12 . 30/10 >> 12 . 3 = 36
(Dica se houver 0 no "capital" não divide a % por 100 logo de cara corta os zeros primeiro.)
120 . 20/100 >> 12 . 20/10 >> 12 . 2 = 24
Ficando assim:
24 pessoas que apenas... nunca ingerem...
36 pessoas que apenas... atendem celular
36 pessoas que fazem os 2
Totalizando 96 pessoas que responderam a entrevista, 24 se abstiveram.
a) 96 pessoas atendem ao celular ou não ingerem bebida alcoólica se forem dirigir.
Por exclusão das alternativas da pra responder, contudo vou explicar a razão da letra A, basta olhar a tabela verdade do conectivo ou (v) ou seja só é falso quando nenhuma das afirmações é verdadeira, ou seja,
P v Q
V F (quando apenas as pessoas que atendem) 36
F V (quando apenas as pessoas que nunca..) 24
V V (quando apenas as pessoas que fazem os 2) 36
F F preposição falsa.
A soma de todos as preposições verdadeiras é 96.
Considere que uma pesquisa de mercado tenha sido realizada na cidade de Parintins. Após o resultado, verificou- se que 1.000 pessoas usavam dois tipos de cremes dentais branqueadores, denominados E ou F; que o creme dental F é usado por 400 pessoas; e que 160 usam os dois cremes.
Assinale a opção que apresenta o número de pessoas que usam apenas o creme dental E.
b-
total = 1000
ambos = 160
F = 400. SOMENTE F: 400 - 160 = 240.
SOMENTE E: 1000 - (240+160) = 600
b-
total = 1000
ambos = 160
F = 400. SOMENTE F: 400 - 160 = 240.
SOMENTE E: 1000 - (240+160) = 600
Num grupo de 80 pessoas, 65% jogam basquete e 75% jogam vôlei. Desse grupo, a porcentagem de pessoas que praticam apenas vôlei é de:
Fiz do mesmo modo que a Ludiana Bandeira
Eu também utilizei a teoria dos conjuntos, mas como a questão não disse que todos praticam esportes, fiz da seguinte forma:
x = quem não pratica esportes
Quem não pratica vôlei: 100 - 75 = 25%
Quem não pratica basquete: 100 - 65 = 35%
Assim temos:
Quem pratica apenas vôlei: 35 - x
Quem pratica apenas basquete: 25 - x
Quem pratica as duas modalidades: 40 - x
Então somando tudo temos:
35 - x + 25 - x + 40 - x + x = 100%
100 - 2x = 100
x = vazio
Por isso que quem desconsiderou as pessoas que não praticavam esportes também acertou a questão.
Resposta: 35%
65% -> basquete
75%-> volei
1o passo) Regra de três para descobrir quantos jogam basquete
80 - 100
x - 65
5200 = 100, logo x = 52
2o passo) Regra de três para descobrir quantos jogam volei
80 - 100
75 - x
6000 = 100x, logo x = 60
3o passo) Se o grupo possui somente 80 pessoas, é preciso somar o número de pessoas que jogam volei e basquete subtrair o número de pessoas do grupo para verificar quantas estão em mais de um grupo.
Assim, 60+52= 112 e 112-80 = 32
4o passo) Como a questão pede o percentual de pessoas do grupo que jogam apenas volei, vamos substrair do numero total que joga volei o número de pessoas que joga os dois esportes e depois fazer uma regra de três para transformar em uma porcentagem.
60 - 32 = 28
28 - x
80 - 100
2800 = 80x
35 = x
Questão mal elaborada!
Deveria ser ANULADA, pois existem várias combinações possíveis para as informações apresentadas.
Pois, conforme o Joao Mischiatti afirmou, faltou a informação de que todas as pessoas praticam pelo menos um esporte.
Quem achou direto a resposta, não observou a falha da banca.
(fora a falha, questão fácil toda vida)
Questao legal, gostei
Bom, resolvi dessa maneira!
65% + 75%: 140%
140% -100%: 40
75%-40%: 35%
60 - 32 = 28
28 - x
80 - 100
2800 = 80x
35 = x
A.
simples, dos 140% que é o total, entende-se que 40% joga os dois, então se quer saber só vôlei, 75% - 40% = 35%
Uma entrevista foi realizada com um grupo de 200 pessoas sobre o uso de medicamentos para emagrecer, a prática de atividades físicas e de regime alimentar. Verificou-se que 43 pessoas não realizam nenhuma das três medidas e 22 pessoas realizam as três; 87 pessoas praticam regime alimentar, 75 pessoas usam medicamentos para emagrecer; 89 pessoas praticam atividades físicas; 37 pessoas praticam regime alimentar e atividades físicas; 40 pessoas praticam regime alimentar e usam medicamentos para emagrecer; 39 praticam atividades físicas e usam medicamentos para emagrecer. Quantas pessoas realizam pelo menos duas das medidas citadas?
Regime Alimentar 87
Medicamentos para emagrecer 75
Atividade Física 89
Sabes que 22 pessoas praticam estas três coisas então vais ter de subtrair este numero ao numero de pessoas que pratica apenas 2 das coisas, sendo assim
40-22=18, ou seja 18 pessoas praticam regime alimentar e medicamentos para emagrecer
39-22=17, ou seja 17 pessoas praticam atividade físicas e usam medicamentos
37-22=15, ou seja 15 pessoas praticam regime alimentar e atividades físicas
Agora que já encontr os valores das pessoas que praticam apenas duas das coisas vais ter de subtrair aos valores que sobram as pessoas que praticam 2 ou mais coisas,
87-15-18-22=32, ou seja, 32 pessoas praticam apenas regime alimentar
75-18-22-17=18, ou seja 18 pessoas usam apenas medicamentos
89-15-22-17=35, ou seja 35 pessoas apenas praticam atividade física
Recordando que queres saber quantas pessoas praticam pelo menos duas medidas então agora basta somar. Se no enunciado diz "pelo menos" então quer dizer que pode ser 2 ou mais, então vem que:
18+22+15+17=72
Num grupo de 250 pessoas, 34 usam óculos e lente de contato, 29 usam apenas lente de contato e 95 não usam nem óculos nem lente de contato. Quantas pessoas desse grupo usam apenas óculos?
Somei todos os valores ( 34+ 29+95 = 158), depois subtraí 158 de 250 = 92
Primeiramente vamos tirar os que não usam nenhum dos 2 que são 95 pessoas.
Então 250 - 95 = 155
Agora vamos somar os outros dois grupos que são as pessoas que usam lente e mais as que usam oculos e lente 34+ 29 = 63
Agora é só subtrair 155 - 63 = 92
Gabarito: C
Sendo M = { x ∈ R / -1 ≤ x < 3 }, N = { x ∈ R / x > 1 } e Q = ] -∞ , 2] pode-se afirmar que
Hoje não existe mais cumprir inicialmente em regime fechado!
Deve-se analisar as circunstâncias que envolvem o crime.
Thiago, depende do ponto de vista, se pedir com base na lei de crime hediondo deve-se ir pela literalidade da lei. Se pedir com base em jurisprudência do STF ai é outra historia.
Fique atento e leia letra de lei!
Sendo M = {2,3,7,8,9}; C o conjunto formado pelos elementos de M que são números primos; D o conjunto formado pelos elementos de M que são quadrados perfeitos; e E = { x ∈ M/x-1 ≥ 2}, é correto afirmar que
M={2,3,7,8,9}
C={2,3,7}
D={9}
E={3,7,8,9}
Considere que tenha sido realizada uma pesquisa no Amazonas Shopping sobre o que as pessoas compravam para presentear no Dia dos Pais. O resultado dessa pesquisa foi o seguinte:
– 75% dos entrevistados optaram por calçados;
– 60% dos entrevistados optaram por perfumes;
– 35% dos entrevistados optaram por perfumes e calçados.
Assinale a opção que apresenta a porcentagem dos entrevistados que compraria apenas perfumes.
60 - 35 = 25 - LETRA C
acertei, mas tenho a ligeira impressão que não pelos motivos certos
O item abaixo apresenta dados hipotéticos a respeito de uma pesquisa, também hipotética, seguidos de uma assertiva a ser julgada.
Uma pesquisa foi feita entre estudantes, para identificar quem fala inglês ou espanhol. Entre os pesquisados, 100 alunos responderam que falam inglês; 70 responderam que falam espanhol; 30 responderam que falam inglês e espanhol e 45 responderam que não falam nenhuma dessas duas línguas. Nessa situação, é correto afirmar que o número total de estudantes pesquisados foi de 185.
Resolvi a questão fazendo o DIAGRAMA:
30 - falam ambas as línguas
Inglês ----- 100-30= 70
Espanhol ----- 70-30 = 40
Logo ---- 70+40+30(interlocução) = 140
Na questões diz que 45 falam nenhuma dessas línguas
Logo ---- 140+45 = 185
Acho que é isso.
X=100+70-30
X=140
140+45= 185
gabarito correto, resolução:
http://sketchtoy.com/69303644
30 é a intercessão, ok?
100 falam inglês 》100-30=70
70 falam espanhol 》70-30=40
100(total de pessoas que falam inglês) +40= 140+45=185
A intercessão eu somei junto com 100
Gab: certo
Resolvido:
https://youtu.be/Rj6Jizx6RZM
Dos 36 funcionários de uma Agência do Banco do Brasil, sabe-se que: apenas 7 são fumantes, 22 são do sexo masculino e 11 são mulheres que não fumam. Com base nessas afirmações, é correto afirmar que o
| | FUMANTES | NÃO-FUMANTES | TOTAL |
| Mulheres | 03 | 11 | 14 |
| Homens | 04 | 18 (Resposta) | 22 |
| Total | 07 | 29 | 36 |
36 - 7 = 29 funcionários não fumam
29 - 11 (mulheres não fumam) = 18 homens não fumam
Total de funcionários HOMENS = 22
22 - 18 (não fumam) = 4 fumam
36 (funcionários) - 22 (funcionários homens) = 14 funcionárias mulheres
Total de funcionárias MULHERES = 14
14 - 11 (não fumam) = 3 fumam
a) número de homens que não fumam é 18.
b) número de homens fumantes é 5 - ERRADO.
c) número de mulheres fumantes é 4 - ERRADO.
d) total de funcionários do sexo feminino é 15 - ERRADO.
e) total de funcionários não fumantes é 28 - ERRADO. 18 (homens não fumantes) + 11 (mulheres não fumantes) = 29
Como o total de funcionários é 36, tem-se:
→ 7 são fumantes, logo 29 são não fumantes;
→ 22 são do sexo masculino, logo 14 são do sexo feminino;
→ 11 são mulheres que não fumam, logo 3 são mulheres que fumam.
Se 7 são fumantes e desses 3 são mulheres, então 4 homens são fumantes;
Se 22 são homens e desses 4 são fumantes, então 18 homens não são fumantes.
(Resposta A)
só uma dica: fazer por círculos fica mais fácil.
Total de funcionários = 36
são fumantes = 7
sexo masculino = 22
sexo feminino = 36 - 22 = 14
mulheres que não fumam = 11
mulheres que fumam = 14 - 11 = 3
Lembrando que 7 são fumantes, agora é só subtrair do número de mulheres que fumam que encontraremos o total de homens que fumam.
total de fumantes - nº de mulheres que fumam = nº de homens que fumam ------>>>> 7 - 3 = 4
homens que fumam = 4
homens que não fumam = 22 - 4 = 18
TOTAL DE FUNCIONÁRIOS NÃO FUMANTES = 11 + 18 = 29
A) CORRETO
B) ERRADO - número de homens fumantes é 4.
C) ERRADO - número de mulheres fumantes é 3.
D) ERRADO - total de funcionários do sexo feminino é 14.
E) ERRADO - total de funcionários não fumantes é 29.
fiz um diagrama de Venn, é bem mais fácil.
Solução em vídeo:
https://youtu.be/mlZ9cu_Tj-Q
22 são do sexo masculino
11 são mulheres que não fumam
apenas 7 são fumantes
total de 36 funcionários
22+7 = 29
11+7 = 18
29-36 = 7
11-36 = 25
25-7 = 18
Então número de homens que não fumam é 18.
Resposta certa é LETRA (A)
gabarito estranho. O complemento de um conjunto sao todos os elementos que nao sao parte dele. Se unir um complemento com seu conjunto, o resultado sera todos os elementos possiveis dentro de um universo U, o que valida a 'a' como resposta correta.
Seria como nessa imagem abaixo, mas N seria X, Z seria U e Q seria Y
https://www.infoescola.com/wp-content/uploads/2007/07/conjunto-racionais.jpg
Gloomy gulch, Y nao é complemento de X, Y é complemento do complemento de X, ou seja, o proprio X.
LEP:
Art. 52. A prática de fato previsto como crime doloso constitui falta grave e, quando ocasionar subversão da ordem ou disciplina internas, sujeitará o preso provisório, ou condenado, nacional ou estrangeiro, sem prejuízo da sanção penal, ao regime disciplinar diferenciado, com as seguintes características: (Redação dada pela Lei nº 13.964, de 2019)
I - duração máxima de até 2 (dois) anos, sem prejuízo de repetição da sanção por nova falta grave de mesma espécie; (Redação dada pela Lei nº 13.964, de 2019)
II - recolhimento em cela individual; (Redação dada pela Lei nº 13.964, de 2019)
III - visitas quinzenais, de 2 (duas) pessoas por vez, a serem realizadas em instalações equipadas para impedir o contato físico e a passagem de objetos, por pessoa da família ou, no caso de terceiro, autorizado judicialmente, com duração de 2 (duas) horas; (Redação dada pela Lei nº 13.964, de 2019)
IV - direito do preso à saída da cela por 2 (duas) horas diárias para banho de sol, em grupos de até 4 (quatro) presos, desde que não haja contato com presos do mesmo grupo criminoso; (Redação dada pela Lei nº 13.964, de 2019)
V - entrevistas sempre monitoradas, exceto aquelas com seu defensor, em instalações equipadas para impedir o contato físico e a passagem de objetos, salvo expressa autorização judicial em contrário; (Incluído pela Lei nº 13.964, de 2019)
VI - fiscalização do conteúdo da correspondência; (Incluído pela Lei nº 13.964, de 2019)
VII - participação em audiências judiciais preferencialmente por videoconferência, garantindo-se a participação do defensor no mesmo ambiente do preso. (Incluído pela Lei nº 13.964, de 2019)
LEP:
Art. 52. A prática de fato previsto como crime doloso constitui falta grave e, quando ocasionar subversão da ordem ou disciplina internas, sujeitará o preso provisório, ou condenado, nacional ou estrangeiro, sem prejuízo da sanção penal, ao regime disciplinar diferenciado, com as seguintes características:
§ 1º O regime disciplinar diferenciado também será aplicado aos presos provisórios ou condenados, nacionais ou estrangeiros:
I - que apresentem alto risco para a ordem e a segurança do estabelecimento penal ou da sociedade;
II - sob os quais recaiam fundadas suspeitas de envolvimento ou participação, a qualquer título, em organização criminosa, associação criminosa ou milícia privada, independentemente da prática de falta grave.
§ 2º (Revogado).
§ 3º Existindo indícios de que o preso exerce liderança em organização criminosa, associação criminosa ou milícia privada, ou que tenha atuação criminosa em 2 (dois) ou mais Estados da Federação, o regime disciplinar diferenciado será obrigatoriamente cumprido em estabelecimento prisional federal.
§ 4º Na hipótese dos parágrafos anteriores, o regime disciplinar diferenciado poderá ser prorrogado sucessivamente, por períodos de 1 (um) ano, existindo indícios de que o preso:
I - continua apresentando alto risco para a ordem e a segurança do estabelecimento penal de origem ou da sociedade;
II - mantém os vínculos com organização criminosa, associação criminosa ou milícia privada, considerados também o perfil criminal e a função desempenhada por ele no grupo criminoso, a operação duradoura do grupo, a superveniência de novos processos criminais e os resultados do tratamento penitenciário.
Dica: Quando o exercício (independente do assunto) não descriminar quais são os elementos envolvidos (neste caso são os elementos conjuntos que não foram explícitos) você pode supô-los.
Solução: Como ele não descriminou os elementos, podemos supor que U = {1,2,3,4,5}. X = subconjunto não vazio de U; vamos supor que X = {1,2}
Ele diz que: "Y é complemento do complemento de X em relação a U", vamos por partes, de trás pra frente:
2ª parte: "complemento de X em relação a U" vamos chamar de C1, que será: C1 = U - X = {3,4,5}
1ª parte: agora a primeira parte: "Y é complemento de C1 em relação à U", portanto: Y = U - C1 = {1,2}
Chegamos à seguinte conclusão: X = {1,2} e Y = {1,2}. Analisando as alternativas chegamos à alternativa E: X ∩ Y = X; como os conjuntos são idênticos, de fato, a interseção deles é igual a ambos os conjuntos.
Gab.: E ✓
A questão afirma que Y é o complemento do complemento de X. Ora, o complemento do complemento de um conjunto é o próprio conjunto. Portanto, X e Y são o mesmo conjunto!
A interseção entre X e Y será o próprio conjunto X.
Obs: se a questão afirmasse que a interseção entre X e Y é igual a Y, também estaria correta, pois X e Y são o mesmo conjunto!
Saber correlacionar conjuntos e lógica proposicional ajuda em questões desse tipo.
O conjunto complementar corresponde à negação na lógica de proposições. Dessa forma:
Y = ~(~X)
Y = X
Dados fornecidos pelo item:
• Conjunto U, do qual X é um subconjunto não vazio e próprio;
• Seja Y o complemento do complemento de X (os complementos sendo considerados em relação a U).
Perceba que o examinador está querendo que o candidato descubra qual das alternativas descritas condiz com os dados fornecidos pelo enunciado. Como fica difícil visualizar o item dessa maneira, iremos utilizar exemplos numéricos para facilitar a visualização da questão. Note:
O examinador afirma que temos o conjunto U, do qual X é um subconjunto não vazio e próprio, logo:
U = {1, 2, 3}
X = {1, 2}
Veja que os números supracitados foram escolhidos de forma aleatória, o candidato poderia ter escolhido outros números a fim de resolver a questão.
Logo depois, a banca afirma que Y é o complemento do complemento de X (os complementos sendo considerados em relação a U). Como o conjunto X um subconjunto do conjunto U, podemos inferir que Y é o complemento de U que é complemento de X. Assim, visualizando de maneira numérica, teríamos:
Y = {1, 2, 3, 4}
U = {1, 2, 3}
X = {1, 2}
Dessa maneira, a intercessão de X e Y é igual ao próprio X, que corresponde à parte sombreada acima.
Resposta: E
Mil pessoas responderam a uma pesquisa sobre a frequência do uso de automóvel. Oitocentas e dez pessoas disseram utilizar automóvel em dias de semana, 880 afirmaram que utilizam automóvel nos finais de semana e 90 disseram que não utilizam automóveis. Do total de entrevistados, quantas pessoas afirmaram que utilizam automóvel durante a semana e, também, nos fins de semana?
Analisando os dados oferecido no enunciado, montaremos a seguinte equação abaixo:
810 + 880 + 90 - = 1000 → x = 1780 – 1000 → x = 780 utilizam automóvel durante a semana e, também, nos fins de semana.
Letra E.
1000 - 90 = 910 (Pessoas que usam automóvel)
910 - 810 = 100 (Pessoas que só usam no fds)
910 - 880 = 30 (Pessoas que só usam durante a semana)
100 + 30 = 130
910 - 130 = 780
Questão de conjuntos. Onde a resposta está na intercessão entre usuários do meio de semana e usuários de fins de semana.
Dados fornecidos pelo item:
• Mil pessoas responderam a uma pesquisa sobre a frequência do uso de automóvel;
• Oitocentas e dez pessoas disseram utilizar automóvel em dias de semana;
• 880 afirmaram que utilizam automóvel nos finais de semana;
• 90 disseram que não utilizam automóveis.
A banca quer saber quantas pessoas afirmaram que utilizam automóvel durante a semana e, também, nos fins de semana, ou seja, a interseção entre os conjuntos. Assim, segue a análise:
• 90 disseram que não utilizam automóveis, ou seja, essas 90 pessoas não participam de nenhum dos dois conjuntos;
• Chamaremos de X a interseção entre ambos os conjuntos, assim temos que:
• Pessoas que utilizam automóvel somente em dias de semana = 810 – X
• Pessoas que utilizam automóveis somente nos finais de semana = 880 – X
• Assim, para calcular o valor de X, que representa quantas pessoas afirmaram que utilizam automóvel durante a semana e, também, nos fins de semana, basta fazer o seguinte cálculo:
810 – X + X + 880 – X + 90 = 1000
810 + 880 – X +90 = 1000
1780 – X = 1000
– X = 1000 – 1780
– X = - 780
X = 780
A seguir encontra-se a representação em forma de conjuntos:
Resposta: E
Total : 1.000
Dias de semana: 810
Finais de semana: 880
Nenhum: 90
Soma: 810+880+90= 1780
1780-1000= 780 dias de semana e fins de semana
1000-90 = 910
910 - 810 = 100
910 - 880 = 30
100 + 30 = 130
910 - 130 = 780
Sejam S o conjunto de busca, N a relação de vizinhança e g a função avaliação. De um pseudoalgoritmo de busca local estocástica retiram-se os seguintes comandos:
determine N(s) = {s’ ∈ S | (s, s’) ∈ N};
determine I*(s) = {s’ ∈ N(s) | g(s’) = g*}, onde g* = min{g(s’) | s’ ∈ N(s)};
s’:= escolha aleatória segundo uma distribuição uniforme em I*(s) não
vazio.
Uma alternativa para aumentar a rapidez dos algoritmos de busca local estocástica é selecionar o próximo passo de maneira mais eficiente. Neste contexto, o mecanismo de seleção do passo de busca do algoritmo, cujos comandos foram destacados acima, usa a estratégia de seleção
como resolve essa ??
Se A = { 1,2}; B={{2},{1,2}} e C={1,2,{2},{1,2},{{2},{1,2}}}, então:
Se eu não ? Então eu não ?
Não entendi. Não sei como resolver essa questão. Alguém????
É provável que o site não aceite os sinais de pertence e contém. Vamos lá, as alternativas corretas são:
a) A contém B
b) A interseção B = {1,2}
c) A - B = vazio
d) C - (A - B) contém B
e) (A interseção C) pertence à B
Possível explicação para a questão:
Alternativa A: ERRADA
A não está contida em B. O termo {1,2} em B é diferente dos termos 1,2 em A
Alternativa B: ERRADA
A interseção de B é vazio, pois não existem termos iguais em tais conjuntos.
Alternativa C: ERRADA
A-B = {1,2}
Alternativa D: ERRADA
A-B = 1,2
C - 1,2 = {{2},{1,2},{{2},{1,2}}}
{{2},{1,2},{{2},{1,2}}} não contém B (é visível também por B ter menos termos no conjunto)
Alternativa E: CORRETA
A interseção de B é vazio, porém como todo conjunto possui um subconjunto vazio, pode-se dizer que essa alternativa está correta.
Achei a questão bem estranha, nível hard mesmo. Válido lembrar que esse certame teve diversas questões anuladas ou com gabarito alterado:
cargo: prof de matemática
eu pularia se fosse qualquer cargo, imagina pra professor de matemática.
(A^C) pertence a B
A^C= {1,2}
Esse conjunto é um elemento que pertence a B
Vcs estão confundindo elemento com subconjunto
Um professor de matemática dá aula particular para uma classe de 9 alunos, dos quais pelo menos um é brasileiro. Se o professor escolher 4 alunos para fazer uma apresentação, terá no grupo pelo menos dois alunos de mesma nacionalidade; se escolher 5 alunos, terá no máximo três alunos de mesma nacionalidade. Quantos brasileiros existem na classe?
Essa é uma questão que envolve o Princípio da Casa dos Pombos, com 2 condições:
i) Grupos de 4 com pelo menos 2 de mesma nacionalidade e
ii) grupos de 5 com no máximo 3 de mesma nacionalidade.
a) 1 - viola a condição i), pois posso compor um grupo que tem 1 pessoa com nacionalidade diferente
d) 4 e e) 5 - violam a condição ii)
b) 2 - Fixando um grupo com 2 nacionalidades no mínimo, teremos necessariamente AABBCCDDD, isto é, 3 grupos de 2 pessoas e 1 de 3. Mas então é possível escolher um grupo de 4 pessoas de nacionalidades diferentes (ABCD).
c) 3 - Se tem 3 brasileiros (B), tem duas possibilidades: BBBAACCDD, que não pode pela justificativa acima ou BBBAAACCC. Logo, temos 3 nacionalidades com 3 pessoas de cada.
Boa noite fera!
Essa questão é pura dedução.
Vamos lá, seguindo as informações: Sabemos que em total existe 9 alunos.
A) se formando um grupo de 4 pessoas resultará em pelo menos 2 pessoas de uma mesmo nacionalidade, então posso deduzir a impossibilidade de existir 4 nacionalidades. No caso obrigatoriamente terei 3 ou 2 nacionalidades. --> segue para o próximo passo. * Brasileiro, Americano, Mexicano ou Brasileiro e Americano*
B) Aqui é aonde você deduz a imposibilidade de ter somente 2 nacionalidades, por constar que o máximo de números de 1 nacionalidade é de 3 pessoas, portanto se você só tiver *Brasileiros e Americanos = somente haverá 6 pessoas, restando 3*
Conculsão: Você tem 3 nacionalidades com 3 pessoas cada.
Siga os passos para deduzir e resolver a questão, espero que ajuda amigo! Um forte abraço.
letra D
Suponha que haja alunos de 4 ou mais nacionalidades entre os 9 alunos da classe. Se escolhermos um aluno de cada nacionalidade não haverá dois alunos de mesma nacionalidade, o que é um absurdo. Logo há alunos de no máximo 3 nacionalidades.
Da mesma forma, entre os 9 alunos não há 4 de mesma nacionalidade, pois se houvesse poderíamos formar um grupo de 5 alunos com mais de 3 alunos de mesma nacionalidade. Logo há no máximo 3 alunos de cada nacionalidade.
Como há 9 alunos, no máximo 3 nacionalidades e no máximo 3 alunos por nacionalidade, há exatamente 3 nacionalidades e 3 alunos de cada nacionalidade. Em particular, há 3 alunos brasileiros. disponível em
https://anapaulamorgado.files.wordpress.com/2009/05/apostila_8c2ba_9c2ba2.doc
Eu errei, mas, depois, voltei atrás e tentei resolver usando a seguinte lógica.
Teria um grupo de 4, com dois de mesma nacionalidade e mais 2 de outras nacionalidades distintas.
Teria um grupo de cinco, sendo 3 pessoas com a mesma nacionalidade e mais 2 com nacionalidades diferentes.
Ou seja, o número de brasileiros está em meio a esses quatro de nacionalidades diferentes. Quando o autor falar em pelo menos, sempre é possível achar o resultado diminuindo o valor geral por -1.
4 - 1 = 3
ERREI PRIMEIRO, PORÉM ENTENDI A LÓGICA:
A QUESTÃO INFORMA O SEGUINTE: QUE DE 9 ALUNOS PELO MENOS 1 É BRASILEIRO.
DEPOIS DE ANALISAR A ÚLTIMA LINHA DO ENUNCIADO PERCEBI QUE ELE AFIRMA QUE NO GRUPO DE 5 TERÁ NO MAXIMO 3 ALUNOS DA MESMA NACIONALIDADE.
NA LÓGICA DE 1º ORDEM O PELO MENOS PODE SER COMPARADO COM O TODO E SE NEGAR ELE PODE SER TROCADO PELO ALGUM OU ALGUNS NO PLURAL
EU DEDUZIR QUE SE ELE AFIRMA QUE TEM 3 ALUNOS DE UMA MESMA NACIONALIDADE, ENTÃO PODERIA AFIRMAR QUE:
3 PODERIA SER ALEMÃO
3 PODERIA SER ARGENTINO
3 PODERIA SER BRASILEIRO ( 'PELO MENOS UM" NÃO DEIXA CLARO NA ESTRUTURA LÓGICA QUE EXISTE SÓ 1, SÓ LEMBRANDO A GALERA.)
Numa escola, os alunos têm a possibilidade de aprenderem até duas línguas estrangeiras, se assim desejarem. Entretanto 160 alunos da escola, de uma totalidade 300, optaram por não estudar qualquer uma das línguas estrangeiras oferecidas. Sabendo que 120 alunos estudam Inglês e 80 alunos estudam espanhol, a quantidade de alunos que estuda ambas línguas é
Nenhuma - 160
Inglês- 120
Espanhol - 80
360
O total de alunos é 300, o resultado é maior porque alguns estudam tanto inglês como espanhol. 60 é o número que superou a totalidade, esses são os que estudam ambas línguas.
e) 60.
Numa escola, os alunos têm a possibilidade de aprenderem até duas línguas estrangeiras, se assim desejarem. Entretanto 160 alunos da escola, de uma totalidade 300, optaram por não estudar qualquer uma das línguas estrangeiras oferecidas. Sabendo que 120 alunos estudam Inglês e 80 alunos estudam espanhol, a quantidade de alunos que estuda ambas línguas é


Total de alunos: 300
Não estudam: 160
Total de alunos - Não estudam = 300 – 160 = 140(total do alunos que fazem curso)
Inglês= 120
Espanhol=80
Inglês+Espanhol= 200
mas temos 140 pessoas então dessas 200 vamos tirar só os que fazem os 2 cursos
(Inglês+Espanhol) - (total do alunos que fazem curso)= 200- 140= 60
300 - 160 - 120 - 80 = - 60 (só transformar para positivo).
Na hora da prova tempo é tudo.
300-160= 140 (alunos que estudam alguma língua estrangeira)
120+80=200
200-140= 60 alunos que estudam ambas línguas.
Em um grupo de 25 pessoas, há 16 pessoas com mais de 25 anos e 17 com menos de 35 anos.
Nesse grupo, quantas pessoas têm mais que 25 e menos que 35 anos?
25 - 16 = 9 pessoas com menos de 25
25 - 17 = 8 pessoas com menos de 35
9 + 8 = 17
25 - 17 = 8 pessoas entre 25 e 35
Fórmula dos conjuntos:
AUB = A + B - A(interseção)B
25 = 16 + 17 - A(interseção)B
A(interseção)B = 33 - 25 = "8 pessoas maiores de 25 e menores de 35"
tb fiz isso...
tem logica ou foi sorte?
-----------
Rodrigo
17 de Fevereiro de 2012, às 21h03
Útil (9)
Bem... não ultilizei regras nem formulas...
foi assim
somei 16 com 17 que deu : 33 depois diminui pelo número total do grupo de pessoas 25 que deu 8.
valew. bons estudos ;)
Dados fornecidos pelo item:
• Em um grupo de 25 pessoas, há 16 pessoas com mais de 25 anos e 17 com menos de 35 anos;
A banca quer saber quantas pessoas têm mais que 25 anos e menos que 35 anos. Assim, observe a análise a seguir:
• Chamaremos de X a interseção entre ambos os conjuntos: pessoas com mais de 25 anos e pessoas com menos de 35 anos;
• Como chamamos de X a interseção entre ambos os conjuntos, temos que:
• pessoas somente com mais de 25 anos = 16 – X
• pessoas somente com menos de 35 anos = 17 – X
• Assim, para calcular o valor de X, que representa as pessoas que têm mais que 25 e menos que 35 anos, basta fazer o seguinte cálculo:
16 – X + X + 17 – X = 25
16 + 17 – X = 25
33 – X = 25
– X = 25 – 33
– X = - 8
X = 8
A seguir encontra-se a representação em forma de conjuntos:
Resposta: D
Total = 25 pessoas
+25 anos = 9 pessoas exatas ( 25-16)
-35 anos = 8 pessoas exatas ( 25-17)
25-17 ( que é a soma de 9+8) =
8 pessoas tem -35 anos e +25 anos
eu fiz o diagrama de veen e no lugar da intersecção que era os que tinham mais de 25 e menos de 35 eu coloquei x, nos que tinham mais de 25, que era 16 coloquei 16-x e nos que tinham menos que 35 usei 17-x, como a soma de todas as pessoas que participaram era 25 então ficou16-x+17-x+x=25 resolvendo se descobre o valor de x que é 8
25-16- 9 pessoas tem menos de 25 anos
25-17= 8 pessoas tem mais de 35 anos
quem tá entre 25 a 35 anos é justamente a quantidade de pessoas do grupo MENOS pessoas tem menos de 25 anos MENOS pessoas tem mais de 35 anos
25-9-8= 8
Em uma cidade, 1.000 habitantes foram entrevistados a
respeito de suas relações com os bancos A e B. Dos entrevistados,
450 eram correntistas apenas do banco A, 480 eram correntistas do
banco B, 720 eram correntistas de apenas um desses bancos e o
restante não era correntista de nenhum desses 2 bancos.
A respeito dessa pesquisa, é correto afirmar que a probabilidade de
um dos entrevistados
ser correntista dos 2 bancos é superior a 0,20.
Pelo diagrama apresentado no item 94, tem-se que a probabilidade de ser correntista dos dois bancos é:
P(dois bancos) = 210/1000 = 0,21
720 (correntistas apenas de um dos dois bancos)
450 (correntistas apenas do banco A)
720 - 450 = 270 (correntistas apenas do banco B)
480 (correntistas do banco B)
480 - 270 = 210 (correntistas dos dois bancos)
210/1000 = 0,21
Total de entrevistados: 1000
A A e B B
( 450 ) (x) ( 480 - x )
Sabemos que: 720 entrevistados podem ser A ou B, ele pode estar incluído ou no Conjunto A, ou no Conjunto B.
Então temos:
450 + 480 - x = 720
x=210 pessoas possuem conta nos dois bancos
A probabilidade de a pessoa ser dos dois bancos será: 210/1000 = 0,21
Certo.
Pensei assim:
1 > 1000 habitantes ;
2 > banco A e B:
3 > 450 apenas banco A; ( informação do próprio problema)
4 > 480 banco B; ( informação do próprio problema que nos faz entender que desses 480 com banco B também tem habitantes com Banco A, ou seja, banco A e B nesse meio)
5 > 720 apenas uma conta, ou seja, ou conta no banco A ou no Banco B; ( informação do próprio problema)
6 > Com o item 5 e o item 3, conseguimos chegar a conclusão de quantos habitantes possuem apenas a conta B:
- 720 (apenas uma conta) - 450 (apenas a conta A) = 270 ( apenas a conta B)
7 > Sabendo a quantidade de habitantes com apenas a conta B ( 270) e subtraindo do item 4, onde mostra a quantidade de habitantes com a conta B, teremos a quantidade de habitantes que possuem a conta A e B:
- 480 (habitantes que tem a conta B) - 270 (habitantes que tem apenas a conta B) = 210 ( habitantes com a conta A e B)
8 > Somando 450 + 270 + 210 teremos 930 habitantes que possuem conta no banco, logo, 1000 (habitantes) - 930 (habitantes com contas) = 70 ( habitantes sem conta em qualquer banco)
9 > Resumindo:
- Habitantes apenas a conta A : 450
- Habitantes apenas a conta B : 270
- Habitantes com a conta A e B : 210
- Habitantes sem conta em qq banco : 70
10 > O problema pede a porcetagem de habitantes com conta A e B:
- 1000 (habitantes) - 100%
210 (habitantes com conta no banco A e B) - x %
- x = 21 % que é igual a 0,21;
11 > Portanto, ser correntista de 2 bancos é superior a 0,20!
Jesus no comando, SEMPRE!!!
TOTAL; 1000 HB
A= 450..... + B= 480...... = 930
720 eram de A ou B
930-720= 210 ..... 210/1000= 0,21
questão de verdade! topada RUMO PMAL 2020
Resposta: CERTO.
Comentário do professor Joselias Silva no YouTube:
https://youtu.be/m2-LBOt8Rjc
Considere verdadeiras as afirmações:
I. Todo motorista é professor.
II. Existem atletas que são motoristas.
III. Nenhum atleta é jornalista.
IV. Alguns jornalistas são motoristas.
A simbolizando o conjunto dos atletas, J, o dos jornalistas, P, o dos professores e M, o dos motoristas, o diagrama que melhor representa as afirmações supracitadas é
Segundo o gabarito, a correta é a letra D.
Acredito que o correto seria a letra C.
O gráfico indicado na D não representa corretamente a afirmação II.
Graziela, a letra D se refere ao quarto gráfico, acho que está condizente com os enunciados!
Os gráficos estão certos, a posição que se encontra as alternativas é que pode levar a pessoa a marcar no local errado. Gabarito letra D
Acertei, marquei a letra D, mas quando fui selecionar escolhi a letra C sem perceber por causa da disposição dos diagramas.
Em uma turma de 100 alunos, 63 sabem escrever apenas com a mão direita, 5 não sabem escrever, 25% dos restantes sabem escrever tanto com a mão direita quanto com a esquerda, e os demais alunos sabem escrever apenas com a mão esquerda. Dessa turma, a porcentagem de alunos que sabe escrever com apenas uma das duas mãos é de
Amigos,
Cheguei ao resultado da seguinte forma:
Mão Direita (MD) : 63; Nenhuma das Mãos (NDM) : 5; Mão Esquerda (ME) : ? As duas mãos (AM) : (100 - MD + NDM) * 25%
1º Passo: Somando: MD + NDM temos:
63 + 5 = 68.
2º Passo: Descobrir os alunos restantes:
100 - 68 = 32.
3º Passo: Aplicar o percentual indicado (25%) p/ Descobrir Alunos Esquerdos e Canhotos ao mesmo tempo (AM):
AM == 32 * 25% = 8.
4º Passo: ME = 100 - MD + AM + NDM - Substituindo temos:
ME = 100 - 63 + 8 + 5
ME = 24.
5º Passo: Encontrar o percentual de quem escreve apenas com MD e apenas com ME:
(ME + MD)/100 == (24 + 63)/100 = 87/100 == 87%
Portanto, Letra B.
Espero ter ajudado.
Bons Estudos!!!
Não concordo que deva ser anulada a questão, ele realmente quer somente os alunos que escrevem com apenas uma mão, logo 24 alunos escrevem apenas com a esquerda e 63 alunos escrevem apenas com a direita, totalizando 87 alunos que escrevem apenas com uma das mãos.
Galera encontrei um jeito bem simples.
Número total de alunos: 100
Alunos que não sabem escrever: 5
logo ja tenho: 100 - 5= 95
25% dos restantes escrevem com as duas mãos: 8 (que foi encontrado usando a regra de três)
logo, 95-8= 87
convertendo para porcentagem: 87%
Espero ajudar!
100-5 (não sabem) = 95 ( sabem escrever)
95-63 (escrevem com a direita) = 32 (restante) * 25% = 8 (escrevem com as duas)
24 que restou escreve com a esquerda e 63 com a direita (63+24) = 87 total dos que escrevem ou com a direita, ou com a esquerda.
Para facilitar a interpretação :
63 = > Alunos que escrevem com apenas uma das mãos
5 = > Não sabem escrever
8 = > Escrevem com as duas mãos
24 = > Escrevem com apenas uma das mãos
63 + 24 = 87
--------------------------------------------------------------------------------------------------------------------------------------------------------------------Soma-se 63 + 5 para saber quantos alunos temos até ai = > 68 Alunos.
Agora fazemos um calculo para saber quantos são os 25 % que escrevem com as duas mãos = >
68 alunos - ( menos ) o total de alunos, que é 100 = 32 Alunos , agora fazemos 25% de 32 , que é igual á => 8 Alunos ( Esses 8 Alunos sabem escrever com as duas mãos, como diz o enunciado, pois eles são os 25% )
Assim temos , 63 Alunos + o restante dos 32 Alunos menos os 8 que representam os 25% que escrevem com as duas mãos, ( 32 - 8 = 24 )
Como 5 alunos não sabem escrever , fica assim.
63 Alunos + 24 Alunos = 87 Alunos que escrevem com apenas uma das mãos.
Como o total de alunos são 100, = 87% LETRA B
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
Na turma, 63 alunos sabem escrever apenas com a mão direita, 5 não sabem escrever, assim temos até aqui um total de 68 alunos.
25% dos restantes sabem escrever tanto com a mão direita quanto com a esquerda, ou seja:
100
– 68 = 32 (Alunos restantes), 25% desse valor é igual a 8 alunos, logo esse é o
número de alunos que sabem escrever tanto com a mão direita quanto com a
esquerda.
Assim, a quantidade de alunos que sabem escrever apenas com a mão esquerda é de 100 - (63 + 8 + 5) = 24, logo a quantidade de alunos que sabem escrever apenas com uma mão é de 63 + 24 = 87. Aplicando uma regra de três simples para se calcular a porcentagem de alunos que sabe escrever com apenas uma das duas mãos:
100 alunos ---- 100%
87 alunos ---- X%
100.X = 87.100
Leonardo Caldas! Não divague na questão...
Leia o enunciado novamente e entenda que 25% é correspondente ao restante que sabe escrever e não para a totalidade dos alunos, isto é:
100 alunos - 63 alunos (Mão Direita) - 5 alunos (Ñ escrevem) = 32 alunos.
25% de 32 = 8 alunos (Mão Esquerda e Mão Direita).
100 alunos - 8 alunos ambidestros - 5 alunos que não escrevem = 87 alunos que escrevem apenas com uma das mãos (ou esquerda ou direita)
Ou seja, 87 de 100 = 87%
100 alunos, onde:
63 são destros
5 não sabem escrever
Sobram 32 ( 25% são ambidestros - 8 alunos e 75% são canhotos - 24 alunos)
Os que escrevem com uma das mãos: destros (63) + canhotos (24) = 87.
8 escrevem com as duas 5 não sabem escrever, logo 13 escrevem com as duas mãos ou não sabem escrever, assim 100 (todos)- 13( os que não escrevem ou escrevem com as duas)= 87. MUITO MAIS SIMPLES !
100-63=37
37-5=32
25% de 32=8
24 - mão esquerda
63(md)+24(me)=87
Subtraindo do total (100 alunos) aqueles que só usam a mão direita (63) e os que não sabem escrever (5), ficamos com:
Restante = 100 – 63 – 5 = 32 alunos
Foi dito que 25% do restante (32 alunos) escrevem com ambas as mãos, ou seja:
Escrevem com ambas = 25% de 32
Escrevem com ambas = 25% x 32
Escrevem com ambas = 0,25 x 32
Escrevem com ambas = 8 alunos
Assim, os demais alunos escrevem apenas com a esquerda:
Escrevem só com a esquerda = 32 – 8
Escrevem só com a esquerda = 24 alunos
destros, totalizando:\
Escrevem só com uma mão = 24 + 63
Escrevem só com uma mão = 87 alunos.
Como 87 dos 100 alunos escrevem só com uma mão, eles correspondem a 87% do total.Resposta: B
Comentários:
Dados:
(T) Total da Turma: 100 alunos
(I) Alunos que escrevem com a mão DIREITA: 63 alunos
(II) Alunos que NÃO SABEM ESCREVER: 5 alunos
(III) 25% do restante, ou seja, de (T) – (I + II), logo (III) será:
100 – (63+5)>>100 – 68 = 32*0,25 (25%) = 8 alunos
(IV) Alunos que escrevem com a mão ESQUERDA: SERÁ (T) – (I + II + III), ou seja, 100 – (63+5+8)>>100-76 = 24 alunos
Por fim: a questão quer saber quantos escrevem com apenas uma das mãos, ou seja, (I) + (IV)>>63+24=87 alunos. Agora basta uma regra de três simples para matar a questão:
100-----100%
87-------X%
X=87%
Gabarito: B
TOTAL DE ALUNOS = 100
APENAS COM A MÃO DIREITA = 63
NÃO SABEM ESCREVER = 5
25% DO RESTANTE(100 - 63 - 5 = 32) SABEM ESCREVER TANTO COM A MÃO DIREITA QUANTO COM A ESQUERDA(INTERSECÇÃO) = 25% x 32 = 8
SOMENTE COM A ESQUERDA = 100 - 63 - 5 - 8 = 24
SOMENTE COM A MÃO DIREITA = 63
INTERSECÇÃO = 8
NÃO SABEM ESCREVER = 5
24 + 63 + 8 + 5 = 100
PORCENTAGEM QUE SABE ESCREVER COM COM APENAS UMA DAS MÃOS = 24 + 63 = 87%
100......100%
87.........X
X = 87%
GABARITO B
RESOLUÇÃO:
Subtraindo do total (100 alunos) aqueles que só usam a mão direita (63) e os
que não sabem escrever (5), ficamos com:
Restante = 100 – 63 – 5 = 32 alunos
Foi dito que 25% do restante (32 alunos) escrevem com ambas as mãos, ou
seja:
Escrevem com ambas = 25% de 32
Escrevem com ambas = 25% x 32
Escrevem com ambas = 0,25 x 32
Escrevem com ambas = 8 alunos
Assim, os demais alunos escrevem apenas com a esquerda:
Escrevem só com a esquerda = 32 – 8
Escrevem só com a esquerda = 24 alunos
Os alunos que escrevem com apenas 1 mão são os 24 canhotos e os 63
destros, totalizando:
Escrevem só com uma mão = 24 + 63
Escrevem só com uma mão = 87 alunos
Como 87 dos 100 alunos escrevem só com uma mão, eles correspondem a
87% do total.
Resposta: B
Até que fim acertei uma
Até que enfim...Ufa!! Quem foi o demônio que criou esta matéria? Não respondem para eu não tomar ódio!!
Minha gente, que questões são essas? Tô perdida!
#MalditaFCC
usem diagramas de venn que fica facil.
Saudade de quando existiam figuras nos comentários; Daí dava para ver os Diagramas de Venn certinho;
MAO DIREITA = 63
MAO ESQUEDA = 24
RESPOSTA=87
Explicação em vídeo: https://www.youtube.com/watch?v=s4BZl3fujY0
63 + 24 = 87
Julgue o item a seguir, acerca de raciocínio lógico.
Considere que em um canil estejam abrigados 48 cães, dos quais:
• 24 são pretos;
• 12 têm rabos curtos;
• 30 têm pêlos longos;
• 4 são pretos, têm rabos curtos e não têm pêlos longos;
• 4 têm rabos curtos e pêlos longos e não são pretos;
• 2 são pretos, têm rabos curtos e pêlos longos.
Então, nesse canil, o número de cães abrigados que são pretos, têm pêlos longos mas não têm rabos curtos é superior a 3 e inferior a 8.
Temos 3 conjuntos: cães pretos, com rabos curtos e com pelos longos.
Começando pela intersecção, colocaremos 2 (cães pretos, com rabos curtos e pêlos longos) entre os 3 conjuntos. Depois:
- 4 são pretos, têm rabos curtos e não têm pêlos longos => coloquem 4 na intersecção de pretos e rabos curtos;
- 4 têm rabos curtos e pêlos longos e não são pretos => coloquem 4 entre rabos curtos e pelos longos;
Agora:
- 24 são pretos => fica ‘24 – 4 – 2 – x’ = 18 – x
- 12 têm rabos curtos => fica ‘12 – 4 – 4 – 2’ = 2
- 30 têm pêlos longos => fica ‘30 – 4 – 2 – x’ = 24 – x
Agora, só precisamos somar todos os elementos e igualarmos a 48 (total de cães):
(18 – x) + 2 + (24 – x) + 4 + 4 + x + 2 = 48
-x + 54 = 48
x = 6 (portanto, superior a 3 e inferior a 8).
Item correto
Por que que não pode os 18 cães pretos que sobraram serem todos de pelos longos ? Ainda sobraria 6 que teriam somente pelos longos...
Eu entendi o que o colega Dieggo Oliveira fez mas eu não entendi porque a resolução tem que ser dessa maneira. Alguém pode explicar melhor?
Serenna Alves, acredito que seja uma das maneiras de resolver. Vi num livro de questões da CESPE, que essa questão era resolvida por árvore binária. Mas não entendi nada...rs
Com a explicação do Dieggo, eu consegui entender melhor. Só faço uma consideração a mais na explicação dele:
-Na hora de somar todos os grupos (preto + rabo curto + pelo longo), cujo total é 48, não é possível somar: 24 + 12 + 30 (que daria 66), porque há intersecções, ou seja, tem números que se repetem (faça três círculos com intersecções entre todos - vai ajudar a compreender).
-Dessa forma, na hora de somar [(18-x) + (24-x) + ___= 48], [você tem que considerar na ___ todo o grupo do "rabo curto" = 12] + [o que ainda falta, que é a intersecção X (vide os três círculos novamente)]. Aí você vai achar -x+54 = 48
OBS: Para ajudar a resolver essa questão, faça os três círculos (três grupos), com suas respectivas intersecções explanadas no enunciado. Vai preenchendo com as informações que você tem e coloca um x no que você não tem.
48 (Pretos(P) U Rabos curtos(RC) U Pêlos longos(PL)) = 24 (P) + 12 (RC) + 30 (PL) - 2 (P(Intersecção)RC(Intersecção)PL) - 4 (RC(Intersecção)PL) - 4 (P(Intersecção)RC) - (?) P(Intersecção)PL
Resolvendo isso...
48= 24+12+30-2-4-4- x(P(Intersecção)PL)
P(Intersecção)PL= 8
PRETO 6
RC 10
PL 6
GAB - CERTO
eu sou uma negação em lógica eu entendi a resolução ...
o que eu não consigo entender é
por que que se eu fizer
30 (PL) + 24(P)+ 12(RC) =66
66-48 total) = 18
18 - 2 -4 -4= 18- 10= 8
o que me confundiu foi uma outra questão que fiz que a resolução era dessa forma :
https://www.qconcursos.com/questoes-de-concursos/questao/ba8152ce-9a
não entendo pq funciona em uma e não funciona em outra
Tenho a mesma dúvida da colega Matilda:
Por que não podemos resolver pela fórmula: Total P + Total RC + Total PL - P inter RC - RC inter PL - PL inter P (x) + P inter RC inter PL ?
O resultado da x = 12, ou seja, o gabarito seria ERRADO.
No meu a intersecção deu 6 e não 8. Ou será que entendi errado ?
A questão para mim contava os gatos só pretos+ só de pelos longos + os pretos e de pelos longos. Não interpretei de maneira correta
VOU TENTAR EXPLICAR PASSO A PASSO !!!
Via de regra, em questões de conjuntos numéricos com 3 variáveis, podemos desenhar 3 esferas colocando-as em interseção da seguinte forma:
Pense que as variáveis A , B e C são os grupos e suas respectivas interseções serão AB, AC, BC; além disso, poderemos ter uma intersecção tripla que chamaremos de ABC.
A resolução padrão deste tipo de questão será :Devemos retirar as " duplas contagens" e depois somarmos cada região do desenho igualando-as ao total. Ex: retiramos ABC da região AB, da região AC e da região BC ( a fim de obtermos o que é apenas desta área- sem repetição ) e após isso , retiramos a nova região (AB, AC e BC) e ABC dos conjuntos A, B e C. Dessa forma, teremos regiões sem dupla contagem, assim basta somarmos tudo e igualar ao total.
Para a questão em tela !!! O procedimento será diferente !!! por quê ? A resposta está no português da questão ! note:
Quando o enunciado diz: (( 4 são pretos, têm rabos curtos e não têm pêlos longos; •4 têm rabos curtos e pêlos longos e não são pretos; ))
Ele está querendo te dizer que a interseção tripla não irá ser descontada das interseções duplas, visto que os 2 cães pretos, de rabo curto e pêlo longo já estão excluídos das interseções duplas, por isso o enunciado disse " não têm pêlo longo... não são pretos "
Assim: teremos 24 ( pretos ) + 12 ( rabo curto ) + 30 ( pêlo longo ) - 4 ( interseção preto e rabo curto ) - 4 ( interseção rabo preto e pêlo longo ) - 2 ( inteserção tripla ) - x ( inteserção preto e pêlo longo ) = 48
[ 24 + 12 + 30] + [ - 4 - 4 - 2 - x ] = 48 ; 66 - 10 - x = 48 ; 56 - x = 48 ;; x = 8
Note que X = 8 NÃO É A RESPOSTA FINAL !!! pois, 8 corresponde aos cães pretos e de pêlo longo incluídos aí a interseção tripla ! para acharmos aqueles que pertencem apenas à interseção de pretos com pêlo longo, basta fazermos 8 - 2 = 6 ( ESSA SIM É A RESPOSTA CORRETA ) e torna o item verdadeiro !!!
Espero ter ajudado.
1º (24+30+12) = 66 total "falso"de cães
2º (66 ''total falso"- 48 "total real") = 16 "cães que tem mais de uma caracteristica ou intersecção total"
3º Somar as Intersecções informadas na questão: (Preto + Rabo curto)+(Rabo curto+Pelo longo)+(Preto+Rabo curto+Pelo longo): 4+4+2 = 10
4º Subtrair Intersecção total - Intersecções informadas na questão: 16-10 = 6 (Preto+Pelo Longo)
Resposta : 6 "Intersecção que falta, ou seja, cães abrigados que são pretos, têm pêlos longos mas não têm rabos curtos"
Atenção pessoal... Valéria errou logo na segunda conta (66-48=18). Nesse raciocínio dela a resposta seria 8 e estaria errada.
Já fiz de tudo e não encontrei o mistério. A conta não bate.
Resolução visual da questão através de conjuntos. Fica fácil.
http://beijonopapaienamamae.blogspot.com/2010/10/dia-07-de-outubro-questao-280.html
1- descobrir o valor real de pretos e rabos curtos ... 4-2 (interseção tripla) = 2
2- descobrir o valor real de rabos curtos e pelos longos ... 4-2 (interseção tripla) = 2
3- descobrir quantos são só rabos curtos ... 12-2-2-2 (total de rabos curtos menos todas as interseções) = 6
4- subtrair do total real (48) só os rabos curtos ... 48-6 = 42
5- subtrair da sobra do total real (42) o total de pretos ... 42-24 = 18 (sobra para os pelos longos)
6- subtrair da sobra do total real (42) o total de pelos longos ... 42-30 = 12 (sobra para os pretos)
7- a interseção entre pelos longos e pretos deverá ser um número comum para que o total de pelos longos seja 30 e o total de pretos seja 24 ... 18+2+2 = (22+8 = 30) e 12+2+2 = (16+8 = 24)
8- descobrir o valor real da interseção de pelos longos e pretos = 8-2 (interseção tripla) = 6
Fiz a resolução online, tentei fazer de forma simples.
Vejam que eu continuei mesmo após achar o resultado, com a finalidade de garantir a resposta certa, fazendo a soma de tudo no final
Segue o link da resolução passo-a-passo:
https://sketchtoy.com/68777450
Olá pessoal, achei esta resolução bem detalhada no link:
https://apoioengenhariacivil.blogspot.com/2018/01/questao-raciocinio-logico-matematico-prf.html
VALE A PENA CONFERIR!
Pense: A intersecção de A e C, do conjunto universo A,B,C é igual a diferença do conj. universo menos a soma de A e C, menos o conj B.
24+30-12=42
42-48=6
pra mim o único jeito que acho o gabarito dessa questão é resolvendo por equação de primeiro grau, por diagrama de Venn só consigo achar 8
GAB: C
Galera essa questão se resolve pelo diagrama de venn onde vc faz os 3 conjuntos e começa pela interseção.
Quando vc preencher tudo , vai ver que exatamente a parte que a questão quer saber (não está preenchida).
A logica é que como vc ja preencheu tudo a unica forma de descobrir o resultado é somando tudo e diminuindo pelo total que da 6.
54-48=6
DICA: Quando a sua soma não bater com o resultado que a questão dá, EX: sua soma deu 54 mas a questão disse 48, vc automaticamente já deve subtrair para obter o resultado.
A grande sacada esta em colocar os valores em seus devidos universos.
Façam o diagrama e observem as interseções. Vocês sabem fazer, só não prestaram atenção!
Considere que em um canil estejam abrigados 48 cães, dos quais:
• 24 são pretos;
• 12 têm rabos curtos;
• 30 têm pelos longos;
• 4 são pretos, têm rabos curtos e não têm pelos longos;
• 4 têm rabos curtos e pelos longos e não são pretos;
• 2 são pretos, têm rabos curtos e pelos longos.
Matilda Bonitosa, seu raciocínio está certíssimo!
Acredito que essa questão possui mais de uma opção de resolução, as informações dão margem a no mínimo dois resultados diferentes e um deles é o que você encontrou, pois fiz conforme o professor do estratégia concursos me ensinou também, é exatamente como você fez.
y+x+6=24
z+x+6=30
30-24=6
Correto
Fiz por tentativa e erro.
Achei mais fácil
depois de montar o diagrama eu fiz a subtração entre os cães pretos e de pelos longos para obter a intersecção dos conjuntos.
deu 6, gabarito correto
Soma tudo e iguala a 48.
(18 – x) + (24 – x) + 2 + x + 4 + 4 + 2 = 48
42 – 2x + x +12 = 48
42 – x + 12 = 48
x = 54 – 48
x = 6
Apliquei o cálculo correto e consegui.
É só irem na parte que fala "Fórmula da união de 3 conjuntos"
https://www.centralexatas.com.br/matematica/teoria-dos-conjuntos/formulas#:~:text=Diagramas%20de%20Venn%20s%C3%A3o%20representa%C3%A7%C3%B5es,poss%C3%ADveis%20rela%C3%A7%C3%B5es%20l%C3%B3gicas%20entre%20conjuntos.&text=F%C3%B3rmula%20da%20Uni%C3%A3o%20de%20dois,n(A%20%5Ccap%20B)
Para ajudar os que gostam de coisas objetivas, a intersecção entre cães pretos e de pelos longos era o número "4".
boa sorte.
Fórmula União de 3 conjuntos
n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n (A ∩ B) – n (A ∩ C) – n (B ∩ C) + n (A ∩ B ∩ C)
Resposta:
48 = 24+12+30-(4+2)-(4+2)-(x+2)+2
48 = 54-x
x = 54-48
x = 6
O que não entendo é isto : Se x= 12 , segundo usando a fórmula e colocando os valores e fazendo as devidas proporções , o total vai dar 48 tbm. Nas intersecções ficaria P e PL = 10 , P e RC = 2, PL e RC = 2 e P e PL e RC = 2
Uma escola realizou uma pesquisa sobre os hábitos alimentares de seus alunos. Alguns resultados dessa pesquisa foram:
• 82% do total de entrevistados gostam de chocolate;
• 78% do total de entrevistados gostam de pizza; e
• 75% do total de entrevistados gostam de batata frita.
Então, é CORRETO afirmar que, no total de alunos entrevistados, a porcentagem dos que gostam, ao mesmo tempo, de chocolate, de pizza e de batata frita é, pelo menos, de
Temos que:
AUBUC = [n(A) + n(B) + n(C)] - n(AUBUC) - n(A^B^C)
100% = [82 + 78 + 75)%] - n(100)% - n(A^B^C)%
100 = (235 - 100) - n(A^B^C)
100 = 135 - n(A^B^C)
100 - 135 = - n(A^B^C)
-35% = -n(A^B^C) à35%
= A^B^C.
Letra C.
Inicialmente devemos nomear as incógnitas da equação da questão:
x = pessoas que gostam de pizza.
y = pessoas que gostam de chocolate.
z = pessoas que gostam de batata frita.
w = pessoas que gostam de chocolate e batata frita.
s = pessoas que gostam de batata frita e pizza.
v = pessoas que gostam de chocolate e pizza.
d = pessoas que gostam ao mesmo tempo de chocolate, pizza e batata frita.
Agora que já sabemos quais são as incógnitas, vamos escrever as equações:
Gostam de chocolate: Selecionaremos todas as variáveis que possuem chocolate:
y + w + v + d = 82%
Gostam de pizza: Selecionaremos todas as variáveis que possuem pizza:
x + s + v + d = 78%
Gostam de batata frita: Selecionaremos todas as variáveis que possuem batata frita:
z + d + s + w = 75%
Agora vamos realizar a soma das equações das pessoas que gostam de chocolate com as pessoas que gostam de pizza:
y + w + v + d + x + s + v + d = 82% + 78%
y + w + v + d + x + s + ( v + d ) = 160% → Veja que y + w + v + d + x + s = 100% de pessoas.
100% + v + d = 160%
v + d = 160% - 100%
v + d = 60%
Some as equações gerais com a equação referente às pessoas que gostam de batata frita (v + d = 60%):
z + d + s + w + v + d = 75% + 60%
z + d + s + w + v + (d) = 135% → Observe que z + d + s + w + v = 100%.
100% + d = 135.
Obtemos, então, o sistema:
v + d = 60% → Primeira equação
100% + d = 135% → Segunda equação
Resolvendo a segunda equação, obtemos:
100% + d = 135%
d = 35% → Pessoas que gostam ao mesmo tempo de chocolate, batata frita e pizza.
Substituindo o valor de d na primeira equação, temos:
v + d = 60%
v + 35% = 60%
v = 25% → Pessoas que gostam de chocolate e pizza.
A resposta correta para essa questão é a alternativa “c”.
Pense assim:
Se 82% gostam de chocolate, 18% NÃO gostam.
Se 78% gostam de pizza, 22% NÃO gostam.
Se 75% gostam de batata frita, 25% NÃO gostam.
Para resolver, basta somar a porcentagem de pessoas que não gostam de chocolate, pizza e batata ( 18% + 22% + 25%) e subtrair do total de pessoas (100%) para achar o porcentagem que gosta dos 3.
18 + 22 + 25= 65%
100%-65%= 35% (resposta correta)
Se A, B e C são conjuntos não vazios, sendo N(X) = número de elementos do conjunto X, é CORRETO afirmar que das afirmativas abaixo:
I. A ∩ (B ∪ C ) = (A ∩ B) ∪ (A ∩ C)
II. N (A ∩ B) = N (A ∪ ) - N (A) + N(B)
III. Se A ∩ B = Ø , então, obrigatoriamente, A = B = Ø

Fiz com o uso de diagramas e fica mais fácil de compreender
Se P, M e N são conjuntos e x é tal que x ∉ P ∪ M ∪ N , então
nao entendi...
Se P, M e N são conjuntos e x é tal que x ∉ P ∪ M ∪ N quer dizer q x nao ta na interseção (ou uniao) dos tres. Mas pode estar na uniao de dois desses tres conjuntos ou em apenas um conjunto, sem interseção uniao com nenhum.
entao descartei a A, pois disse q ele nao pertence a p E nem a m E nem a n. Ou seja, ele é um ponto fora dos conjuntos (o q nao é totalmente inlogico, mas achei meio forçado, ja q no enunciado nao da margem pra entender q tem algo fora
Ae fui de b, que diz que x faz parte de p OU m OU n (teria ou interseção de pelo menos dois deles, mas mesmo sem isso ja é ramim a melhor opção).
Onde errei ?
Ou a questao q é ruim mesmo ?
Diego,
Em primeiro lugar , interseção é diferente de união. A união é a soma dos conjuntos e a interseção é o que eles têm em comum. É importante que você tenha isso bem claro!
Se ele afirma que x ∉ P ∪ M ∪ N . Logo na união(soma) dos três grupos não temos o elemento x, portanto ele não pode estar em nenhum dos 3.
Exemplo:
P = {1,2,3}, M = {4,6,8}, N = {10,20,30}
P ∪ M ∪ N = {1,2,3,4,6,8,10,20,30}
Imagine que o x = 15 ou qualquer outro número que não esteja na união dos três. Logo ele não estará em qualquer um dos três conjuntos. Ou em outras palavras, x ∉ P e x ∉ M e x ∉ N. Resposta Letra A
O "e" é ultilizado para se referir a intersecção, quando a resposta da letra "A" usa o "e" dá a enteder que se fala em elemento comum (intersecção), mas a questão trás o seguinte: x é tal que x não pertence P "ou" não pertence a M "ou" não pertence a N, no meu ver a resposta correta seria a letra B.
X não pertence a NENHUM elemento dos 3 conjuntos, não existe nada de X que pertença a P, M, N.
Se você utiliza o conectivo OU, dá a possibilidade de X pertencer a algum dos 3 elementos, já que, como nos ensina a Lógica, na conjunção OU basta que um elemento seja verdadeiro, e todo o resto será também. (EX: FvFvFvFvFvFvFvFvV = Verdadeiro.) Logo não se usa OU.
Sobra então o E, já que neste conectivo, basta que um elemento seja falso, e todo o resto também será. (EX: V^V^V^F = Falso). Logo, se algum X pertencer a P, M ou N, então ja será suficiente para tornar Falso a Questão quando diz que X Não pertence a Uniao de P, M e N.
Gabarito = A
Dados fornecidos pelo item:
• P, M e N são conjuntos;
• x é tal que x ∉ P ∪ M ∪ N.
Perceba que o examinador está querendo que o candidato descubra qual é o conjunto descrito nas alternativas que satisfaça as regras impostas no enunciado.
Lembre-se que a união é a soma de todos os conjuntos, assim, quando o examinador diz que: P ∪ M ∪ N, ele está querendo dizer que nesse conjunto está contida a soma de todos os elementos dos conjuntos P, M e N.
Ao informar que x ∉ P ∪ M ∪ N, ele está querendo informar que não temos elementos de x em nenhum dos conjuntos P, M e N.
Assim, analisando as alternativas, perceba que a letra A: x ∉ P e x ∉ M e x ∉ N, nos fornece o item correto, pois esse conjunto nos mostra que não temos elementos de X em nenhum dos três conjuntos (P, M e N).
Resposta: D
Dos 420 detentos de um presídio, verificou-se que 210 foram
condenados por roubo, 140, por homicídio e 140, por outros crimes.
Verificou-se, também, que alguns estavam presos por roubo e
homicídio. Acerca dessa situação, julgue o item seguinte.
Menos de 60 dos detentos estavam presos por terem sido condenados por roubo e homicídio.
Sabemos ainda que:
O presídio continha 420 detentos
A + B + C + D = 420 (equação 1)
140 foram condenados por outros crimes
D = 140 (equação 2)
210 foram condenados por roubo
A + B = 210 (equação 3)
140 foram condenados por homicídio
B + C = 140 (equação 4)
Substituindo os valores de D e de A + B das equações 2 e 3 na equação 1, temos:
A + B + C + D = 420Substituindo o valor de C na equação 4, temos:
B + C = 140Substituindo o valor de B na equação 3, temos:
A + B = 210Assim, temos:

Mariana, parabéns pela didática na explicação !
Força e fé a todos !
Eu fiz de forma simples.
140 (roubo) + 140 (homicídio) = 350
350 - 420 (total de detidos) = 70
420 = (210 -X) + X +(140 -X) + 140
420 = -X + 490
X = 490 - 420
X= 70
Gab. errado, com o desenho de conjuntos fica melhor, mas enfim tai...
Alguem mais acha que esta questão cabe recurso de ANULAÇÃO?
Vejam meu raciocínio:
1) Temos então 3 conjuntos: R, H e O, sendo estes os conjuntos formados pelos detentos presos por Roubo, Homicídio e Outros crimes, respectivamente.
2) Pela senteça "Verificou-se, também, que alguns estavam presos por roubo e homicídio", conclui-se que a interseção dos Conjuntos R e H é NÃO VAZIO, ou seja existem elementos em comum;
3) O enunciado afirma que 140 detentos cometeram outros crimes. Mas não deixa claro que cometeram APENAS outros crimes. Logo, a interção dos conjuntos O e R, bem como dos conjuntos O e H, PODE (e pode sim, pelo enunciado) ser também não Vazio.
Chega-se fácil ao gabarito considerando que os 140 cometeram apenas outros crimes, OK... Mas que ela cabe recurso de anulação, cabe!!
Indiquem para comentário!
Gab E
Total 420 detentos
Furto 210
Homicídio 140
Outros crimes 140
Somando tudo : 210 + 140 = 350 + 140 = 490
Logo vou subtrair 490 - 420 = 70 presos.
Temos os 3 conjuntos abaixo:
Foi dito que n(Total) = 420, n(Outros crimes) = 140, n(roubo) = 210 e n(homicídio) = 140. Foi dito também que há intersecção entre os conjuntos Roubo e Homicídio, ficando implícito que não existe essa intersecção com o conjunto Outros crimes.
Como 140 cometeram apenas outros crimes, então 420 – 140 = 280 cometeram roubo, homicídio ou ambos. Isto é,
Vejamos o item:
Menos de 60 dos detentos estavam presos por terem sido condenados por roubo e homicídio.
Item ERRADO. Como vimos acima, 
Resposta: E
Fórmula da interseção:
Inters. = resto + individuais - coletivo - total
Inters. = 140 + (210 + 140) - 0 - 420
Inters. = 70
Resto: é o que não está inserido em nenhum dos conjuntos
Individuais: é o que aparece na questão dando valor a cada conjunto como no exemplo em questão
Coletivo: são os elementos inseridos em dois conjuntos
Total: são todos os elementos presentes nos conjuntos + o resto
Resolução da questão
https://youtu.be/7gxRowT1N7I
GAB: E
ROUBO=210
HOMICÍDIO=140
210+140=350
420-350=70
Muito fácil. Basta somar todas informações (roubos + homicídios + outros crimes) e subtrair o total de detentos. Ou seja:
210 + 140 + 140 - 420 = 70
Alguém me dá uma luz...
Não entendi por que algumas pessoas estão considerando que não há possibilidade de que alguém tenha cometido outros crimes e homicídio (O e H) ou de que tenha cometido outros crimes e roubo (O e R). Acho que a questão não dá dados suficientes para entendermos que cometer outros crimes implica necessariamente em não ter cometido os outros dois.
420 = (210-x ) + x + (140- x) + 140
X = 70 , gabarito errado
soma todos os crimes(da igual a 490), e subtrai dos detentos do presídio(igual a 420), logo, o número de detentos condenados por roubo e homicídio é igual a 70. Por isso, o gabarito está errado.
#FOCONAMISSÃO!
#FÉEMDEUS!!!!
SUBTRAI: roubo - homicídio e obtém a intersecção dos conjuntos que dá 70
210-140= 70
gabarito errado
Analisei da seguinte forma:
Total: 420 presos
Roubo = 210
Homicídio = 140
Outros crimes = 140
Somando Roubo + Homicídios = 210+140 = 350
Subtraindo o Total - Outros crimes = 420 - 140 = 280
Subtrai o Roubos e Homicídios - o Total e Outros Crimes = 350 - 280 = 70(Interseção)
ERRADO
Resolução em vídeo:
https://www.youtube.com/watch?v=7gxRowT1N7I&ab_channel=DanteDerette
Roubo = 210
Homicidio = 140
Outros crimes = 140
Simples, pega todos esses valores e some ficando = 490. (210+140+140). O total de detentos na questão é 420 (Opa, mas só tem 420 detentos e somando tudo vai dar 490?)
É porque alguém estamos contando duas vezes que é a minha interseção, ou uma coisa ou outra, certo?
Então é só pegar o valor somado de 490 e subtrair pelo total que é 420, ficando assim: 490 - 420 = 70.
Na questão pede-se menos de 60, portanto gabarito ERRADO.
420 = (210 - x) + x + (140 - x) + 140; x = 70 ( Em que x é a interseção Roubo/homicídio)
Gabarito:Errado
Principais Dicas:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
não seria mais fácil dessa forma; Roubo e Homicídio / 210 - 140 = 70...???
Se X e Y são conjuntos tais que, X possui exatamente vinte elementos e Y possui exatamente sete elementos, então pode-se afirmar corretamente que
Se o conjunto Y tiver todos os elementos em comum com o conjunto X, a interseção terá 7 elementos. Se tiverem menos elementos em comum, a interseção terá menos elementos. Logo, letra B)
Sobre os conjuntos X, Y e Z, possuindo respectivamente 2, 4 e 8 elementos, podemos afirmar corretamente que
Considerando que os elementos de X e Z sejam diferentes entre si, a união entre eles resulta em um conjunto de 10 elementos (se tiverem elementos em comum a união terá menos de 10 elementos, pois elementos repetidos não são considerados). Entre X∪Z (10 elementos) e Y (4 elementos), o máximo de elementos em comum que ambos possam ter é 4, pois é o tamanho do conjunto Y.
Letra C)
Os conjuntos X = {0,4,5,6,7,x} e Y = {1,3,6,8,x,y} possuem o mesmo número de elementos e X ∩ Y = {2,6,7}. Para os elementos x e y, o valor numérico de 7x – 2y é
X ∩ Y significa ???????
Leia-se X &cap Y como sendo X ∩ Y
Considere o conjunto
C = {2, 8, 18, 20, 53, 124, 157, 224, 286, 345, 419, 527}. O número de subconjuntos de três elementos de C que possuem a propriedade “soma dos três elementos é um número ímpar” é
Existem duas possibilidades da soma ser um número ímpar:
ímpar+par+par ( 1 ímpar e dois pares ) ou ímpar+ímpar+ímpar ( 3 ímpares ).
No conjunto dado existem 7 pares e 5 ímpares, então o número de maneiras da 1 opção é igual a combinação de 7 números pares tomados 2 a 2 vezes os 5 impares e o número de maneiras da 2 opção é igual a combinação de 5 elementos tomados 3 a 3:
5×C 7, 2 => 5×21= 105 maneiras
C 5, 3 => 10 maneiras
Soma-se as maneiras: 105+10= 115 maneiras no total.
Sejam ƒ e g funções cujo domínio é o conjunto D= { n ∈ IN/ n ≥ 3 } onde n representa o número de lados de um polígono regular. As funções ƒ e g associam respectivamente para cada n ∈ D , as medidas dos ângulos interno e externo do mesmo polígono .
É correto afirmar que:
Questão demorada... reserve uns 10 minutos pra fazer
Se você NÃO souber logaritmos,polígonos, fatorial ou funções, nem tente fazer agora essa questão, deixe pra depois
GAB D
Questão legal de se fazer, tem q ir analisando opção por opção.
como disse o carinha ae, se n souber essas matérias nem tente, estude elas e ai sim faça a questãooooooo
Numa pesquisa sobre leitores dos jornais A e B, constatou-se que 70% leem o jornal A e 65% leem o jornal B. Qual o percentual máximo dos que leem os jornais A e B?
RESOLUÇÃO:
1ª Interpretação:
Supondo que existem pessoas pesquisadas que não leem o jornal A e nem o Jornal B (o que contraria o enunciado), temos a seguinte solução:
Seja n o número de leitores do Jornal A e do Jornal B. Então:
• Leitores apenas do jornal A: (70% - n)
• Leitores apenas do Jornal B: (65% - n)
• Pesquisados que não leem A e nem B: x %
n +(70% - n) + (65% - n) + x % = 100% ⇔ n = 35 % + x % .
Como x % é no máximo 30 % (na condição B A ⊂ ) então o valor máximo de n é 65%.
2ª Interpretação:
Seguindo rigorosamente o descrito no enunciado, “numa pesquisa sobre os leitores dos jornais A e B”, todos os entrevistados leem os jornais A e B. Portanto, não faria sentido dizer que apenas 70% leem o jornal A e 65% leem o jornal B. Nesta situação, não haveria resposta correta.
3ª Interpretação:
Flexibilizando o enunciado para: “numa pesquisa sobre os leitores dos jornais A ou B”, poderíamos concluir que:
Se A é o conjunto de leitores do Jornal A, e B é o conjunto dos leitores de B, temos:
A ∪ B = 100%
n(A ∪ B)= n(A) + n(B) - n(A ∩ B)
n(A ∩ B) n(A) + n(B)- n(A ∪ B) = 70%+ 65% - 100% = 35%
Neste caso não faria sentido perguntar sobre o percentual máximo.
Essas interpretações foram possíveis em virtude do erro no enunciado da questão proposta. Acreditamos que a solução esperada pelo examinador é a apresentada na primeira interpretação, e é provável que ele quisesse se referir a “uma pesquisa com leitores” e não “leitores dos jornais A e B”. Sendo assim, esta questão é passível de anulação.
Resposta: C (Passível de anulação)
FONTE: http://www.sistemaeliterio.com.br/wp-content/uploads/2014/10/2011_1_FASE_Completo.pdf
Um instituto de ensino oferece três cursos profissionalizantes: de contabilidade, de informática e de administração. As matrículas dos alunos desse instituto estão assim distribuídas: 100 em contabilidade, 70 em informática, 55 em administração, 30 em contabilidade e informática e 25 em informática e administração. Com base nessas informações e sabendo que nenhum aluno está matriculado, ao mesmo tempo, nos cursos de contabilidade e administração, julgue os itens que se seguem.
A quantidade de alunos matriculados apenas no curso de administração é igual ao dobro da de alunos matriculados apenas em informática.
GABARITO CORRETO.
Somente em Contabilidade = 70
Somente em Informática= 15
Somente em Adm= 30
Contabilidade e Informática= 30
Contabilidade e Adm= 0
Administração e Informática = 25
Contabilidade, Informática e Adm não foi dado, logo presume-se que seja zero.
Pessoal, os colegas responderam bem a questão, só gostaria de contribuir com um ponto que não foi esclarecido por eles.
Em relação à interseção de Informática, Contabilidade e Administração, isto é, estar matriculados nos 3 ao mesmo tempo, foi dado na questão que NENHUM aluno estava matriculado em Contabilidade e Administração. Logo, podemos concluir que:
Contabilidade e Administração = 0
Contabilidade e Administração e Informática = 0
Isso porque essas são as duas possibilidades de ser matriculado em Contabilidade e Administração ao mesmo tempo. Não tem como existir alunos matriculados nos 3. Por isso a interseção dos 3 é 0.
Sabendo-se que o conjunto X é dado por
X = {x ∈ R ¦ x2 – 9 = 0 ou 2x – 1 = 9}
e o que o conjunto Y é dado por
Y = {y ∈ R ¦2y + 1 = 0 e 2y2 – y – 1 = 0},
onde R é o conjunto dos números reais, então pode-se afirmar que:
Gente, me ajuda que eu não entendi uma coisa:
X 2 - 9 = 0
X 2 = 9
x = raiz quadrada de nove = 3
E por que o resultado é -3 ????
de onde saiu esse -0 ?
Irei apresentar minha solução ao problema, uma vez que pode esclarecer àqueles que não conseguiram visualizar a resposta com clareza conforme a explicação do colega abaixo.
A questão desenvolver-se-á em três passos:
1) Resolução dos conjuntos individuais
2) Análise do comando da questão
3) Averiguação das respostas finais.
1) Resolução dos conjuntos iniciais.
Começando por X.
X = {x ∈ R ¦ x2 – 9 = 0 ou 2x – 1 = 9}
Legenda: V= Raíz
x²-9=0
x²=9
x=V9
x= + - 3 ( Irão me perguntar, por quê + -3 adelmo? Respondo: Quanto é -3 x -3 ? Quanto é 3 x 3? Percebo que ambos os números confirmam um mesmo resultado, que é 9)
2x-1=9
2x=10
x=5
Logo, as respostas em X são 3,-3 e 5. Perceba que o conectivo ou representa UNIDO, união. Todas as respostas são válidas.
Partindo para Y:
Y = {y ∈ R ¦2y + 1 = 0 e 2y2 – y – 1 = 0},
2y+1= 0
2y= -1
y= -1/2
2y2 – y – 1 = 0
Agora, trata-se da resolução de uma Equação do Segundo Grau. Para resolvê-la, utilizarei de dois artifícios: 1) A fórmula de Delta 2) O método de Bhaskara
Delta = B² - 4. a . c
1-4.2.-1 = Delta
Delta = 9
Bhaskara: (-b +- VDelta) /2a = R
-(-1) + - V9 / 4 = R
R = 1
R'= -1/2
Como o conjunto traz o conectivo E, apenas os resultados iguais serão válidos. Logo, apenas -1/2 valerá como resposta.
Agora, partiremos a análise das assertivas. Percebemos que nosso resultado é X U Y = { 3, -0,5 , 3 , 5 }
Logo, a acertiva correta é a Letra C
Questão suada, porém possível!
Bons estudos.
Adelmo Ribeiro
Thiago, o "-0,5" o "-1/2"
Apenas um está em decimal e o outro em forma de fração. Portanto -0,5 = -1/2
Para sabermos os elementos de cada conjunto, vamos resolver as equações dentro e cada um.
Para o conjunto x temos duas equações, resolvendo ambas abaixo:
x2 - 9 = 0 → x2 = 9 → x = ±3
2x - 1 = 9 → x = 5
Logo X = (-3; 3; 5)
Vamos agora encontrar os elementos do conjunto Y
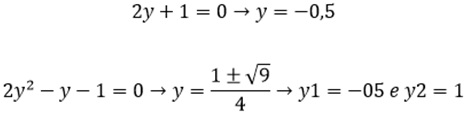
Assim, Y = (-0,5). Obs, o número 1 não entra, pois o conectivo E, exclui o mesmo. Assim fazendo X U Y obtemos(-3; -0,5; 3; 5 ).
Letra C
Bati na trave!!! Quaaase!! Marquei a A, pois não prestei atenção no conectivo E :(
Vivendo e aprendendo.
pegadinha no conectivo. essa questão vai eliminar MUITO candidato desatento.
se jogarmos y=1 na equação y²-y-1=0, fica ok, pois 2-1-1=0, é verdade. Mas se jogarmos y=1 na equação 2y+1=0, teremos: 2+1=0, o que não é verdade...portanto y=1 não satisfaz a condição imposta pelo conectivo E.
Cai igual um pato.
Vejamos cada conjunto:
X = {x Є R │ x – 9 = 0 ou 2x – 1 = 9}
Podemos ler esta expressão assim: o conjunto X é formado por todos os números “x” pertencentes ao conjunto dos números Reais, desde que eles obedeçam as expressões x – 9 = 0 ou 2x – 1 = 9.
Resolvendo as duas equações:
x – 9 = 0
x = 9
x = 3 ou x = -3
2x – 1 = 9
2x = 10
x = 5
Portanto X = {-3, 3, 5}.
Y = {y Є R │2y + 1 = 0 e 2y – y – 1 = 0}
Resolvendo as duas equações:
2y + 1 = 0
2y = -1
y = -1/2
2y – y – 1 = 0

y = 1 ou y = -1/2
Observe que no conjunto Y temos um “e” entre as duas equações. Ou seja, só devemos considerar os valores y que resolvem uma E TAMBÉM a outra equação. Neste caso, apenas o y = -1/2 resolve as duas equações (no conjunto X tínhamos um “ou” entre as equações, e foi por isso que consideramos todas as soluções das duas equações). Por isso,
Y = {-1/2}
Logo, nosso gabarito é:
X U Y = {-3; -0,5; 3; 5}
Resposta: C
https://www.tecconcursos.com.br/questoes/81407
primeira vez na vida que vejo '0' com sinal kkk
Sejam A, B e C conjuntos tais que: A = { 1, { 1,2}, { 3} } , B = {1,{2},3} e C = { { 1},2,3}. Sendo X a união dos conjuntos (A-C) e (A-B), qual será o total de elementos de X?
A-C = A
A-B= A
X é a união das diferenças, logo, será o próprio conjunto A, que tem 3 elementos. LETRA C
A - C = { 1, {1, 2} , {3} }
A - B = { {1, 2} , {3} }
A união é a soma de todos os elementos.
Logo, (A-C) U (A-B) = { 1, {1, 2} , {3} }
No total, 3 elementos.
Gabarito letra C.
Em informática, o bit foi criado como um padrão
conveniente, para representar a diversidade presente em um
conjunto que inclui apenas duas mensagens igualmente prováveis,
que podem ser identificadas a partir de uma única pergunta do tipo
“sim ou não”. Assim, em um grupo formado por duas mensagens,
A e B, que têm as mesmas chances de ocorrência, para identificar
qualquer uma delas, escolhida ao acaso, basta uma única pergunta
do tipo “sim ou não”; em consequência, diz-se que cada uma delas
tem uma quantidade de informação igual a 1 bit. Já em um conjunto
mais variado, formado, por exemplo, por 4 mensagens
equiprováveis A, B, C, D, é possível identificar uma mensagem
escolhida ao acaso, com base em duas perguntas do tipo “sim ou
não”. Basta separar o conjunto em duas metades e identificar, com
uma pergunta, a parte em que se encontra a mensagem escolhida;
recorrendo-se a outra pergunta do mesmo tipo, será possível
descobrir exatamente a mensagem referida. Nesse caso, diz-se que
cada uma das mensagens tem 2 bits de informação. Raciocinando-se
de modo semelhante, conclui-se que, em um repertório de 8
mensagens, a quantidade de informação de cada uma delas é igual
a 3 bits; se forem 16 as mensagens equiprováveis, cada uma terá 4
bits, e assim por diante.
Embora o número n de mensagens não seja, necessariamente, igual a uma potência inteira de 2, ainda assim é possível medir a quantidade k de informação, em bits, procurando-se o número k tal que
Resposta B,
para os que não são assinantes.
1) 4 mensagens = 2 bits;
2) 8 mensagens = 2,66 bits;
3) 16 mensagens = 4 bits;
n = mensagens
k = bits;
fazendo cada alternativa, utilizando a 1ª e 3ª linha, a única que fechará a conta é a questão b, pois:
2² = 4 mensagens;
2^4 = 16 mensagens.
Acredito que o gabarito seja D.
n = número de mensagens
k= número de bits
ele me disse no enunciado que pra 2 mensagens eu tenho 1 bit e assim sucessivamente:
para
n= 2 k=1
n=4 k=2
n=8 k=3
n=16 k=4 etc....
sendo assim noto que 2 elevado ao número de bits (k) será igual ao número de mensagens, portanto n = 2^k
O Tribunal de Contas do Estado decidiu oferecer a seus funcionários cursos de Inglês, Espanhol e Alemão, mas não será permitida a inscrição simultânea de Inglês e Alemão. Após as inscrições, constatou-se que
- dos 65 inscritos em Espanhol, 15 só farão esse idioma;
- 35 se inscreveram em Alemão;
- 38 se inscreveram em Inglês;
- o número de inscritos somente para os cursos de Alemão supera em 5 o número de inscritos somente para Inglês.
Nessas condições, quantos funcionários se inscreveram simultaneamente em Inglês e Espanhol?
Boa questão. A pegadinha está em perceber que os inscritos em apenas Alemão supera em 5 unidades o de inglês....e não é o quintuplo.
Assim, temos: 38 - x +35 -5 -x = 50
- 2x +68 = 50
-2x = -68 +50
2x = 18
x = 9 e portanto... 38-9 = 29
pq o total é 50?
Fiz da seguinte forma:
1) Calculei o total de alunos. Se 15 só fazem Espanhol, 35 fazem alemão e 38 fazem inglês, é só somar esses valores, que dá 88.
(explicando um pouco melhor essa parte, quando fazemos o desenho dos círculos são 7 possibilidades:
1) só fazer espanhol = 15 (enunciado)
2) só fazer inglês = x (enunciado)
3) só fazer alemão = x + 5 (enunciado)
4) fazer inglês e espanhol = 38 - x (total de alunos que fazem inglês menos os que fazem só inglês)
5) fazer alemão e espanhol = 35 - (x+5) = 30 - x (total de alunos que fazem alemão menos os que fazem só alemão)
6) fazer inglês e alemão = 0 (enunciado)
7) fazer inglês, espanhol e alemão = 0 (enunciado, pois não tem ninguém que pode fazer inglês e alemão)
assim, a soma é 15 + x + x + 5 + 38 - x + 30 - x = 88)
2) calcular o x:
x (só fazem inglês) + x + 5 (aqueles que só fazem alemão) + 65 (todos que fazem espanhol, só, ou junto com inglês ou alemão) = 88 (total calculado)
x+x+5+65=88
2x=18
x=9
3) calcular os que só fazem inglês = x = 9
4) tirar do total dos que fazem inglês, aqueles que só fazem inglês. 38 - 9 = 29.
Muito bom o exercício, mas sem desenhar é difícil explicar. Espero ter ajudado.
Legenda (faça diagrama de venn para a visualização ficar melhor)
Z --> escrintos em inglês
W --> escrintos em alemão
Y --> escrintos em alemão e espanhol
X --> escrintos em ingles e espanhol
obs.:
escrintos em ingles, espanhol e alemão = 0
escrintos em ingles e alemão = 0
equações do diagrama:
X + Y = 65 - 15
W + Y = 35 Mutiplicar os dois lados por -1
X + Z = 38
W = Z + 5
fica:
X + Y = 50
-W - Y = - 35
X + Z = 38
W = Z + 5
------------------------- somar tudo
X + Y - W - Y + X + Z + W = 50 -35 + 38 + Z +5
2X = 58
X = 29
65 inscritos em espanhol
65 - 15 = 50 inscritos em espanhol e outro idioma
35 (Alemão) + 38 (Inglês) = 73 → desses 73, 50 são inscritos em 2 cursos, logo 23 são inscritos somente em um ou outro curso
Só inglês = x
Só alemão = x+5
x+ x+ 5 = 23
2x = 18
x = 9
Inglês = 38 - 9 = 29
Alemão = 35 - (9+5) = 21
21+29 = 50
Eu fiz assim:
Como o problema não deu a intercessão, devemos considerar 100
Só espanhol= 15
alemão= 35
inglês= 38
somando 15+35+38= 88
100-88= 12
Pronto já descobrimos que a interceção é 12, agora é só subtrair do que se pede no enunciado
inglês= 38-12 = 26
espanhol= 15-12=3
logo 26+3= 29
Gabarito:D
Se você não puder se destacar pelo talento, vença pelo esforço.
Dica simples que me fez entender: DESENHEM OS 3 CÍRCULOS DE FORMA QUE DOIS APENAS SE TOQUEM não transpassando (ing e alemão) assim dá pra ver que não haverá aquele triangulo interno. Me ajudou muito.
Foi realizada uma pesquisa, com um grupo de pessoas, envolvendo a preferência por até duas marcas de carros dentre as marcas C1, C2 e C3. A pesquisa apresentou os seguintes dados:
- 59 preferem a marca C1.
- 40 preferem a marca C2-
- 50 preferem a marca C3.
- 17 preferem as marcas C1 e C2.
- 12 preferem as marcas C1 e C3·
- 23 preferem as marcas C2 e C3·
- 49 não preferem nenhuma das três marcas.
O número de pessoas que preferem apenas a marca C2 é igual a:
muita atenção no enunciado que diz "preferem apenas marca C2"
",,,enquanto eu viver vou te buscar..."
SomenteC2 = 40 -17 – 23 = 0
A chave da questão é a frase "...envolvendo a preferência por até duas marcas", ou seja, ao fazer o diagrama de venn ( 3 círculos) a área do meio que envolveria as 3 marcas será 0. Assim, com as demais informações dadas, pode-se calcular o valor de APENAS C2, que será:
40 - (17+23) = 40 - 40 = 0
Uma turma de 94 alunos discute a preferência por dois professores A e B, entre outros professores da escola. Após a discussão, registrou-se que o número de alunos que preferem o professor B era:
O quíntuplo do número de alunos que preferem A e B;
O triplo do número de alunos que preferem A;
A metade do número de alunos que não preferem A e nem B.
Nessas condições, o número de alunos que não preferem os dois professores é
Errei essa questão. Mas logo descobri o pq.
A casca de banana da questão está em apresentar, de cara, a resposta 60. No entanto, esse número se refere ao número de alunos que não preferem nem A e nem B.
Notem que a questão pede "o número de alunos que não preferem os dois professores". Isso quer dizer que não preferem os dois professores simultaneamente, ou seja, que não preferem A e B ao mesmo tempo. Dessa forma, incluem-se também os Somente A e os Somente B.
Neste caso, teríamos:
Somente A: 04
Somente B: 24
Nem A e Nem B: 60
RESPOSTA: 88
ATENÇÃO, pessoal!! É importante sempre q concluir as contas, verificar novamente o que a questão pede. ;)
Bons Estudos! =)
Muito obrigado Bruno
B=5x, AeB=x, A= B/3-AeB e 2vezesB não preferem nem A nem B, 2.5x=10x, chamaremos de C
Temos que: Só B=B-AeB _ B= 4x, Só A= B/3 - AeB _ A=5x/3 - x _ A= 2x/3
Somando: A+B+AeB+C=94
2x/3+5x+x+10x=94, 2x/3+15x=94
multiplicando os dois lados por 3, temos: 47x=282, x=6
substituindo "x" por 6 temos: B=24, A=4, AeB=6, C=60
A questão pergunta o numero de alunos que não preferem AeB, basta somar: B+A+C _ 24+4+60=88
Gabarito letra: e
e-
se A tem 3x B e AB tem 5x B, é necessario encontrar o mmc de 3 e 5. 15. Mas 15 nao se adapta ao restante do problema. Proximo é 30, o qual fecha com o requisito de haver 2x que nao sao A nem B. Logo:
A = 10 (somente A = 4)
B = 30 (somente B = 24).
AB = 6.
outros = 60.
Se o total é 94, somente 6 gostam dos 2 ao mesmo tempo. Logo, 94 - 6 = 88. 88 ou gostam somente de A, ou somente de B ou nenhum.
Com certeza a mulher do autor da questão colocou chifre nele com um analista de sistemas
A questão deseja saber B - A
Dos 250 temos 30 que não optam por A ou B, então são 220
A + B - (A interseção B) = 220
130 + 150 - x = 220
280 - x = 220
- x = 220 - 280
-x = -60 (como o sinal está dos dois lados, se transforma em positivo)
A interseção é 60 (que optam por A e B)
Apenas B: 150 - 60 = 90
TOTAL= 250
A= 130
B= 150
NEM A NEM B= 30
SOMA 130 + 150 +30 = 310
SUBTRAIR 310-250 = 60
ENCONTRADO A INTERSEÇÃO QUE É (60) FAREMOS A SUBTRAÇÃO DE ( B=150 - INTERSEÇÃO= 60 QUE DA = 90 )
T=250
A=130
B=150
C=30
250-30=220 pessoas que preferem A e/ou B
A+B= 130+150= 280
280-220= 60 que é interseção, o grupo que prefere o A e o B
A=130-60 = 70 que preferem só o curso A
B= 150-60= 90 que preferem só o grupo B
Gabarito: letra B, 90 pessoas
Questão de simples raciocínio. No momento em que o enunciado diz que ''B'' é subconjunto de ''A'', porém também ''A'' é subconjunto de ''B'', automaticamente estes dois conjuntos devem ser iguais pois é fisicamente, logicamente impossível dois conjuntos serem subconjuntos um do outro simultaneamente sendo que os dois NÃO são iguais. Logo, é possível descartar as alternativas ''B'', ''C'' e ''D''. Por fim, a alternativa correta é a letra ''A'' pois o conjunto ''B'' não é igual a ''C'', porém ''C'' é subconjunto tanto de ''A'' e ''B'.
Para resolver a questão, basta focar nesta informação: A e B possuem elementos de C, ou seja, ele é o menor de todos os conjuntos. Sendo assim, as demais alternativas estão incorretas.
Itens B e C) B não pertence a C, pois é C que pertence a B.
itens D e E) C não é igual B e B não é igual a C.
Vale ressaltar que há outros erros, mas esse é o suficiente para cortar todas as alternativas incorretas.
Em um pesquisa de associação entre a venda de feijão e de arroz, com 500 pessoas que faziam compras em um supermercado, verificou-se que 300 delas compraram feijão, 240 compraram arroz e 120 não compraram nenhum dos dois itens.
A probabilidade de uma pessoa desse grupo, selecionada aleatoriamente, ter comprado arroz e feijão é igual a
TOTAL = 500
SOMENTE FEIJÃO = 300
SOMENTE ARROZ = 240
NENHUM = 120
300 + 240 + 120 = 660
660 - 500 = 160 (COMPRARAM AMBOS)
160/500 = 32%
GAB A
NÃO DESISTA!
Foi feita uma pesquisa com 65 pessoas para saber quais comprariam os refrigerantes A e B. Verificou-se que 30 pessoas comprariam somente o refrigerante A e 17 pessoas comprariam os dois refrigerantes. Se todas as pessoas escolheram pelo menos um dos refrigerantes, então o total de pessoas que comprariam o refrigerante B é de:
Olá Angélica, Nina Rodrigues e Thaise Benoni, as três postaram comentário que erraram a qestão por falta de atenção, é interessante perceber que isso acontece naquelas questões fáceis e que acabamos a prova na certeza que acertamos. Quando vem o gabarito pimba, erramos a questão, às vezes achamos até que o gabarito está errado.
Durante uma prova o tempo voa, sem falar no tradicional nervosismo dos quinze minutos iniciais e esse tipo de falta de atenção acaba acontecendo, mas não se preocupem todos candidatos já passaram por isso, mas vou deixar três dicas que me ajudaram muito, espero que possam ajudá-las também:
1° Leiam a questão com bastante atenção, tem que está atento com o que é realmente pedido na questão;
2° Acabando a prova antes do tempo, não entregue logo, faça uma boa revisão( já salvei várias questões assim); e
3° Façam o máximo de exercícios que puderem na fase de preparação.
Grande abraço e bons estudos.
65 pessoas comprariam A e B;
Somente 30 compraram A;
17 pessoas compraram A e B;
Todas as pessoas comprariam A ou B;
Então o total que comprariam B seria:
65 (total de pessoas) - 30 (total que só comprou A) = 35 pessoas que compraram B
Fiz dessa forma e deu certo, espero ter ajudado.
Eu fiz da seguinte forma e deu certo:
Como nós já sabemos que o total de pessoas entrevistada é 65 e que SOMENTE 30 compraria a marca A, eu subtrai as 30 que só compraria a marca a do total de entrevistado e eu cheguei ao resultado que 35 compraria a marca B
Resolvi dessa forma:
Refrigerante A = 30 pessoas
Refrigerante A e B = 17 pessoas
Cálculo: 30+17 = 47 pessoas - total 65 pessoas = 18
Total de Refrigerante B = 17+18 = 35 pessoas.
Letra B
A pergunta é. Se todas as pessoas escolheram pelo menos um dos refrigerantes, então o total de pessoas que comprariam o refrigerante B é de:
E não: Se todas as pessoas escolheram pelo menos um dos refrigerantes, então o total de pessoas que comprariam SOMENTE o refrigerante B é de:
resposta: b
Foi uma pegalandro do madinha.
Numa universidade, foi feita uma pesquisa de mercado sobre a preferência de 200 estudantes por três marcas de canetas A, B e C. O resultado foi o seguinte: 20 utilizavam as três marcas, 30 utilizavam as marcas A e B, 50 utilizavam as marcas B e C, 60 utilizavam as marcas A e C, 120 utilizavam a marca A e 75 utilizavam a marca B. Se todos os 200 estudantes entrevistados deram preferência a pelo menos uma marca, sobre as afirmações,
I. 35 utilizavam somente a marca C.
II. 100 utilizavam pelo menos duas das marcas.
III. 10 utilizavam A e B e não C.
IV. 35 utilizavam a marca C e 80 utilizavam pelo menos duas das marcas.
V. 5 utilizavam pelo menos A e B e não C.
podemos concluir que
Construindo o diagrama de Venn Abaixo:
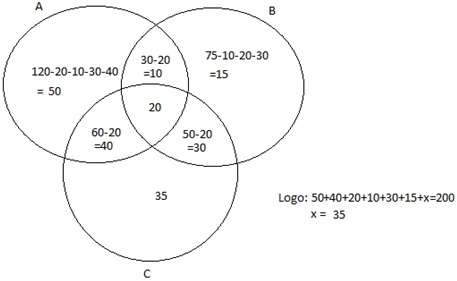
Vemos que a alternativa correta é a letra D
Sejam A, B e C três eventos em um espaço de probabilidade. O evento que ocorre quando, pelo menos, dois desses três eventos ocorrem é expresso por
Em um colégio com 520 alunos, 330 estudam inglês, 185 estudam espanhol e 63 estudam ambas as línguas. Pela teoria dos conjuntos pergunta-se: Quantos alunos não estudam nenhuma das duas línguas?

Uma escola oferece reforço escolar em todas as disciplinas. No mês passado, dos 100 alunos que fizeram reforço escolar nessa escola, 50 fizeram reforço em Matemática, 25 fizeram reforço em Português e 10 fizeram reforço em Matemática e Português. Então, é correto afirmar que, no mês passado, desses 100 alunos, os que não fizeram reforço em Matemática e nem em Português é igual a:

Caros colegas.O comentário do Diego Lima não pode ser vizualizado pq o site QC não permite mais o anexo de imagens(diferente do antigo site questoes de concursos).
Abraço!
Guerreiros, não sei se estou falando besteira mas tive uma interpretação ambígua pois, a meu ver, não fica claro se os demais alunos fizeram reforço de outra matéria ou se simplesmente não fizeram reforço nenhum, neste caso a resposta seria diferente: 25.
Desenha o Diagrama de Venn, pois ficará fácil a visualização. 50 (40 (10) 15) 25
100 - 65 = 35
ou
100 - [ 40 (50m - 10 m e p) + 15 (25p - 10 m e p) + 10 m e p ] = 35
Vanessa Yano, preste bem atenção no enunciado: "No mês passado, dos 100 alunos que fizeram reforço escolar nessa escola,(...)"
Ou seja, todos esses 100 alunos fizeram algum reforço.
Apesar de ser Esaf...a questão foi bem direta...
Uma estatística sobre o perfil dos inscritos em um concurso público revelou que 60% são homens e 40% são mulheres, entre eles 80% dos homens possuem curso superior e 30% das mulheres não possuem curso superior. Qual a porcentagem dos candidatos que já possuem curso superior ?
Pra quem tem muita dificuldade como eu em visualizar a questão - Substitua por um Valor.
Ex: 1.000 inscritos no Total.
Homens => 60% de 1.000 ====> 600 Homens inscritos (HI);
Mulheres => 40% de 1.000 ===> 400 Mulheres inscritas (MI).
Dos 600 (HI), somente 80% tem nível superior.
600 de 80% => 480 Homens com Nível Superior;
Das 400 (MI), somente 70% tem nível superior.
400 de 70% => 280 Mulheres com Nível Superior
Homens + Mulheres:
480 + 280 => 760 => Divide por 10% (Porcentagem).
Resposta: 76% (Gabarito: D)
Que DEUS nos Abençoe !!!
"O homem não pode receber coisa alguma, se do céu não lhe for dada". João 3:27
Perfeita a sua explicação Beto! Obg
Resolvi da mesma forma da Diene :)
Os torcedores de quatro clubes paulistas (corintianos, palmeirenses, são-paulinos e santistas) foram assistir a uma partida de futebol da seleção brasileira com a seguinte: distribuição:
15% eram palmeirenses;
20% eram são-paulinos;
45% não eram santistas.
O percentual de corintianos foi de
Se 45% não era Santista,
15% são Palmeirense +
20% sao São-Paulino =
-------------------------------
35%
- 45% que não são Santista.
-------------------------------------
= 10% que sobra para os Corintianos.
Depois de meia hora tentando entender vou ajudar os colegas com uma explicaçao mais clara:
se 45% NAO sao santista, significa que 55% sao santistas. dai vc trabalha com os 45% que NAO sao santistas. Desses 45% compoe 15% de palmeirenses e 20% de sao paulino, formando 35%. o resto que sobrar pra completar 45% é de corintiano que é 10%,kkkk poxa
, foi a pressa
NAO CONCORDO COM O GABARITO... ACHO QUE O SAO-PAULINO ERA PRA TER MAIOR PERCENTUAL >< KKKKKKKK...
tirando a brincadeira... essa questão é muitooo boa.. o candidato tem q mostrar jogo de cintura... Eu mesmo errei bunito :(
Caro Jean, muito obrigado. Entendi pelas suas explicações muito consistentes.
45% não eram santistas. Logo, 55% eram do santos. 15% eram palmeirenses 20% eram sp, logo, 35%. 100- 55+35 = 10%
obs.: por que usar times paulistas para MPE-AC? Eles não têm história própria?
Considere que, em um conjunto U de homens, está
indicado por A o conjunto daqueles que têm mais de 1,85 m de
altura e por B, o conjunto dos que pesam mais de 85 kg. Considere,
ainda, uma empresa de segurança verificou que havia erro no
anúncio publicado “Contratam-se homens com mais de 1,85 m de
altura ou com mais de 85 kg” e publicou um segundo anúncio com
a seguinte forma: “Contratam-se homens com mais de 1,85 m e
mais de 85 kg”.
Considerando que o conjunto U tenha 32 elementos, A tenha 20 elementos e B tenha 18 elementos, assinale a opção em que é apresentado o número máximo de homens que não poderiam satisfazer aos requisitos de nenhum anúncio.
Não entendi.
Não existe outra maneira de fazer que seja por conjuntos?
Ou outra linha de raciocínio?
Gostaria de saber como ele chegou a 12. Minha resposta deu 6 e fiquei sem entender uma coisa: ele não deu elemento algum que caracterizasse como parte do conjunto A e parte do conjunto B.
A resposta é a alternativa D. São 12 pessoas que não se encaixam em nenhum anúncio, Vejamos:
A alternativa quis saber qual o número mínimo de pessoas que pode ficar dentro do diagrama de Venn, temos A=20, b=18. Para facilitar desenho o diagrama, no meio dele (comum) coloca o menor número dado, no caso 18, depois subtraia (18 -20 =2) e (18-18=0), pronto, esse é o número minimo de pessoas dentro do diagrama, agora some esses valores, 2+0+18 = 20, logo temos 20 pessoas dentro do diagrama, mas a questão quer saber o número de pessoas que não estão no diagrama, ai é só fazer, 32-20=12. Pronto.. são 12 pessoas que não participam do anúncio.
Minha linha de raciocínio foi assim: conjunto u = total = 32. Conjunto A = 20 elementos(acima de 1,85 m); Conjunto B = 18 elementos (+85 kg). Fiz o diagrama e a interseção é x. Logo A é 20-x e B 18-x. Fazendo a equação: 20-x+x+18-x = 32, x=6. O primeiro anúncio é ou e o segundo é a soma das duas características. Se for só 1,85 temos 14 homens, se for só acima de 85 kg temos 12 homens, se for as duas características temos 6 homens. Logo 32, 6, 12 e 14 são as possibilidades.
Pois é me lasquei pois estou com a linha de pensamento errada. Não entendi mesmo essa resposta. Alguém pode me ajudar. Indicar algum vídeo ou algo parecido?
Ana licci, o que ele pede é o número máximo de homens que não poderiam satisfazer aos requisitos de NENHUM anúncio.
Vc encontrou o número de elementos que se encaixam no segundo anúncio( A inter B).
O número máximo de homens que podem não se encaixar em nenhum anuncio é = 12.
Pois não é necessário que os 32 homens do conjunto U sejam pertencentes a A ou a B. Ex: 18 pertencem a A e B, e 2 somente a A. Vai atender ao enunciado, pois A será = 20 e B= 18. Porém, de apenas 20 elementos, assim, 32- 20 = 12 o número max de os homens que não possuem nenhuma das características desejadas.
É muito difícil de tentar explicar conjuntos, mas espero ter ajudado alguém.
Eu pensei assim:
A possui 20 elementos. B possui 18 elementos.
O conjunto B pode estar todo contido em A, ou seja, os 18 homens que pesam mais de 85 kg podem ao mesmo tempo medir mais de 1,85 m.
Assim, a interseção entre A e B seria de 18 elementos, possuindo A apenas 2 elementos a mais que B. Neste caso, A U B teria um total de 20 elementos.
Logo, o máximo de homens que não se encaixariam nos anúncios seria 12.
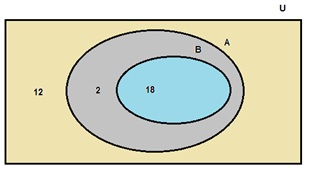
O conjunto B por ser menor, pode estar todo contido em A, somando 18 elementos de B para chegar aos 20 de A, bastam 2 elementos, logo estes fazem parte exclusivamente de A. Para completar os 32 elementos do conjunto U faltam 12 elementos, pois 18 + 2 = 20 e 32 – 20 = 12.
Questão muito similar à Q363639.
U = 32
A = + de 1,85 altura = 20
B = + de 85 Kg = 18
Anúncio 1 = +1,85 altura OU + 85Kg
Anúncio 2 = +1,85 altura E + 85Kg
Anúncio 1 = A ou B
Anúncio 2 = A e B
Como o enunciado NÃO APRESENTA, INDICA ou SUGERE que exista entre o conjunto A e B uma INTERSEÇÃO, subentende-se que trata-se de uma União dos dois conjuntos.
Onde teremos um MENOR CONJUNTO (B) contido num MAIOR CONJUNTO (A), ou seja, TODO B é A.
E só por no diagrama na seguinte ordem de prioridade:
B = 18
SOMENTE A = 2
SOMENTE U = 12
RESPOSTA: Letra d) 12.Como a questão não nos deu a intersecção, pode ser que o grupo B (18 elementos) esteja contido no grupo A (20 elementos). Logo, no mínimo 20 elementos estarão dentro do diagrama. Assim, para encontrar o número que está fora do diagrama (não preenche a nenhum dos requisitos), subtraímos 32 (número total de elementos) de 20 (número mínimo de elementos dentro do diagrama).
R é o conjunto que se deseja, que não seja (A ou B), nem (A e B):
R = U - (AUB) - AB
Então, R é o que não está dentro da bolota A nem da B =D. Sua quantidade é o "RESTO":
32 - RESTO = 20 + 18 - AMBOS
RESTO = AMBOS - 6
A questão pede que Resto seja o máximo possível, logo AMBOS também terá que ser o máximo possível,
então AMBOS tem que ser o menor entre os dois conjuntos (18)
RESTO = 18 - 6
RESTO = 12
De forma mais simples, pra quem tem um contato maior com esse tipo de questão, basta somar os valores individuais, subtrair com o valor total, pronto, achamos a interseção(6), multiplique-a por 2, já que estamos falando das opções que não poderiam satisfazer aos requisitos de nenhum anúncio, finalmente, chegamos no valor da resposta. Letra D
A melhor maneira de se fazer é pelo metodo do nosso amigo ai Renato Tanner. Se vcs montarem o conjunto, vão ser que é bem facil!! Boa sorte
Acabei de aprender uma melhor forma de resolver este tipo de questão! Através de um outro comentário....
Pegue o n° total de elementos: 32
Pegue o conjunto com maior elemento: B(20)
E apenas subtraia: 32-20= 12
Simples assim!
Fé em Deus!
Aprendi com um comentário de um colega em outra questão:
Quando ele pedir o máximo que está fora dos conjuntos - Pegue o total e subtraia ao de maior valor do conjunto apresentado, nesse caso é o 20.
Gente, eu pensei exatamente como a colega Ana Gomes. Tenho feito as questões desse jeito e até agora não tinha tido problema. Alguém sabe me dizer porque esse raciocínio está errado?
Pensei da seguinte maneira.
A (Conjunto daqueles com mais de 1,85m de altura) = 20 elementos
Se 20 homens tem mais de 1,85 de altura, 12 homens tem menos de 1,85 de altura (Uma vez que o conjunto tem 32 elementos; 32-20=12)
B (Conjunto daqueles com mais de 85kg) = 18 elementos.
Se 18 homens pesam mais de 85kg, 14 homens pesam menos de 85kg. (Uma vez que o conjunto tem 32 elementos; 32-18=14)
É só pensar pela ideia do complementar (O que falta pra completar o conjunto total?)
Em A notamos que faltou 12 elementos para completar.
Em B notamos que faltou 14 elementos para completar.
O número máximo de homens que não satisfazem os requisitos de nenhum anuncio é 12.
Sobrou dois homens no grupo B que provavelmente tem mais de 1,85m de altura.
20 + 18 - x = 32.
X = 6. (Interseção).
Temos em comum 6 elementos, em A e B. Assim, devemos subtrair 6 elementos de cada, de modo que, assim, retiramos então 12.
Gabarito: D.
Bons estudos.
Este vídeo explica como resolver esse tipo de questão de máximos e mínimos
https://www.youtube.com/watch?v=ab5xioA0_0s
TEMOS 32 total. A20+ B18= 38. Logo 38-32= 06 intersecção entre ambos.
Soma-se então, 20+18+06= 44 - 32 total= 12. Letra D.
Dados os conjuntos A = {x | x é vogal da palavra CARRO} e B = {x | x é letra da palavra CAMINHO}, é correto afirmar que A∩B tem
Considere as seguintes acepções da palavra função,
reproduzidas de três dicionários da língua portuguesa.
A: Qualquer correspondência entre dois ou mais conjuntos.
Uma relação entre dois conjuntos que satisfaça a condição da acepção C também satisfará a da acepção A.
CORRETO, pois o dicionário C afirma "relação entre dois conjuntos" e no dicionário A "relação entre dois ou mais". Sendo assim, falaram a mesma coisa, porém o A abrangeu mais a ideia.
Avante!
A={2,3,4,5} , B={2,3,4} ,isso não é função,pois existe um número em A que não tem correspondente em B , apesar de ter números de A correspondentes em B, logo não posso afirma que seja QUALQUER CORRESPONDÊNCIA ENTRE DOIS OU MAIS CONJUNTOS
É o que eu acho , se eu estiver errado me corrija por favor alguém.
A acepção da C é uma função injetora( onde todo elemento da imagem corresponde a um unico elemento do contradominio.
A acepção da A é qualquer correspondencia entre dois ou mais conjuntos, ou seja funçao injetora é uma delas portando tendo uma situação relatada na C torna a A verdade.
Gab Certo
Gabarito Certo.
O conceito de A é mais abrangente que o de C. Logo, C se insere na acepção de A.
Depois de analisar bastante, Fez sentido...
A ⊂ C
A acepção C é mais específica, ou seja, A é muito mais abrangente e abarca um número maior de possibilidades de interpretação, por isso, todas as relações entre conjuntos que satisfazerem a Concepção C, automaticamente, irão também concordar com a A ( Qualquer correspondência entre dois ou mais conjuntos.)
gabarito: CERTO
Considere verdadeiras todas as afirmações a seguir sobre os grupos A, B e C de profissionais de um estabelecimento bancário:
I. O Grupo A tem 12 elementos.
II. O Grupo B tem 11 elementos.
III. O grupo C tem 10 elementos.
IV. Apenas Ana Lúcia faz parte dos três Grupos, e todos os demais profissionais fazem parte exatamente de um Grupo.
Decorre dessas afirmações que o número total de elementos da união desses três Grupos é
n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)
n(A U B U C) = 12+11+10-1-1-1+1=31
TOTAL DA SOMA DE TODOS OS GRUPOS 33, ANA LUCIA NAO PODERA ESTAR NOS 3 AO MESMO TEMPO. -2 ENTAO RESPOSTA LETRA A 31.. A LUTA APENAS COMEÇOU..
Questão fácil, porém maldosa.
A =12 elementos, apenas A = 12 - 1 = 11 elementos
B = 11 elementos, apenas B = 11 - 1 = 10 elementos
C = 10 elementos, apenas C = 10 - 1 = 9 elementos
Total: 11 + 10 + 9 + 1 ( Ana ) = 31 elementos.
Alternativa A
A = 12 (- 1)
B = 11 (- 1)
C = 10 (- 1)
Σ = 30 + Ana Lúcia = 31
Obs. -1 se refere à Ana Lúcia que esta dentro de todos os grupos.
Questão fácil, porém maldosa!
A 1 2 3 4 5 6 7 8 9 10 11 12
B 1 2 3 4 5 6 7 8 9 10 11
C 1 2 3 4 5 6 7 8 9 10
12 + 11 + 10 = 33
DIGAMOS QUE ANA, CHAMA-SE 10. Se ela está nos 3 grupos, então vou tirar ela da SOMA dos três grupos, ok?
11 + 10 + 9 = 30
30 + a ANA = 31
esqueci de somar a aninha
Por isso acho seguro sempre colocar no desenho.
Desenhe 3 conjuntos.
A, B e C
No meio coloque 1 (Ana)
Como cada um dos demais profissionais está em exatamente um grupo, não há interseção de 2.
Logo, somente A=11
B=10
C=9
Somando todos os elementos dos conjuntos = 31.
GABARITO A
#TJSP2021
Uma turma possui 75 alunos. Desses alunos, 20 gostam de matemática, 30 gostam de química e 40 gostam de física. Sabendo, ainda, que 10 gostam de matemática e física, 15 gostam de física e química, 5 gostam de matemática e química e 10 não gostam de nenhuma dessas disciplinas, o número de alunos que gostam somente de matemática e química é:
M=20, F=40, Q=30, MeF=10, MeQ=5, QeF=15
MouFouQ = M + F + Q - MeF - MeQ - QeF +MeFeQ
MouFouQ = 75 - 10 = 65
65 = 20 + 40 + 30 - 10 - 5 - 15 + MeFeQ
MeFeQ = 5
SóMeQ = MeQ - MeFeQ
SóMeQ = 5 - 5 = 0
Letra A
até mais!
;)
Se alguém conseguiu fazer usando o diagrama de Venn, poderia demonstrar? Obrigada!
Faltou a questão por a informação de quantos alunos gostam das 3 disciplinas, pois sem ela não da pra fazer a questão.... No meu caso eu chutei como 5 e após todas as interseções vi que "5" era exatamente o número de alunos que gostam das 3 matérias e só sabendo este número que você terá meios pra solucionar a questão.... Brigado ;)
Pessoal,
Segue a resolução passo a passo no link abaixo. Espero que ajude!!!
http://imageshack.com/a/img713/636/4yjx.jpg
Bons estudos!
Gente, li os comentários acompanhada consigo fazer essa questão, mas quando tento outras parecidas complica tudo, os 5-5, alguém pode me ajudar?
Bem sacana essa questão, pois ela não afirma que existem alunos que gostam de 3 matérias ao mesmo tempo, no entanto, ela também não afirma que NÃO existem alunos que gostam de três matérias simultaneamente.
O enunciado não cita que existem alunos que
gostam das 3 disciplinas, mas também não faz menção alguma dizendo que não
existem, logo, iremos assumir que existem. Fazendo o diagrama de Venn Abaixo:
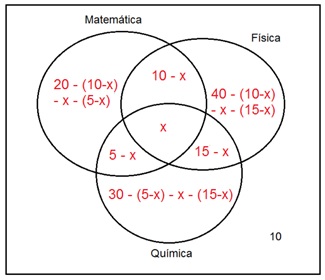
Assim temos:
M = 20 – (10 - x) – x – (5 - x) = 20 – 10 + x – x – 5 + x = x + 5
F = 40 – (10 - x) – x – (15 - x) = 40 - 10 + x – x - 15 + x = x + 15
Q = 30 – (5 - x) – x – (15 - x) = 30 - 5 + x - x - 15 + x = x = x + 10
Somando tudo e igualando ao total de alunos menos os que não gostam de nenhuma disciplina, ou seja, 75 – 10 = 65:
(M) + (F) +(Q) + (M + F) + (M + Q) + (F + Q) + (M + F + Q) = 65
= (x + 5) + (x + 15) + (x + 10) + (5 – x) + (15 – x) + (10 – x) + x = 65
x + 60 = 65
x = 65 – 60
x = 5
Logo a quantidade de alunos que gostam somente de Matemática e Química é (5 – x) = (5 – 5) = 0.
RESPOSTA: (A)
Não é necessário saber a interseção dos três: chame de x.
Assim, o número de alunos que gostam somente de química e matemática fica 5-x;
O número de alunos que gostam somente de química e física fica 15-x;
O número de alunos que gostam somente de matemática e física fica 10-x;
Os que gostam somente de matemática são m = 20-(10-x)-(5-x)-x => m=x+5
Os que gostam somente de física são f = 40-(10-x)-(15-x)-x => f=x+15
Os que gostam somente de química são q = 30-(5-x)-(15-x)-x => q=x+10
Coloque tudo isso num diagrama de venn e ponha o número 10 do lado de fora, i.e., os que não gostam de nenhuma das matérias. Somando todos os elementos, teremos 75, que é o total de alunos. Assim:
x+(5-x)+(15-x)+(10-x)+(x+5)+(x+15)+(x+10)+10 = 75
x=5
Os que gostam somente de matemática e química são (x-5). Portanto, x-5 = 5-5 = 0.
Gabarito A
Aos que tentaram explicar, me desculpe, mas ainda não entendi pq a resposta é zero, se pelo diagrama que eu fiz, deu que somente matemática são 5 e somente quimica são 10.
Daniela Matos, a questão não pergunta quantos gostam somente de matemática e somente de química. Ela pergunta quantos gostam somente de matemática e química, ou seja, pede a interseção dessas duas matérias.
Resposta A
----------------------------------------------------
A- Qual o número de alunos que gostam somente de matemática? 8 alunos
B- Qual o número de alunos que gostam somente de física e química? 18 física 13 química
C- Qual o número de alunos que gostam de pelo ao menos uma das três disciplinas? 63 alunos
D- Qual o número de alunos que não gostam de nenhuma das disciplinas citadas? 12 alunos
Importante "...pois ela não afirma que existem alunos que gostam de 3 matérias ao mesmo tempo" WagnerdosSantos
https://goo.gl/Mp99dT
#sefazal
Essa aí e difícil de mais
Não consigo entender a diferença entre "somente matemática e química" e "matemática e química"
Porque SóMeQ = MeQ - MeFeQ?
Uma empresa oferecia vagas de emprego nos estados de São Paulo e Rio de Janeiro. Os candidatos pré-selecionados poderiam escolher um ou os dois estados em que tivessem interesse em trabalhar.Sabe-se que 26 pessoas escolheram São Paulo,12 optaram pelos dois estados e 20 escolheram apenas um dos dois estados. O número de candidatos pré-selecionados foi:
dos 28 que escolheram SP, tira-se 12 que escolheram ambos. Restam 14 que escolheram apenas o estado de SP.
Assim, dos 20 que escolheram apenas um estado, tira-se 14 (que são os que escolheram o estado de SP), restando 6 que escolheram apenas o estado do RJ.
Logo:
14 candidatos escolheram apenas SP.
12 candidatos escolheram ambos estados (SP e RJ)
06 candidatos escolheram apenas RJ.
Totalizando 32 candidatos (14+12+6).
Fazendo o Diagrama de Venn, podemos entender
melhor, assim, resolvendo:
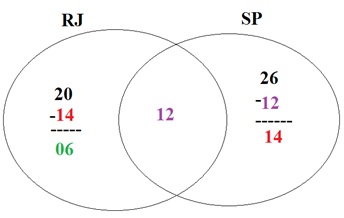
Basta agora somar: 06 + 12 + 14 = 32. Logo O número de candidatos pré-selecionados foi 32.
RESPOSTA: (A)
Uma empresa oferecia vagas de emprego nos estados de São Paulo e Rio de Janeiro. Os candidatos pré-selecionados poderiam escolher um ou os dois estados em que tivessem interesse em trabalhar.Sabe-se que 26 pessoas escolheram São Paulo,12 optaram pelos dois estados e 20 escolheram apenas um dos dois estados. O número de candidatos pré-selecionados foi:
SP: 26-12 = 14
RJ: 6
(apenas 20 escolheram uma dos 2 estados. Aqui n diz q esse estado é o RJ , mas diz q somente RJ e somente SP tem juntos 20 escolhas , e como SP já tem 14 subtraímos, 20 - 14= 6 , o numero de cancidatos do RJ)
SP e RJ: 12
Uma empresa oferecia vagas de emprego nos estados de São Paulo e Rio de Janeiro. Os candidatos pré-selecionados poderiam escolher um ou os dois estados em que tivessem interesse em trabalhar.Sabe-se que 26 pessoas escolheram São Paulo,12 optaram pelos dois estados e 20 escolheram apenas um dos dois estados. O número de candidatos pré-selecionados foi:
26 escolheram apenas SP.
12 que é a intersecção optaram pelo dois estados.
20 pessoas escolheram apenas um dos dois estados.
Então, vamos calcular o conjunto de SP: 26 -12 = 14 pessoas em SP
Para eu saber o número do conjunto do Rio de Janeiro vou pegar 20 que é o número das pessoas que escolheram pelos dois estados MENOS 14 pessoas que optaram por SP, então fica assim: 20 -14 = 6
AGORA VAMOS SOMAR TUDO : 14 DE SP + 12 INTERSEÇÃO + 6 DO RJ = 32
Espero ter ajudado alguém.
gabarito a
Algo ficou implícito para os que erraram, e com certeza deve ter sido a hora da intersecção.
A = SP = 26
A+B = SP + RJ = 12
X = representa o RJ = 20
A intersecção A+B = 14 !
A+B = 12 !
X = 20
X intersecção A (essa intersecção ocorre porque é a separação que acontecerá entre a separação de A e A+B , entendeu?! Digo , ocorrerá essa intersecção de X com A, para haver apenas o outro lado, que estamos chamando de X, e não vai ter intersecção (A+B) Por isso A (14) - x (20) = 6!
14+12+6 = 32 !!!
Pra quem está errando através do diagrama:
Uma vez colocado o número 12 como ponto comum entre SP e RJ, não se pode colocar 26 na esfera de SP, pois como está descrito no enunciado, 26 corresponde ao TOTAL DE SP, ou seja, somente SP + o valor em comum com RJ. Logo, qual valor que somado com 12 resulta em 26? 14... então 14 somente SP e 12 SP e RJ, leia novamente o enunciado na parte do 26 e olhe o diagrama novamente, 14+12= 26....
''20 escolheram apenas um dos dois estados'' ( somente SP + somente RJ = 20 ), agora matamos somente RJ, se já temos 14 apenas em SP, qual número que somado com 14 resulta em 20? 6. Agora só somar os 3 valores dentro do seu diagrama.
Dados do enunciado...
SP = 26
RJ = ?
SP e RJ = 12
Se na intersecção de SP e RJ temos 12 então podemos dizer que os que escolheram SOMENTE SP é 14.
Outro ponto importante > Se 20 escolheram APENAS UM dos dois estados e já sabemos que 14 escolheram SP então 6 escolheram SOMENTE RJ.
Ficando > Somente SP 14 + SP e RJ 12 + Somente RJ 6 = 32 candidatos
Numa cidade existem três jornais, denominados aqui por B e C. Uma pesquisa de mercado sobre os ledores desses jornais produziu os seguintes resultados: • 115 compravam o jornal A. • 208 compravam o jornal B. • 182 compravam o jornal C. • 30 compravam os jornais A e B. • 51 compravam os jornais B e C. • 30 compravam os jornais A e C. • 10 compram os jornais A, B e C. • 200 não compram nenhum dos três jornais, Com base nestas informações, assinale a opção incorreta:
Utilizar o mesmo método da questão abaixo :
2 • Q355639 [img src="http://www.questoesdeconcursos.com.br/images/icon-printer.png" alt="Imprimir"> Em uma entrevista para saber se as pessoas utilizariam os produtos A, B ou C, chegou-se a seguinte conclusão: 229 pessoas utilizariam o produto A, 223 utilizariam o produto B, 196 utilizariam o produto C, 79 utilizariam os produtos A e B, 89 os produtos A e C, 69 os produtos B e C, 37 os três produtos e 53 nenhum dos três. Nessas condições, é correto afirmar que:
Prova: IBFC - 2013 - SEPLAG-MG - Pedagogia
"Numa cidade existem três jornais, denominados aqui por A, B e C."
Além desse pequeno deslize, acredito que o examinador quis perguntar para assinalar a opção CORRETA e não a incorreta.
Sendo assim, o gabarito seria a letra B, acredito eu.
Uma entrevista foi realizada com 46 empregados de uma empresa, entre os quais 24 eram do sexo masculino e 22, do feminino. Com base nessas informações, julgue os itens seguintes.
Considerando que os empregados entrevistados dessa empresa pratiquem tênis ou ciclismo e que, na entrevista, tenha sido constatado que 30 funcionários gostam de praticar tênis e 28 gostam de ciclismo, é correto afirmar que a quantidade de empregados dessa empresa que gostam de praticar tênis e ciclismo é maior que 10.

Regra AuB = A + B - A ^ B
30 TENIS/28 CICLISMO/X=DOIS/Y=NENHUM/46=TOTAL DE 24+22
46=Y+X+30+X+28+X
46-30-28=Y-X
12=-Y+X
12+Y=X
SE Y =0 NINGUEM GOSTA DE NADA
12=X PESSOAS QUE GOSTAM DAS DUAS OPCOES
Não entendo por que está certo. 12>10 ok, mas 11>10 e com isso não atenderia os 12.
Fui pela mesma lógica da colega Mariana!!! Háaaa!
Depois que li em um comentário sobre o "Princípio da Casa dos Pombos" dei uma pesquisada e nunca mais errei questões desse tipo.
Fica a dica pra quem está começando e tem dificuldade em conjuntos, me ajudou bastante.
ELE QUER A INTERCEÇÃO PARA ACHAR BASTA SOMAR OS FUNCIONARIOS QUE GOSTÃO DAS ATIVIDADES 30+28= 58 E DEPOIS DIMINUIR COM O TOTAL DE FUNCIONARIOS QUE E O (UNIVERSO 46 ) . QUE DA 58-46= 12
30-x+x+28-x=46
58-x=46
-x=46-58
-x=-12 . (-1)
x=12
Questão correta!
Somar os conjuntos T=30 + C= 28 ,portanto, temos 58.
Agora, subtraia do conjunto universo,ou seja, 46, então temos 58-46 que é igual a 12
Agora pergunto, 12 é maior que 10 ?, sim é claro.
Gab: certo.
n(AuB) = n(A) + n(B) - n(A^B)
46(Total) = 30(Tênis) + 28(Ciclismo) - x(Valor da Intersecção)
46 = 58 - x
- 12 = - x (Multiplica por -1)
x = 12
(Gabarito Certo)
Total de empregados 46
total dos que gostam só de tênis 46 - 30 = 16 dos que gostam apenas de tênis
total dos que gostam só de ciclismo 46 - 28 = 18 dos que gostam apenas de ciclismo
dos que gostam de ambas a modalidades, soma os que gostam apenas de um esporte 18+16= 34
46 - 34, vai dar o resultado dos que gostam das duas modalidades juntas de esporte que é 12.
Bem passo a passo !!
Vamos que vamos!!!
X = CORRESPONDE A INTERSEÇÃO ENTRE A TÊNIS E CICLISMO =a quantidade de empregados dessa empresa que gostam de praticar tênis e ciclismo
TÊNIS = 30 - X
CICLISMO = 28 - X
INTERSEÇÃO = X
SOMA-SE TUDO E TEM QUE RESULTAR EM 46 (=46 empregados de uma empresa)
30-X +28-X +X = 46
58-X = 46
X = 58-46
X = 12 -->a quantidade de empregados dessa empresa que gostam de praticar tênis e ciclismo é maior que 10. CORRETA
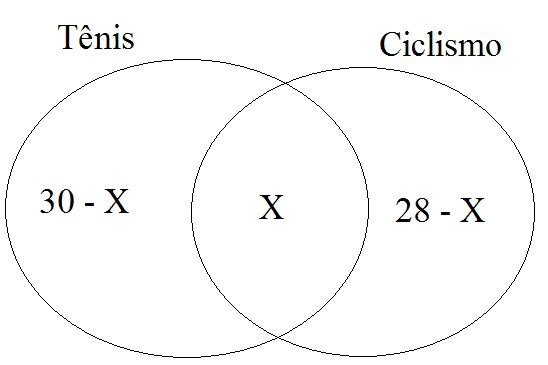 Resolvendo:
Resolvendo:30 + 28 = 58 - 46 =12 > 10
CORRETO
Não precisa de fazer todo o esquema do diagrama de venn, é só somar 30+28=58-46= 12 é maior que 10
Apenas subtraia 58 (30+28) - 46 (total da questão) = 12. 30 - 12 = 18. 28 - 12 = 16. Some tudo para confirmar: 12 + 18 + 16 = 46. Gabarito: Certo.
Jurava que teria uma intersecção com transgeneros kkkkkkkkkkkk
46= (30-x) + x + (28-x) = 12
A questão quer saber quanto vale o intersecção (tênis E ciclismo)
Forma rápida de resolver:
30+28=58
Subtrai dessa soma o valor total de funcionários: 58-46=12
12 > 10 gabarito certo.
Não precisa de uma equação pra achar esse valor, basta somar tudo e subtrair o total, o que sobrar é a interseção. O QC precisa tirar esse PHD de boteco dos comentários de professor.
46-30= 16 //// 46-28= 18 ------- soma-se : 18+16= 34, depois pegamos o total de funcionários 46-34= 12.
Gabarito CORRETO
Gabarito:Certo
Principais Dicas:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
CERTO!
http://sketchtoy.com/69858412
Selecionando- se aleatoriamente um dos veículos parados na blitz, a probabilidade de ser escolhido um em que o motorista estivesse sem documento de habilitação para dirigir seria inferior a 25%.
Resposta: ERRADO
45 (sem documento de habilitação para dirigir)
150 (Total de veículos parados)
P(E) = Número de situações favoráveis/número total de possibilidades
45/150 = 0,3 = 30% > 25%
45/150 = 0,3 = 30%
150 ----- 100%
45 ------- x
150x = 100.45
150x= 4500
x = 4500/150
x = 30% > 25%
ERRADO!
Total = 150
Extintor + habilitação = 90
habilitação = 45
Extintor= 60
45/150 = 30% gabarito errado
A questão busca confundir aquele que esboçou os conjuntos. Ao concluir os conjuntos, encontrará o valor para aqueles que não possuem CNH, de 45; e 30, para SOMENTE aqueles que não possuem CNH.
Como proceder?
O enunciado d questão não restringiu o escopo, não usou os termos "somente/apenas...". Portanto, usa-se o valor cheio.
O número de veículos que não apresentaram as irregularidades mencionadas foi superior a 50.
Resposta: CERTO
*Total de veículos parados: 150
*Total de veículos em pelo menos uma dessas duas situações: 90
150 - 90 = 60 veículos não apresentaram as irreguaridades
total - extintor sem validade: 60
total - sem CNH: 45
60+45=105
Pelo meno uma = 90, então o excesso (15) é as 2 infrações ai: 60-15 = 45 (extintor) 45-15 = 30 (sem CNH)
SOMA: 45+30+15 = 90 ------- 150-90 = 60 (não estao em nenhuma das 2 infrações
Essa foi "digrátis", da até medo de marcar de tão lógica.
Circulo 1: 45
Intersecção: 15
Circulo 2: 30
-------------------------
Total: 90
Blitz: 150-90 = 60
Olá turma, tudo bem com vcs?
Por aqui Prof. Agrelli de Academia da Matemática. Essa questão caiu em um dos simulados que respondi em meu canal. Para facilitar, veja nos comentários do link qual o número da questão que busca.
https://youtu.be/cWvICBtteqc
Espero estar ajudando em sua Jornada.
PELO MENOU UM = UNIÃO DOS CONJUNTOS
Errei uma vez para nunca mais errar.
Diagrama: http://sketchtoy.com/70233147
O número de veículos flagrados simultaneamente nas duas situações foi inferior a 20.
EXPLICACAO RETIRADA DE http://www.soensino.com.br/foruns/viewtopic.php?f=5&t=28907
O universo considerado é 150. Chamemos de E o conjunto dos 60 motoristas flagrados com extintor de incêndio com data de validade vencida e de H os 45 sem o documento de habilitação. Quando o examinador diz que o total de veículos com pelo menos uma dessas duas irregularidades observadas foi de 90, significa queE U H = 90. Utilizemos o símbolo # para representar o número de elementos (cardinalidade) de determinado conjunto. Das noções elementares de conjunto, sabemos que #(E U H) = # E + # H - #(E∩H) => 90 = 60 + 45 - #(E∩H = > #(E∩H) = 15. Assim, já possuimos elementos para respondermos os dois itens:
o número de veículos que não apresentaram as irregularidades é igual ao número de veículos abordados (150) menos o total de veículos irregulares: 90 = > 150 – 90 = 60. E o número de veículos flagrados simultaneamente nas duas situações é dado pelo valor de #(E∩H) = 15. Portanto, as respostas de ambos os itens sãocorretas.
CORRETA!
60+45 = 105
105-90= 15
A intersecção é 5, nesse caso, de fato, o número de veículos flagrados simultaneamente nas duas situações foi inferior a 20.
Foram 150 veículos parados na blitz.
90 se encaixaram em pelo menos uma das situações narradas no enunciado. Sendo assim, de um universo de 150 veículos, 60 não se encaixaram em nenhuma das situações.
Dos 90 que se encaixaram (60 com extintor vencido e 45 sem habilitação = 105. 105 - 90 = 15.
Intersecção= 15.
Excelente questão.
90 é o valor montante a ser considerado para fins de cálculo.
Diagrama: http://sketchtoy.com/70233147
Dados os conjuntos A e B , sabe-se que: A = {1;4} , B ∩ e A = {4} e A ∪ B = {1; 2; 3; 4; 5} .
Portanto, o conjunto B contém exatamente:
Se o conjunto A={1,4} e A ∪ B={1; 2; 3; 4; 5} e a intersecção é apenas um elemento comum, ou seja o elemento de nº 4, concluimos que o conjunto B não possui o apenas o nº 1, que é elemento exclusivo do conjunto A, portanto, excluindo o elemento do conjunto A da reunião entre AUB, teremos 04 elementos.
caí na casca de banana também :(
Em uma escola de informática, tem-se como o dia menos movimentado a segunda-feira, no qual estão disponíveis apenas 2 cursos: informática e digitação. O número de alunos que fazem apenas aula de informática é igual a 3x - 22 e os que fazem apenas digitação é igual a 2x + 2. Sabendo-se que o número de alunos que fazem os 2 cursos é igual a 8 e, ao todo, são 48 alunos neste dia, então, o número de alunos que fazem digitação é:

preciso de explicação :-(
mas fiz assim: Seg. 2 cursos; Inf. e Dig. 48 alunosCara... alguém mostra o desenvolvimento da conta pra mim pq eu não consigo chegar a 12 nunca!!!
Galera, depois de quebrar a cabeça aqui, eu consegui fazer essa danada. Não se trata de uma questão muito difícil, na minha opinião. Ela apenas requer atenção em sua resolução! Vamos lá.
Primeiramente é preciso consertar o enunciado. Pela prova, o número de alunos que fazem apenas aula de informática é igual a 3x-22. Já o número de alunos que fazem apenas aula de digitação está correto: 2x+2. Temos ainda o número de alunos que fazem as 2 aulas, que é 8.
O total de alunos é 48. Sendo assim temos a seguinte equação:
3x-22 + 8 + 2x+2 = 48
5x -12 = 48
5x = 60
x = 12
Após acharmos o x, devemos substituí-lo nas equações citadas no enunciado. Como a questão pede o número de alunos que fazem apenas aula de digitação, devemos somar 2x+2 + 8 para obter o gabarito. Sendo assim, temos:
2(12) + 2 + 8 = 34
Gabarito: letra c)
Abraço a todos e bons estudos!
Alguém poderia me esclarecer quando eu diminuo a intersecção do valor total de cada conjunto e quando isso nao ocorre? :/
Só não entendi o motivo para somar o + 8 em "2(12) + 2 + 8 = 34".
Adilson, 8 é o numero de alunos que fazem os dois cursos (informatica e digitação). Como a questão pede o numero de alunos que fazem o curso de digitação (total) tem que se adicionar os 8 alunos que fazem os dois cursos aos 26 (2X12+2) que fazem apenas digitação.
Espero ter ajudado.
Informática:
I = 3x - 22 (i)
Digitação
D = 2x +2 (ii)
I + D = 48-8
(2x -22) + (2x +2) = 40
3x + 2x - 22 + 2 = 40
5x -20 = 40
5x =60
x = 12
Substituindo x em i e ii temos:
I = 3x -22 D = 2x + 2
I = 3*12 - 22 D = 2*12 + 2
I = 14 D = 26
D = 26 + 8
D = 34
letra c
Entendi o seguinte de 2x+2 é que x é o total e ele fala de duas partes então 48 ÷ 2 = 24 , 24+2 =26, 26 + 8 que estuda nos dois cursos fica 34
Letra c - 34
ALTERNATIVA C)
No comentário do Filipe Rodrigues há um pequeno erro quando ele afirma na parte final que a questão pede o número de alunos que fazem apenas aula de digitação. Na realidade, a questão pede os alunos que fazem aula de digitação, por isso somamos a interseção (8) e o resultado encontrado (26). Existe uma diferença crucial em relação a isso, pois se o comando da questão tivesse mesmo pedido apenas os alunos de digitação o resultado seria 26. No mais, o resto está tudo certinho e bem explicado.
Um grupo de estudantes de Ensino Médio visitou a Biblioteca para pesquisar sobre Literatura Brasileira (LB) e Literatura Estrangeira (LE). A respeito dessa atividade, sabe- se que:
• cada estudante consultou somente uma obra;
• 40% do número total de estudantes eram meninos;
• 80% do número total de estudantes consultou obras de LB;
• 50% do total de estudantes que consultou obras de LE eram meninos;
• 20 meninas consultaram obras de LE.
Nessas circunstâncias, o número de meninas que compareceram à Biblioteca para pesquisar sobre Literatura foi de
literatura estrangeira=40 alunos e 20%
literatura brasileira= 80%
faz regra de três= 160 alunos
soma total=200 alunos
faz regra de três novamente
60% de 200= 120 meninas
Seja A o conjunto formado pelos números racio- nais maiores que –1 e menores do que 1. Seja B o conjunto formado pelos elementos de A que não são números inteiros. Então:
Gab: E
Lembrando q racionais são uma infinidade de números com vírgula, nesse caso todos compreendidos entre (-1 e 1).
Naturais = ( 0 ,1, 2, 3)
Zahl (Numeros) Inteiros = (-2, -1, 0, 1, 2)
Quociente, Racionais = (-1,99, 0,99, 0, 1,5, 2,5)
Irracionais= números infinitos
Reais = Todos menos os Complexos
Complexo = Raiz de número negativo
Li números inteiros. A pressa F%#$ tudo!
A respeito das auditorias realizadas pelos auditores A1, A2 e A3 de um tribunal de contas, concluiu-se que:
• A1 realizou 70 auditorias;
• A3 realizou 75 auditorias;
• A1 e A3 realizaram, juntos, 55 auditorias;
• A2 e A3 realizaram, juntos, 30 auditorias;
• A1 e A2 realizaram, juntos, 20 auditorias;
• das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2;
• A1, A2 e A3 realizaram, juntos, 15 auditorias.
Com base nessas informações, julgue os itens a seguir.
Mais de 100 auditorias foram realizadas.
Obrigada, Ricardo Machado, pelo link. Muito útil!
Fazendo o diagrama de Venn de acordo com os dados do enunciado:
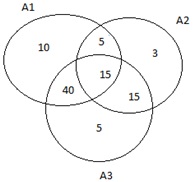
Somando
todos os valores chegamos a 93.
Errado.
e pq o 5 de A3 não entrou?
Foram realizadas 93 auditorias.
como chegaram ao 3 de A2?
Ricardo Machado, o link ajuda na matéria, mas não é a resolução da questão, que pena! Também fiquei com a mesma dúvida da Tatiana Lopes.
Continuo sem entender o porquê de subtrair 18 de 15. Ok, entendi que esses 15 é a interseção das três auditorias e deve-se retirar de A2 tudo que A1 participa, nesse caso está retirando apenas a participação das três auditorias ao mesmo tempo e as auditorias que foram feitas somente entre A1 e A2 , não deveriam ser subtraídas também? Afinal é uma auditoria diferente da que foi feita pelos três ao mesmo tempo .
Alguém pode ajudar ?
Primeiro resolva fazendo os conjuntos. Assim vai ajudar a entender.
Segundo, eu pergunto: só A2 realizou quantas? 18. Coloque nos conjuntos para entender melhor e veja que os 15 da interseçao é referente à apenas o que A2 quanto A3 realizaram juntas!!
...mas a questão diz que só A2 realizou 18. (os 5
tem o que haver c A2? Ele está no A3 sozinha!!)
Sendo A2= X+15(q ela tbm realizou)=18
A2=X= 3 (diferença entre 18 e 15)
Logo, teremos:
10+5+15+40+3+15+5=93
Estuda, estuda que Deus ajuda!
Espero eu tbm ter ajudado.
esse professor QC passa do limite da zueira. Pqp, que inútil!
Vamos lá: Se vc tem dúvida em porque 18 - 15 = 3
Entenda que na questão enunciada é dito : das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2
A1 sozinho = 10
A1, A2 e A3= 15
A1 e A3 = 40
A1 e A2 = 5
A3 e A2 = 15 Portanto o único valor que temos fora do conjunto A1 é 15 / logo 15 (auditorias que não foram realizadas por A1) - 18 (auditorias que não foram realizadas por A1) = 3
Espero ter ajudado.
Fiz um vídeo bem pequeno, apenas a parte de como chegar no resultado das auditorias feitas apenas por A2,
espero que seja útil.
https://youtu.be/NvgZruJ8gPE
a duvida pra mim é seguinte: " ele diz das auditorias q n foram realizadas por A1.
a3 e a2 = 15 n foram realizadas por A1
agora os 5 q somente estao em A3 tbm n foram realizadas por A1 correto. entao pq n entra na soma.
muitos estão em /duvida da onde veio o bendito numero 3 da conta. Vou tentar explicar!
Vamos por partes:
Quando a questão diz que das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2. Ela esta me dando o total de auditorias que apenas A2 realizou sozinho e dizendo para desconsiderar o A1 no calculo, Logo:
A1 realizou 70 auditorias
A2 realizou 38 auditorias
A3 realizou 75 auditorias
A1 e A3 realizaram 55 auditorias
A2 e A3 realizaram 30 auditorias
A1 e A2 realizaram 20 auditorias
A1, A2 e A3 realizaram juntos 15 auditorias
Se A2 e A3 realizaram juntos 30 auditorias e sabendo que A1,A2 e A3 realizaram juntos 15 auditorias. (30 - 15 = 15)
Se A1 e A2 realizaram juntos 20 auditorias e sabendo que A1,A2 e A3 realizaram juntos 15 auditorias. (20 - 15 = 5)
A1,A2 e A3 realizaram juntos 15 auditorias.
Portanto se eu sei que das 18 auditorias A2 fez sozinho. E que juntos A2 e A3 já fizeram 15 e o A1 não entra na conta logo (18 - 15 = 3).
15 + 5 + 15 +3 = 38 Total do conjunto A2
GABARITO ERRADO
somando todos os conjuntos o total de auditorias realizadas é igual a 93.
Espero ter ajudado, Bons estudos galera!
Para quem não entendeu, olhem o finalzinho da questão nessa explicação do Gilberto Wrignt: https://youtu.be/NvgZruJ8gPE
Faça um diagrama com três bolas. Na primeira coloque A1, na segunda coloque A2 e na terceira coloque A3.
Na interseção entre as três coloque o valor de 15.
A1 e a A3 realizaram 55 auditorias. Na interseção entre A1 e A3 coloque o valor de 40. (55-15 da interseção)
A2 e a A3 realizaram 30 auditorias. Na interseção entre A2 e A3 coloque o valor de 15. (30-15 da interseção)
A1 e a A2 realizaram 20 auditorias. Na interseção entre A1 e A2 coloque o valor de 5. (20-5 da interseção)
A1 = 70 auditorias. Observando os valores dentro da bola de A1 temos: (40+15+5=60). Para dar 70 falta 10. 10 corresponde as auditorias feitas apenas por A1.
A3= 75 auditorias. Observando os valores dentro da bola de A3 temos: (15+15+40=70). Para dar 75 falta 5. 5 corresponde as auditorias feitas apenas por A3.
Fazendo pelo diagrama fica mais fácil de se visualizar a questão.
A questão ainda diz que "Das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2". Devemos desconsiderar todos os valores que envolvem A1 (10,5,15,40). Na bola A3 observa-se que sobrou o valor de 5 que corresponde as auditorias feitas apenas por A3 e sobrou o valor de 15 (interseção entre A2 e A3). Como em A2 foram realizadas 18 auditorias, (18-15=3).
Somando tudo temos o total de 93 auditorias.
Ou seja a questão está errada, pois 93 < 100.
Soma: 55+30+20+15= 120- 30= 90+3 = 93 auditorias
Temos 5 aud feita por A3, 10 por A1 e 15 por A2. Somados dão 30
Como tbm • das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2;
18-15= 3
Gaba: ERRADO
fiz um vídeo que explica como achar o A2
https://youtu.be/JVXP2exL82Y
o vídeo do colega não esta mais no ar.
bons estudos.
A respeito das auditorias realizadas pelos auditores A1, A2 e A3 de um tribunal de contas, concluiu-se que:
• A1 realizou 70 auditorias;
• A3 realizou 75 auditorias;
• A1 e A3 realizaram, juntos, 55 auditorias;
• A2 e A3 realizaram, juntos, 30 auditorias;
• A1 e A2 realizaram, juntos, 20 auditorias;
• das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2;
• A1, A2 e A3 realizaram, juntos, 15 auditorias.
Com base nessas informações, julgue os itens a seguir.
20 auditorias foram realizadas apenas por A1.
Primeira parte
A1, A2 e A3 realizaram, juntos, 15 auditorias.
Segunda parte
• A1 e A3 realizaram, juntos, 55 auditorias; (55– 15= 40)
• A2 e A3 realizaram, juntos, 30 auditorias; (30-15 = 15)
•A1 e A2 realizaram, juntos, 20 auditorias; (20 -15= 5)
Terceira parte
A1 realizou 70 auditorias; (70 – 15 -40 – 5= 10)
• A3 realizou 75 auditorias; (75 – 15 -15 -40 = 5)
Quarta parte
• das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2; (18 – 15= 3)
OBS: A1 não participa (tudo com A1 não entra ).
2. 20 auditorias foram realizadas apenas por A1.
Resposta: errada
70 – 15 -40 – 5= 10
Fiz as 3 questões por conjunto conforme foi comentado pela amiga, mas não consegui colocar no comentá.
Posso mandar por e-mail se alguem desejar.
ste comen
Fazendo o diagrama de Venn:

Assim
fica fácil ver que o auditor A1 fez apenas 10 auditorias e não 20.
Errado.
Print do Diagrama: http://prntscr.com/7scgg1
Fiz um vídeo bem pequeno, apenas a parte de como chegar no resultado das auditorias feitas apenas por A2,
espero que seja útil.
https://youtu.be/NvgZruJ8gPE
Apenas 10!
FOCOFORÇAFÉ#@
ÓTIMO VÍDEO GILBERTO WRIGNT.
Gaba: ERRADO
fiz um vídeo que explica como achar o A2
https://youtu.be/JVXP2exL82Y
o vídeo do colega nao esta mais abrindo.
bons estudos.
A respeito das auditorias realizadas pelos auditores A1, A2 e A3 de um tribunal de contas, concluiu-se que:
• A1 realizou 70 auditorias; • A3 realizou 75 auditorias;
• A1 e A3 realizaram, juntos, 55 auditorias;
• A2 e A3 realizaram, juntos, 30 auditorias;
• A1 e A2 realizaram, juntos, 20 auditorias;
• das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2;
• A1, A2 e A3 realizaram, juntos, 15 auditorias.
Com base nessas informações, julgue os itens a seguir.
23 auditorias não foram realizadas por A1.
Primeira parte
A1, A2 e A3 realizaram, juntos, 15 auditorias.
Segunda parte
• A1 e A3 realizaram, juntos, 55 auditorias; (55– 15= 40)
• A2 e A3 realizaram, juntos, 30 auditorias; (30-15 = 15)
•A1 e A2 realizaram, juntos, 20 auditorias; (20 -15= 5)
Terceira parte
A1 realizou 70 auditorias; (70 – 15 -40 – 5= 10)
• A3 realizou 75 auditorias; (75 – 15 -15 -40 = 5)
Quarta parte
• das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2; (18 – 15= 3)
OBS: A1 não participa (tudo com A1 não entra ).
1. Mais de 100 auditores foram realizadas
Resposta: errada
15+40+10+5+3+15+5= 93
2. 20 auditorias foram realizadas apenas por A1.
Resposta: errada
70 – 15 -40 – 5= 10
3. 23 auditorias não foram realizadas por A1.
Resposta: certa
3+5+15=23
A1, A2 e A3 realizaram, juntos, 15 auditorias.
das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2; (18 – 15= 3)
A2 e A3 realizaram, juntos, 30 auditorias; (30-15 = 15)
A3 realizou 75 auditorias; (75 – 15 -15 -40 = 5)
Fazendo o diagrama de Venn:

Fazendo a
soma das auditorias que não envolvem o auditor A1: 5+15+3 = 23.
Certo.
Alguém pode me ajudar? Ainda não consegui chegar no cálculo do A2 ...
Não entendi pq as 5 do A3 não entra no cálculo para diminuir as 18 auditorias não feitas pelo A2. (???)
O comentário da Elane ajuda bastante. Obrigada!
Fiz um vídeo bem pequeno, apenas a parte de como chegar no resultado das auditorias feitas apenas por A2,
espero que seja útil.
https://youtu.be/NvgZruJ8gPE
23 auditorias não foram realizadas por A1.
Cara,se não foi A1 que realizou quem poderia ser? A2 e A3(tem que levar em conta o número que os dois fizeram juntos também)
tampa a quantidade de A1...o que resta é 5 + 15 + 3 = 23...realmente 23 não foram realizadas por A1...Bons estudos
Valeu Gilberto Wright, só entendi a questão depois que assisti seu vídeo.
Parabéns pela ótima contribuiçao, deve ter ajudado muitas pessoas pq tem mais de 900 visualizações.
Gaba: CERTO
fiz um vídeo que explica como achar o A2
https://youtu.be/JVXP2exL82Y
o vídeo do colega não esta mais no ar.
bons estudos.
O que faz gerar duvidas é a palavra SOMENTE, que é diferente de APENAS.
Gabarito:Certo
Principais Dicas:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
CERTO!
http://sketchtoy.com/69841180
(apenas)B= 150 (apenas)D = 120 (apenas)E= 180
BD = 40 DE = 30 BE = ? BDE=?
CONTA 1:
utilizados 260 comprimidos de vitamina B e 210
comprimidos de vitamina D
Total de D= 210
Total de B= 260
TD = 120 + 40 +30 + BDE
210 = BDE + 190
BDE = 210 – 190 = 20
CONTA2:
TB = 150 + 40 + 20 + BE
260 = 210 + BE
BE = 260 – 210
BE = 50
Sendo assim o número de participantes que
tomam exatamente 1 comprimido de vitamina B
e 1 comprimido de vitamina E diariamente é 50
Então resposta letra A
A pergunta foi a quantidade de participantes do grupo BE.
A soma dos participantes dos grupos informados pelo enunciado são (B150) + (D120) + (E180) + (DE30) + (BD40) = 520 participantes. Mas o enunciado informou que a quantidade total eram de 590 participantes, ou seja, faltam 70 que não foram informados.
Foi informado no enunciado que diariamente são utilizados 260 comprimidos de vitamina B, mas a soma (B150)+(BD40)=190 comprimidos B, ou seja, faltam 70 comprimidos, portanto dos 70 participantes não informados todos tomam 1 comprimido de vitamina B.
São utilizados diariamente 210 comprimidos de vitamina D, mas a soma (D120)+(DE30)+(BD40)=190 comprimidos D, ou seja, faltam 20 comprimidos D, portanto 20 participantes dos 70 não informados tomam vitamina D.
Conclui que apenas 50 participantes tomam vitamina B e E.
Uma pesquisa realizada com um grupo de 35 técnicos do MPU a respeito da atividade I - planejamento estratégico institucional - e da atividade II - realizar estudos, pesquisas e levantamento de dados - revelou que 29 gostam da atividade I e 28 gostam da atividade II. Com base nessas informações, julgue os itens que se seguem.
A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7.
Cespe sempre quebrando as pernas de quem sabe...
Li a questão e já imaginei que era inferior a 6 e não 7. Só que 6 é inferior a 7...
Acho que essa é a única banca que derruba os candidatos de todas as formas possíveis.
Alguem poderia me explicar porque tem que se adotoar o maio valor de x pra se conseguir o maior valor de y?
Eu até entendo que o maior de x é 28 porque não se pode ter um numero negativo de pessoas num dos grupos, mas porque isso leva ao maior valor de y?
total de técnicos 35
só gostam da atividade I = 29 - x
só gostam da atividade II = 28 - x
gostam das duas atividades = x
não gostam da duas atividades = y
logo, o total fica 29 - x + 28 - x + x +y = 35
calcula x - y = 22
agora começa a atribuir valores a y:
x-1=22 ...x=23
.
.
x-7=22 ...x=29
vc tem que perceber que qd x= 29 os que gostam da atividade I fica = 0 e os que gostam da atividade II ficará negativo
ver retomando o inicio da questao
só gostam da atividade II - 28 - x, troca o x por 29 dá igual a -1impossível. Tem que ser menor que 7.
Galera vem sempre com calculos mirabolantes. Mas lembrem-se: O CESPE FAZ ISSO PRA CANSAR O CANDIDATO! Tem SEMPRE uma maneira simples de resolver, SEMPRE! Concordo com o Luis Pereira!
Sinceramente, não vi ninguém, até agora, explicando a questão de forma lógica. Nada realmente objetivo.
35 é o total de técnicos.
29 gostam da atividade I
28 gostam da atividade II
Suponha que todos da atividade II gostem da atividade I
28 que gostam das duas atividades + 1 que gosta somente da atividade I = 29 gostam de alguma atividade
total de tecnicos - tecnicos que gostam de alguma das atividades = nao gostam de nenhuma atividade
35-29=6
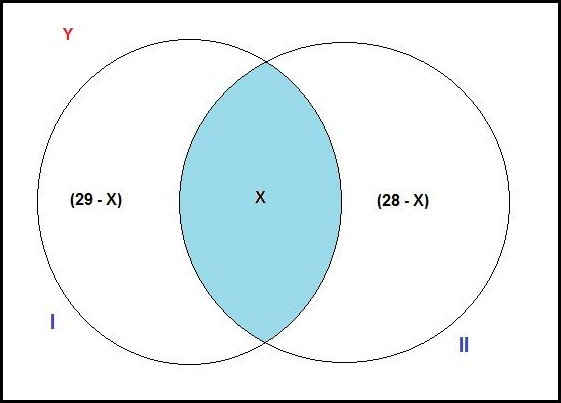
OI PESSOAL, ALGUÉM SABE FAZER ESSA QUESTÃO ATRAVÉS DE DIAGRAMA?
ABRAÇOS ZENAIDE. PERNAMBUCANA, O FREVO COMENDO E EU ESTUDANDO RACIOCINIO LÓGICO. KKKKKKKK.
GABARITO CORRETO
35 entrevistados; 29 atividade1; 28 atividade2
a interseção tem que ser 22 que gostam das das duas atividades, pois tem-se 35 candidatos. até aí beleza!
agora quantos gostam exclusivamente; atividade 1= 29-22=7; atividade 2=28-22=6
a questão tá afirmando que a quantidade máxima de técnicos que se pode ter para não gostar de nenhuma das atividades é inferior a 7.
tem que ser pois se O máximo que se tem de membros gostando só de uma atividade são 7 membros da atividade 1, se for igual a 7 ou maior então se terá um conjunto vazio, porque se não gosta de um não tem jeito de gostar dos dois. em outra palavras:
se 6 pessoas não gostarem da atividade 2, ela esvaziará, mas ainda restará 1 da atividade 1.
Olá pessoal!
Bem, entendi da seguinte forma:
A questão afirma que a quantidade máxima de pessoas que não gosta de nenhuma das atividades é inferior a 7.
Vamos la
O universo é 35
U = 35
Os que gostam da atividade 1 é igual a 29
Os que gostam da atividade 2 é igual a 28
A soma de 28 + 29 será maior que meu universo, logo existem técnicos que gostam de ambas as atividades.
Vamos encontrá-los:
29 + 28 = 57
57 - 35 = 22 (estes são os que gostam de ambas as atividades)
Quem gosta somente da atividade I?
29 - 22 = 7 (técnicos que gostam somente da atividade I)
Quem gosta somente da atividade II?
28 - 22 = 6 (técnicos que gostam somente da atividade II.
Resolução:
Temos então que 22 gostam de ambas, 7 gostam da atividade I, 6 gostam da atividade II. Com isto temo o total do nosso Universo, ou seja, igual a 35. Logo temos o conjunto dos que não gostam de nenhuma das atividades como vazio, isto é, zero. Assim zero é menor do que 7.
Eu raciocinei da mesma forma que o Jansen
Gostaria de ajudar com o diagrama de Venn, mas nao consigo inserir figuras aqui.
Façam o seguinte: coloquem um círculo um dentro do outro, o de dentro chama de II e o de fora de I, ou seja 28 técnicos que gostam de II gostam também de I, mas no enunciado ele diz que 29 técnicos gostam de I então está faltando apenas 1, ou seja apenas um técnico gosta APENAS da atividade I, somando 28+1=29 como foram entrevistados 35 faça um círculo separado e coloque o numero 6 ou seja: 6 técnicos não gostam de nenhuma das atividades. 29+6=35. Faça os círculos, fica super fácil de entender.
Força Foco e Fé!!!
OLHA EU PENSEI ASSIM: CONSIDEREI A RESPOSTA DO ENUNCIADO COMO CORRETA, PORTANTO
28+29+7-X (INTERJEIÇÃO) = 35, TODAVIA TENDO COMO RESPOSTA 29, O QUE NÃO PODERIA OCORRER,
SENÃO TERÍAMOS UMA RESPOSTA NEGATIVA, LOGO RESPOSTA ERRADA.
Tentando ajudar...
1º Passo somar todo mundo e utiliza o 7 dado pela questão. Ele será o parâmetro da nossa resposta. E o que procuraremos? A intercessão!
29-x+x+28-x+7=35
64-x=35
-x-29
x=29
Achamos X=29. Como X é a intercessão, percebe-se que há algo de estranho. Como fica a atividade II? 28(atividade II) - 29(intercessão)= -1. Isso pode? Não!
E, se colocarmos 6 no lugar de 7? Ai sim. E como 6 <7. A resposta é CERTA.
Treine com exaustão até a perfeição.
35 - 29 = 6
29 gostam da Atividade 1.
28 gostam da Atividade 2. Logicamente, estes 28 também curtem a Atividade 1.
OLA, VOU SER OBJETIVO PARA VOCÊ ENTENDER
NA ATIVIDADE I TEMOS 29 TÉCNICOS QUE GOSTAM DELA
35-29= 6
NA PIOR DAS HIPÓTESES TEREMOS 6 TÉCNICOS QUE NÃO GOSTAM DE NENHUMA DAS ATIVIDADES.
Pessoal, quando abrirmos a aba acima para analisarmos o comentário do professor, vamos solicitar ao QC que coloque as explicações em vídeo aulas.
JANSEN CARVALHO o único que desvendou a questão nos comentários, para os recém chegados nem percam tempo, vão direto no comentário dele que é o correto.
Galera, a formula é a seguinte para se chegar à conclusão de que não há que não goste das atividades I e II:
A U B= A+B - A^B
Os comentários desse professor de Matemática são complexos demais. Em vez dele descomplicar, ele complica... Troquem de professor, pelo amor de Deus !!
Minha dificuldade aumentou depois de olhar o comentário do professor!!!
Pelo amor de Deus Q ... assim não dá...gravem vídeos como em Português, assim fica impossível, ninguém aqui entende o que o professor diz.
Atividade: 1= 29 2=28 para achar a interseção do conjunto é só somar ativ( 1+2) e pegar o conjunto universo, ou seja, 35, e subtrair, agora subtraindo 57-35, pronto achamos 22.
Bom 29-22 =7 28-22= 6
agora somando 7+6+22 temos 35 que fizeram alguma atividade. Bom se o meu total é 35, e eu sei que 35 fizeram alguma atividade, então subtraindo 35-35 temos, portanto, 0, ora 0 é menor que 7 ?, kkkkkkkkkk, claro que é. então
Gab: certo.
Espero ter ajudado, detesto o jeito de explicar RLM deses professor aqui do site.
Isso, a quantidade máxima de técnicos que não gosta de nada é = a 0, ou seja, todo mundo gosta de alguma coisa!!
Equipe Q.C, ficaríamos satisfeitos se colocassem videos de resolução das questões de R.L.M / Matemática. Uma questão simples como essa acaba se tornando difícil quando lemos a explicação do Prof. por escrito. Vai a dica...
Resoluções em vídeos, pelo amor de Deus!!!!!
Em RL e algumas outras matérias, os comentários dos alunos são mais eficientes que a resposta dos professores.
QC, melhora aí!
*****Um método diferente, resolvam pela resposta.
A=ATIVIDADE I, B= ATIVIDADE II
X= Intersecção de A e B (gostam de ambas atividades)
Y= Não gostam de nenhuma das duas atividades
A= 29 - X
B= 28 - X
Sendo (29-X) + (28-X) + X + Y = 35
----------------------------------------------------------------------------------------------
hipótese 1: Y = 7 (7 veio da afirmação da questão)
(29-X) + (28-X) + X + Y = 35
(29-X) + (28-X) + X + 7 = 35
-X + 64 = 35
X = 29 . Reparem agora, que se substituíssemos aqueles que gostam apenas da atividade II, ou seja, B, teríamos:
B = 28 - X
B = 28 - 29
B = -1. Ora, não podemos ter um número negativo de pessoas que não gostam da atividade II. Portanto, Y = 7 não é possível (assim como qualquer outro nº maior que 7, faça as contas se achar que deve).
----------------------------------------------------------------------------------------------
hipótese 2: Y = 6 (n° mais próximo inferior a 7, conforme afirmação da questão)
(29-X) + (28-X) + X + Y = 35
(29-X) + (28-X) + X + 6 = 35
-X + 63 = 35
X = 28 . Reparem agora, que se substituíssemos aqueles que gostam apenas da atividade II, ou seja, B, teríamos:
B = 28 - X
B = 28 - 28
B = 0. Ora, pode acontecer que ninguém goste somente da atividade II. Portanto, Y = 6 é possível (assim como qualquer outro número menor que 6, faça as contas se achar que deve). Assim, Y < 6, ou (conforme a questão) Y < 7. Gabarito correto!
se considerarmos B com somente 28 e que todos eles se encontrem na interceção de A com B , sobra somente 1 em apenas A e sobra 0 em apenas B .
escrevam não gostei e peçam vídeo, no comentário do prof.
Mônica Sátolo, excelente raciocínio! Realmente é a única coisa que se pode afirmar com certeza.
Encontrei a resposta. Se lerem devagar dá pra entender.
É assim: tem o conjunto da atividade I e tem o conjunto da atividade II
*Se são 35 entrevistados e 29 gostam da atividade I e 28 gostam da atividade II, bom, então: 28+29 = 57 e 57-30 = 22
*Então de início temos 22 que gostaram das duas simultaneamente.
*A questão diz que: A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7.
*Então temos que tirar elementos de dentro dos conjuntos e colocar do lado de fora, representando os que não gostam de nenhuma das duas atividades.
*de inicio ficaria assim:
*I →7 I e II→22 II→6 totalizando 35
Se tirarmos 1 elemento do conjunto I e colocássemos do lado de fora, teríamos que aumentar a interseção para 23, para manter a soma(29) dos que gostaram da atividade I, e diminuir a quantidade do conjunto II para 5, para manter a soma(28) dos que gostam da atividade II, dessa forma: 6 + 23 + 5 + 1 = 35. A partir daí continuamos a aumentar o numero dos que ficaram do lado de fora, ou seja, dos que não gostam de nenhuma das atividades.
*(I →6 I e II→23 II→5) + 1 totalizando 35
*(I →5 I e II→24 II→4) + 2 totalizando 35
*(I →4 I e II→25 II→3) + 3 totalizando 35
*(I →3 I e II→26 II→2) + 4 totalizando 35
*(I →2 I e II→27 II→ 1) + 5 totalizando 35
*(I →1 I e II→28 II→0) + 6 totalizando 35 >>>> a partir daqui não se pode tirar mais nenhum elemento de dentro dos conjuntos, pois o conjunto II ficaria negativo(-1), o que não existe.
*Dessa forma o máximo de técnicos que podem não gostar de nenhuma das atividades é 6, que é inferior a 7. Portanto:
Gabarito CERTO
A partir desse meu último comentário, provo que os comentários que dizem que está certo porque os que não gostam de nenhuma atividade são 0, e 0 é menor que 7, partem de um raciocínio equivocado.
O jeito do Jasen não está correto, visto que o valor de x encontrado por ele é uma SUPOSIÇÃO, e não uma certeza. Podemos sim ter aqueles que não gostam de nenhuma das duas atividades.
Fiz da seguinte maneira:
x= intersecção
y= os que não gostam de nenhuma das duas atividades
Assim, x + 29-x + 28-x + y= 35
29 + 28-x + y= 35
-x + y= 35 - 29 - 28
-x + y = - 22 (multiplica por -1)
x - y = 22
x = 22 + y
Ora, se y for 7, x será igual a 29. Assim, se os que gostam somente da atividade I é 29 - x, teremos 29 - 29. Ou seja, nenhuma pessoa do grupo gosta apenas da atividade I. Até aí é possível, mas, ao aplicarmos aos que gostam somente da atividade II, teremos 28 - 29 = -1. O resultado negativo não é possível. Por isso, o valor é inferior a 7 (6 ou menos).
https://www.youtube.com/watch?v=R4XeRZ0f0g8
Galera achei este vídeo do professor Bruno Lima.
Ele não resolve está questão mais sim uma questão muito parecida "no momento 24 minuto do vídeo" Vocês adiantam o vídeo e vai chegar em umas resoluções muito aproveitáveis .
Espero que ajudem.
Eu só fiz o valor total que é 35 menos o valor maior da atividade II que é 29 = 6 então esta correta a acertativa...
Vamos pedir resoluções em vídeo!
Clica na explicação do profº e em seguida em Não gostei. depois justifica: quero explicações em vídeo!
Esse professor é um ogro não sabe explicar nada!!!
pela lógica da zero, logo zero é menor que 7, mas do jeito que o professor explicou fica impossível de se entender....
Josimar padilha do gran cursos on line resolve essa questão e explica muito bem
Pensei assim: o número máximo de pessoas que gostam de alguma atividade é 29 e dentro destes PODEM está os 28 que gostam da atividade II. Podemos pensar na seguinte hipótese: 28 técnicos gostam das atividades I e II e apenas 1 técnico gosta somente da atividade I, assim, cumpre-se o que a questão cita: 29 gostam da atividade I (28 + 1) e 28, da atividade II (interseção das atividades I e II). Ora, se dos 35 apenas 29 gostam de algo, no máximo 6 não gostam, logo, número inferior a 7 tornando correta a questão.
Sempre que você vir uma questão pedindo esse tipo de resolução, basta pegar o total e subtrair pelo valor do maior conjunto, sem mistério.
Obrigado pela as explicações aqui nos comentários se for depender do professor do QC tava era morto, tem uma preguiça da porra de gravar um vídeo
https://www.youtube.com/watch?v=Ia-slXgm1MA
ae galera todas do MPU TÉCNICO 2013 acabou o problema rs
Só consegui entender após ler o contário da MONICA SÁTOLO obrigado
Copiando o enunciado: A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7.
Na atividade I temos 29 pessoas; na atividade II temos 28 e no total temos 35. Se fizermos a conta achamos a intersecção que dá 22, mas isso não é necessário.
Para ter a QUANTIDADE MÁXIMA, precisamos colocar O MÍNIMO POSSÍVEL. É uma antítese, mas é bem simples. A explicação em escrito pode ficar confusa, mas tente colocar no papel que fica fácil de visualizar.
Temos Dois conjuntos: I com 29 pessoas, II com 28 pessoas e uma intersecção supostamente como x.
Coloque o menor valor (28) como se fosse a intersecção. No CONJUNTO I TOTAL continua com 29 e o CONJUNTO II TOTAL passa a ter 0.
Bom, 29 - 28 = 1 (ou seja, 29 do total do conjunto I - 28 da intersecção). Chegamos no valor MÍNIMO POSSÍVEL.
Agora é só tirar do total que temos o número que não gosta de nada, 35 - 29 = 6 ( ou seja, 35 técnicos no geral menos 29 pessoas que estão dentro do conjunto).
Espero ter ajudado.
Atividade 1 = A
Atividade 2 = B
Gostam da atividade 1 = n(A) = 29
Gostam da atividade 2 = n(B) = 28
Gostam das duas = n(A∩B)
Não gostam de nenhuma = n(Y)
Nesse tipo de questão, onde não se sabe o valor da interseção nem o valor de fora dos dois conjuntos, e a questão pede justamente esae valor de fora, deve-se buscar a pior das hipóteses. A pior hipótese é aquela em que o valor da interseção é o valor do menor conjunto, no caso da questão 28, não será 29 pois caso fosse, na hora de achar o valor dos que gostam da atividade 2 menos a interseção (28 - 29) restaria um número negativo, o que não pode ocorrer.
Então a expressao fica assim:
35 = (29-28) + 28 + (28-28) + n(Y)
35 = 29 + n(Y)
n(Y) = 6
Gabarito certo
Gente.. até dá pra resolver com cálculos, mas é mais simples por raciocínio: Se 29 já responderam que gostam da atividade I, podemos supor que os 28 que gostam da atividade II são os mesmos 29 (menos 1), pois a questão não restringe nada nesse sentido. Assim, se ao menos 29 de 35 responderam, o número máximo de abstenções possível é 35-29=6, que é inferior a 7.
Melhor do que sair escrevendo teorias, textos e mais textos... é bom procurar uma resolução que nos faça compreender. Segue abaixo um vídeo (NEAF Concursos) uma explicação rapidinha e que (pelo menos para mim) resume a explicação. E podemos levar para outras questões pois é MUITO teórica.
https://www.youtube.com/watch?v=DSVpZCMIHkc
Espero ter ajudado!
O total técnicos são de 35, e que 29 gostam da atividade I e 28 gostam da atividade II,como eu não sei o valor da intersercção vamos chama-la de X, e atribuir Y para aqueles que não gostam de nenhuma dessas atividades,ficando assim :
29- x+x+28-x+y=35
Supondo que X vale 28 realizaremos a substituição na equação
29-28+28+28-28+Y=35
1+28+Y=35
29+Y=35
Y=35-29
Y=6
CERTO
Galera, temos 29 técnicos que gostam da atividade 1, certo ?
35-29=6
Logo, só tem como 6 técnicos (no máximo) não gostarem de nenhuma atividade.
6<7
Aprendi com um professor assim; Sempre que pedir a quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades (ficar fora do diagrama) Pegar o menor valor (28) jogar na interseção (28),
e verificar quantos faltam para completar o diagrama II. Não falta nenhum, (0) pois são 28 mesmo.
Quantos faltam para completar o diagrama I, APENAS (1), POIS já há o (28), então, quantos faltam para completar 35? apenas (6). Essa é a reposta, o valor que fica fora.. Desenhando fica mais fácil...
EXPLICAÇÃO:
https://www.youtube.com/watch?v=DSVpZCMIHkc
Uma pesquisa realizada com um grupo de 35 técnicos do MPU a respeito da atividade I - planejamento estratégico institucional - e da atividade II - realizar estudos, pesquisas e levantamento de dados - revelou que 29 gostam da atividade I e 28 gostam da atividade II. Com base nessas informações, julgue os itens que se seguem.
Se 4 técnicos desse grupo não gostam de nenhuma das atividades citadas, então mais de 25 técnicos gostam das duas atividades.
Possa até falar besteira...Mas de qualquer modo não é mais que 25??
esta certo
Universo=35 Logo se soma 29+28+4=61 Subtrai 61-35=26
Eu fiz assim:
Universo: 35 / 29 gosta de I, 28 gosta de II / R=Não gosta de I e II. / G = Gosta de I e II.
G=25, temos I= G+4 e II=G+3, R=3.
G=26, temos I= G+3 e II=G+2, R=4.
G=27, temos I= G+2 e II=G+1, R=5.
G=28, temos I= G+1 e II=G+0, R=6.
Fazendo o
diagrama de Venn:
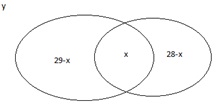
Assim temos de um total de 35 – 4 = 31
técnicos gostam de I e de II, somando-se 29 + 28 = 57 e finalmente
subtraindo-se esse valor de 31, acharemos o resultado final (intercessão)de 26
técnicos.
Resposta: Certo
OI COLEGA DE ESTUDOS, PEDRO IVO, VOCÊ CONSEGUERIA RESPONDER ESSA QUESTÃO POR DIAGRAMA, JÁ QUE ENCONTROU A INTERSECÇÃO.
ABRAÇOS, ZENAIDE.
resolvi utilizando a seguinte fórmula: n(A  B) = n(A) + n(B) - n(A
B) = n(A) + n(B) - n(A  " B)
" B)
Como 4 não gostam de nada, sobram 31 da união dos dois conjuntos (os que gostam de I e os que gostam de II). Daí coloquei os valores na fórmula:
31 = 29 + 28 - X, que resolvendo dá X=26, que é a interseção entre os dois conjuntos, ou seja, a quantidade que gosta das duas atividades.
35 - 4 = 31
28 + 29 = 57
57 - 31 = 26
Gabarito. Certo.
Atividade I -> 29
Atividade II -> 28
para achar os comuns de I e II =
29-x+28-x+4+x = 35
61 -x = 35
x = 26
Lorena, concordo que realmente os comentários dos professores normalmente não me ajudam, eu discordo quanto a esse comentário, pois a explicação foi simples e efetiva.
Não entendi o "x" do 4+x, para mim seria 29-x+28-x+4 = 35. atividade I, menos interseção, atividade II menos interseção + quem não gosta de nenhum dos 2 é igual a 35
Fiz dessa forma:
29+28+4=61
61-35=26(Que e a INTERSECÇÃO)
Total de técnicos= 35 - 4 que não gostam de nenhuma atividade = 31 29+28 = 57-31= 26
Gente, me corrijam por favor se for o caso; O que eu entendi é que a resposta é Certa e o professor resolveu a questão mas colocou Errado, ou seja, ele errou a questão...
Pessoal, enviei esta mensagem para a organização do QC. Acho que estamos desamparados pelo prof. de matemática.
comentários em vídeos por favor, estamos desamparados nos comentários do professor de matemática. Ele usa uma linguagem muito complexa, complica muito a questão e se torna incompreensível.
Se vc, assim como eu não consegue entender nada que o prof. "ESCREVE", clica lá no comentários do prof. e clica em não gostei, pra ver se conseguimos entender alguma coisa em vídeo.
Se 4 passaram a não gostar de nenhuma das atividades citadas, então a interseção muda para 26.
29 - x + x + 28 - x + 4 = 35 x = 26, logo mais de 25 gostaram das duas atividades.
Na questao anterior era apenas 29 - x + x + 28 - x = 35 x = 22
o professor disse que ta errado, kkk não sei o porque. professor Renato oliveira pra explicar em video já, o cara é show
conjunto I = 29 - x (interseção)
conjunto II = 28 - x (interseção)
interseção = x
não gostam de nenhuma das atividade = 4
total de técnicos da pesquisa =35
(29-x) +x + (28-x ) +4= 35
61-x =35
x= 61 - 35
x = 26 (resposta correta)
O jeito que fiz foi assim.Muito fácil e rápido.
Pega os numero: 29(I), 28(II), e 4(é o que ele dá na questão) e 35 que é meu Universo
Resolução: 28+29+4 = 61
61-35= 26
Tem gente aqui que acertou, mas errou nas contas.
Essa matéria necessita de vídeo aula.
SE 4 NÃO GOSTAM NEM DA 1ª E NEM DA 2ª, ENTÃO SÓ SOBRARÃO 31 DELES (35-4=31)
29+28= 57
57-31=26 (GOSTAM DA 1ª E DA 2ª)
GABARITO CERTO
Pessoal o professor está certo!!!
Veja que no final a banca faz uma pegadinha e escreve: então mais de 25 técnicos gostam das duas atividades.
Mas os técnicos Não gostam das duas atividades. Foi isso que eu entendi...
R: Certo.
Veja a correção do Professor Josimar Padilha.
https://www.youtube.com/watch?v=xY0zsyETD50&list=PLZIcuMePV18xqrIk9hOyVfRhnpLRXpqrl&index=3
Marayza Pontes acho que vc está equivocada colega.
Total de Técnicos=35
Gostam da ativ.I=29
Gostam da ativ.II=28
Não gostam de nenhuma=4
Somando tudo fica assim: 29+28+4=61
Diminui o total de técnicos: 61-35=26 (29-26=3 / 28-26=2)
26 são os que gostam das duas atividades
4 são os que nao gostam de nenhuma
3 são os que gostam apenas da ativ.I
2 são os que gostam apenas da ativ.II
Resolvi pelo Diagrama.
Colocar as duas bolas. A primeira indicando as pessoas que gostam da atividade I. A segunda indicando as pessoas que gostam da atividade II. Na primeira o valor é 29-x (x porque não conhecemos o valor da interseção). Na segunda bola colocamos o valor de 28-x. Na interseção colocamos o calor de x.
Sendo assim temos: 29-x+x+28-x+4=35
Resultando em 26.
*4 se refere ao número de pessoas que não gostam de nenhuma das atividades.
A QUESTÃO ESTÁ CORRETA. MAIS DE 25 TÉCNICOS GOSTAM DAS DUAS ATIVIDADES.
ATIVIDADE I = 29
ATIVIDADE II = 28
29 - 2 = 27
28 - 2 = 26
SENDO ASSIM, MAIS DE 25 TÉCNICOS GOSTAM DAS DUAS ATIVIDADES. QUE DOIDO ESSE CÁLCULO!
26
Pau no Burro.
29+28 + 4 = 61
61 - 35 = 26
CERTO
Atividade 1 = A
Atividade 2 = B
Gostam da atividade 1 = n(A) = 29
Gostam da atividade 2 = n(B) = 28
Gostam das duas = n(A∩B)
Não gostam de nenhuma = n(Y)
35 = (29 - n(A∩B)) + n(A∩B) + (28- n(A∩B)) + n(Y)
35 = 29 + 28 - n(A∩B) + n(Y)
35 = 57 - n(A∩B) + n(Y)
n(A∩B) = 57- 35 + n(Y)
n(A∩B) = 22 + n(Y)
Se a questão diz que n(Y) é igual a 4, então 22 + 4 = 26
Questão correta
Gabarito: CERTO
Basta retirar dos 35 aqueles que não gostam das atividades: 35-4= 31, o que diz que o espaço Universo agora é de apenas 31 que ou gostam da atividade I; ou gostam da atividade II; ou gostam das duas atividades;
X : número daqueles que gostam das duas atividades.
Agora monta-se o conjunto da primeira atividade, que será: 29-x
Agora monta-se o conjunto da segunda atividade , que seria: 28-x
Agora somo o primeiro conjunto mais oo segundo conjunto mais o X
31= 29-x + 28-x + x=
31=57-x
X= 57-31
X= 26, logo o número daqueles que gostam das duas atividades será igual a 26
CERTO
35 TOTAL
35 - 4 = 31
29+28 = 57
57-31= 26
Gabarito:Certo
Principais Dicas:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!