-
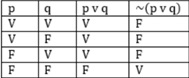
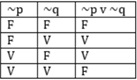
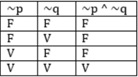
A proposição ~p --> q é equivalente a p V q ?
Não.
Na condicional temos apenas um caso em que a tabela fica falsa, V F, já na ou exclusivo temos dois V V e F F.
-
Eleizomar,
você fala em tabela, poderia explicar melhor isso.
Sou um zero à esquerda nessas questões.
Abraço.
-
A primeira proposição relata que a não eliminação é uma condição para a nomeação de Pedro Henrique, reescrevendo a proposição ficaria desta forma: Se Pedro Henrique não for eliminado na investigação social, então ele será nomeado para o cargo, isto é P1 = ~P->Q. A segunda se trata de uma disjunção exclusiva pela presença de dois conectivos ou(ou...ou), ficando da seguinte forma: P2 = P v Q.
A tabela verdade fica desta forma:
P ~ P Q ~P -> Q P v Q V F V V F V F F V V F V V V V F V F F F
Logo as proposições P1 e P2 não são equivalentes.
-
Consegui uma ótima explicação sobre tabela verdade na interntet
http:// http://www.youtube.com/watch?v=LwSZ0xIhtDo
-
Proposição Equivalência da negação
| (p e q) | ~p ou ~q |
| (p ou q) | ~p e ~q |
| (p-->q) | p e ~q |
| (p↔q) | Ou p Ou q |
Seja
P: Pedro Henrique é nomeado para o cargo
Q: Não eliminação na investigação social”
A proposições “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social” pode ser assim escrita: Se Q--->P. Logo é equivalente a (P e ~Q): Pedro Henrique não é eliminado na investigação social E é NÂO é nomeado para o cargo
-
Alguns professores e apostilas pregavam que para o Cespe "ou A ou B" seria equivalente a "A ou B", e não ao "Ou exclusivo", por isso respondi que esta questão estava certa no gabarito, e logicamente quebrei a cara.
Agora ficou claro, não existe tal entendimento por parte do Cespe. Eu espero...
-
Equivalência da condicional
P → Q
Se PH não foi eliminado na investigação social, então ele será nomeando para o cargo
P - PH não foi eliminado na investigação social
Q - Ele será nomeado para o cargo
Equivalência 1
¬P v Q
PH foi eliminado na investigação social OU ele será nomeado para o cargo
Equivalência 2
¬Q → ¬P
Se PH não for nomeado para o cargo, então ele foi eliminado na investigação social
-
Gente cuidado no comentário final da colega Patrícia Lira, pois ela equivocou-se colocando como a equivalência do p → q como p v ¬q e é o contrário (¬P v Q). Nega-se a 1 (no caso p), troca o sinal (→) por( v) e mantém a 2 (no caso q). O comentário do Alex está perfeito nas duas formas de equivalência da condicional.
-
Disjunção inclusiva e disjunção exclusiva não são a mesma coisa. Sejam A e B duas proposições. A: vou comprar um sapato, B: vou comprar um tênis.
Na disjunção inclusiva pode acontecer os seguintes cenários: Ou eu compro um sapato, ou eu compro um tênis ou eu compro ambos. Então em A V B, ou A é verdadeiro, ou B é verdadeiro ou A e B são verdadeiros que A V B será verdadeiro.
Na disjunção inclusiva, os dois cenários não podem acontecer simultaneamente, ou eu compro um sapato, ou eu compro um tênis. Mas nunca eu compro o sapato e o tenis juntos. Dai, A W B (disjunção exclusiva = W) é verdade somente se A = V e B = F ou A = F e B = V, nunca A = V e B = V ou A = F e B = F.
Para fixar: ou João é meu filho ou João não é (não tem como João ser e não ser meu filho). As 8h ou eu estou em casa ou estou no parque (não tem como eu estar em casa e no parque as 8h).
Então a questão é errada, pois Pedro Henrique é eliminado W Pedro Henrique é nomeado. No outro caso Pedro Henrique não é eliminado então é nomeado. Dai, temos Pedro Henrique é eliminado V Pedro Henrique é nomeado.
-
Pessoal, alguém pode me ajudar? Não entendi pq a questão está errada Segue meu raciocínio:
Questão: As proposições “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social” e “Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo” são logicamente equivalentes.
P = Pedro é nomeado para o cargo
Q = Pedro não é eliminado na investigação social
P <-> Q
P = Pedro é nomeado para o cargo
~Q = Pedro é eliminado na investigação social
~Q v P
A questão afirma que P <-> Q é equivalente a ~Q v P.
Para confirmar fiz a tabela lógica:
| P | Q | P <-> Q | | ~Q | P | ~Q v P |
| V | V | V | | F | V | V |
| V | F | F | | V | V | F |
| F | V | F | | F | F | F |
| F | F | V | | V | F | V |
O que eu fiz errado??
-
Respondendo ao colega acima.
O seu erro de raciocínio foi em construir a primeira proposição como a negação de uma bicondicional ~(P <-> Q) que realmente teria como equivalente
a disjunção exclusiva P v Q.
A primeira proposição quando diz FICA CONDICIONADA, quer dizer que uma proposição simples é condição para a outra. No caso ~P -> Q ( Se PH não for eliminado na investigação social, então ele será nomeado) A nomeação de PH para o cargo é CONDIÇÃO NECESSÁRIA à não eliminação na investigação social.
A equivalencia lógica de um condicional pode ser: ~Q -> ~P(contrapositiva) ....... ~P v Q (reescrita da condicional)
espero ter ajudado. abs
-
Um comentário extra:
Detestei essa nova ordenação e a renomeação dos assuntos de Raciocínio Lógico, aqui no site. O que era perfeitamente ordenado conforme os nomes dos assuntos cobrados nos editais de concurso, foi mudado pra um único tema: "p. Raciocínio Lógico-Psicotécnico". Os outros assuntos são referentes a matemática e nada se confunde com Raciocínio Lógico.
Já solicitei à equipe QC a revisão dessa "infeliz" mudança de assuntos e a reordenação de acordo como estava antes. Quem concordar, e quiser ajudar, fica o apelo a vcs para enviarem à equipe QC (Através do link "Atendimento") a sugestão de reordenação dos assuntos, conforme estava listada anteriormente aqui no site!
Grato!
-
“A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social”
P: Nomeação de Pedro Henrique para o cargo
~Q: Nao eliminação de Pedro Henrique na investigação social
P -> ~Q: Se Pedro Henrique foi nomeado para o cargo, entao não foi eliminado na investigação social
~ (P -> ~Q) = ~P V ~Q
(Equivalencia Correta) ~P V ~Q: Pedro Henrique não foi nomeado para o cargo OU não foi eliminado na investigação social
(Equivalencia apresentada na Questão) Q V P: "Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo”
Portanto, a questão é falsa.
-
P1: “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social".
P2: “Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo "Reescrevendo P1 teremos:
“Se Pedro Henrique é nomeado para o cargo, então ele não foi eliminado na investigação social "Lembrando que as equivalências da condicional são:
p→q = ~q→~p
e
p→q = ~p v q
Logo, uma proposição equivalente a P1 será:
“Se Pedro Henrique não foi nomeado para o cargo, então ele não foi eliminado na investigação social "Ou“ Pedro Henrique não foi nomeado para o cargo ou ele não foi eliminado na investigação social".
Resposta: Errado
-
Só pra todos não se confundirem, o prof. se equivocou ao colocar que p-->q é equivalente a ~p-->~q, pois o correto seria p-->q é equivalente a ~q-->~p.
Cuidado, pode ter sido erro de digitação.
-
''fica condicionada '' = Se, e Somente Se..., Logo a questão está errada, e o gabarito está correto.
-
As equivalências de P ->Q são essas:
1 - (¬Q -> ¬P) e
2 - (¬P v Q).
Lembrando que devemos inverter a ordem dos termos no primeiro caso.
-
Traduzi as frases em letras e como estão escritas e passei pra Tabela Verdade.
A <-> B
A v B
| A | B | A v B | A <-> B |
| V | V | F | V |
| V | F | V | F |
| F | V | V | F |
| F | F | F | V |
Gabarito ERRADO.
-
Como não existe equivalência entre condicional e a disjunção exclusiva fiz a questão passo a passo
| P | Q |~Q | P->~Q | Q V P |
| V | V | F | F
| V | P->~Q e Q V P
| V | F | V | V
| F
| não são equivalentes!!!!
| F | V | F | V
| F
|
| F | F | V | V
| V
|
-
Pessoal, cuidado com o comentário do professor, pois está errado. O mesmo afirma que P --> Q é equivalente a ~P --> ~Q, o que está completamente errado, a equivalência é entre P --> Q e ~Q --> ~P.
Cuidado com os comentários desses professores, já vi vários errados!
-
OBSERVAÇÃO: Muitos estão fazendo confusão em relação a condição suficiente e condição necessária.
Condição suficiente: Pedro Henrique é nomeado.
Condição necessária: Pedro Henrique não foi eliminado na investigação social.
Assim,
Se Pedro Henrique é nomeado, então ele não foi eliminado na investigação social. (Correta).
Se Pedro Henrique não foi eliminado na investigação social, então ele foi nomeado. (Errada).
A nomeação de Pedro fica condicionada a não eliminação na investigação social, e não o contrário.
-
Po, "fica condicionada" te induz a pensar que se trata de "se e somente se". Ao construir a tabela "N <-> ~E" e "E v N" (exclusivo) elas são equivalentes: FVVF. Ridículo essa falta de clareza por parte do CESPE. Erra-se a questão pelo enunciado mal feito, mesmo conhecendo a matéria. Alias, é gritante a quantidade de questões que ficam em aberto, dando chance pra escolha do gabarito mais conveniente...Se o gabarito fosse "certo", nenhum recurso derrubava a justificativa pífia: "Ele será nomeado somente se não for eliminado, portanto, o conectivo tratado é bicondicional".
-
Justificativa do Cespe
A afirmação “A nomeação de Pedro Henrique ao cargo fica condicionada à não eliminação na investigação social” tem o mesmo sentido de “Se Pedro Henrique não é eliminado na investigação social, então é nomeado ao cargo”, que por sua vez não é equivalente à afirmação do item. A existência do primeiro "ou" na afirmação do item caracteriza a disjunção exclusiva. Mantenha-se o gabarito do item.
Fonte: http://www.cespe.unb.br/concursos/DPF_12_ESCRIVAO/arquivos/DPF_ESCRIV__O_JUSTIFICATIVAS_DE_ALTERA____ES_DE_GABARITO.PDF
Dica: para quem ainda não sabe, nas provas da PF o Cespe divulga a justificativa de gabarito para todos os itens (100% da prova), de todas as disciplinas. É só abrir o PDF que eles colocam para "Justificativas de alteração de gabarito de itens".
-
Essa acertei com o conhecimento de saber que pode-se trocar "se,e somente se" por "ou..ou".
-
Erica, pensei quase da mesma forma que vc, inclusive tem outra questão semelhante derivada dessa mesma proposição que todos consideraram a proposição como condicional, mas eu a veja como uma proposição simples. O que fic condicionada à não eliminação na investigação social? A nomeação de Pedro.
-
Explicação do Professor está ERRAAADAAAAAAAA!!
Pede pra sair!!!
-
Corrijam-me se estiver errado, mas achei tantos comentário que só fizeram foi complicar ainda mais ...
Nao seria mais fácil dizer que a equivalência da disjunção exclusiva é NEGAR A 1a E USAR O CONECTIVO "SE E SOMENTE SE" e MANTER A 2a??
Ex.: A v B = ~B <-> B
A<-> ~B
-
Marquei como errada, pois entendi que a P1 é proposição simples, raciocínio correto?
-
A segunda proposição é uma disjunção exclusiva. Disjunção exclusiva não possui equivalência.
-
fica ligado no conectivo OU OU nao TEM sinonimo para ele
todas as vezes que vinher nas questoes marque sem medo ERRADO
-
CESPE é muito complicado. Nunca que “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social", é condicional. Se fosse, realmente estaria errada. Isso tá mais pra bicondicional.
Lamentável.
-
Putz acertei pq pensei que era uma prepos simples, nem conta.
-
As explicações dos professores na matéria de Lógica no PC, prefiro nem ler.
-
Comentário Eleizomar (primeiro comentário)
Simples e objetivo.
-
CUIDADO COM O COMENTÁRIO DO JOÃO SANTOS.
Disjunção exclusiva possui SIM equivalência, a mais comum é a bicondicional.
-
Eu fiz da seguinte forma:
Pedro ser nomeado = P
Pedro eliminado = Q
Então: “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social" = P ^ ~Q (Se levar em consideração que ambas as afirmações tem que acontecer para), ou P -> ~Q também se levarmos em consideração que desta forma ele pode não ser nomeado mesmo sem ser eliminado.
A negação do “E” é negar ambas e mudar o conectivo para “ou”. No caso de P ^ ~Q, a negação seria ~P v Q. E a negação do "Se... Então" é a do marido infiel (mantém a primeira esposa E nega a segunda). Assim o P -> ~Q fica P ^ Q.
Quando vamos ver “Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo" equivale à Q v P. Que é diferente das duas hipóteses (P ^ Q e ~P v Q).
Gabarito: ERRADO
-
Gabarito: errado
Fonte: minhas anotações de outras questões CESPE.
--
Cuidado! Existe sim uma equivalência da disjunção exclusiva: é a bicondicional. Destaco aqui as principais equivalências adotadas pelo CESPE:
Condicional:
p -> q = ~q -> ~p ( contrapositiva );
p -> q = ~p v q.
Disjunção:
p v q = ~p -> q.
Bicondicional:
p <-> q = ( p -> q ) /\ ( q -> p );
p <-> q = ( p /\ q ) v ( ~p /\ ~q ).
Disjunção exclusiva:
p v q = ~p <-> q. ( se não falha a memória, essa é a terceira vez que o cespe cobra hehe )
"É necessário sempre acreditar que um sonho é possível
Que o céu é o limite e você, truta, é imbatível
Que o tempo ruim vai passar, é só uma fase
Que o sofrimento alimenta mais a sua coragem" Viver é desafio - Racionais mc's.
-
A equivalência ocorreria se fosse: "Pedro Henrique é eliminado na investigação social OU é nomeado para o cargo."
-
A questão propõe que é equivalente P -> Q e P V Q
Se então não se nega com Ou Ou.
Gab.: Errado
-
Muitos, muitos, muitos comentários equivocados...
Moçada vamos ter mais ZELO, pesquisar ou estudar o assunto, antes de escrever qualquer coisa.
Essa questão é bem mais aprofundada do que parece.
Quando o examinador diz: “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social" , o examinador está trazendo uma CONDICIONAL INVERTIDA.
Explico:
"Se A está condicionado a B", isso equivale a: "Se B então A."
Na notação proposicional ficaria: B -> A
A proposição que A QUESTÃO TROUXE é: “A nomeação de Pedro Henrique para o cargo (A) / fica condicionada à não eliminação na investigação social (B)"
Esta mesma proposição na sua ordem NATURAL seria: "Se Pedro Henrique não é eliminado na investigação social (B) / então ele é nomeado para o cargo (A)"
Na notação proposicional ficaria: ( B -> A )
Para ela, existem DUAS EQUIVALÊNCIAS:
1) Pedro Henrique é eliminado na investigação social ou ele é nomeado para o cargo. ( ~B v A )
2) Se Pedro Henrique não é nomeado para o cargo então ele é eliminado na investigação social. ( ~A -> ~B )
Nenhuma dessas duas equivalências confere com a disjunção EXCLUSIVA que a questão trouxe como possível equivalência: Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo ( B v A )
Então, gabarito: ERRADA
Espero ter contribuído!
Abraço
-
Podemos reescrever a primeira proposição da seguinte forma: “Se Pedro Henrique não for eliminado na investigação social, então ele será nomeado para o cargo”. Seja:
p: Pedro Henrique não será eliminado na investigação social
q: ele será nomeado para o cargo
A proposição fica: p → q. Sabe-se que as duas hipóteses de equivalência para uma condicional são:
I) ~q → ~p
II) ~p v q
A alternativa apresenta como equivalente uma disjunção exclusiva e está ERRADA
-
Completando o que O Felipe Fernandes disse. Quando aparecer ou...ou se existe a possibilidade de ambas proposições serem verdadeiras, devem ser encaradas como disjunção inclusiva e se não existe como é o caso da questão, é uma disjunção exclusiva que não possui equivalência com a condicional.Têm muitos comentários que a galera faz no chutômetro e isso acaba atrapalhando quem ainda tá aprendendo.
-
Condicionada não é bicondicional. O próprio nome já fala, é uma condição, ou seja, se... , então.
Cuidado com os comentários errados.
-
FICA BI-CONDICIONADA
E NÃO CONDICIONADA
-
P1: “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social".
P2: “Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo "Reescrevendo P1 teremos:
“Se Pedro Henrique é nomeado para o cargo, então ele não foi eliminado na investigação social "Lembrando que as equivalências da condicional são:
p→q = ~q→~p
e
p→q = ~p v q
Logo, uma proposição equivalente a P1 será:
“Se Pedro Henrique não foi nomeado para o cargo, então ele não foi eliminado na investigação social "Ou“ Pedro Henrique não foi nomeado para o cargo ou ele não foi eliminado na investigação social".
Resposta: Errado
-
Engraçado muita gente ir na conversa dos professores de caca, confiando cegamente nos comentários que eles fazem sem sequer colocá-los em causa, fruto de má preparação em teoria. Pensam que fazer copy paste de comentários de professores de caca aprendem alguma coisa? Não! Leiam o que o Felipe Fernandes Bezerra escreveu e aprendam!
-
Galera uma dica simples
Não existe equivalência com ou ou, logo questão errada
-
So quer saber se a equivalência do SE ENTÃO pode ser feita com o (OU...OU).
Errado
-
Ou ...Ou não possui equivalência!
Fim!
-
Se alguém puder me ajudar, minha interpretação foi a seguinte:
n = Nomeação de Pedro
e = Eliminação na investigação social (logo, ~e = Não eliminação na investigação social)
A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social [~e -> p]
Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo [e v p]
Comparando-se:
[~e -> p] = [e v p]
I. v (V) v = f (V) v
II. v (F) f = f (F) f
III. f (V) v = v (F) v
IV. f (F) f = v (F) f4
Logo, gabarito errado.
-
Minha contribuição.
Equivalência da condicional:
1° Caso: A -> B (é equivalente a) ~B -> ~A
2° Caso: A -> B (é equivalente a) ~A v B
3° Caso: Passar a mesma ideia, utilizando palavras diferentes.
Abraço!!!
-
Pessoal, cuidado, vi muita resolução que acredito estar errada aqui, inclusive as mais votadas.
Eu discordo da resolução apresentada pela grande maioria das pessoas aqui. Para mim fez sentido resolver da maneira como vou apresentar abaixo. Se alguém puder comprovar me passando um material confiável que prove o contrário, agradeço.
-----------------------
-Proposição dada:
“A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social”
-Vamos escrever:
"A nomeação de Pedro Henrique para o cargo" = A
"fica condicionada à não eliminação na investigação social" = B
-Logo, temos:
A fica condicionado a B
-A meu ver, isso é equivalente a:
Se A então B
-Diferente do que a maioria falou, dizendo que é equivalente a "Se B então A"
Montando a tabela verdade de "Se A então B" percebe-se que é diferente de "Ou A ou ~B", logo, não são equivalentes.
-----------------------
Pessoal, para sustentar minha resolução, veja bem:
“A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social”
Isso significa, claramente (sem ficar tratando de proposições agora, só no bom senso) que Se Pedro foi nomeado no cargo, então ele obrigatoriamente não foi eliminado na investigação social. Ou seja, Se (foi nomeado) então (não foi eliminado). É obrigatório que, se ele vai ser nomeado, ele não tenha sido eliminado.
O inverso não é válido. NÃO poderíamos dizer obrigatoriamente que Se Pedro não foi eliminado na investigação social, ele será nomeado. Ora, ele pode muito bem ser aprovado na investigação social mas ser reprovado numa fase posterior: na avaliação psicológica, no curso de formação, na avaliação médica... Logo, está errado dizer que a proposição é equivalente a "Se Pedro não foi eliminado na investigação social, ele será nomeado". Por outro lado, seria correto dizer "Se Pedro foi nomeado no cargo, então ele não foi eliminado na investigação social". Questão de bom senso.
-----------------------
Observação: Fazendo do meu jeito (Se A então B) ou do jeito da maioria (Se B então A) o gabarito ficaria errado de qualquer forma.
-
De acordo com o Professor do Qconcursos:
P1: “A nomeação de Pedro Henrique para o cargo fica condicionada à não eliminação na investigação social".
P2: “Ou Pedro Henrique é eliminado na investigação social ou é nomeado para o cargo "
Reescrevendo P1 teremos:
“Se Pedro Henrique é nomeado para o cargo, então ele não foi eliminado na investigação social".
Lembrando que as equivalências da condicional são:
p→q = ~q→~p = ~p v q
Logo, uma proposição equivalente a P1 será:
“Se Pedro Henrique foi eliminado na investigação social, então ele não é nomeado'' ~q -> ~p
ou
''Pedro Henrique não foi nomeado para o cargo ou ele não foi eliminado'' ~p ou q
-
Equivalêncas: P -> Q
1º NEUMA (NE ou MA) - NEGA a primeira e MANTÉM a segunda - com o conectivo "ou" entre as proposições.
P -> Q
2º IVETE NEGA - INVERTE a ordem e NEGA elas (proposições)
P -> Q
Notem que na segunda opção o conectivo permanece o mesmo (Se -> então).
Gab. ERRADO
-
Podemos reescrever a primeira proposição da seguinte forma: “Se Pedro Henrique não for eliminado na investigação social, então ele será nomeado para o cargo”. Seja:
p: Pedro Henrique não será eliminado na investigação social
q: ele será nomeado para o cargo
A proposição fica: p → q. Sabe-se que as duas hipóteses de equivalência para uma condicional são:
I) ~q → ~p
II) ~p v q
A alternativa apresenta como equivalente uma disjunção exclusiva e está ERRADA
Arthur Lima | Direção Concursos
-
Gabarito:Errado
Principais Regras:
Se...Então
1) Mantém o conectivo + Inverte as Proposições + Nega
2) Regra do NOU: Retirar o conectivo + Nega a 1º frase + OU + Mantém a 2º frase
OU
1) Regra do NOU (trocado): Troca por Se...Então + Nega a 1º + Mantém a 2º frase
DICA: Lembre se de que quando for NEGAR, deve usar as regras da Lógica de Negação.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões de outras matérias. Vamos em busca da nossa aprovação juntos !!
-
p1 é proposição simples, nao tem equivalencia
-
Gab. E
Método Telles:
Equivalência:
Em uma frase condicional temos 3 casos:
1° Se ele colocar o Se nas 2 (pergunta e resposta) volto negando as duas.
Ex: Se não chove, pato late.
Equiv. : Se pato não late, chove
2° Se no lugar do então o examinador colocar o conectivo OU eu nego a primeira e mantenho a segunda.
Ex: Se não chove, pato late.
Equiv. : Chove ou pato late.
3° Falar a mesma coisa (mesma ideia)
Ex: Se não chove, pato late.
Equiv. Como não chove, pato late.
-
Só pelos conectivos já dá pra marcar como errada:
I) p → q
II) ~q → ~p
III) ~p v q
-
Alguém também tem dificuldade em identificar a proposição quando é condicional poderia me ajudar? Fico presa nas orações com o “se” e quando sai do padrão erro a questão!

 " - será verdadeira quando ambas forem verdadeiras ou ambas forem falsas.
" - será verdadeira quando ambas forem verdadeiras ou ambas forem falsas.