-
Para ser uma Tautologia independe dos valores lógicos de A e C, basta que B seja V. Pois, a única forma de não se ter uma tautologia será no caso de se ter os valores logicos V --> F (F) na tabela verdade. MACETE: "Vera Fischer é Foda".
-
Errei a questão, depois analisando meu erro percebi que o X da questão está aqui: no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu.
Fazendo a tabela-verdade, encontraríamos que a proposição (A ^ ~C) -> B possui uma possibilidade de ser falsa, que é quando A é verdadeiro, C é falso e B é falso. Porém, foi dito no enunciado que "Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu". Com essa informação, fica impossibilitada a opção de A ser verdadeiro, C falso e B falso.
Espero ter ajudado.
-
Oi!
Resposta: E. Abordagem nova (nunca tinha visto) em relação a estas questões de tabela verdade. Exige atenção, pois uma questão aparentemente "ganha" pode te dar uma rasteira!Explicitando a tabela verdade temos:
A B ~C (A^~C)=>B
V V F V
V V V V
V F F V
V F V F
F V F V
F V V V
F F F V
F F V V
À primeira vista, parece-nos contingência; mas a questão diz "Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu. "
As linhas de 3 a 6 da resposta da tabela (sublinhadas) não podem ser consideradas, já que com base nos dados do problema José e Luis tiram férias juntos; portanto, as linhas da tabela em que A e B (José e Luis) têm valores lógicos diferentes, não serão consideradas! *Ele negou o C, então Mário não tirou férias em janeiro de 2013.
Ufa!!!
Natália.
-
Pessoal, esta eu resolvi fazendo apenas a tabela verdade da proposição (A∧~C) →B e, conforme verificado, se trata de uma tautologia, pois todos os valores são verdadeiros.
-
(V∧F) →V
F→V
V
-
Olá,
Essa questão pelo conceito de tautologia você resolveria. Os dados escritos são só para lhe enganar e você perder tempo. A questão afirma que uma tautologia "depende" dos valores lógicos e também afirma que uma tautologia pode ser "verdadeira ou falsa". O que contradiz totalmente a regra. Por isso o gabarito é Errado.
Regra: "TAUTOLOGIA É QUANDO UMA PROPOSIÇÃO COMPOSTA É SEMPRE VERDADEIRA,
INDEPENDE DOS VALORES LÓGICOS DAS PROPOSIÇÕES SIMPLES QUE A COMPÕE"
De fato quando você desenha a tabela verdade da proposição (A^~C)→B, é verificado que esta proposição realmente não é uma tautologia pois apresenta uma condição de ser falso.
Mas ao conceituar o que é tautologia, essa afirmativa torna o gabarito Errado.
A ~C (A^~C) B (A^~C)→B
V F F V V
V V V V V
V F F F V
V V V F F
F F F V V
F V F V V
F F F F V
F V F V V
-
“A: José tirou férias em janeiro de 2013”; V
“B: Luís tirou férias em janeiro de 2013”; V
“C: Mário tirou férias em janeiro de 2013”, V
proposição (A∧~C) →B (A=VERDADE e NÃO C =FALSA) = FALSA ENTAO B= V
dica: primeiro resolve o que esta dentro dos parenteses.
TABELA VERDADE DO CONDICIONAL
F V = V
-
Tá, mas suponhamos que A=v e ~c=v e B=F, então seria F... Não seria então uma tautologia...Viajei ou não entendi o que a questão queria?
-
Questão ERRADA!
Não é umaTautologia, isto é fato. Daí, a banca continua a afirmação...isto é,dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa.
Na tabela-verdade dessa proposição determinamos porque a questão está incorreta:
| A | B | C | ~C | (A ^ ~C) | (A ^ ~C) → B |
| V | V | V | F | V | V |
| V | V | F | V | V | V |
| V | F | V | F | V | V |
| V | F | F | V | V | V |
| F | V | V | F | F | F |
| F | V | F | V | V | V |
| F | F | V | F | F | V |
| F | F | F | V | V | V |
Independe de A, B ou C serem verdadeiras ou falsas, a proposição será SEMPRE VERDADEIRA.
Espero ter contribuído.
Forte abraço e bons estudos.
-
Ai!!! Errei só o finalzinho da questão por não ter interpretado corretamente. Infelizmente acontece...
-
(A∧~C) →B
B → (A ^ ~C) = V, valor as proposições com V. B → A ^ B →~C = V ,como C é o único que nega, independente de seu valor, haverá tautologia. v → v ^ v → (v ou f) → v = tautologia.
-
Lembrando
que: “Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês
que José saiu de férias, ou Luís ou Mário também saiu”.
Assim,
teremos duas possibilidades, José saiu de férias no mesmo mês com Luís ou com Mário, logo:
1º) Opção.
A: José tirou
férias em janeiro de 2013; (V)
B: Luís tirou
férias em janeiro de 2013; (V)
C: Mário
tirou férias em janeiro de 2013; (F)
(A∧~C) →B – (V ^ ~F) →V = (V ^ V) →V = V→V= V
2ª) Opção.
A: José tirou
férias em janeiro de 2013; (V)
B: Luís tirou
férias em janeiro de 2013; (F)
C: Mário
tirou férias em janeiro de 2013; (V)
(A∧~C) →B – (V ^ ~V) →F = (V ^ F) →F = F→F = V
Assim, é
correto afirmar que a proposição (A∧~C)
→B é uma tautologia.
Logo a
resposta é: Errado.
-
Tautologia é uma proposição composta que será sempre verdadeira independente dos valores lógicos das proposições simples que a compõem, logo não é preciso fazer nenhuma tabela na questão pois o próprio conceito já está errado ao afirmar que depende dos valores da proposição para ser tautologia.
-
Não é uma tautologia. Essa parte está correta. O erro está nessa afirmação "dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa".
Quem fez a tabela-verdade, peço que olhem a primeira e a última linha da tabela-verdade. Na primeira linha, A, B e C são valorados como verdadeiras, notem que o resultado final também dá verdadeiro. Agora olhem na última linha da tabela. A, B e C estão todos valorados como falsos, mas o resultado final também dá verdadeiro.
Ou seja, independentemente de A, B ou C serem valorados como verdadeiros ou falsos, no preenchimento da tabela, o resultado será sempre verdadeiro. Aí está o erro. Quase que imperceptível.
GABARITO: ERRADO.
-
A questão está certa até "tautologia"; a partir daí eles dão o conceito de contingência...nem precisa de tabela-verdade.
Como os demais, errei por pura "afobação" e desatenção. :P
-
Nessa questão há uma casca de banana maldosa!
Mas lendo-a com atenção, dá para resolver tranquilamente.
O pulo do gato está justamente no enunciado. Vejam só:
"No mês que José saiu de férias, ou Luís ou Mário também saiu."
Simbolicamente: A -> B v C
Então teremos: V -> V/F v F/V
A disjunção exclusiva só será verdadeira quando houver uma sentença "V" e outra "F". Desse modo, concluímos que a disjunção exclusiva da questão será sempre "V".
V -> V v F = Verdadeira.
Agora vamos à tabela-verdade da proposição dada:
| A | B | C | ~C | (A ^ ~C) | (A ^ ~C) → B |
| V | V | V | F | V | V |
| V | V | F | V | V | V |
| V | F | V | F | V | V |
| V | F | F | V | V | V |
| F | V | V | F | F | F |
| F | V | F | V | V | V |
| F | F | V | F | F | V |
| F | F | F | V | V | V |
Note que, quando ocorreu:
A = V e B = V/F e C = V/F (condição dada pelo enunciado), a condicional foi sempre verdadeira.
Podemos concluir então, que se trata de uma tautologia.
-
Solução: ERRADO.
Levando em consideração o enunciado na questão , os únicos valores lógicos que A, B eC podem assumir são estes :
A: Só pode ser verdadeiro V. Porque está se considerando que José tirou férias.
B: V se C for F e F se C for V.
C: V se B for F e F se B for V.
Assim, colocando todos as situações possíveis em (A∧~C) →B
| A | B | C | (A∧~C) →B |
| V | V | F | V |
| V | F | V | V |
Logo, a fórmula dada será sempre uma tautologia.
-
Depois de ver todos os comentário e refletir e refletir e xingar o CESPE e tal, achei o erro: ( Eu acho rs).
Vamos analisar a questão. Há 2 pontos importantes e uma pitada de português.
[...] no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu.
Com base nessas informações, julgue os itens que se seguem.
Considerando-se as proposições “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”, é correto afirmar que a proposição (A∧~C) →B não é uma tautologia (Correto) , isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa (Errado).
1° A Proposição (A∧~C) →B de fato não é uma tautologia : Se fizer a tabela verdade encontrará os valores : VVVFVVVV
A pitada de português: Este "ela pode ser verdadeira ou falsa", o pronome ELA não se refere a palavra tautologia como muitos colocaram e sim se refere a palavra proposição.
2º Sendo assim, a preposição Não pode ser verdadeira ou falsa como afirma a questão. Veja A=V pois José saiu de férias, B e C podem ser V ou F, sempre opostos porque ou Luís ou Mário saíram de férias. Porém, na proposição o C está negado (~C), o que faz com q o B e (~C) tenham os mesmos valores e faça com que a proposição tenha valor verdadeiro.
Veja: A = V B=V/F C= V/F ~C = V/F
(A∧~C) →B
(V ^ V)→ V
(V)→V = V
ou(A∧~C) →B
(V^F) →F
(F)→ F = V
O Certo seria: Considerando-se as proposições “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”, é correto afirmar que a proposição (A∧~C) →B não é uma tautologia , isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela é verdadeira.
-
humm acho que uma forma mais simples é interpretar a tabela verdade que foi dada:
(A ^ ~C) -> B = assumindo que tudo seja verdade, fica:
(V ^ F) -> V = V
Assumindo que tudo seja falso, fica:
(F ^ V) -> F = V
Não tem como ficar falso, logo é um tautologia.
Força e Foco!
-
Galera, encontrei uma solução simples para resolver esta questão.
Perceba-se que, levando em conta a afirmativa "Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu", podemos admitir duas alternativas, quais sejam: "A" é equivalente a "B", ou a é equivalente "C".
Deste modo:
1.A=C
(A^~C)->B ==> (A^~A)->B
Como A^~A é uma contradição, será sempre falsa e, consequentemente a proposição composta será sempre verdadeira nesta hipótese, independentemente do valor de B.
2.A=B
(A^~C)->B ==> (A^~C)->A
Para a condicional ser taxada como falsa é preciso que o proposição antecedente (A^~C) seja verdadeira, e o precedente seja falso (A), entrementes, se admitirmos que "A" seja falso, o termo antecedente nunca poderá ser verdadeiro. Assim, neste caso a proposição sempre será verdadeira.
-
Questão muito maliciosa! Não precisava desenvolver nenhum raciocínio, exigindo apenas que o candidato soubesse o conceito de Tautologia. Quem leu rápido e partiu para resolução da tabela verdade, se complicou.
-
Errei a questão, pois parti para a tabela verdade. Dai, analisando melhor a questão, percebi que nesse caso não se deve fazer a tabela verdade porque no ENUNCIADO da questão já diz que no mês de janeiro jose tira férias, logo não existe a possibilidade dessa proposição ser falsa e na tabela verdade ela é testada como verdadeira e como falsa. Além do mais, na tabela verdade é testada a possibilidade em que tanto a proposição B como a C são verdadeiras ao mesmo tempo, o que também é excluído pela leitura do enunciado. Logo, dá até para fazer a tabela verdade, porém com o cuidado em levar todas essa observações em conta para considerar apenas as possibilidades que estão de acordo com o enunciado da questão.
Vejamos a tabela verdade a seguir, apenas com as possibilidades que se enquadram no enunciado:
A B C ~C (A ^ ~ C) (A ^ ~C) -> B
v v F V V V
v F V F F V
-
Eu apenas assumi o seguinte: "A", pode tirar férias no mesmo mês de "B" ou de "C" mas "B" e "C" não podem tirar férias no mesmo mês, então:
A: José tirou férias em janeiro de 2013 = V
B: Luís tirou férias em janeiro de 2013 = V
C: Mário tirou férias em janeiro de 2013 = F
(A∧~C) →B
V∧V→V
V→V
No Se...então a proposição só será falsa quando a primeira for verdadeira e a segunda for falsa. Como o resultado disse é verdadeiro e É TAUTOLOGIA e a questão afirma não ser tautologia então só por isso já posso afirmar que a questão está errada.
Vamos agora assumir diferente e conferir se daria o mesmo resultado
A: José tirou férias em janeiro de 2013 = V
B: Luís tirou férias em janeiro de 2013 = F
C: Mário tirou férias em janeiro de 2013 = V
(A∧~C) →B
V∧F→F
F→F
Mais uma vez confirmamos que é uma tautologia portanto a afirmação da questão está ERRADA
-
Muito comentário falando que a equação (A e ¬C) --> B é uma tautologia. Não é! Se você fizer a tabela-verdade com atenção, verá que há apenas uma forma em que dá falso: a famosa "Vera Fisher"! Logo, a questão está errada não por dizer que a questão não é uma tautologia, mas sim por dizer que será V ou F, a depender dos valores de A, B e C! Mentira! Se B for F, será F, seja lá o caso que apareça! Atenção!
-
GABARITO: ERRADO
Questão complexa e polêmica, muitos colegas aqui estão confundindo mais do que ajudando! mas com a ajuda de um e outro consegui chegar ao entendimento e vou compartilhá-lo, ok?
Na verdade devemos dividir a questão em 3:
1ª ETAPA: observar o enunciado: José tirou férias ou com Luís ou com o Mário e observar também que quando a questão diz que pode ser verdadeiro ou falso, na verdade ela se refere a PROPOSIÇÃO, e não a TAUTOLOGIA... essa é a chave da questão (por isso eu errei, ao menos).
2ª ETAPA: É realmente uma tautologia? devemos procurar uma resposta que negue essa possibilidade:
(A ^ ¬C) > B Aqui precisamos de um resultado FALSO pra provar que não é tautologia: V > F = F
(V ^ ¬F) > F
(V ^ V) > F
V > F
F Portanto ficou provado que existe uma po sibilidade ao menos de ser Falso, não é Tautologia
3ª ETAPA: Resolvendo a questão... ou seja, muita interpretação do problema. A questão disse que a depender dos valores de A, B ou C, o resultado pode ser V ou F, então mãos à obra:
OBS: lembremos que "A" tirou férias ou com "B" ou com "C", portanto, as proposições "B" e "C" obrigatoriamente não podem ser ambas verdadeiras, nos dando duas possibilidades:
(A ^ ¬C) > B Aqui eu atribui a C = V B = F
(V ^ ¬V) > F
(V ^ F) > F
F > F
V
(A ^ ¬C) > B Aqui eu atribui a C = F B = V
(V ^ ¬F) > V
(V ^ V) > V
V > V
V
Portanto, como vimos, ambas são necessariamente verdadeiras, contrariando o enunciado que diz poder ser V ou F, por isso a questão está errada!
Espero ter contribuído, levei muito tempo queimando os neurônios nessa questão!
A dificuldade é para todos, forte abraço!
-
Concordo com o amigo Raphael Martins que comentou em 14 de Julho de
2014, às 21h57... a questão se resolve apenas sabendo o conceito de
Tautologia, a saber:
SÃO AS PROPOSIÇÕES COMPOSTAS SEMPRE VERDADEIRAS, INDEPENDENTEMENTE DOS VALORES LÓGICOS DAS PROPOSIÇÕES SIMPLES QUE AS COMPÕEM.
Já a questão informa o seguinte:
"...é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto
é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser
verdadeira ou falsa."
ORA, TAUTOLOGIA SERÃO AQUELAS
QUE O RESULTADO DA TABELA VERDADE SEMPRE SERÁ VERDADEIRO, E NÃO
VERDADEIRO OU FALSO, AFINAL ASSIM TODAS AS PROPOSIÇÕES SERIAM
TAUTOLOGIA.
-
A resposta é simples: para que (A^~C)->B não seja uma tautologia, é necessária a seguinte condição: VAL(B)=F VAL(A)=V e VAL(C)=F ok!
porém ele diz no enunciado o seguinte: no mês que José saíu de férias ou Mário ou Luiz também saiu. Ele usa o "ou..ou" ou seja é uma alternativa mutuamente exclundente, por conseguinte como a proposição B pela condição acima é falsa, obrigatoriamente a proposição C deve ser verdadeira o que contraria a condição para não ser tautologia. Logo (A^~C)->B é uma tautologia.
-
Pela tabela completa não seria tautologia A
B
C
~C A ^ ~ C (A ^ ~ C) --> B
4
V
F
F V V F
...porém uma vez que no enunciado José sai de férias ou com Luís ou com Mário então temos sempre que se B = V então C = F e vice-versa.
Podemos eliminar da tabela verdade completa a linha 4, já que nesta linha B e C estão como F. O que nos dá, agora sim, uma tautologia.
-
É só fazer a tabela verdade para ver que não é tautologia, não entendi o comentário do professor ou eu não sei fazer a tabela verdade.
-
Caros colegas, sob o meu entendimento:
Essa questão deve ser analisado pelo seguinte ponto de vista:
A questão diz: Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu.
Ou seja: Quando José saiu de férias, mais alguém saiu de férias.
Depois informa:
Considerando-se as proposições “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”, é correto afirmar que a proposição (A∧~C) →B não é uma tautologia
Logo, de acordo com a questão, a proposição apresentada é: Se José tirou férias em Janeiro de 2013 E Mario NÃO tirou férias em Janeiro de 2013, então Luís tirou férias em Janeiro de 2013.
A única chance dessa afirmação ser falsa, seria:
1 - Fosse verdadeiro que José tirou férias em Janeiro de 2013;
2 - Fosse verdadeiro que Mário NÃO tirou férias em Janeiro de 2013;
3 - Fosse falso que Luís tirou férias em Janeiro de 2013.
Ou seja, (V ^ V) -> F
Dai se concluiria que José tirou férias em Janeiro de 2013, Mário NÃO tirou férias em Janeiro de 2013, Luís NÃO tirou férias em Janeiro de 2013. - ESSA SERIA A ÚNICA POSSIBILIDADE DE SER FALSA A PROPOSIÇÃO.
ORA, Mas isso é impossível segundo o texto associado à questão, que afirma: "... no mesmo mês que José saiu de férias, OU Luís OU Mário também saiu."
Portanto, pelo texto associado, obtém-se que ela não pode ser falsa.
Portanto ERRADA
-
Errado.
Questão simples, as proposições A, B e C são verdadeira pois o autor NÃO disse nada a respeito (essa é a regra). Se B é verdade é condição para a proposição ser verdadeira.
( ? ^ ?) --> V = V
Pra não ser tautologia ai sim ia depender da 1ª proposição ser VERDADEIRA do B ser FALSO. Ex.: (v ^ v ) --> F = F
Bons estudos!!!
-
GABARITO: ERRADO
Segui o mesmo raciocínio da nossa colega Rosane Aguiar descrito em outra questão.
TAUTOLOGIA: Para saber se é tautologia é só substituir os elementos por F e se no final dar verdadeiro considera-se tautologia.
Vejam:
F ^ ~ F -> F
F ^ v -> F
F -> F
V
Prático e rápido!
Bons estudos!
-
Quem fez a tabela dá um HOPE!
Gabarito : errado
-
Assertiva ERRADA.
Acho que o pessoal está pensando demaaaaaais antes de partir pro que a questão realmente quer saber. A questão diz "[...] é correto afirmar que a proposição (A∧~C)→B não é uma tautologia [...]". No meu ver, é só resolver este trecho para matar a questão.
Para descobrir se uma proposição composta é tautologia é só substituir as letras por F (falso) e resolver a proposição. Se der V (verdadeiro) no final é porque ela é uma tautologia:
(A ^ ~C) → B (muda as letras para F)
(F ^ ~F) → F (agora resolve)
(F ^ V) → F
F → F
V (como deu V no final é porque a proposição é uma tautologia)
-
galera o erro da questão estar em afirmar que a proposição (A∧~C) →B depende de A,B e C para ser uma Tautologia, o que não é verdade, afinal em uma proposição composta condicional só será falsa quando o consequente for F (v →F ) ou seja tanto faz o valor de A e C, o unico valor que pode influenciar no resultado é o de B !
TABELA DO VALOR DA CONDICIONAL
P Q P →Q
V V VV F F F F VF V V
-
Para quem quiser jogar na tabela, vale observar que a premissa só será falsa quando a B for falsa, já que a condicional não aceita VF. Por isso, tanto faz alterar A e C para V/F; F/V; V/V; F/F, porque o resultado sempre será V; a não ser que B seja Falso em alguma ocasião.
-
Não sei exatamente se é através desse esquema, mas o meu deu gaba errado também, visto que:
(A ^ ~C) =>B
V ^ F = F => V/F = Verdadeiro..
Reparem que na regra do condicional, sendo v ou f na segunda parte, sempre, será verdadeiro.
-
A B C ~C A^~C A^~C -> B
V V V F F V
V F V F F V Todos resultados verdadeiros é uma tautologia.
F V F V F V Gabarito da questão: Errado, pois afirma que NÃO é uma tautologia.
F F F V F V
-
Comentários:
Nossa
pessoal essa questão é do tipo “enche linguiça”!!!
**Quando o
cara dá uma proposição e afirma que ela não é uma tautologia é preciso apenas
confirmar isso. Nem leio o restante do enunciado.
Resolução pelo método (F) fode a
tautologia.
Vejamos:
(A^~C) -> B (atribui “F” pra geral)
Fica assim: (F^ (~F) ) -> F >>> (F^V) -> F >>> F -> F = V
Se após tudo
isso ela continua VERDADEIRA será uma tautologia.
Gabarito:
ERRADO
Bons
estudos.
-
Galera tem comentário errado aqui, sendo assim olhem o comentário da Núbia Silva é o melhor. Agora sim achei onde está o erro. Pois quem fizer através do método de atribuir "F" a todos os valores pode ter uma errada noção a respeito da questão. Ah e lembrando... a questão NÃO é uma TAUTOLOGIA!!!
-
Obrigada Roberto Faustino, realmente o comentário da colega Núbia Silva está melhor...
Foco, força e FÉ...
Bons estudos galera!!!!
-
Para saber se a proposição não é uma tautologia, basta forçar um
resultado falso. Nesse caso, (A ^ ~C) seria Verdade e B seria Falso. Para (A ^ ~C) ser verdade, A seria verdade e ~C seria verdade,
ou seja C seria falso.
Essa situação não existe: A verdade, C falso, B falso. Ou C,
ou B teria que ser igual a A.
Daí, conclui-se que, nas
demais situações que são possíveis, o resultado
é verdadeiro, ou seja, trata-se de uma tautologia.
-
Essa tabela da Graziela está ótima! Principalmente para errar tudo!
-
Primeiramente, sem utilizar os dados sobre José, Luís e Mario:
Fiz a Tabela Verdade da proposição (A∧~C) →B e só encontrei uma ÚNICA possível situação falsa, quando A^~C = VERDADEIRO e B = FALSO. (como quase todo mundo também concluiu).
Basicamente, a possibilidade de FALSO só ocorre quando A^~C = VERDADEIRO, ou seja, quando A = V e C = F.
Daí, eu voltei para os dados da questão:"No mesmo mês que José saiu de férias, ou Luís ou Mário também saiu".
Na única possibilidade da proposição ser falsa, a premissa de que Luís ou Mário viagem com José não é atendida, já que C e B são falsas.
Logo, essa possibilidade não existe. É impossível a proposição (A∧~C) →B ser falsa, considerando a premissa dada.
Considerei que a proposição é uma tautologia não pela Tabela Verdade unicamente, mas considerando a premissa dada também.
GABARITO = ERRADO
-
Caí na pegadinha do Cespe. Essa banca tem que ler com bastante atenção, os caras adoram colocaras casca de banana. Até "é correto afirmar que a proposição (A∧~C) →B não é uma tautologia" estava certo. Mas quando a banca coloca "isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa." então o item fica errado, porque numa condicional, para ser verdadeiro só depende da 2° proposição, no caso B.
. A melhor resposta é a do Gabriel Costa. Obrigado Gabriel.
-
Essa questão foi bem pagadinha mesmo, não basta saber fazer a tabela, tem que interpretar a frase seguinte.
-
o quadrado simboliza uma condicional?e como fica a bicondicional no caso?
-
Gab Errado!
Também errei.
Se você fez a tabela corretamente encontrou 1 valor F o que mostra que não é uma tautologia. OK marcou Certo e ERROU!
Mas continuando a questão o examinador disse:
''dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa.''
e aqui ↑ está o erro, o valor de B é que o único que poderia influenciar no resultado.
Muito obrigado Gabriel.
-
Acredito que a resposta não está na parte "dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa" e sim no enunciado da questão quando ele diz "no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu". Se considerar a proposição (A∧~C) →B falsa, ou seja, ela não é uma tautologia, o B necessariamente deve ser falso, logo, não foi o Luís que tirou férias no mesmo mês que José, só pode ser o Mario (C). Só que se a conjunção (A∧~C) for verdadeira (o que é necessário para tornar falsa a condicional), ~C será verdadeiro, contrariando o enunciado. Logo, não existe possibilidade da proposição ser falsa, pois contraria o enunciado da questão. É sim uma tautologia. É complicado explicar essas coisas então me desculpe se ficou confuso! :) Bons estudos!
-
Também vou contribuir:
Quem fez a tabela verdade encontrou os valores seguintes:
A. B. C. ~C. (A^~C) [(A^~C)->B]
V. V. V. F. F. V
V. V. F. V. V. V
V. F. V. F. F. V
V. F. F. V. V. F
F. V. V. F. F. V
F. V. F. V. F. V
F. F. V. F. F. V
F. F. F. V. F. V
Percebam que no enunciado da questão, José (A) tira férias ou com Luís(B) ou com Mario(C). A partir disso eu sei que eu não posso ter ao mesmo tempo os valores de A,B e C como verdadeiros, visto que se A e B for verdadeiro, ou seja José e Luís tiram férias em janeiro, logo C terá que ser falso, pois os três não tiram férias ao mesmo tempo.
Ao mesmo passo que eu não posso ter A como verdadeiro e B e C como falsos, pois José(A) não tira férias sozinho. Agora se vc voltar na tabela verdade, terá que eliminar as linhas que dão ao mesmo tempo os valores de A,B e C como verdadeiros e as linhas que têm apenas o valor de A como verdadeiro e BeC como falsos.
As linhas que tem como BeC verdadeiros ao mesmo tempo,também terão que ser eliminada, pois BeC não tiraram férias juntos no ano de 2013.
Ao eliminar essas linhas, teremos somente valores verdadeiros na tabela verdade, tratando-se portanto de uma tautologia. O que não condiz com a afirmação da questão.
Logo, gabarito Errado.
Gente, foi assim que cheguei ao resultado. Se por ventura eu estiver equivocado, alguém me corrija.
Bons estudos!
-
É um tipo de questão nova de tabela verdade, mas acredito que consegui entender. De fato, ao fazer a tabela verdade completa, não encontramos uma tautologia. Entretanto, a questão colocou uma condição.
Se analisarmos na tabela (que não vou colocar aqui pois já foi mostrada por outros), veremos que ao selecionar estritamente as linhas da condição (A sendo V, B e C sendo V ou F), teremos uma tautologia. Logo, só por isso, já dá pra matar que a questão está errada.
-
Será sempre tautologia!
GABARITO ERRADO
Se você considerar que José tirou férias em janeiro, logo a proposição "A" será verdadeira, e com isso ou Mário ou Luiz terá tirado férias com José mas não os dois, pois a questão afirma isso: Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu.
A = José tirou férias em janeiro (V)
B = Luiz tirou férias em janeiro (V)
C = Mário tirou férias em janeiro (F)
~C = Mário NÃO tirou férias em janeiro (V)
(A ^ ~C) --> B (V ^ F) --> V
V --> V
Agora se você considerar que "Luiz tirou férias em janeiro" como FALSO obrigatoriamente a proposição ~C será falsa:
(A ^ ~C) --> B
(V ^ F) --> F
F --> F
-
Muito bom o comentário de Rephael Martins!
Precisamos estar mais atentos...as vezes a resposta está no enunciado! precisamos prestar mais atenção...
Avante!
Bons estudos!
-
Pessoal, pra quem achou que o item está errado na explicação dada pra não ser tautologia, porque numa condicional só o consequente (no caso em questão, a proposição B) influenciaria o resultado, creio, pelo que estudei, que esta justificativa está errada. Realmente, numa condicional, só quando dá V > F (o famoso "Vera Fischer") é que é F, mas pra isso acontecer, como se pode ver, o ANTECEDENTE TEM QUE SER VERDADEIRO, porque se for F > F, tal proposição composta será V, logo não depende só do consequente, depende também do antecedente. E independente de qual tipo seja a proposição composta (condicional, conjunção, disjunção, bi-condicional, etc), a definição de tautologia é a mesma: a de que a proposição composta tem sempre o valor V independentemente do valor lógico das proposições parciais/simples que a compõem (de todas elas, e não de somente uma).
Acho que o enunciado dessa questão não é só pra encher linguiça não, influencia mesmo na resolução da questão. Errei porque só resolvi a tabela-verdade (que como vimos aparece um F), e não me atentei para os comandos da questão. Pelo que entendi, é tautologia sim, por isso o gabarito é Errado. Vejam o comentário do Wellington Bretas (lá em baixo, no começo dos comentários); achei bem coerente.
Espero ter contribuído.
-
Realmente, pelos comentários sobre o erro da questão estar no trecho "...dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa.", trata-se de uma conceituação divergente do conceito de tautologia.
Mas o erro não está apenas neste ponto, eu resolvi a questão de uma outra forma, pois percebi que o examinador tratou, em uma mesma questão, de duas matérias. Quais sejam: tautologia e associações lógicas.
Analisem e tentem responder usando tautologia e associações. E concreto, pois quando você acha quem é quem e quem tirou férias junto com José , nesta questão você vê que é um tautologia sim, e por isso a questão está errada, pois afirma que não é.
Não coloquei aqui a resolução pois para explicar ponto a ponto seria um mundo de informações.
-
Galera, esse tipo de questão (Trabalhando com condicionais e tautologias ao mesmo tempo) é recorrente no CESPE, derruba muito candidato bom e pode ser resolvido sem riscar o seu caderno...
Duvida?
Assista essa vídeo aula do saudoso professor Arthur Lima: https://www.youtube.com/watch?v=KzxKPanH0pE&index=25&list=PL70rxKg7qWNUxCli2Pj1Y1Yurv2Xk4r0k
-
O comentário do Raphael Martins está equivocado, não sei por que recebeu tanta curtida.
-
Substituindo por F de fato o resultado será uma tautologia. Alguém já tentou esse método em outras questoes e deu errado?
-
A palavra (falsa) no final deixou a assertiva errada.Conceito de tauto errado.
-
Comentário do professor do QC:
Lembrando que: “Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu”.
Assim, teremos duas possibilidades, José saiu de férias no mesmo mês com Luís ou com Mário, logo:
1º) Opção.
A: José tirou férias em janeiro de 2013; (V)
B: Luís tirou férias em janeiro de 2013; (V)
C: Mário tirou férias em janeiro de 2013; (F)
(A∧~C) →B – (V ^ ~F) →V = (V ^ V) →V = V→V= V
2ª) Opção.
A: José tirou férias em janeiro de 2013; (V)
B: Luís tirou férias em janeiro de 2013; (F)
C: Mário tirou férias em janeiro de 2013; (V)
(A∧~C) →B – (V ^ ~V) →F = (V ^ F) →F = F→F = V
Assim, é correto afirmar que a proposição (A∧~C) →B é uma tautologia.
Logo a resposta é: Errado.
-
Em relação ao comentário do professor, faltou uma terceira opção. Luís e Mário tiraram férias em janeiro, e José tirou férias em outro mês. .
(F e (~V) então V (F e F) então V resultando em uma sentença V. Assim, todas as sentenças são verdadeiras, o que é uma tautologia.
-
Comentários de david perin e Theo Xavier corretos, pois:
é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, (CORRETO), isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa (ERRADO, de maneira alguma uma tautologia pode ser falsa).
O Resultado da tabela da verdade chega numa linha Falsa, logo, impossível ser tautologia!
-
Há 3 situações possíveis para A, B e C e faremos os testes abaixo.
Situação 1:
(A∧~C) →B => V ^ V -> V => V ->
V = V
A: José tirou férias em janeiro de 2013 (V)
B: Luís tirou férias em janeiro de 2013 (V)
C: Mário tirou férias em janeiro de 2013 (F)
Situação 2:
(A∧~C) →B => V ^ F -> F => F ->
F = V
A: José tirou férias em janeiro de 2013
(V)
B: Luís tirou férias em janeiro de 2013 (F)
C: Mário tirou férias em janeiro de 2013 (V)
Situação 3:
(A∧~C) →B => F ^ F -> V => F ->
V = V
A: José tirou férias em janeiro de 2013 (F)
B: Luís tirou férias em janeiro de 2013 (V)
C: Mário tirou férias em janeiro de 2013 (V)
Resposta: Como todos os resultados são verdadeiros trata-se de uma TAUTOLOGIA (ERRADO)
-
G: ERRADO! Que Deus ilumine todos os estudantes.... MAS TENHAM CUIDADO!!! A questão mais curtida (Rhafael Martins) está errada!
1ª etapa: Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu. ( ele está dizendo que: para que uma linha da tabela verdade possa ser considerada pelo menos 2 deles precisam ser V) pq junto com José saiu pelo menos mais alguém....
2ª etapa: Interpretação da pergunta: Considerando-se as proposições “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”, é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ELA pode ser verdadeira ou falsa.
ELAAAAAAAAAAA QUEM???? CADÊ O SUJEITO DA ORAÇÃO??... O SUJEITO NÃO É A TAUTOLOGIA!!! O SUJEITO É A PROPOSIÇÃO! É A PROPOSIÇÃO QUE PODE SER V OU F dependendo dos valores de A, B e C.
Agora lembrem-se: na construção da Tabela Verdade vc deve eliminar as linhas em que aparecem 2 F - PQ A QUESTÃO DIZ QUE PELO MENOS 2 PEGARAM FÉRIAS AS MESMO TEMPO - entenda isso como 2V. São 8 linhas na tabela verdade mas só vou fazer 4 pq vcs já irão entender:
A B C ~C A^~C A^~C -> B
V V V F F V
V V F V V V
V F V F F V
V F F V V F (AHÃMMM!! "não é tautologia!" ERRADO! É SIM UMA TAUTOLOGIA pq de acordo com o enunciado não existe a possibilidade de José( = A) ter pegado férias sozinho; ou Luís (= B) ou Mário (= C) foi com ele.
-
Leiam o comentário da Patrícia Agostinho!
O do Raphael Martins tá errado! Faltou interpretação de texto..
-
Questão simples. Primeiro atribua valor verdadeiro (V) a todas: (A ^ ~C) ---> B = (V^F) ---> V. Isso dá VERDADEIRO.
Depois atribua falso (F) a todas: (A^~C) ---> B = (F^V) ---> F. Isso dá VERDADEIRO.
Portanto, em ambos os casos ocorreu tautologia, independente dos valores de a, b e c.
-
Verdade, Raimundo. Nesse caso deu certo, mas em outras não dá. Já errei questões aplicando essa regra, temos que tomar cuidado.
-
Só depende de 'B" se ele for for falso tem como ser tautologia ou contradição, se for verdadeiro vai ser tautologia.
O LANCHE DA QUESTÃO É O ENTENDIMENTO DO FINAL DA QUESTÃO, VISTO QUE FALA QUE NECESSITA DE A, B E C. MAS COMO DEMOSTRAMOS AQUI, BASTA VER O VALOR DO 'B".
-
De início a questão já se torna errada porque o examinador dispôs que um tautologia poderia ser verdadeira ou falsa, o que é incorreto, tendo em vista, que a tautologia só ocorrerá quando o valor lógico final for verdadeiro. Inobstante a isso passemos a resolução da questão.
Galera vamos analisar do ponto de vista da tabela verdade, caso ela fosse desenvolvida, ela completa seria da forma como ilustrada abaixo, ocorre que devemos nos atentar para o que dispõe a questão, ou seja: "Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu".
EM OUTRAS PALAVRAS O EXAMINADOR AFIRMOU QUE A PROPOSIÇÃO ´"A" É VERDADEIRA, VEZ QUE JOSÉ TIROU FÉRIAS.
DESTA FORMA O PRIMEIRO PASSO É EXCLUIR TODAS AS PROPOSIÇÕES DA TABELA VERDADE QUE LEVAM EM CONSIDERAÇÃO O "A" COMO FALSO.
O SEGUNDO PASSO É SE ATENTAR QUE O EXAMINADOR UTILIZOU O CONECTIVO "OU...OU"... DESTA FORMA, NECESSARIAMENTE LUIZ OU MÁRIO TIROU TIROU FÉRIAS, NÃO ACEITANDO A POSSIBILIDADE DE NENHUM DOS DOIS TIRAREM JUNTOS, OU AINDA DE NENHUM DELES TIRAR. DESTARTE TAMBÉM TEMOS QUE EXCLUIR DA TABELA VERDADE AS PROPOSIÇÕES QUE TEM COMO "B" e "C" COMO VERDADEIRAS OU FALSA SIMULTANEAMENTE.
A. B. C. ~C. (A^~C) [(A^~C)->B]
V. V. V. F. F. V = EXCLUÍDA PORQUE NÃO HÁ POSSIBILIDADE DE TODOS TIRAREM AS FÉRIAS JUNTOS
V. V. F. V. V. V
V. F. V. F. F. V
V. F. F. V. V. F = EXCLUÍDA PORQUE NECESSARIAMENTE LUÍS OU MÁRIO TEM QUE TIRAR FÉRIAS
F. V. V. F. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
F. V. F. V. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
F. F. V. F. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
F. F. F. V. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
Resumindo ficaria apenas duas possibilidades da tabela verdade a serem analisadas:
A. B. C. ~C. (A^~C) [(A^~C)->B]
V. V. F. V. V. V
V. F. V. F. F. V
Resultando assim, em uma tautologia, ou seja, quando o valor lógico final de uma proposição composta, é verdadeira. Contrariando o que dispõe a questão.
-
Interpretei a questão e entendi que José e mais um tiraram ferias no mesmo mês, logo, entre A, B e C, duas são V e uma é F. O A nós sabemos que já é V, então, fiz duas tentativas, coloquei o B como falso e a proposição deu V. Coloquei o C como F e a proposição deu V de novo. Logo, só pode ser tautologia. Da V de todo jeito. Simples assim. Bons estudos pessoal!
-
Peguei esta dica de uma outra pessoa em outra questão.
É só substituir tudo por F, se no final der V é uma tautologia.
(A^~c)-->B
(F^~F)-->F
(F^V)-->F
F-->F= V
-
Excelente questão.... tem que prestar atenção no enunciado ...
-
Lilian Camargos, mas a proposição (A^~C)->B em si não é uma tautologia, somente se nos restringirmos ao contexto da questão em análise.
-
Jonas Silva, ao contrário do que mencionaste no início do seu comentário, a questão não explica o que é tautologia erroneamente em momento algum.
Se vc se atentar, irá perceber que a explicação do item está corretíssima, uma vez que a questão diz que "NÃÃÃOO é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa".
Vc comentou como se estivesse escrito "é uma tautologia...", esquecendo do "não".
-
Jonas Silva , sua explicação resolveria o erra da CESPE se o enunciado ao invés de ter "...dependendo de A, B ou C serem verdadeiras ou falsas..." não mencionasse "A". Como você disse, o enunciado já informou que "A" é verdadeiro, mas como depois a pergunta vai no sentido de aferir possibilidade em que "A" também possa ser falsa, a tautologia não ocorre.
-
Jonas Silva, muito obrigada pela explicação.
Amei! E entendi.
-
Tive que observar muitos comentários dos colegas para entender "melhor" e o comentário de Núbia Silva é muito bom para essa questão. De toda forma, precisamos estar muito atento ao enunciado sempre!!!
-
Eita Jonas Silva, não sabia. Obrigado brother!
-
A = José tira férias em jan/13 / B = Luís tira férias em jan/13 / C = Mário tira férias em jan/13
Existem 2 opções: (No mesmo mês que José saiu de férias, ou Luís ou Mário também saiu !)
1) A = V; B = V e C = F.
(V e V) -> V = V -> V = V
2) A = V; B = F e C = V.
(V e F) -> F = F -> F = V
É uma tautologia !
Gabarito: ERRADO
-
O melhor comentário é o da Nubia
-
Sem muita lenga lenga.
Em sintese a questão pede o seguinte : dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa.
Ela realmente não é uma tautologia mas o que motiva isso é a alteração v ou f(vera fischer/vai fugir) de B nao de A e C.
-
Caí bonito nessa. kkkkk Ainda perdi tempo fazendo a tabela. Mesma coisa de nadar nadar e morrer na praia. kk
-
Fiz a tabela verdade, bem mais simples para saber a resposta!
-
Pessoal a questão diz: é correto afirmar que a proposição (A∧~C) →B não é uma tautologia
Resolvendo: F ^ ~F --> F
F ^ V --> F
F --> F
V
Afirmartiva: ERRADA, a prepoição é uma tautologia
-
O problema não é montar a tabela e sim prestar atenção no que a questão está pedindo --'
"é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa."
A B C (A^~C) -> B
V V V V
F F F V
Ou seja, se A B e C forem verdadeiras, o resultado final é Verdadeiro, se A B e C forem falsas, então o resultado final é Verdadeiro.
Errei por não prestar atenção no enunciado, simplesmente vi que não era uma tautologia e marquei Certa.
-
Essa questão é difícil, Lustosa do Alfa deu um show explicando como fazer e o por que de ser uma tautologia, se for fazer a tabela vai ter apenas uma linha da tabela que será FALSA, so que lendo o enunciado esse mesma linha MAIS outra duas da TABELA tb serão descartadas devido o enunciado da questão levando em conta o que o ENUNCIADO ASSIM DIZ.. top, mais é muito difícil... NÃO ESTOU SENDO PAGO PARA ISSO NEM AO MENOS TENHO INTERESSE ALGUM, mas para quem tem uns trocadimmm.. vale a pena comprar o 72H INSS, olha dicas topss.....
VALEU DEUS OS ABENÇOE!!!
-
É UMA TAUTOLOGIA INDEPENDENTE DAS VALORAÇÕES,EM CASO DE DÚVIDA,FAÇA A T.V
-
Errada, é uma tautologia.
Resolvi exatamente como o professor do QC.
-
PESSOAL FAÇAM A TV, E VERIFIQUEM POR SI MESMOS, ISSO NÃO É UMA TAUTOLOGIA!!!
CLIQUEM COMENTARIOS MAIS ÚTEIS E VERIFIQUEM O COMENTARIO DO COLEGA!
O QUE ESTÁ ERRADO NA QUESTÃO É O CONCEITO DE TAUTOLOGIA!!!
-
TAUTOLOGIA: Para saber se é tautologia é só substituir os elementos por F e se no final dar verdadeiro considera-se tautologia.
Vejam: ( NESTE CASO) diz sendo verdadeira ou falsa,não é tautologia vamos verificar :
F ^ ~ F -> F V ^ ~ V -> V
F ^ v -> F V ^ V -> V
F -> F = V V -> V = V logo está ERRADO pois f ou v da uma tautologia
Prático e rápido!
Bons estudos!
-
Pelo que entendi: enunciado "...José saiu de férias com Luís ou com Mário." Os três não juntos !!
Quando ele afirma “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”,B ou C são falsas. A com certeza é VERDADEIRA.
Podemos ter:[ A (V), B(V) e C(F)] OU [ A (V), B(F) e C(V)] . B e C nunca poderam ser VERDADEIRAS juntas. "...José saiu de férias com Luís OU com Mário."
Substituindo:
(A∧~C) →B
(V ∧ V) → V = VERDADEIRA
(V ∧ F) → F = VERDADEIRA
O enunciado que mata a questão"...José saiu de férias com Luís ou com Mário."
TAUTOLOGIA.
-
a proposição A^~C->B não é tautologia não. se fizer a tabela, quando o A for V, B for F e C for F, temos que V^V->F, ou seja, valor falso. Porém, no enunciado ele diz que "no mesmo mês que José saiu de férias, OU Luís OU Mário também saiu". OU...OU é disjunção excludente, ou seja, só pode ser um ou outro, mas não ambos, nem nenhum dos dois. então temos que a única possibilidade da proposição ser falsa (ABC-VFF) está excluída, já que José DEVE sair de férias com um dos dois, então B e C não podem ser falsos ao mesmo tempo.
-
MOLE, MOLE, GALERA!!!
O "X" da questão está no final da questão, onde é afirmado que:
"[...] é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa."
Esse "ela" refere-se, logicamente, à proposição (A∧~C) → B. Então, vamos lá.
[A ^ (~C)] → B
V ^ F = F → V = V
V ^ V = V → V = V
V ^ F = F → F = V
V ^ V = V → F = F
F ^ F = F → V = V
F ^ V = F → V = V
F ^ F = F → F = V
F ^ V = F → F = V
Note que a 2ª e a penúltima linha contraria a parte final do que foi afirmado, pois A, B ou C, independente de serem verdadeiras ou falsas,
(A ^ ~C) → B será sempre VERDADEIRA.
* GABARITO: ERRADO.
Abçs.
-
Questão sinistra!
-
"dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa." Essa definição de tautologia já torna a questão errada, não precisava fazer tabela nenhuma.
-
OTIMA OBSERVAÇÃO Nayara Lima, É UMA TAUTOLOGIA --->>> SEMPRE VERDADEIRA, E NAO FALSO E VERDADE!
QUEM SEMPRE É FALSO --->>> CONTRADIÇÃO
-
é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa. Errado!!!
[A ^ (~C)] → B
V ^ F = F → V = V
V ^ V = V → V = V
V ^ F = F → F = V
V ^ V = V → F = F
F ^ F = F → V = V
F ^ V = F → V = V
F ^ F = F → F = V
F ^ V = F → F = V
-
Galera, a questao diz que "ou luiz ou Mario tbm saiu de férias" disjunção exclusiva . Portanto, somente um poderia sair de férias com José! Bastava vc ficar atento ao texto que antecede a questão.
A. B. C. ~C. (A^~C) [(A^~C)->B]
V. V. V. F. F. V = EXCLUÍDA PORQUE NÃO HÁ POSSIBILIDADE DE TODOS TIRAREM AS FÉRIAS JUNTOS
V. V. F. V. V. V
V. F. V. F. F. V
V. F. F. V. V. F = EXCLUÍDA PORQUE NECESSARIAMENTE LUÍS OU MÁRIO TEM QUE TIRAR FÉRIAS
F. V. V. F. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
F. V. F. V. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
F. F. V. F. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIAS
F. F. F. V. F. V = EXCLUÍDA PORQUE NECESSARIAMENTE JOSÉ TIROU FÉRIA
-
GABARITO ERRADO
De forma bem simples e direta.
O que é Tautologia - é qdo seus valores são TODOS verdadeiros. ( Então, ele pd ser V ou F? É claro que não.)
O que é Contradição - é qdo seus valores são TODOS Falsos.
O que é Contigência - é qdo seus valores são V e F.
Pronto, vamos para a próxima...
____________________________
O que queremos? Tomar posse.
E quando queremos? É irrelevante.
-
LEIAM COMENTÁRIO Núbia Pattinson
-
Substituindo tudo por F
F^V -> F
F-> F = verdadeiro
Substituindo tudo por V
V^F -> V
F-> V = verdadeiro
GABARITO: ERRADO.
-
GABARITO: ERRADO
Trocando tudo por falso ou por verdadeiro, o resultado será verdadeiro para ambos:
(A∧~C) →B
F^V → F
F → F = verdadeiro
(A∧~C) →B
V^F → V
F→ V = verdadeiro
-
Gente, alguém me socorre?
Eu aprendi aqui pelos comentários do qc que pra ver se é uma tautologia, basta substituir as letras por F e resolver (como vários colegas mostraram nos comentários).
Pois foi o que eu fiz:
(A ^ ~C) --> B
F ^ ~F --> F
F ^ V --> F
F --> F
V
Pensei "é uma tautologia!"
Aí acertei a questão, mas vendo os comentários e fazendo a tabela verdade percebi que NÃO É UMA TAUTOLOGIA.
[A ^ (~C)] → B
V ^ F = F → V = V
V ^ V = V → V = V
V ^ F = F → F = V
V ^ V = V → F = F
F ^ F = F → V = V
F ^ V = F → V = V
F ^ F = F → F = V
F ^ V = F → F = V
Ja entendi o motivo de a questão estar errada (pois dois tiram as férias juntos), o que fiquei sem entender é pq no macete o resultado dá uma tautologia e na tabela verdade não! Fiquei com medo de usar o macete agora!
Alguém sabe explicar isso? Não faz sentido, era para dar a mesma resposta no macete e na tabela verdade!
SOCORROOOO
-
Supergirl concurseira, o segredo está na afirmação do enunciado, onde diz "no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu". No que vc usa essa informação na elaboração da tabela-verdade, acaba achando o gabarito, conforme explicado por comentários abaixo.
Tem muita gente dizendo que acertou a questão usando a estratégia: Coloquei tudo F, depois coloquei tudo V e deu certo. Bom, pra quem fez assim, sinto dizer que acertou na sorte. A questão diz "dependendo de A, B ou C serem verdadeiras ou falsas". Quem fez desse jeito presumiu que as três seriam, ao mesmo tempo, ou verdadeiras ou falsas (ou seja, que A, B e C seriam verdadeiras ou falsas). Macetes são bons, mas é preciso cuidado ao utilizá-los.
Tb vi comentários falando que acertaram por causa do conceito de tautologia, que o enúnciado traz um conceito errado de tautologia. A meu ver, a parte que diz "a proposição não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa", o pronome "ela" faz referência à "proposição". Reescrevendo, ficaria: A proposição não é uma tautologia, isto é, pode ser verdadeira ou falsa, dependendo... Sendo assim, creio ter sido equivocado este pensamento no momento de resolver a questão. Vi que os comentários mais úteis trazem esta ideia, então ficar atento pra isso.
-
DO PROFESSOR DO QC
Lembrando que: “Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu”.
Assim, teremos duas possibilidades, José saiu de férias no mesmo mês com Luís ou com Mário, logo:
1º) Opção.
A: José tirou férias em janeiro de 2013; (V)
B: Luís tirou férias em janeiro de 2013; (V)
C: Mário tirou férias em janeiro de 2013; (F)
(A∧~C) →B – (V ^ ~F) →V = (V ^ V) →V = V→V= V
2ª) Opção.
A: José tirou férias em janeiro de 2013; (V)
B: Luís tirou férias em janeiro de 2013; (F)
C: Mário tirou férias em janeiro de 2013; (V)
(A∧~C) →B – (V ^ ~V) →F = (V ^ F) →F = F→F = V
Assim, é correto afirmar que a proposição (A∧~C) →B é uma tautologia.
Logo a resposta é: Errado.
-
Estranhamente o cometário do Raphael Martins está errado, mas é o mais votado?!
A questão não conceituou tautologia errado, no fim da assertiva ela conceituou o que significa NÃO SER uma tautologia, e conceitua corretamente:
"não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa."
Não ser uma tautologia significa que a proposição pode ser verdadeira ou falsa, dependendo dos valores de A, B ou C.
E ainda erra mais ao montar a tabela verdade e afirmar que "de fato não é uma tautologia", quando é sim uma tautologia!
Apesar de uma das linhas ter o valor de falso, essa linha deve ser desconsiderada, visto que é contraditória com a informação que nos foi dada no enunciado: a de que "no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu."
-
Para quem não entende os comentários sem o gabarito e não tem acesso a resposta.
Gaba: ERRADO
Prezado .L, não estou defendendo se o cara ta errado ou certo, o mais importante aqui é passar o conhecimento e a forma que alguem conseguiu resolver a questão, vc teve sua forma de interpretar e esta certa, o brother que teve a maior pontuação tb teve uma interpretação q deu certo, o legal é contribuir para a galera que esta começando ou tentando enteder e colocar o comentário para ajudar a exclarecer a dúvida e não para gerar duvida no comentário do outro.
a questão apenas perguntou: "... é correto afirmar que a proposição (A∧~C) →B não é uma tautologia"
-
hahaha, Eu tô tão no automático fazendo as tabelas da verdade, que acabei esquecendo das proposições anteriores dadas pelo enunciado. Fiz a tabela, a 4 deu falsa e marquei certo! Ainda pensei, poxa, foi rápido... Nada disso!! HAHA, boa sorte aos colegas de estudo e ATENÇÃAAAO!!!!!! Não façam como a colega aqui..
-
Pode ser até errado fazer assim, mas de cada 10 questões tenho acerto 10.
F ^ ~ F -> F
F ^ v -> F
F -> F
V
-
Resumindo:
Se vc fizer a tabela verdade tomando como base só o comando da questão: não é tautologia.
Se vc fizer a tabela verdade levando em conta a historinha: é tautologia. Pois a linha que dá falso deverá ser desconsiderada.
-
A melhor resposta é do Jonas Silva
, foi muito mais didático
-
Concurseiro Monkey agora consegui entender graças ao seu comentário hahaha.
-
A questão é facil, basta levar em conta que dois sairam de ferias no mesmo mes e em seguida tentar tornar falso a proposição do enunciado (A∧~C) →B. so olhando para o conectivo principal que é o Se... então, ja da pra matar a questão dizendo que É tautologia pois o enunciado diz que 2 saem de ferias em janeiro entao terei que validar como VERDADEIRO duas proposições simples e aí aplicamos a regra da VERA FISCHER para tentar igualar a FALSO a proposicao (A∧~C) →B. mas aqui que está a ultima dica. pois estou tentando igualar a proposicao a FALSO entao terei que considerar que (B é Falso) logo tendo que validar como verdade as proposições A e C, porem a proposição C esta em forma de negação o qual me obriga a deixa-la como FALSA também, logo teríamos: (A -Verdadeiro ∧~C Falso ) →B Falso) = F →F = V
Eis o erro de eu nao conseguir tornar esta proposição FALSA, logo se não consigo torna-la falsa ela é uma TAUTOLOGIA.
A QUESTÃO DIZ QUE NÃO É TAUTOLOGIA= GABARITO ERRADO.
-
Lembrando que: “Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu”.
Assim, teremos duas possibilidades, José saiu de férias no mesmo mês com Luís oucom Mário, logo:
1º) Opção.
A: José tirou férias em janeiro de 2013; (V)
B: Luís tirou férias em janeiro de 2013; (V)
C: Mário tirou férias em janeiro de 2013; (F)
(A∧~C) →B – (V ^ ~F) →V = (V ^ V) →V = V→V= V
2ª) Opção.
A: José tirou férias em janeiro de 2013; (V)
B: Luís tirou férias em janeiro de 2013; (F)
C: Mário tirou férias em janeiro de 2013; (V)
(A∧~C) →B – (V ^ ~V) →F = (V ^ F) →F = F→F = V
Assim, é correto afirmar que a proposição (A∧~C) →B é uma tautologia.
Logo a resposta é: Errado.
Autor:Vinícius Werneck, Matemático, MSc. e PhD Student em Geofísica., de Raciocínio Lógico, Matemática, Matemática Financeira, Não definido
-
TAUTOLOGIA TEM SOMENTE UM ÚNICO VALOR LÓGICO.
NO CASO, V.
-
ERRADO
REALMENTE UMA TAUTOLOGIA É QUANDO UMA PROPOSIÇÃO COMPOSTA É SEMPRE VERDADEIRA,
INDEPENDE DOS VALORES LÓGICOS DAS PROPOSIÇÕES SIMPLES QUE A COMPÕE.
MAS NO CASO DA QUESTÃO NÃO É UMA TAUTOLOGIA, VEJA COMO FICA:
V
V
V
F
V
V
V
V
ASSIM, O CESPE TIRA O FOCO DA TABELA E FAZ VOCÊ ERRAR POR ACHAR QUE O CONCEITO ESTÁ ERRADO.
-
que pegadinha em ?
-
Cuidado pessoal, tem muita resposta errada com muitas curtidas.
A questão está errada devido à afirmação do enunciado: "Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu."
Com esta condição, a linha da tabela verdade de (A∧~C) →B igual à 0 é eliminada.
Então, considerando-se as restrições do enunciado, se trata sim de uma tautologia.
"a proposição (A∧~C) →B NÃO é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa." Tem muita gente que "acertou" a questão "errando" (não leram com atenção a esta frase, que está correta)
-
1 - Questão afirma que não e uma TAUTOLOGIA
Errado ! - Usando o Método Conclusão Falsa você consegue resolver
Conclusão F ou V Ambos deram Verdadeiras
-
Porque devo assumir que quando a questão dfiz "no ano passado" ela está se referindo a 2013? O candidato deve extrapolar a questão para considerar a data em que está fazendo a prova? Estranho, no mínimo.
-
TAUTOLOGIA SEMPRE SERÁ V
-
ERRADO.
A questão necessariamente traz uma tautologia....
pois em P->Q, basta que P seja F para que a sentença fique verdadeira. pois só ocorrerá valor f se V->F [macete só da F quando aparece VERA FISHER]; ENTREEEETANNNNTO...... A questão afirma que " no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu."
“A: José tirou férias em janeiro de 2013”;
“B: Luís tirou férias em janeiro de 2013”; e
“C: Mário tirou férias em janeiro de 2013”
a hipótese que falseava a tautologia era
A = V
B=F
C= F
Ou seja: a hipótese que falseava a tautologia não poderá ser válida pois existe a condição de existência de que LUÍS ou MÁRIO (necessariamente tiraram fériam em Janeiro de 2013!); Portanto É UMA TAUTOLOGIA, independente do valo de A, B ou C, (desde que "B" e "C" não seja ao mesmo tempo Falsos quando A for verdadeiro)....
Questão esquisitíssima.
-
Questão excelente.
Fazendo a tabela verdade encontramos 1 hipótese FALSA, porém, no contexto, ela não é válida.
O enunciado da questão diz que no mesmo mês em que José (A) saiu de férias, ou Luís (B) ou Mário (C) também saíram. Logo, a linha em que temos José com valor VERDADEIRO, Luís e Mario com valor FALSO não deve ser considerada.
Com essa eliminação, temos mesmo uma tautologia.
-
NÃO MONTE A TABELA DO JEITO COMUM, FAÇA NORMALMENTE AS COLUNAS DO A E DO B E NA DO C AO INVÉS DE SEGUIR NORMAL, ATRIBUA VALORES CONTRÁRIOS AOS DO B.
Faça o teste e seja feliz, o porquê tá aí em baixo.
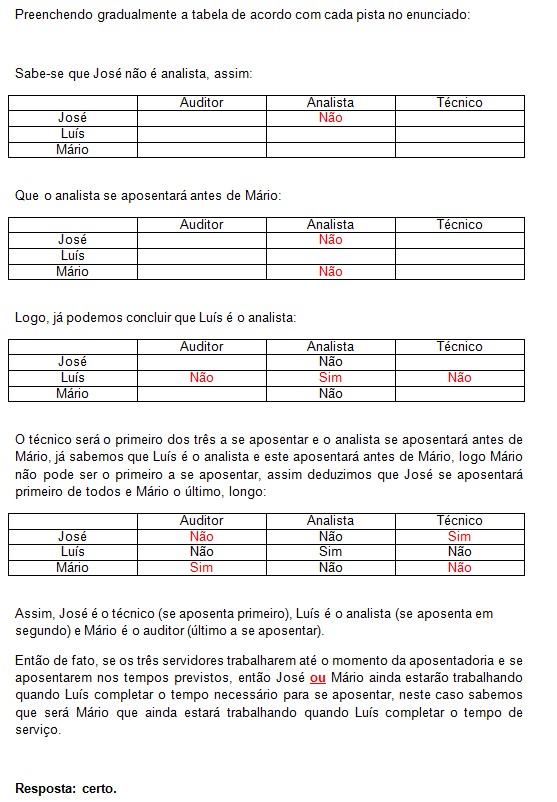
José, Luís e Mário são funcionários públicos nas funções de auditor, analista e técnico, não necessariamente nessa ordem. Sabe-se que José não é analista, que o técnico será o primeiro dos três a se aposentar e que o analista se aposentará antes de Mário. Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu.
Com base nessas informações, julgue os itens que se seguem.
Considerando-se as proposições “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”, é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa.
Atenção ao destaque em azul logo no enunciado, isso quer dizer que, o B e o C não podem tirar férias ao mesmo tempo, B e C são opostos - ou tira férias um ou tira férias o outro, ao mesmo tempo que o A - ou seja quando um for V o outro será F, sempre!
Dessa forma montaremos a tabela normalmente para o A e B enquanto o C assumirá simplesmente o valor contrário do B, já que o valor de um, automaticamente, implica o contrário para o outro. Assim:
A B C (A∧~C) → B = RESULTADO TUDO VERDADEIRO, NÃO TEM O V F = TAUTOLOGIA
V V F V V V
V V F V V V
V F V F F V
V F V F F V
F V F F V V
F V F F V V
F F V F F V
F F V F F V
Logo a questão erra ao dizer que: "(A∧~C) →B não é uma tautologia"
Gabarito: Errado
-
Errado
Apesar de ter acertado, essa questão é uma pegadinha...tem que ler até o fim!
#VemANP
-
boa questão. Não tinha feito nenhuma nesse entendimento ainda.
a tabela realmente não é tautologia, mas o conceito de como é a conclusão do item invalidou a questão.
-
A tabela em si não é tautologia, mas a partir dessa frase "no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu" torna-se uma tautologia.
-
vishi!!!!!!!!!!!!!!!!!!!!
-
Substituindo tudo por F
F^V -> F
F-> F = V (verdadeiro)
Substituindo tudo por V
V^F -> V
F-> V = V (verdadeiro)
GABARITO: ERRADO.
-
Independente
-
Tautologia sempre deve ter o valor verdadeiro, pois se ela puder ter o valor F ou V então é contingência.
-
Ah pronto. Fiz a tabela e na quarta linha o resultado foi F, logo, não é uma tautologia. Como solucionar o comando?